新人教版九年级下数学27.3位似课件
文档属性
| 名称 | 新人教版九年级下数学27.3位似课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-15 16:29:18 | ||
图片预览




文档简介
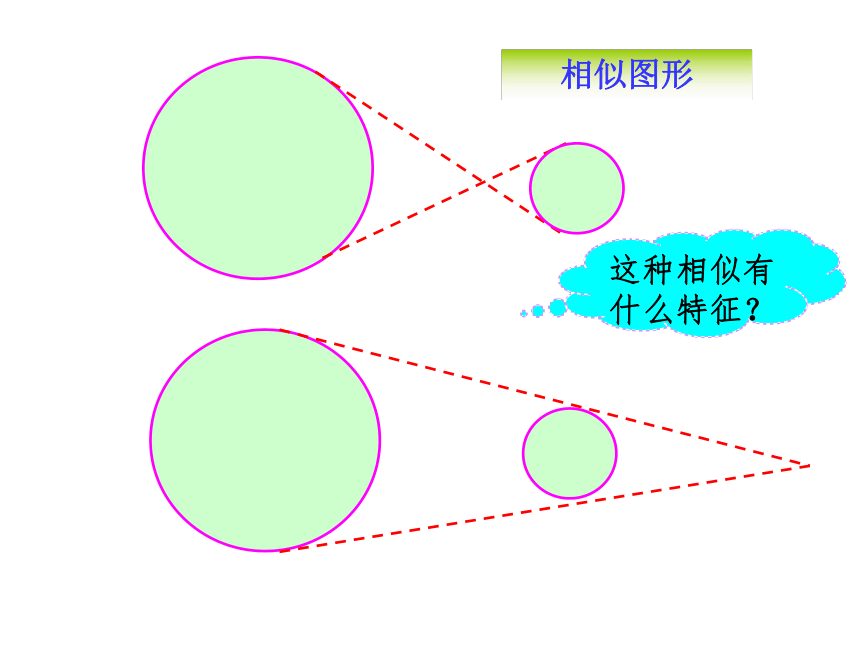
课件37张PPT。新课导入相似图形这种相似有什么特征?相似图形这种相似有什么特征?在幻灯机放映图片的过程中,这些图片有
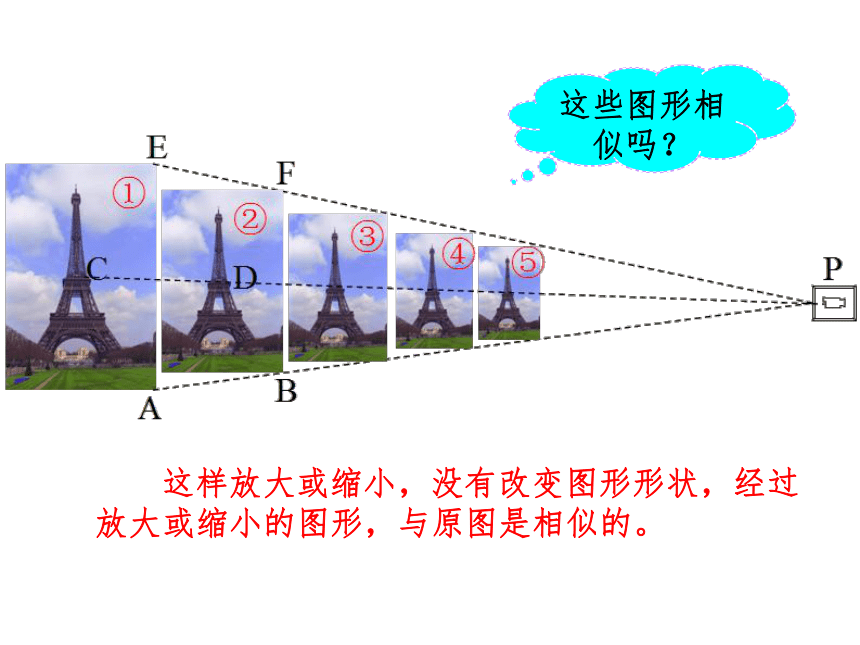
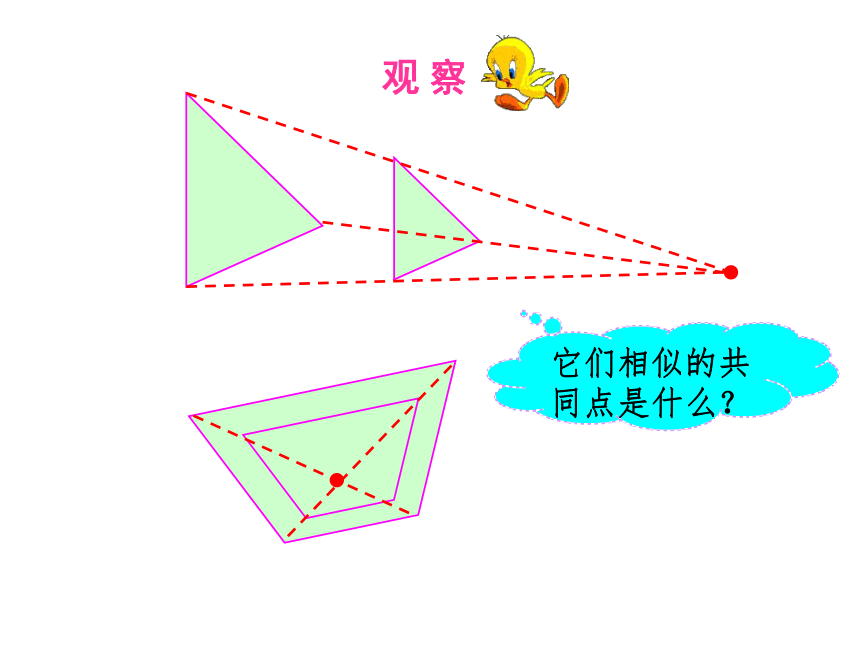
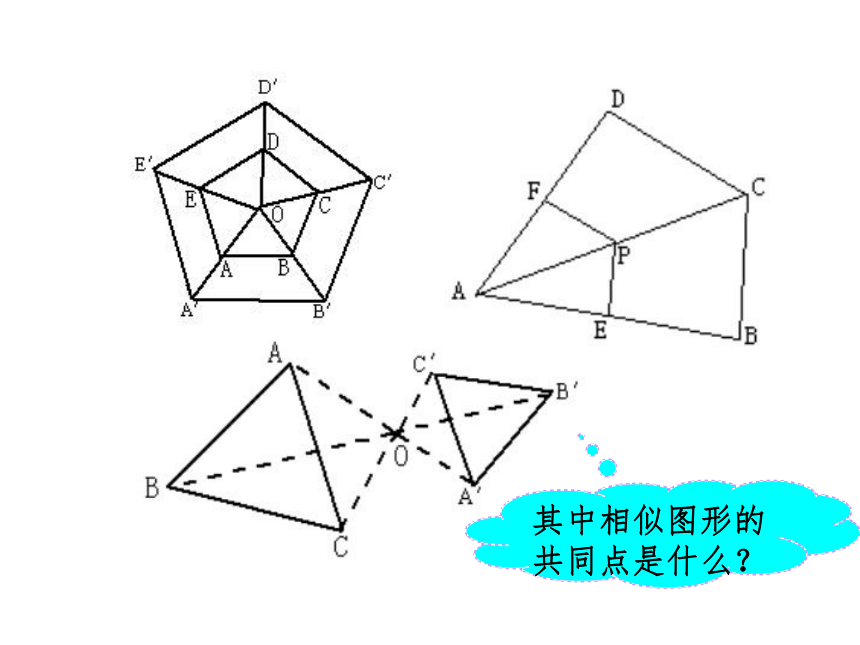
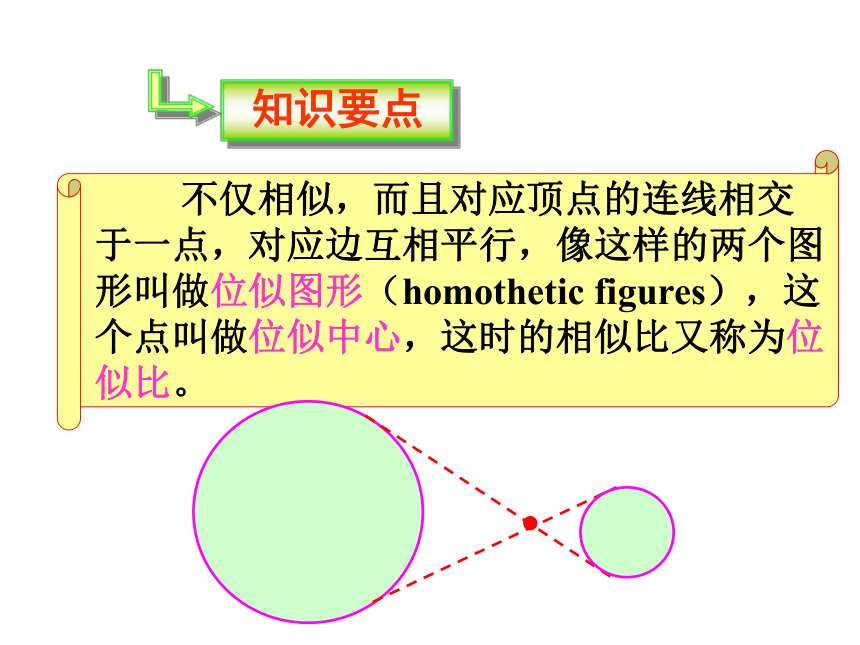
什么关系?2. 幻灯机在哪儿呢?3.我们能给这种有特殊位置的相似图形一个名称吗? 这样放大或缩小,没有改变图形形状,经过放大或缩小的图形,与原图是相似的。这些图形相似吗?观 察它们相似的共同点是什么?其中相似图形的共同点是什么? 不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫做位似图形(homothetic figures),这个点叫做位似中心,这时的相似比又称为位似比。位似图形 位似是一种具有位置关系的相似。
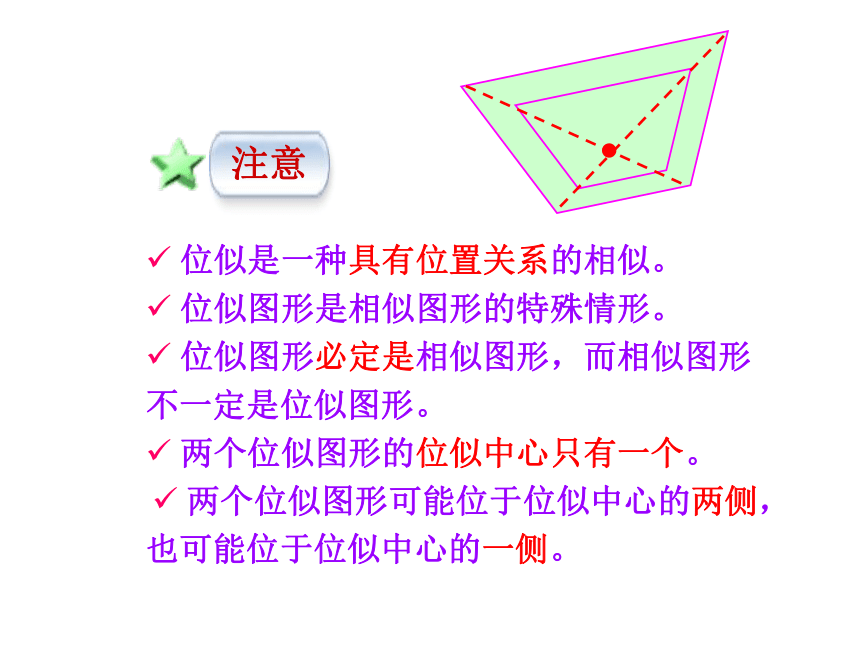
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。注意 对应点与位似中心共线。
位似图形上任意一对应点到位似中心的距离之比等于位似比。位似图形的性质 位似的作用 位似可以将一个图形放大或缩小。 请以坐标原点O为位似中心,作□ ABCD的位似图形,并把它的边长放大3倍。小练习 分析:根据位似图形上任意一对对应点到位似中心的距离之比等于位似比,我们只要连结位似中心O和□ ABCD的各顶点,并把线段延长(或反向延长)到原来的3倍,就得到所求作图形的各个顶点。1. 连结OA,OB,OC,OD.2. 分别延长OA,OB,OC,OD至G,C,E,F,使3. 依次连结GC,CE,EF,FG.四边形GCEF就是所求作的四边形.
如果反向延长OA,OB,OC,OD,就得到四边形G’C’E’F’,也是所求作的四边形.作法: ①确定位似中心,位似中心的位置可随意选择;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形。 位似变换的步骤 小练习 如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比。 位似多边形ABCDEB1A1C1D1E1 在平面直角坐标系中,有两点A(6,3),B(6,0)。以原点O为位似中心,相似比为 ,把线段AB缩小。观察对应点之间坐标的变化,你有什么发现? △ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现? 对称
平移
旋转
相似 图形变换轴对称中心对称平移旋转相似课堂小结1. 位似图形、位似中心、位似比: 如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形。
这个点叫做位似中心。
这时的相似比又称为位似比. 画出基本图形。
选取位似中心。
根据条件确定对应点,并描出对应点。
顺次连结各对应点,所成的图形就是所求的图形。3. 位似图形的画法:随堂练习1. 判断下列各对图形哪些是位似图形,哪些不是. (1)五边形ABCDE与五边形A′B′C′D′E′ (2)正方形ABCD与正方A′B′C′D′√×(3)等边三角形ABC与等边三角形A′B′C′√ 2. 下面的说法对吗?为什么?
(1)分别在△ABC的边AB,AC上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形。
(2)分别在△ABC的边AB,AC的延长线上取点D,E,使DE∥BC,那么△ADE是△ABC放大后的图形。
(3)分别在△ABC的边AB,AC的反向延长线上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形。√×√ 3.如图P,E,F分别是AC,AB,AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比. 是位似图形。
位似中心是点A,
位似比是1:2。 4. 哪些图形是位似图形并指出位似图形的位似中心。√×√位似中心是点O。位似中心是点P。 5. 作出一个新图形,使新图形与原图形对应线段的比是2∶1。 6. (1)如果在射线OA,OB,OC上分别取D,E,F,使OD=2OA, OE=2OB, OF=2OC,那么,结果会怎样? 结果会得到一个放大了的△DEF,且△DEF的三边是△ABC三边的2倍.即它们的位似比是2∶1。 (2)如果在射线AO,BO,CO上分别取点D,E,F使DO=OA,EO=OB,FO=OC,那么,结果又会怎样? 结果会得到一个与△ABC全等的△DEF,.即它们的位似比是1∶1。O 7. 任意画一个三角形,将△ABC的三边缩小为原来的一半。 8. 如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长缩小到原来的一半。
什么关系?2. 幻灯机在哪儿呢?3.我们能给这种有特殊位置的相似图形一个名称吗? 这样放大或缩小,没有改变图形形状,经过放大或缩小的图形,与原图是相似的。这些图形相似吗?观 察它们相似的共同点是什么?其中相似图形的共同点是什么? 不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫做位似图形(homothetic figures),这个点叫做位似中心,这时的相似比又称为位似比。位似图形 位似是一种具有位置关系的相似。
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。注意 对应点与位似中心共线。
位似图形上任意一对应点到位似中心的距离之比等于位似比。位似图形的性质 位似的作用 位似可以将一个图形放大或缩小。 请以坐标原点O为位似中心,作□ ABCD的位似图形,并把它的边长放大3倍。小练习 分析:根据位似图形上任意一对对应点到位似中心的距离之比等于位似比,我们只要连结位似中心O和□ ABCD的各顶点,并把线段延长(或反向延长)到原来的3倍,就得到所求作图形的各个顶点。1. 连结OA,OB,OC,OD.2. 分别延长OA,OB,OC,OD至G,C,E,F,使3. 依次连结GC,CE,EF,FG.四边形GCEF就是所求作的四边形.
如果反向延长OA,OB,OC,OD,就得到四边形G’C’E’F’,也是所求作的四边形.作法: ①确定位似中心,位似中心的位置可随意选择;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形。 位似变换的步骤 小练习 如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比。 位似多边形ABCDEB1A1C1D1E1 在平面直角坐标系中,有两点A(6,3),B(6,0)。以原点O为位似中心,相似比为 ,把线段AB缩小。观察对应点之间坐标的变化,你有什么发现? △ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现? 对称
平移
旋转
相似 图形变换轴对称中心对称平移旋转相似课堂小结1. 位似图形、位似中心、位似比: 如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形。
这个点叫做位似中心。
这时的相似比又称为位似比. 画出基本图形。
选取位似中心。
根据条件确定对应点,并描出对应点。
顺次连结各对应点,所成的图形就是所求的图形。3. 位似图形的画法:随堂练习1. 判断下列各对图形哪些是位似图形,哪些不是. (1)五边形ABCDE与五边形A′B′C′D′E′ (2)正方形ABCD与正方A′B′C′D′√×(3)等边三角形ABC与等边三角形A′B′C′√ 2. 下面的说法对吗?为什么?
(1)分别在△ABC的边AB,AC上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形。
(2)分别在△ABC的边AB,AC的延长线上取点D,E,使DE∥BC,那么△ADE是△ABC放大后的图形。
(3)分别在△ABC的边AB,AC的反向延长线上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形。√×√ 3.如图P,E,F分别是AC,AB,AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比. 是位似图形。
位似中心是点A,
位似比是1:2。 4. 哪些图形是位似图形并指出位似图形的位似中心。√×√位似中心是点O。位似中心是点P。 5. 作出一个新图形,使新图形与原图形对应线段的比是2∶1。 6. (1)如果在射线OA,OB,OC上分别取D,E,F,使OD=2OA, OE=2OB, OF=2OC,那么,结果会怎样? 结果会得到一个放大了的△DEF,且△DEF的三边是△ABC三边的2倍.即它们的位似比是2∶1。 (2)如果在射线AO,BO,CO上分别取点D,E,F使DO=OA,EO=OB,FO=OC,那么,结果又会怎样? 结果会得到一个与△ABC全等的△DEF,.即它们的位似比是1∶1。O 7. 任意画一个三角形,将△ABC的三边缩小为原来的一半。 8. 如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长缩小到原来的一半。
