2.2圆的对称性(第2课时垂径定理)(教学课件)-九年级数学上册考试满分全攻略同步备课备考系列(苏科版)
文档属性
| 名称 | 2.2圆的对称性(第2课时垂径定理)(教学课件)-九年级数学上册考试满分全攻略同步备课备考系列(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-27 11:39:46 | ||
图片预览









文档简介
(共42张PPT)
九年级苏科版数学上册 第二章 对称图形——圆
第二课时 垂径定理
2.2 圆的对称性
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1. 进一步认识圆,了解圆是轴对称图形.
2.理解垂直于弦的直径的性质和推论,并能应用它解决
一些简单的计算、证明和作图问题. (重点)
3.灵活运用垂径定理解决有关圆的问题. (难点)
情景导入
你知道赵州桥吗 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m.
你能求出赵州桥主桥拱的半径吗?
垂径定理
新知探究
O
O
在纸上画⊙O,把⊙O剪下并折叠,使折痕两旁的部分完全重合,你发现了什么?
可以发现无论我们怎么折,这个折痕总是经过⊙O的.
圆是轴对称图形,过圆心的任意一条直线都是它的对称轴.
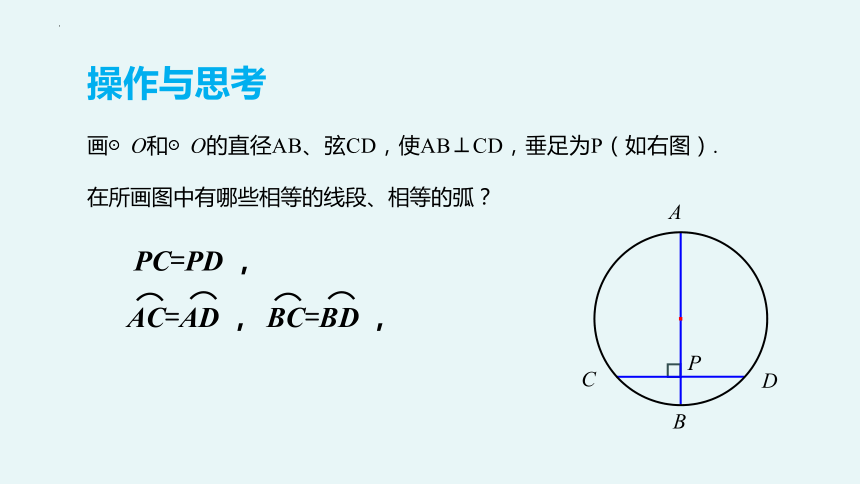
操作与思考
画⊙O和⊙O的直径AB、弦CD,使AB⊥CD,垂足为P(如右图).在所画图中有哪些相等的线段、相等的弧?
·
A
B
P
C
D
PC=PD ,
AC=AD ,
BC=BD ,
︵
︵
︵
︵
P
C
D
A
B
O
P
C
(D)
A
B
O
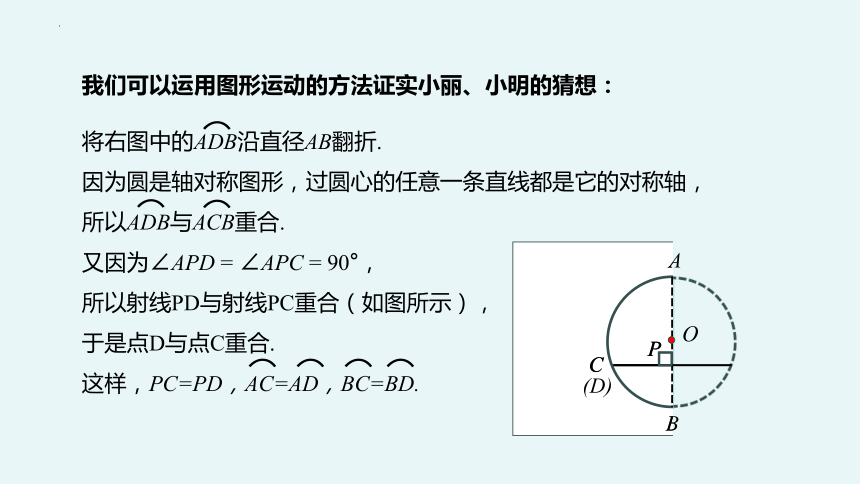
我们可以运用图形运动的方法证实小丽、小明的猜想:
将右图中的ADB沿直径AB翻折.
因为圆是轴对称图形,过圆心的任意一条直线都是它的对称轴,
所以ADB与ACB重合.
又因为∠APD = ∠APC = 90°,
所以射线PD与射线PC重合(如图所示),
于是点D与点C重合.
这样,PC=PD,AC=AD,BC=BD.
︵
︵
︵
︵
︵
︵
︵
连接OC、OD.
如图,AB是⊙O直径,CD是⊙O的弦,AB⊥CD.垂足为P
∴ PC=PD,∠BOC=∠BOD.
在△OCD中,∵OC=OD,OP⊥CD ,
∴ ∠AOC=∠AOD.
(同圆中,相等的圆心角所对的弧相等).
以上结论还可以用下面的方法加以证实:
∴ BC =BD,
AC =AD.
︵
︵
︵
︵
·
O
C
D
A
B
P
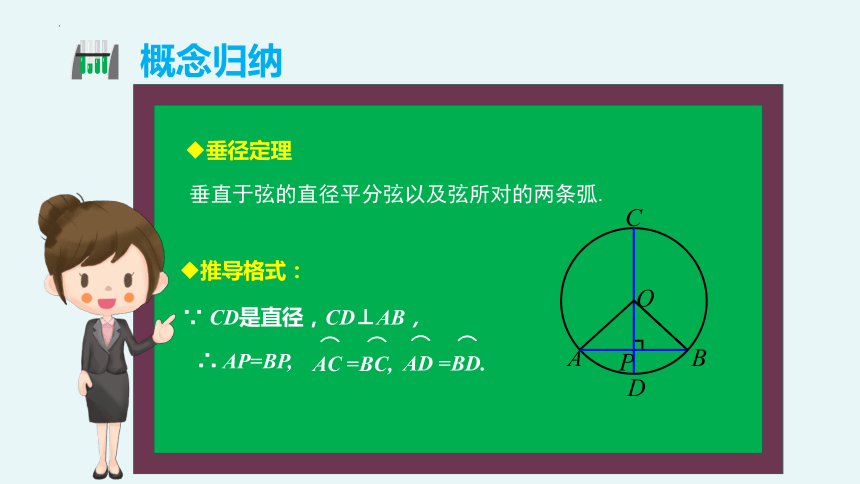
概念归纳
垂径定理
·
O
A
B
C
D
P
垂直于弦的直径平分弦以及弦所对的两条弧.
∵ CD是直径,CD⊥AB,
∴ AP=BP,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
推导格式:
概念归纳
1.“垂直于弦的直径”中的“直径”还可以是垂直于弦的半径或过圆心垂直于弦的直线.
其实质是:过圆心且垂直于弦的线段或直线.
2.“两条弧”是指弦所对的劣弧和优弧或两个半圆.
课本例题
例1. 如图,☉O中,以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D.AC与BD相等吗?为什么?
AC=BD
过点O作OP⊥AB于P.
∵ OP⊥AB,
∴ AP=BP ,CP=DP
(垂直于弦的直径平分弦).
∴ AP-CP=BP-DP,
即 AC=BD.
P
你还有其他解题方法吗?
例1. 如图,☉O中,以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D. AC与BD相等吗?为什么?
AC=BD
连接OA、OC、OD、OB.
∵ OA=OB,OC=OD,
∴∠A=∠B,∠OCD=∠ODC.
∴∠AOC=∠BOD.
∴△AOC≌△BOD.
∴AC=BD.
课本例题
拓展与延伸
如图,AB、CD是⊙O的两条弦,AB∥CD.
试问:AC与BD相等吗?为什么?
⌒
⌒
∵ AB∥CD ,OE⊥AB,
解:AC= BD.
过点O作OE⊥AB于E,并延长交弦CD、⊙O 于F、G.
∴ OF⊥CD.
∴
AG=BG,
CG=DG.
∴AC=BD.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
E
F
G
1.下列图形是否具备垂径定理的条件?
如果不是,请说明为什么?
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
练一练
概念归纳
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
概念归纳
对于圆中的一条直线,如果具备下列五个条件中的任意两个,那么一定具备其他三个:
(1)过圆心; (2)垂直于弦; (3)平分弦(非直径);
(4)平分弦所对的劣弧;
(5)平分弦所对的优弧. 简记为“知二推三”.
你知道为什么要强调非直径吗?
·
O
A
B
D
C
P
1.已知:在☉O中,CD是直径,AB是弦(不是直径),与CD交于点P,且P是AB的中点.
求证:AB⊥CD,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
证明:连接OA、OB、CA、CB,则OA=OB.
即△AOB是等腰三角形.
∵P是AB的中点,
∴AB⊥CD.
即AP=BP,
∵ CD是直径,CD⊥AB,
∴
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
(垂径定理)
练一练
典例剖析
例2.[中考·甘孜州] 如下图,AB是⊙O的直径,弦CD⊥ AB 于点H. 若AB=10,CD=8,则OH 的长度为_________.
3
分析:紧扣垂径定理得到CH=4,再利用勾股定理计算出OH 的长度.
解:如图,连接OC.
∵ CD⊥AB,∴ CH=DH=CD=×8=4(垂直于弦的直径平分弦).
又∵ OC=AB=×10=5,∴在Rt△OCH中,利用勾股定理,得
OH===3.
概念归纳
利用垂径定理求线段的长的方法:
垂径定理是解决圆中的计算、证明问题常用的知识, 求线段长时,一般利用半径、圆心到弦的垂线段、弦的一半构造直角三角形,运用勾股定理求解,即用“垂径定理+勾股定理”求解.
典例剖析
例3.赵州桥(如图)是我国隋代建造的石拱桥,距今约有1 400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37 m,拱高(弧的中点到弦的距离)为7.23 m,求赵州桥主桥拱的半径(结果保留小数点后一位).
回到导入的问题
分析:解决此问题的关键是根据赵州桥的实物图画出几何图形.
解:
如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
(
(
在Rt△OAD中,由勾股定理,得OA2=AD2+OD2,
即R2=18.52+(R-7.23)2. 解得R≈27.3.
因此,赵州桥的主桥拱半径约为27.3 m.
经过圆心O作弦AB的垂线OC,D为垂足,OC与AB相交于点C,
(
连接OA,根据垂径定理,得D是AB的中点,C是AB的中点,CD就是拱高.
(
由题设可知AB=37,CD=7.23,
所以 AD= AB= 37=18.5,OD=OC-CD=R-7.23.
典例剖析
概念归纳
涉及垂径定理时辅助线的添加方法
O
A
B
C
·
在圆中有关弦长a,半径r,弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
概念归纳
弦a,弦心距d,弓形高h,半径r之间有以下关系:
弓形中重要数量关系
d+h=r
A
B
C
D
O
h
r
d
C
随堂练
C
5
随堂练
随堂练
分层练习-基础
1.如图,已知⊙O的直径AB⊥CD于点E,则下列结论错误的是( )
A.CE=DE B.AE=OE
C.BC=BD D.△OCE≌△ODE
B
︵
︵
2. [2023盐城一模]如图,⊙O的半径为5,弦AB=8,OC⊥AB于点C,则OC的长为( )
C
A. 1 B.2 C.3 D.4
分层练习-基础
3.[2023宜昌]如图,OA,OB,OC都是⊙O的半径,AC,OB交于点D.
若AD=CD=8,OD=6,则BD的长为( )
A. 5
B.4
C.3
D.2
B
4.
分层练习-基础
A
分层练习-基础
5.如图,将半径为2的圆形纸片折叠后,圆弧恰好经过
圆心O,则折痕AB的长为________.
6.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧.如图,筒车盛水桶的运行轨道是以轴心O为圆心的圆,水深CD为16 dm,水面宽度AB为48 dm,求轨道的直径.
分层练习-基础
分层练习-巩固
7.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,
连接EB.若AB=4,CD=1,则EB的长为( )
A. 2
B.3
C. 4
D.5
B
分层练习-巩固
8.[2023陕西]陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”(图①)的形状示意图.AB是⊙O的一部分,D是AB的中点,连接 OD,与弦AB交于点C,连接OA,OB.已知AB=24 cm,碗深CD=8 cm,则⊙O的半径OA为( )
A.13 cm B.16 cm
C.17 cm D.26 cm
A
︵
︵
分层练习-巩固
9.如图所示,小区内有个圆形花坛O,点C在弦AB上, AC=11 m,BC=21 m,OC=13 m,则这个花坛的半径为________.
20 m
10.[2024宿迁九年级统考期中]如图,在平面直角坐标系xOy中,以原点O为圆心,13为半径画圆,直线y=kx+3k+4(k≠0)与⊙O交于B,C两点,则弦BC长的最小值为________.
24
分层练习-巩固
11.如图,⊙P的半径为5,弦AB=6,以AB为边作正方形ABCD(点D,P在直线AB两侧).若正方形ABCD绕点P旋转一周,则边CD扫过的面积为________.
9π
分层练习-巩固
12.如图,AB是⊙O的弦,半径OD⊥AB,垂足为H,BC⊥AB,交AD的延长线于点C.
(1)求证:D是AC的中点;
证明:连接BD.
∵AB是⊙O的弦,半径OD⊥AB,
∴D是AB的中点.
∴AD=BD.∴AD=BD.∴∠BAD=∠ABD.
∵BC⊥AB,∴∠ABC=90°.
∴∠BAD+∠C=90°,∠ABD+∠DBC=90°.
︵
︵
︵
∴∠C=∠DBC.∴BD=CD.
∴AD=CD,即D为AC的中点.
分层练习-巩固
13.如图,某地有一座圆弧形的拱桥,桥下的水面宽度为7.2 m,拱顶高出水面2.4 m,现有一艘宽3 m,船舱顶部为长方形并高出水面2 m的货船要经过这里,问:此货船能顺利通过这座拱桥吗?
分层练习-拓展
课堂反馈
两条弧
不是直径
垂直
两条弧
A
课堂反馈
课堂小结
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”).
垂直于弦的直径平分弦以及弦所对的两条弧.
两条辅助线:
连半径,作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
九年级苏科版数学上册 第二章 对称图形——圆
第二课时 垂径定理
2.2 圆的对称性
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1. 进一步认识圆,了解圆是轴对称图形.
2.理解垂直于弦的直径的性质和推论,并能应用它解决
一些简单的计算、证明和作图问题. (重点)
3.灵活运用垂径定理解决有关圆的问题. (难点)
情景导入
你知道赵州桥吗 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m.
你能求出赵州桥主桥拱的半径吗?
垂径定理
新知探究
O
O
在纸上画⊙O,把⊙O剪下并折叠,使折痕两旁的部分完全重合,你发现了什么?
可以发现无论我们怎么折,这个折痕总是经过⊙O的.
圆是轴对称图形,过圆心的任意一条直线都是它的对称轴.
操作与思考
画⊙O和⊙O的直径AB、弦CD,使AB⊥CD,垂足为P(如右图).在所画图中有哪些相等的线段、相等的弧?
·
A
B
P
C
D
PC=PD ,
AC=AD ,
BC=BD ,
︵
︵
︵
︵
P
C
D
A
B
O
P
C
(D)
A
B
O
我们可以运用图形运动的方法证实小丽、小明的猜想:
将右图中的ADB沿直径AB翻折.
因为圆是轴对称图形,过圆心的任意一条直线都是它的对称轴,
所以ADB与ACB重合.
又因为∠APD = ∠APC = 90°,
所以射线PD与射线PC重合(如图所示),
于是点D与点C重合.
这样,PC=PD,AC=AD,BC=BD.
︵
︵
︵
︵
︵
︵
︵
连接OC、OD.
如图,AB是⊙O直径,CD是⊙O的弦,AB⊥CD.垂足为P
∴ PC=PD,∠BOC=∠BOD.
在△OCD中,∵OC=OD,OP⊥CD ,
∴ ∠AOC=∠AOD.
(同圆中,相等的圆心角所对的弧相等).
以上结论还可以用下面的方法加以证实:
∴ BC =BD,
AC =AD.
︵
︵
︵
︵
·
O
C
D
A
B
P
概念归纳
垂径定理
·
O
A
B
C
D
P
垂直于弦的直径平分弦以及弦所对的两条弧.
∵ CD是直径,CD⊥AB,
∴ AP=BP,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
推导格式:
概念归纳
1.“垂直于弦的直径”中的“直径”还可以是垂直于弦的半径或过圆心垂直于弦的直线.
其实质是:过圆心且垂直于弦的线段或直线.
2.“两条弧”是指弦所对的劣弧和优弧或两个半圆.
课本例题
例1. 如图,☉O中,以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D.AC与BD相等吗?为什么?
AC=BD
过点O作OP⊥AB于P.
∵ OP⊥AB,
∴ AP=BP ,CP=DP
(垂直于弦的直径平分弦).
∴ AP-CP=BP-DP,
即 AC=BD.
P
你还有其他解题方法吗?
例1. 如图,☉O中,以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D. AC与BD相等吗?为什么?
AC=BD
连接OA、OC、OD、OB.
∵ OA=OB,OC=OD,
∴∠A=∠B,∠OCD=∠ODC.
∴∠AOC=∠BOD.
∴△AOC≌△BOD.
∴AC=BD.
课本例题
拓展与延伸
如图,AB、CD是⊙O的两条弦,AB∥CD.
试问:AC与BD相等吗?为什么?
⌒
⌒
∵ AB∥CD ,OE⊥AB,
解:AC= BD.
过点O作OE⊥AB于E,并延长交弦CD、⊙O 于F、G.
∴ OF⊥CD.
∴
AG=BG,
CG=DG.
∴AC=BD.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
E
F
G
1.下列图形是否具备垂径定理的条件?
如果不是,请说明为什么?
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
练一练
概念归纳
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
概念归纳
对于圆中的一条直线,如果具备下列五个条件中的任意两个,那么一定具备其他三个:
(1)过圆心; (2)垂直于弦; (3)平分弦(非直径);
(4)平分弦所对的劣弧;
(5)平分弦所对的优弧. 简记为“知二推三”.
你知道为什么要强调非直径吗?
·
O
A
B
D
C
P
1.已知:在☉O中,CD是直径,AB是弦(不是直径),与CD交于点P,且P是AB的中点.
求证:AB⊥CD,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
证明:连接OA、OB、CA、CB,则OA=OB.
即△AOB是等腰三角形.
∵P是AB的中点,
∴AB⊥CD.
即AP=BP,
∵ CD是直径,CD⊥AB,
∴
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
(垂径定理)
练一练
典例剖析
例2.[中考·甘孜州] 如下图,AB是⊙O的直径,弦CD⊥ AB 于点H. 若AB=10,CD=8,则OH 的长度为_________.
3
分析:紧扣垂径定理得到CH=4,再利用勾股定理计算出OH 的长度.
解:如图,连接OC.
∵ CD⊥AB,∴ CH=DH=CD=×8=4(垂直于弦的直径平分弦).
又∵ OC=AB=×10=5,∴在Rt△OCH中,利用勾股定理,得
OH===3.
概念归纳
利用垂径定理求线段的长的方法:
垂径定理是解决圆中的计算、证明问题常用的知识, 求线段长时,一般利用半径、圆心到弦的垂线段、弦的一半构造直角三角形,运用勾股定理求解,即用“垂径定理+勾股定理”求解.
典例剖析
例3.赵州桥(如图)是我国隋代建造的石拱桥,距今约有1 400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37 m,拱高(弧的中点到弦的距离)为7.23 m,求赵州桥主桥拱的半径(结果保留小数点后一位).
回到导入的问题
分析:解决此问题的关键是根据赵州桥的实物图画出几何图形.
解:
如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
(
(
在Rt△OAD中,由勾股定理,得OA2=AD2+OD2,
即R2=18.52+(R-7.23)2. 解得R≈27.3.
因此,赵州桥的主桥拱半径约为27.3 m.
经过圆心O作弦AB的垂线OC,D为垂足,OC与AB相交于点C,
(
连接OA,根据垂径定理,得D是AB的中点,C是AB的中点,CD就是拱高.
(
由题设可知AB=37,CD=7.23,
所以 AD= AB= 37=18.5,OD=OC-CD=R-7.23.
典例剖析
概念归纳
涉及垂径定理时辅助线的添加方法
O
A
B
C
·
在圆中有关弦长a,半径r,弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
概念归纳
弦a,弦心距d,弓形高h,半径r之间有以下关系:
弓形中重要数量关系
d+h=r
A
B
C
D
O
h
r
d
C
随堂练
C
5
随堂练
随堂练
分层练习-基础
1.如图,已知⊙O的直径AB⊥CD于点E,则下列结论错误的是( )
A.CE=DE B.AE=OE
C.BC=BD D.△OCE≌△ODE
B
︵
︵
2. [2023盐城一模]如图,⊙O的半径为5,弦AB=8,OC⊥AB于点C,则OC的长为( )
C
A. 1 B.2 C.3 D.4
分层练习-基础
3.[2023宜昌]如图,OA,OB,OC都是⊙O的半径,AC,OB交于点D.
若AD=CD=8,OD=6,则BD的长为( )
A. 5
B.4
C.3
D.2
B
4.
分层练习-基础
A
分层练习-基础
5.如图,将半径为2的圆形纸片折叠后,圆弧恰好经过
圆心O,则折痕AB的长为________.
6.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧.如图,筒车盛水桶的运行轨道是以轴心O为圆心的圆,水深CD为16 dm,水面宽度AB为48 dm,求轨道的直径.
分层练习-基础
分层练习-巩固
7.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,
连接EB.若AB=4,CD=1,则EB的长为( )
A. 2
B.3
C. 4
D.5
B
分层练习-巩固
8.[2023陕西]陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”(图①)的形状示意图.AB是⊙O的一部分,D是AB的中点,连接 OD,与弦AB交于点C,连接OA,OB.已知AB=24 cm,碗深CD=8 cm,则⊙O的半径OA为( )
A.13 cm B.16 cm
C.17 cm D.26 cm
A
︵
︵
分层练习-巩固
9.如图所示,小区内有个圆形花坛O,点C在弦AB上, AC=11 m,BC=21 m,OC=13 m,则这个花坛的半径为________.
20 m
10.[2024宿迁九年级统考期中]如图,在平面直角坐标系xOy中,以原点O为圆心,13为半径画圆,直线y=kx+3k+4(k≠0)与⊙O交于B,C两点,则弦BC长的最小值为________.
24
分层练习-巩固
11.如图,⊙P的半径为5,弦AB=6,以AB为边作正方形ABCD(点D,P在直线AB两侧).若正方形ABCD绕点P旋转一周,则边CD扫过的面积为________.
9π
分层练习-巩固
12.如图,AB是⊙O的弦,半径OD⊥AB,垂足为H,BC⊥AB,交AD的延长线于点C.
(1)求证:D是AC的中点;
证明:连接BD.
∵AB是⊙O的弦,半径OD⊥AB,
∴D是AB的中点.
∴AD=BD.∴AD=BD.∴∠BAD=∠ABD.
∵BC⊥AB,∴∠ABC=90°.
∴∠BAD+∠C=90°,∠ABD+∠DBC=90°.
︵
︵
︵
∴∠C=∠DBC.∴BD=CD.
∴AD=CD,即D为AC的中点.
分层练习-巩固
13.如图,某地有一座圆弧形的拱桥,桥下的水面宽度为7.2 m,拱顶高出水面2.4 m,现有一艘宽3 m,船舱顶部为长方形并高出水面2 m的货船要经过这里,问:此货船能顺利通过这座拱桥吗?
分层练习-拓展
课堂反馈
两条弧
不是直径
垂直
两条弧
A
课堂反馈
课堂小结
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”).
垂直于弦的直径平分弦以及弦所对的两条弧.
两条辅助线:
连半径,作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
