2.3确定圆的条件(教学课件)-九年级数学上册考试满分全攻略同步备课备考系列(苏科版)
文档属性
| 名称 | 2.3确定圆的条件(教学课件)-九年级数学上册考试满分全攻略同步备课备考系列(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-27 11:50:19 | ||
图片预览











文档简介
(共35张PPT)
九年级苏科版数学上册 第二章 对称图形——圆
2.3 确定圆的条件
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.了解不在同一条直线上的三点确定一个圆的探索过程.(重点)
2.了解三角形的外接圆、三角形的外心、圆的内接三角形的概念.(重点、难点)
3.会过不在同一条直线上的三点作一个圆.
情景导入
1.圆是 图形,圆心是它的 ,过圆心的 一条直线都是它的对称轴.
2.在同圆或等圆中,相等的圆心角 相等, 相等.
3.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么 。
4. 与它所对的弧的度数相等.
5.垂径定理:垂直于弦的直径平分 .
中心对称
对称中心
任意
所对的弧
所对的弦
它们所对应的其余各组量都分别相等
圆心角的度数
弦以及弦所对的两条弧
上节课我们学习了圆的对称性,请你回顾所学内容回答下列问题.
情景导入
小明不小心打碎了家里的一块圆形玻璃镜子,现欲重新配制一块玻璃片补上,他准备把碎玻璃片连同这块残片一起拿到玻璃店,这样可以配到吗?
1.确定一个圆的条件
新知探究
1.怎样作一个圆,使它经过已知点A?这样的圆可以作多少个?
● A
在平面内任取一点,以这点为圆心,它到点A的距离为半径作圆.经过点A的圆可以作无数个.
1.怎样作一个圆,使它经过已知点A、B?这样的圆可以作多少个?
A
B
O
●
O
●
O
●
O
●
O
●
以线段AB的垂直平分线上任意一点为圆心,这点到点A的距离为半径作圆.经过点A、B的圆可以作无数个.
概念归纳
3.能否作一个圆,使它经过A,B,C三点?如果能,这样的圆可以作多少个?
经过A、B、C三点作圆,圆心应在线段AB的垂直平分线 l 上,又在线段BC的垂直平分线 l ,上.
l 与l 可能平行,也可能相交.
A
B
C
l
l
1.如果三个点在同一直线时可以作圆吗?为什么?
答:如图,当A,B,C三点在同一条直线上时,因为到A,B两点距离相等的点的集合是线段AB的垂直平分线,到B,C两点距离相等的点的集合是线段BC的垂直平分线,两条直线垂直于同一条直线,所以线段AB的垂直平分线与线段BC的垂直平分线平行,没有交点,故没有一点到A,B,C三点的距离相等,不存在圆心,从而经过同一直线上的三点不能作圆.
A
B
C
2.如果 A,B,C 三点不在同一条直线上.能作圆吗?
B
A
C
能否转化为2的情况:经过两点A,B的圆的圆心在线段AB的垂直平分线上.
你准备如何(确定圆心,半径)作圆?
B
A
C
(1)连结 AB,BC.
(2)分别作线段 AB,BC 的垂直平分线 DE 和 FG,DE 与 FG 相交于点 O.
E
D
F
G
O
(3)以 O 为圆心,以 OB 的长为半径作圆.
⊙O 就是所要求作的圆.
作法步骤
B
A
C
E
D
F
G
O
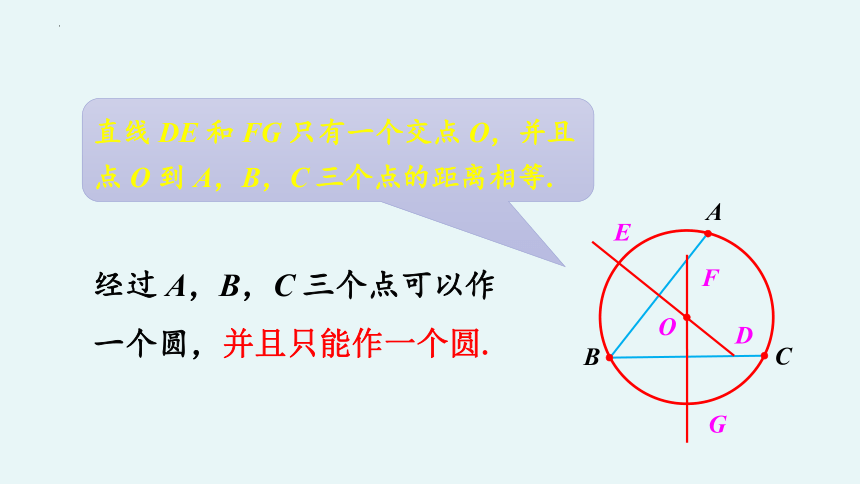
直线 DE 和 FG 只有一个交点 O,并且点 O 到 A,B,C 三个点的距离相等.
经过 A,B,C 三个点可以作一个圆,并且只能作一个圆.
B
A
C
E
D
F
G
O
不在同一直线上的三个点确定一个圆.
三角形的三个顶点确定一个圆,
这个圆叫做三角形的外接圆.
一个三角形有___个外接圆,
而一个圆有_____个内接三角形.
一
无数
B
A
C
O
外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心.
不在同一直线上的三个点确定一个圆.
分别作出锐角三角形、直角三角形、钝角三角形的外接圆,并说明它们外心的位置情况.
B
A
C
O
O
B
A
C
B
A
C
O
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
B
A
随堂练
随堂练
6
随堂练
分层练习-基础
1.一个三角形的外心在它的内部,则这个三角形一定是 ( )
A.钝角三角形 B.直角三角形
C.锐角三角形 D.等边三角形
C
2.[2023江西]如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3个 B.4个
C.5个 D.6个
D
分层练习-基础
D
3.[2021·江苏盐城校级月考]如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是( )
A.(2,3) B. (3,2)
C.(1,3) D. (3,1)
分层练习-基础
4.[2023连云港月考]已知点O是△ABC的外心,且AO+ BO=6,则CO=________.
3
5.[2023淮安清江浦区期中]已知△ABC三边长分别为5, 12,13,则这个三角形的外接圆的半径为_________.
6.5
6.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是________.
(3,1)
分层练习-基础
7.如图,已知直线a和直线外的两点A,B,经过A,B作一圆,使它的圆心在直线a上.(保留作图的痕迹,不写 作法)
解:作图如图所示.
分层练习-巩固
8.如图所示的网格由边长相同的小正方形组成,点A,B,C,D,E,F,G在小正方形的顶点上,
则△ABC的外心是( )
A.点D B.点E
C.点F D.点G
A
分层练习-巩固
9.
D
分层练习-巩固
10.若一个直角三角形的两条边长分别为5和12,则这个三角形的外接圆的直径长为________.
12或13
11.[2024周口九年级统考阶段练习]△ABC的边AB=8,边AC,BC的长是一元二次方程m2-16m+60=0的两 根,则△ABC的外接圆的半径长为________.
5
12.
分层练习-巩固
13.如图,AB=4,C为线段AB上的一个动点(不与点A,B重合),分别以AC,BC为边作等边三角形ACD和等边三角形BCE,则在点C运动的过程中,△CDE的外接圆面积的最小值为________.
14.如图,已知AD既是△ABC的中线,又是角平分线.
(1)判断△ABC的形状,并证明你的结论.
分层练习-巩固
(2)AD是否过△ABC外接圆的圆心O,并证明你的结论.
解:AD过△ABC的外接圆圆心O.
证明:∵AB=AC,AD是角平分线,
∴AD⊥BC.
又∵BD=CD,∴AD是BC的垂直平分线.
∴AD过△ABC外接圆的圆心O.
分层练习-巩固
15.如图①,已知△ABC中,BA=BC,D是平面内不与A,B,C重合的一点,∠ABC=∠DBE,BD=BE,连接AD,CE.
分层练习-拓展
(1)求证:△ABD≌△CBE;
分层练习-拓展
(2)如图②,当点D是△ABC的外接圆圆心时,连接CD.
①请判断四边形BDCE的形状,并证明你的结论.
解:四边形BDCE是菱形.证明如下:
∵∠ABC=∠DBE,
∴∠ABC-∠CBD=∠DBE-∠CBD,
即∠ABD=∠CBE.
分层练习-拓展
②当∠ABC为多少度时,点E在⊙D上?请说明理由.
解:当∠ABC为60°时,点E在⊙D上.
理由如下:
连接DE,当∠ABC为60°时,∠DBE也为60°.
又∵BD=BE,∴△BDE为等边三角形.
∴DE=DB,即点E在⊙D上.
分层练习-拓展
圆心
半径
不在同一条直线上
B
外接圆
三边的垂直平分线
课堂反馈
B
(3,1)
课堂反馈
课堂小结
作圆
过一点可以作无数个圆
过两点可以作无数个圆
不在同一直线上的三个点确定一个圆
注意:同一直线上的三个点不能作圆
三角形外接圆
概念
性质
三角形的外心到三角形的三个顶点的距离相等.
经过三角形的三个顶点的圆叫做三角形的外接圆
外心
外接圆的圆心叫三角形的外心
九年级苏科版数学上册 第二章 对称图形——圆
2.3 确定圆的条件
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.了解不在同一条直线上的三点确定一个圆的探索过程.(重点)
2.了解三角形的外接圆、三角形的外心、圆的内接三角形的概念.(重点、难点)
3.会过不在同一条直线上的三点作一个圆.
情景导入
1.圆是 图形,圆心是它的 ,过圆心的 一条直线都是它的对称轴.
2.在同圆或等圆中,相等的圆心角 相等, 相等.
3.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么 。
4. 与它所对的弧的度数相等.
5.垂径定理:垂直于弦的直径平分 .
中心对称
对称中心
任意
所对的弧
所对的弦
它们所对应的其余各组量都分别相等
圆心角的度数
弦以及弦所对的两条弧
上节课我们学习了圆的对称性,请你回顾所学内容回答下列问题.
情景导入
小明不小心打碎了家里的一块圆形玻璃镜子,现欲重新配制一块玻璃片补上,他准备把碎玻璃片连同这块残片一起拿到玻璃店,这样可以配到吗?
1.确定一个圆的条件
新知探究
1.怎样作一个圆,使它经过已知点A?这样的圆可以作多少个?
● A
在平面内任取一点,以这点为圆心,它到点A的距离为半径作圆.经过点A的圆可以作无数个.
1.怎样作一个圆,使它经过已知点A、B?这样的圆可以作多少个?
A
B
O
●
O
●
O
●
O
●
O
●
以线段AB的垂直平分线上任意一点为圆心,这点到点A的距离为半径作圆.经过点A、B的圆可以作无数个.
概念归纳
3.能否作一个圆,使它经过A,B,C三点?如果能,这样的圆可以作多少个?
经过A、B、C三点作圆,圆心应在线段AB的垂直平分线 l 上,又在线段BC的垂直平分线 l ,上.
l 与l 可能平行,也可能相交.
A
B
C
l
l
1.如果三个点在同一直线时可以作圆吗?为什么?
答:如图,当A,B,C三点在同一条直线上时,因为到A,B两点距离相等的点的集合是线段AB的垂直平分线,到B,C两点距离相等的点的集合是线段BC的垂直平分线,两条直线垂直于同一条直线,所以线段AB的垂直平分线与线段BC的垂直平分线平行,没有交点,故没有一点到A,B,C三点的距离相等,不存在圆心,从而经过同一直线上的三点不能作圆.
A
B
C
2.如果 A,B,C 三点不在同一条直线上.能作圆吗?
B
A
C
能否转化为2的情况:经过两点A,B的圆的圆心在线段AB的垂直平分线上.
你准备如何(确定圆心,半径)作圆?
B
A
C
(1)连结 AB,BC.
(2)分别作线段 AB,BC 的垂直平分线 DE 和 FG,DE 与 FG 相交于点 O.
E
D
F
G
O
(3)以 O 为圆心,以 OB 的长为半径作圆.
⊙O 就是所要求作的圆.
作法步骤
B
A
C
E
D
F
G
O
直线 DE 和 FG 只有一个交点 O,并且点 O 到 A,B,C 三个点的距离相等.
经过 A,B,C 三个点可以作一个圆,并且只能作一个圆.
B
A
C
E
D
F
G
O
不在同一直线上的三个点确定一个圆.
三角形的三个顶点确定一个圆,
这个圆叫做三角形的外接圆.
一个三角形有___个外接圆,
而一个圆有_____个内接三角形.
一
无数
B
A
C
O
外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心.
不在同一直线上的三个点确定一个圆.
分别作出锐角三角形、直角三角形、钝角三角形的外接圆,并说明它们外心的位置情况.
B
A
C
O
O
B
A
C
B
A
C
O
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
B
A
随堂练
随堂练
6
随堂练
分层练习-基础
1.一个三角形的外心在它的内部,则这个三角形一定是 ( )
A.钝角三角形 B.直角三角形
C.锐角三角形 D.等边三角形
C
2.[2023江西]如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3个 B.4个
C.5个 D.6个
D
分层练习-基础
D
3.[2021·江苏盐城校级月考]如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是( )
A.(2,3) B. (3,2)
C.(1,3) D. (3,1)
分层练习-基础
4.[2023连云港月考]已知点O是△ABC的外心,且AO+ BO=6,则CO=________.
3
5.[2023淮安清江浦区期中]已知△ABC三边长分别为5, 12,13,则这个三角形的外接圆的半径为_________.
6.5
6.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是________.
(3,1)
分层练习-基础
7.如图,已知直线a和直线外的两点A,B,经过A,B作一圆,使它的圆心在直线a上.(保留作图的痕迹,不写 作法)
解:作图如图所示.
分层练习-巩固
8.如图所示的网格由边长相同的小正方形组成,点A,B,C,D,E,F,G在小正方形的顶点上,
则△ABC的外心是( )
A.点D B.点E
C.点F D.点G
A
分层练习-巩固
9.
D
分层练习-巩固
10.若一个直角三角形的两条边长分别为5和12,则这个三角形的外接圆的直径长为________.
12或13
11.[2024周口九年级统考阶段练习]△ABC的边AB=8,边AC,BC的长是一元二次方程m2-16m+60=0的两 根,则△ABC的外接圆的半径长为________.
5
12.
分层练习-巩固
13.如图,AB=4,C为线段AB上的一个动点(不与点A,B重合),分别以AC,BC为边作等边三角形ACD和等边三角形BCE,则在点C运动的过程中,△CDE的外接圆面积的最小值为________.
14.如图,已知AD既是△ABC的中线,又是角平分线.
(1)判断△ABC的形状,并证明你的结论.
分层练习-巩固
(2)AD是否过△ABC外接圆的圆心O,并证明你的结论.
解:AD过△ABC的外接圆圆心O.
证明:∵AB=AC,AD是角平分线,
∴AD⊥BC.
又∵BD=CD,∴AD是BC的垂直平分线.
∴AD过△ABC外接圆的圆心O.
分层练习-巩固
15.如图①,已知△ABC中,BA=BC,D是平面内不与A,B,C重合的一点,∠ABC=∠DBE,BD=BE,连接AD,CE.
分层练习-拓展
(1)求证:△ABD≌△CBE;
分层练习-拓展
(2)如图②,当点D是△ABC的外接圆圆心时,连接CD.
①请判断四边形BDCE的形状,并证明你的结论.
解:四边形BDCE是菱形.证明如下:
∵∠ABC=∠DBE,
∴∠ABC-∠CBD=∠DBE-∠CBD,
即∠ABD=∠CBE.
分层练习-拓展
②当∠ABC为多少度时,点E在⊙D上?请说明理由.
解:当∠ABC为60°时,点E在⊙D上.
理由如下:
连接DE,当∠ABC为60°时,∠DBE也为60°.
又∵BD=BE,∴△BDE为等边三角形.
∴DE=DB,即点E在⊙D上.
分层练习-拓展
圆心
半径
不在同一条直线上
B
外接圆
三边的垂直平分线
课堂反馈
B
(3,1)
课堂反馈
课堂小结
作圆
过一点可以作无数个圆
过两点可以作无数个圆
不在同一直线上的三个点确定一个圆
注意:同一直线上的三个点不能作圆
三角形外接圆
概念
性质
三角形的外心到三角形的三个顶点的距离相等.
经过三角形的三个顶点的圆叫做三角形的外接圆
外心
外接圆的圆心叫三角形的外心
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
