2.4线段、角的轴对称性(第1课时线段垂直平分线的性质)(教学课件)-八年级数学上册考试满分全攻略同步备课备考系列(苏科版)
文档属性
| 名称 | 2.4线段、角的轴对称性(第1课时线段垂直平分线的性质)(教学课件)-八年级数学上册考试满分全攻略同步备课备考系列(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-27 11:54:10 | ||
图片预览











文档简介
(共35张PPT)
第一课时 线段垂直平分线的性质
八年级苏科版数学上册 第二章 轴对称与轴对称图形
2.4 线段、角的轴对称性
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.理解线段的垂直平分线的相关概念. (重点)
2.掌握线段垂直平分线的定义. (重点)
3.利用线段的垂直平分线的性质解决问题.
(重点、难点)
情景导入
1.什么样的图形叫作轴对称图形?
把一个图形沿着某条直线对折,如果对折的两部分是完全重合的,我们就称这样的图形为轴对称图形,这条直线叫作这个图形的对称轴.
旧知回顾
这里有一条线段,它是轴对称图形吗?
a
b
l
对称轴l与线段ab之间存在某种关系呢?
某市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等.
情景导入
A
B
C
1.线段的垂直平分线
新知探究
如右图,直线l是线段AB的垂直平分线,l交AB于点O.把OA沿直线l翻折,因为∠1=∠2=90°,OA=OB,所以 OA 与OB 重合.
A
B
l
O
1
2
线段是轴对称图形,线段的垂直平分线是它的对称轴.
垂直于一条线段,并且平分这条线段的直线,叫作这条线段的垂直平分线.
线段的垂直平分线
l
l
思考探究
如下图,线段 AB 的垂直平分线l交 AB 于点 O,点 P 在l上.
PA 与 PB 相等吗?
A
P
B
O
P
B(A)
O
A
B
O
C
A
O
B
P
我们可以运用图形运动的方法,利用线段的轴对称性,证明PA=PB.
(1)在纸片上画一条线段AB,对折AB使点A,B重合;
(2)在折痕上任取一点P,沿PA将纸折叠;
(3)把纸展开,得到折痕PA和PB.
因为∠POA=∠POB,所以OA落在射线OB上.
因为OA=OB,所以点A与点B重合,
依据基本事实“两点确定一条直线”,
可知PA与PB重合,所以PA=PB.
典例剖析
A
B
P
M
N
O
例1.已知:直线MN⊥AB,垂足为O,且AO=OB.点P在MN上.你能得到 PA=PB吗
解:能得到 PA=PB
∵MN⊥AB ∴∠POA=∠POB=90o
在 ΔPOC和Δ POC中,
AO=BO
∠ POA= ∠ POB ;PO=PO
∴ ΔPAO ≌Δ PBO ∴PA=PB
∵ MN⊥AB,AO=OB.点P在MN上.
∴ PA=PB(线段垂直平分线上的点和这条线段两个端点的距离相等)
概念归纳
于是,我们得到如下定理:
线段垂直平分线上的点到线段两端的距离相等
几何语言
如右图,∵点A在线段BC的垂直平分线上,
∴ AB=AC.
易错提醒
线段有两条对称轴,线段的垂直平分线是它的对称轴,线段自身所在的直线也是它的对称轴.
l
B
A
C
D
概念归纳
特别注意:
线段垂直平分线的性质中的“ 距离”是“该点与
这条线段两个端点的距离”.
2. 用线段垂直平分线的性质可直接证明线段相等,
不必再用三角形全等来证明,因此它为证明线段
相等提供了新方法.
如右图,点P在线段AB的垂直平分线l外,PA交l于点Q,连接QB.
因为点Q在AB的垂直平分线上,
所以QA= QB,
于是PA= PQ+ QA =PQ +QB > PB.
例2.线段垂直平分线上外点,到这条线段两端的距离相等吗 为什么
解:不相等;因为到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
B
l
P
Q
●
●
A
课本例题
练一练
1.[月考·江阴] 如图2.4-2,在△ABC中,AB边的垂直平分线DE,分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG,分别与BC边和AC边交于点F和点G,又△BEG的周长为16,且GE=1,
则AC的长为( )
A. 16 B. 15
C. 14 D. 13
C
分析:利用线段垂直平分线的性质进行线段间的转化是一种常用的解题方法.本题中解题的关键是利用线段垂直平分线的性质, 将△BEG的周长转化为线段 AC+2GE的长,最后代入求解.
我们回到导入的问题
某市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等.
B
A
C
p
PA=PB=PC
转化为数学模型
∴购物中心建在P点处与三个小区的距离相等
A
B
C
2.已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
试说明PA=PB=PC吗
解:∵点P在线段AB的垂直平分线MN上,
∴PA=PB(性质定理).
同理 PB=PC.
∴PA=PB=PC.
B
A
C
M
N
P
M'
N'
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
练一练
归纳总结
1.垂直于一条线段,并且平分这条线段的直线,叫作
这条线段的垂直平分线.
线段的垂直平分线
2.线段垂直平分线的性质:
线段垂直平分线上的点
到这条线段两个端点的
距离相等.
3 线段的对称轴是这条线段的垂直平分线.
A
B
O
1.如图,直线CD是线段PB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
P
A
B
C
D
B
随堂练
2.如图,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
10cm
A
B
C
D
E
3.如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=_______, DA=_______.
A
B
E
D
C
4cm
6cm
随堂练
解:∵DE是△ABC边AB的垂直平分线,
∴EB=EA,
∴△AEC的周长
=AC+CE+EA
=AC+CE+EB
=AC+BC=4+5=9.
4.如图,DE是△ABC边AB的垂直平分线,交AB、BC于D、E,若AC=4,BC=5,求△AEC的周长.
A
D
B
E
C
随堂练
解:∵AD⊥BC,BD =DC,
∴AD 是BC 的垂直平分线,
∴AB =AC.
∵点C 在AE 的垂直平分线上,
∴AC =CE.∴AB =AC =CE.
∴AB+BD=CE+CD,即AB+BD=DE.
5.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
A
B
C
D
E
随堂练
分层练习-基础
1.如图是小甲在学完成语“箭在弦上”后绘制的一个简笔画,已知箭杆 CD 垂直平分 AB , AC =5 cm,则 BC 的长为( B )
A. 4 cm B. 5 cm
C. 6 cm D. 7 cm
B
2.[2024张家港期末]如图,在四边形 ABCD 中, AC 垂直平
分 BD ,垂足为点 E ,下列结论不一定成立的是( C )
C
A. AB = AD B. CA 平分∠ BCD C. AB = BC D. △ BEC ≌△ DEC
分层练习-基础
3.[2023青海]如图,在△ ABC 中, DE 是 BC 的垂直平分线.
若 AB =5, AC =8,则△ ABD 的周长是 .
13
4.[2024昆山期末]如图,线段 AB 的垂直平分线与 BC 的垂直平分线的交点 P 恰好在 AC 上,且 AC =10 cm,则 B 点到 P 点的距离为 .
5 cm
分层练习-基础
5. 【新考法·对称法·2024镇江京口区期中】如图,在△ ABC
中, AD 垂直平分 BC ,垂足为点 D ,点 E , F 是 AD 上的
两点,若△ ABC 的面积为6,则图中阴影部分的面积和
是 .
3
6.如图所示,已知在△ ABC 中, AB 与 AC 的垂直平分线分别交 AB 于点 D ,交 AC 于点 E ,它们相交于点 F ,求证: BF = FC .
证明:如图,连接 AF ,
∵ DF 是线段 AB 的垂直平分线,
∴ AF = BF ,
同理可得 AF = FC ,
∴ BF = FC .
分层练习-基础
分层练习-基础
7.如图,在9×9的网格中(每个小正方形的边长为1)有一个格点△ ABC . 利用网格线,画∠ CAB 的平分线,画 BC 的垂直平分线.
解:如图所示.
分层练习-巩固
8.如图,在△ ABC 中, AB = AC , D 是 BC 的中点, AC 的垂直平分线分别交 AC , AD , AB 于点 E , O , F ,则图中全等三角形的对数是( D )
A. 1对 B. 2对
C. 3对 D. 4对
D
分层练习-巩固
9.[2024南京江宁区月考]如图,在△ ABC 中,∠ BAC >90°, AB 的垂直平分线交 AB 于点 D ,交 BC 于点 E , AC 的垂直平分线交 AC 于点 F ,交 BC 于点 G . 若以 BE , EG , GC 的长为边长的三角形的面积为8,则△ ABC 的面积可能是( D )
A. 12 B. 14
C. 16 D. 18
D
分层练习-巩固
10.如图,在△ ABC 中, MP , NQ 分别垂直平分边 AB , AC ,交 BC 于点 P , Q ,如果 BC =20,那么△ APQ 的周长为 .
20
11.如图,在△ ABC 中, AD 垂直平分 BC ,交 BC 于点 E , CD ⊥ AC ,若 AB =4, CD =3, AD =5,则 BE = .
分层练习-巩固
12.[2024常州期末]在△ ABC 中, AB = AC , BC =10, AB
的垂直平分线与 AC 的垂直平分线分别交 BC 于点 D ,
E ,且 DE =4,则 AD + AE 的值为 .
6或14
分层练习-巩固
13.[2024扬州邗江区期末]如图, AB = CD ,线段 AC 的垂直平分线与线段 BD 的垂直平分线相交于点 E . 求证:∠ ABE =∠ CDE .
证明:如图,连接 AE , CE ,∵ AC , BD 的垂直平分线相交于 E ,∴ AE = CE , BE = DE ,
在△ ABE 和△ CDE 中,
∴△ ABE ≌△ CDE (SSS),
∴∠ ABE =∠ CDE .
分层练习-拓展
14. 【新考法·比较发现法】 如图,在△ ABC 中, D 是 BC 的中点,过 D 点的直线 GF 交 AC 于点 F ,交 AC 的平行线 BG 于 G 点, DE ⊥ DF ,交 AB 于点 E ,连接 EG 、 EF .
(1)求证: BG = CF ;
(1)证明:∵ BG ∥ AC ,∴∠ DBG =
∠ DCF . ∵ D 为 BC 的中点,∴ BD =
CD ,又∵∠ BDG =∠ CDF ,
∴△ BGD ≌△ CFD (ASA).∴ BG = CF .
分层练习-拓展
(2)请你判断 BE + CF 与 EF 的大小关系,并说明理由.
(2)解: BE + CF > EF . 理由如下:
∵△ BGD ≌△ CFD ,∴ GD = FD , BG = CF . 又∵ DE ⊥ FG ,∴ EG = EF . ∵在△ EBG 中, BE + BG > EG ,∴ BE + CF > EF .
课堂反馈
平分
相等
轴对称
垂直平分线
C
课堂反馈
课堂小结
线段垂直平分线的性质
内容
线段垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
第一课时 线段垂直平分线的性质
八年级苏科版数学上册 第二章 轴对称与轴对称图形
2.4 线段、角的轴对称性
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.理解线段的垂直平分线的相关概念. (重点)
2.掌握线段垂直平分线的定义. (重点)
3.利用线段的垂直平分线的性质解决问题.
(重点、难点)
情景导入
1.什么样的图形叫作轴对称图形?
把一个图形沿着某条直线对折,如果对折的两部分是完全重合的,我们就称这样的图形为轴对称图形,这条直线叫作这个图形的对称轴.
旧知回顾
这里有一条线段,它是轴对称图形吗?
a
b
l
对称轴l与线段ab之间存在某种关系呢?
某市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等.
情景导入
A
B
C
1.线段的垂直平分线
新知探究
如右图,直线l是线段AB的垂直平分线,l交AB于点O.把OA沿直线l翻折,因为∠1=∠2=90°,OA=OB,所以 OA 与OB 重合.
A
B
l
O
1
2
线段是轴对称图形,线段的垂直平分线是它的对称轴.
垂直于一条线段,并且平分这条线段的直线,叫作这条线段的垂直平分线.
线段的垂直平分线
l
l
思考探究
如下图,线段 AB 的垂直平分线l交 AB 于点 O,点 P 在l上.
PA 与 PB 相等吗?
A
P
B
O
P
B(A)
O
A
B
O
C
A
O
B
P
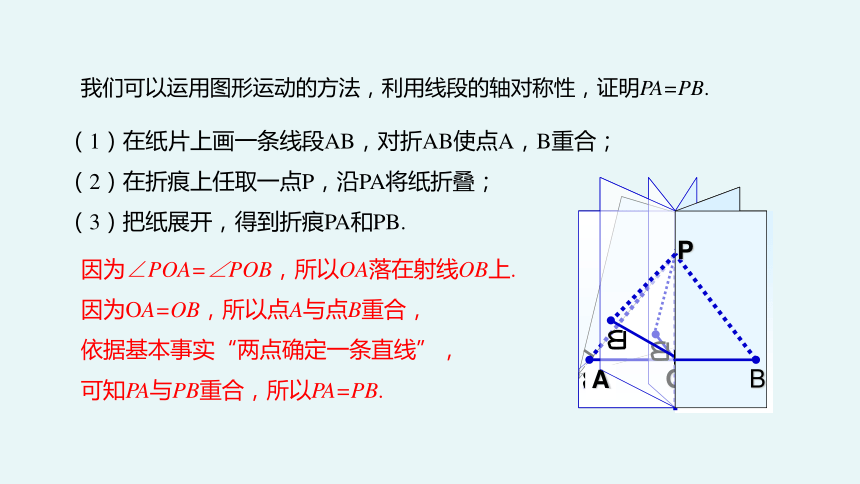
我们可以运用图形运动的方法,利用线段的轴对称性,证明PA=PB.
(1)在纸片上画一条线段AB,对折AB使点A,B重合;
(2)在折痕上任取一点P,沿PA将纸折叠;
(3)把纸展开,得到折痕PA和PB.
因为∠POA=∠POB,所以OA落在射线OB上.
因为OA=OB,所以点A与点B重合,
依据基本事实“两点确定一条直线”,
可知PA与PB重合,所以PA=PB.
典例剖析
A
B
P
M
N
O
例1.已知:直线MN⊥AB,垂足为O,且AO=OB.点P在MN上.你能得到 PA=PB吗
解:能得到 PA=PB
∵MN⊥AB ∴∠POA=∠POB=90o
在 ΔPOC和Δ POC中,
AO=BO
∠ POA= ∠ POB ;PO=PO
∴ ΔPAO ≌Δ PBO ∴PA=PB
∵ MN⊥AB,AO=OB.点P在MN上.
∴ PA=PB(线段垂直平分线上的点和这条线段两个端点的距离相等)
概念归纳
于是,我们得到如下定理:
线段垂直平分线上的点到线段两端的距离相等
几何语言
如右图,∵点A在线段BC的垂直平分线上,
∴ AB=AC.
易错提醒
线段有两条对称轴,线段的垂直平分线是它的对称轴,线段自身所在的直线也是它的对称轴.
l
B
A
C
D
概念归纳
特别注意:
线段垂直平分线的性质中的“ 距离”是“该点与
这条线段两个端点的距离”.
2. 用线段垂直平分线的性质可直接证明线段相等,
不必再用三角形全等来证明,因此它为证明线段
相等提供了新方法.
如右图,点P在线段AB的垂直平分线l外,PA交l于点Q,连接QB.
因为点Q在AB的垂直平分线上,
所以QA= QB,
于是PA= PQ+ QA =PQ +QB > PB.
例2.线段垂直平分线上外点,到这条线段两端的距离相等吗 为什么
解:不相等;因为到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
B
l
P
Q
●
●
A
课本例题
练一练
1.[月考·江阴] 如图2.4-2,在△ABC中,AB边的垂直平分线DE,分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG,分别与BC边和AC边交于点F和点G,又△BEG的周长为16,且GE=1,
则AC的长为( )
A. 16 B. 15
C. 14 D. 13
C
分析:利用线段垂直平分线的性质进行线段间的转化是一种常用的解题方法.本题中解题的关键是利用线段垂直平分线的性质, 将△BEG的周长转化为线段 AC+2GE的长,最后代入求解.
我们回到导入的问题
某市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等.
B
A
C
p
PA=PB=PC
转化为数学模型
∴购物中心建在P点处与三个小区的距离相等
A
B
C
2.已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
试说明PA=PB=PC吗
解:∵点P在线段AB的垂直平分线MN上,
∴PA=PB(性质定理).
同理 PB=PC.
∴PA=PB=PC.
B
A
C
M
N
P
M'
N'
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
练一练
归纳总结
1.垂直于一条线段,并且平分这条线段的直线,叫作
这条线段的垂直平分线.
线段的垂直平分线
2.线段垂直平分线的性质:
线段垂直平分线上的点
到这条线段两个端点的
距离相等.
3 线段的对称轴是这条线段的垂直平分线.
A
B
O
1.如图,直线CD是线段PB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
P
A
B
C
D
B
随堂练
2.如图,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
10cm
A
B
C
D
E
3.如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=_______, DA=_______.
A
B
E
D
C
4cm
6cm
随堂练
解:∵DE是△ABC边AB的垂直平分线,
∴EB=EA,
∴△AEC的周长
=AC+CE+EA
=AC+CE+EB
=AC+BC=4+5=9.
4.如图,DE是△ABC边AB的垂直平分线,交AB、BC于D、E,若AC=4,BC=5,求△AEC的周长.
A
D
B
E
C
随堂练
解:∵AD⊥BC,BD =DC,
∴AD 是BC 的垂直平分线,
∴AB =AC.
∵点C 在AE 的垂直平分线上,
∴AC =CE.∴AB =AC =CE.
∴AB+BD=CE+CD,即AB+BD=DE.
5.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
A
B
C
D
E
随堂练
分层练习-基础
1.如图是小甲在学完成语“箭在弦上”后绘制的一个简笔画,已知箭杆 CD 垂直平分 AB , AC =5 cm,则 BC 的长为( B )
A. 4 cm B. 5 cm
C. 6 cm D. 7 cm
B
2.[2024张家港期末]如图,在四边形 ABCD 中, AC 垂直平
分 BD ,垂足为点 E ,下列结论不一定成立的是( C )
C
A. AB = AD B. CA 平分∠ BCD C. AB = BC D. △ BEC ≌△ DEC
分层练习-基础
3.[2023青海]如图,在△ ABC 中, DE 是 BC 的垂直平分线.
若 AB =5, AC =8,则△ ABD 的周长是 .
13
4.[2024昆山期末]如图,线段 AB 的垂直平分线与 BC 的垂直平分线的交点 P 恰好在 AC 上,且 AC =10 cm,则 B 点到 P 点的距离为 .
5 cm
分层练习-基础
5. 【新考法·对称法·2024镇江京口区期中】如图,在△ ABC
中, AD 垂直平分 BC ,垂足为点 D ,点 E , F 是 AD 上的
两点,若△ ABC 的面积为6,则图中阴影部分的面积和
是 .
3
6.如图所示,已知在△ ABC 中, AB 与 AC 的垂直平分线分别交 AB 于点 D ,交 AC 于点 E ,它们相交于点 F ,求证: BF = FC .
证明:如图,连接 AF ,
∵ DF 是线段 AB 的垂直平分线,
∴ AF = BF ,
同理可得 AF = FC ,
∴ BF = FC .
分层练习-基础
分层练习-基础
7.如图,在9×9的网格中(每个小正方形的边长为1)有一个格点△ ABC . 利用网格线,画∠ CAB 的平分线,画 BC 的垂直平分线.
解:如图所示.
分层练习-巩固
8.如图,在△ ABC 中, AB = AC , D 是 BC 的中点, AC 的垂直平分线分别交 AC , AD , AB 于点 E , O , F ,则图中全等三角形的对数是( D )
A. 1对 B. 2对
C. 3对 D. 4对
D
分层练习-巩固
9.[2024南京江宁区月考]如图,在△ ABC 中,∠ BAC >90°, AB 的垂直平分线交 AB 于点 D ,交 BC 于点 E , AC 的垂直平分线交 AC 于点 F ,交 BC 于点 G . 若以 BE , EG , GC 的长为边长的三角形的面积为8,则△ ABC 的面积可能是( D )
A. 12 B. 14
C. 16 D. 18
D
分层练习-巩固
10.如图,在△ ABC 中, MP , NQ 分别垂直平分边 AB , AC ,交 BC 于点 P , Q ,如果 BC =20,那么△ APQ 的周长为 .
20
11.如图,在△ ABC 中, AD 垂直平分 BC ,交 BC 于点 E , CD ⊥ AC ,若 AB =4, CD =3, AD =5,则 BE = .
分层练习-巩固
12.[2024常州期末]在△ ABC 中, AB = AC , BC =10, AB
的垂直平分线与 AC 的垂直平分线分别交 BC 于点 D ,
E ,且 DE =4,则 AD + AE 的值为 .
6或14
分层练习-巩固
13.[2024扬州邗江区期末]如图, AB = CD ,线段 AC 的垂直平分线与线段 BD 的垂直平分线相交于点 E . 求证:∠ ABE =∠ CDE .
证明:如图,连接 AE , CE ,∵ AC , BD 的垂直平分线相交于 E ,∴ AE = CE , BE = DE ,
在△ ABE 和△ CDE 中,
∴△ ABE ≌△ CDE (SSS),
∴∠ ABE =∠ CDE .
分层练习-拓展
14. 【新考法·比较发现法】 如图,在△ ABC 中, D 是 BC 的中点,过 D 点的直线 GF 交 AC 于点 F ,交 AC 的平行线 BG 于 G 点, DE ⊥ DF ,交 AB 于点 E ,连接 EG 、 EF .
(1)求证: BG = CF ;
(1)证明:∵ BG ∥ AC ,∴∠ DBG =
∠ DCF . ∵ D 为 BC 的中点,∴ BD =
CD ,又∵∠ BDG =∠ CDF ,
∴△ BGD ≌△ CFD (ASA).∴ BG = CF .
分层练习-拓展
(2)请你判断 BE + CF 与 EF 的大小关系,并说明理由.
(2)解: BE + CF > EF . 理由如下:
∵△ BGD ≌△ CFD ,∴ GD = FD , BG = CF . 又∵ DE ⊥ FG ,∴ EG = EF . ∵在△ EBG 中, BE + BG > EG ,∴ BE + CF > EF .
课堂反馈
平分
相等
轴对称
垂直平分线
C
课堂反馈
课堂小结
线段垂直平分线的性质
内容
线段垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
