2.4线段、角的轴对称性(第2课时线段垂直平分线的判定)(教学课件)(共33张PPT)-八年级数学上册考试满分全攻略同步备课备考系列(苏科版)
文档属性
| 名称 | 2.4线段、角的轴对称性(第2课时线段垂直平分线的判定)(教学课件)(共33张PPT)-八年级数学上册考试满分全攻略同步备课备考系列(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-26 20:42:32 | ||
图片预览










文档简介
(共33张PPT)
第二课时 线段垂直平分线的判定
八年级苏科版数学上册 第二章 轴对称与轴对称图形
2.4 线段、角的轴对称性
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.理解线段的垂直平分线的判定定理. (重点)
2.掌握线段的垂直平分线的判定定理. (重点)
3.能用线段的垂直平分线的判定定理解决现实生活中的问题(重点、难点)
情景导入
旧知回顾
垂直于一条线段,并且平分这条线段的直线,叫作这条线段的垂直平分线.
1.什么叫做线段的垂直平分线?
2.线段是 图形,线段的垂直平分线是它的 .
轴对称
对称轴
3.线段垂直平分线的性质定理是什么?
线段垂直平分线上的点到线段两端的距离相等
4.这个性质定理可以用来证明 不必再用三角形全等来证明.
线段相等
上节课我们学习了线段垂直平分线的性质定理,回顾一下内容,回答下列问题.
M
情景导入
请在纸上画一条线段AB.
你能找出与线段AB的端点A、B距离相等的点吗?
这样的点有多少个?
A
B
M
点M到线段AB两端的距离相等,
那么点M是在这条线段的垂直平分线上吗?
本节课我们就来探讨一下这个问题吧!
M
无穷个
1.线段垂直平分线的判定定理
新知探究
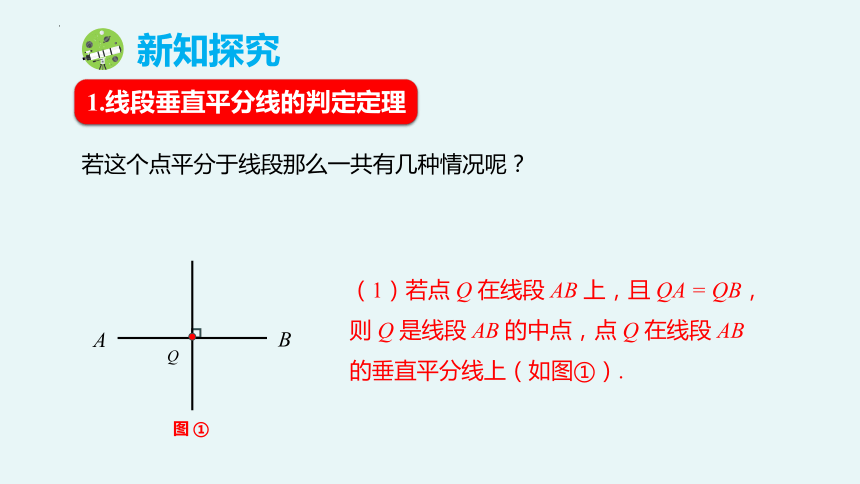
(1)若点 Q 在线段 AB 上,且 QA = QB,则 Q 是线段 AB 的中点,点 Q 在线段 AB 的垂直平分线上(如图①).
Q
A
B
若这个点平分于线段那么一共有几种情况呢?
图 ①
(2)若点 Q 在线段AB 外,且 QA=QB,则作 QM⊥AB,垂足为 M(如图②).由∠QMA=∠QMB=90°,QA=QB,QM=QM,
可证Rt△QAM≌Rt△QBM(HL).
由此可知AM=BM,即点Q在线段AB的垂直平分线上.
M
B
A
Q
概念归纳
几何语言
∵ QA=QB
∴ 点Q是线段AB的垂直平分线上的点.
由此我们得到线段垂直平分线的判定定理:
到线段两端的距离相等的点在线段垂直平分线上.
M
B
A
Q
知识拓展
(1)线段的垂直平分线是到线段两端距离相等的点的集合;
(2)三角形三边的垂直平分线相交于一点,这一点到三角形三个顶点的距离都相等.
概念归纳
典例剖析
例1.如下图,AD为∠BAC的平分线,交BC于点D,AE=AF.
请判断线段AD所在的直线是否为线段EF 的垂直平分线,若是,请给予证明;若不是,请说明理由.
分析:由线段垂直平分线的判定可知,证明AD所在的直线上的点A和点D到线段EF的两个端点的距离相等即可.
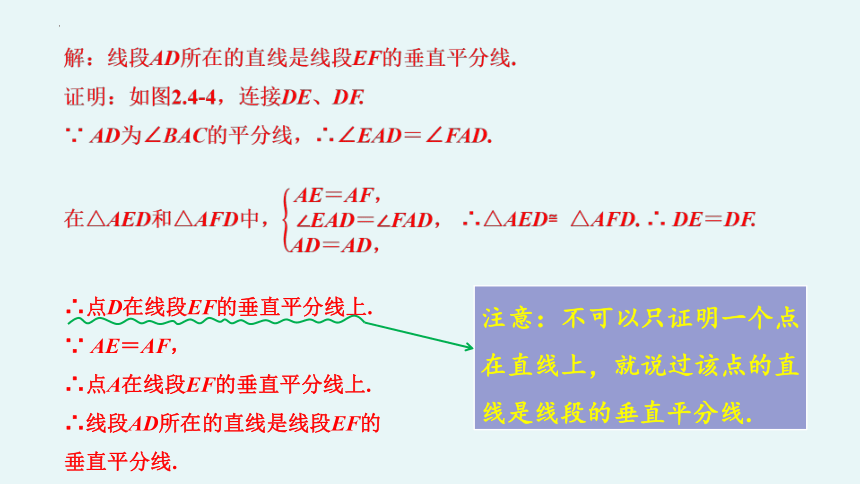
解:线段AD所在的直线是线段EF的垂直平分线.
证明:如图2.4-4,连接DE、DF.
∵ AD为∠BAC的平分线,∴∠EAD=∠FAD.
在△AED和△AFD中,∴△AED≌△AFD. ∴ DE=DF.
∴点D在线段EF的垂直平分线上.
∵ AE=AF,
∴点A在线段EF的垂直平分线上.
∴线段AD所在的直线是线段EF的
垂直平分线.
注意:不可以只证明一个点在直线上,就说过该点的直线是线段的垂直平分线.
特别提醒
证明一个点在一条线段的垂直平分线上,还可以利用线段垂直平分线的定义进行推理,思路有两种:一是作垂直,证平分;二是取中点,证垂直.
概念归纳
概念归纳
判断线段垂直平分线的两种方法:
一是定义法,二是判定定理.
一般习惯用定义法进行判断,而利用判定定理判断更简单. 用判定定理判定一条直线是线段的垂直平分线时,一定要证明直线上有两个不同的点到线段两个端点的距离相等.
2.线段垂直平分线的画法
新知探究
用尺规作线段AB的垂直平分线的画法:
(1)分别以点A、B为圆心,大于AB的长为
半径画弧,两弧相交于点C、D;
(2)过C、D两点作直线,
直线CD就是线段AB的垂直平分线,如右图所示
概念归纳
易错警示
作线段AB的垂直平分线时,必须以大于AB的长为半径画弧,否则所画的弧就不能相交或只有一个交点.
典例剖析
例2.在铁路a的同侧有两个工厂A和B,要在铁路边建一货场C,使A、B两个工厂到货场C的距离相等,试在下图中作出点C.
A
B
a
解:连接AB,作线段AB的垂直平分线交直线a于点C.
如下图, 点C即为所求.
概念归纳
方法点拨
尺规作图时要注意虚实线,即辅助性的线用虚线,所要画的线用实线,同时要注意保留作图痕迹.
随堂练
1.已知:如图,AB=AC,DB=DC,点E在AD上.求证:EB=EC.
解:因为AB=AC,DB=DC;
所以AD是线段BC的垂直平分线;
(线段的垂直平分线的判定定理)
因为点E在AD上;
所以EB=EC.
(线段的垂直平分线的性质定理)
到线段两端点距离相等的点在线段的垂直平分线上
随堂练
分层练习-基础
1.如图, AC = AD , BC = BD ,那么下列判断正确的是( B )
A. CD 垂直平分 AB
B. AB 垂直平分 CD
C. CD 平分∠ ACB
D. ∠ ACB =∠ ADB =90°
B
2.[2024无锡梁溪区期中]如果一个三角形三边垂直平分线的交点在三角形外部,那么这个三角形是( C )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 不能确定
C
分层练习-基础
3.[2024苏州吴中区月考]在如图所示的方格纸中,每个小方格都是边长为1的正方形, A , B 是方格纸中的两个格点(即正方形的顶点).在这张5×5的方格纸中,找出格点 C ,使△ ABC 为等腰三角形,则满足条件的格点 C 有( C )
A. 3个 B. 5个
C. 6个 D. 8个
C
分层练习-基础
4. 如图,点 D 在△ ABC 的边 BC 上,如果 DB = DA ,那么点 D 在线段 的垂直平分线上;如果 BC = BD + AD ,那么点 D 在线段 的垂直平分线上.
AB
AC
分层练习-基础
5. [2024扬州江都区期中]如图,在△ ABC 中,分别以点 B 和点 C 为圆心,大于 BC 长为半径画弧,两弧相交于点 M 、 N . 作直线 MN ,交 AC 于点 D ,交 BC 于点 E ,连接 BD . 若 AB =7, AC =12, BC =6,则△ ABD 的周长为 .
19
分层练习-基础
6.[2024江阴月考]如图,在△ ABC 中, AB = AC , G 为三角形外一点,且 GB = GC . (1)求证:直线 AG 垂直平分 BC ;
证明:(1)∵ GB = GC , AB = AC ,
∴点 G 、点 A 在 BC 的垂直平分线上.
又∵两点确定一条直线,
∴直线 AG 垂直平分 BC .
(2)点 D 在 AG 上,求证: DB = DC .
证明:(2)∵ AG 垂直平分 BC ,点 D 在 AG
上,∴ DB = DC .
证明:∵ BE ∥ AC ,∴∠ E =∠ DCO ,
在△ BOE 和△ DOC 中
∴△ BOE ≌△ DOC (AAS),∴ OB = OD ,∴点 O 在 BD 的垂直平分线上.
∵ AB = AD ,∴点 A 在 BD 的垂直平分线上,∴ AO 垂直平分 BD .
分层练习-巩固
7. 如图,点 D 是△ ABC 边 AC 上一点, AD = AB ,过 B 点作 BE ∥ AC ,且 BE = CD ,连接 CE 交 BD 于点 O ,连接 AO .
求证: AO 垂直平分 BD .
分层练习-巩固
8.[2024扬州广陵区月考]如图,已知△ ABC ,点 P 为∠ BAC 的平分线上一点, PE ⊥ AB , PF ⊥ AC ,垂足分别为点 E , F .
(1)求证: PE = PF ;
证明:(1)∵点 P 为∠ BAC 的平分线上一点,
∴∠ BAP =∠ FAP ,∵ PE ⊥ AB , PF ⊥ AF
∴∠ PEA =∠ PFA =90°,在△ APE 和△ APF
中,
∴△ APE ≌△ APF (AAS),∴ PE = PF .
分层练习-巩固
(2)若 BE = CF ,求证:点 P 在 BC 的垂直平分线上.
证明:(2)连接 PB , PC ,如图,
∵ PE ⊥ AB , PF ⊥ AF ,
∴∠ BEP =∠ CFP =90°,由(1)知
PE = PF . 又∵ BE = CF ,
∴△ BEP ≌△ CFP (SAS),∴ BP = CP ,∴点 P 在 BC 的垂直平分线上.
分层练习-巩固
9.[2024南京玄武区期中]如图,已知P 是直线 l 外一点,用两种不同的方法求作一点 Q ,使得点 Q 到点 P 的距离和点 Q 到直线 l 的距离相等.(要求:用直尺和圆规作图,保留作图痕迹)
解:如图,点 Q 为所作.(答案不唯一)
分层练习-拓展
10. 【新考法·阅读理解法】 如果三角形三边的长 a , b , c 满足 = b ,那么我们就把这样的三角形叫做“匀称三角形”,如三边长分别为1,1,1或3,5,7……的三角形都是“匀称三角形”.如图,两条线段的长分别为 a , c ( a < c ).用直尺和圆规作一个最短边、最长边的长分别为 a , c 的“匀称三角形”.(不写作法,保留作图痕迹)
分层练习-拓展
解:如图,△ ABC 为所作.
在线段的垂直平分线上
AC
40°或140°
课堂反馈
课堂反馈
课堂小结
1.线段的垂直平分线的判定定理:
到线段两端的距离相等的点在线段垂直平分线上.
2.用尺规作图做出线段的垂直平分线.
第二课时 线段垂直平分线的判定
八年级苏科版数学上册 第二章 轴对称与轴对称图形
2.4 线段、角的轴对称性
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.理解线段的垂直平分线的判定定理. (重点)
2.掌握线段的垂直平分线的判定定理. (重点)
3.能用线段的垂直平分线的判定定理解决现实生活中的问题(重点、难点)
情景导入
旧知回顾
垂直于一条线段,并且平分这条线段的直线,叫作这条线段的垂直平分线.
1.什么叫做线段的垂直平分线?
2.线段是 图形,线段的垂直平分线是它的 .
轴对称
对称轴
3.线段垂直平分线的性质定理是什么?
线段垂直平分线上的点到线段两端的距离相等
4.这个性质定理可以用来证明 不必再用三角形全等来证明.
线段相等
上节课我们学习了线段垂直平分线的性质定理,回顾一下内容,回答下列问题.
M
情景导入
请在纸上画一条线段AB.
你能找出与线段AB的端点A、B距离相等的点吗?
这样的点有多少个?
A
B
M
点M到线段AB两端的距离相等,
那么点M是在这条线段的垂直平分线上吗?
本节课我们就来探讨一下这个问题吧!
M
无穷个
1.线段垂直平分线的判定定理
新知探究
(1)若点 Q 在线段 AB 上,且 QA = QB,则 Q 是线段 AB 的中点,点 Q 在线段 AB 的垂直平分线上(如图①).
Q
A
B
若这个点平分于线段那么一共有几种情况呢?
图 ①
(2)若点 Q 在线段AB 外,且 QA=QB,则作 QM⊥AB,垂足为 M(如图②).由∠QMA=∠QMB=90°,QA=QB,QM=QM,
可证Rt△QAM≌Rt△QBM(HL).
由此可知AM=BM,即点Q在线段AB的垂直平分线上.
M
B
A
Q
概念归纳
几何语言
∵ QA=QB
∴ 点Q是线段AB的垂直平分线上的点.
由此我们得到线段垂直平分线的判定定理:
到线段两端的距离相等的点在线段垂直平分线上.
M
B
A
Q
知识拓展
(1)线段的垂直平分线是到线段两端距离相等的点的集合;
(2)三角形三边的垂直平分线相交于一点,这一点到三角形三个顶点的距离都相等.
概念归纳
典例剖析
例1.如下图,AD为∠BAC的平分线,交BC于点D,AE=AF.
请判断线段AD所在的直线是否为线段EF 的垂直平分线,若是,请给予证明;若不是,请说明理由.
分析:由线段垂直平分线的判定可知,证明AD所在的直线上的点A和点D到线段EF的两个端点的距离相等即可.
解:线段AD所在的直线是线段EF的垂直平分线.
证明:如图2.4-4,连接DE、DF.
∵ AD为∠BAC的平分线,∴∠EAD=∠FAD.
在△AED和△AFD中,∴△AED≌△AFD. ∴ DE=DF.
∴点D在线段EF的垂直平分线上.
∵ AE=AF,
∴点A在线段EF的垂直平分线上.
∴线段AD所在的直线是线段EF的
垂直平分线.
注意:不可以只证明一个点在直线上,就说过该点的直线是线段的垂直平分线.
特别提醒
证明一个点在一条线段的垂直平分线上,还可以利用线段垂直平分线的定义进行推理,思路有两种:一是作垂直,证平分;二是取中点,证垂直.
概念归纳
概念归纳
判断线段垂直平分线的两种方法:
一是定义法,二是判定定理.
一般习惯用定义法进行判断,而利用判定定理判断更简单. 用判定定理判定一条直线是线段的垂直平分线时,一定要证明直线上有两个不同的点到线段两个端点的距离相等.
2.线段垂直平分线的画法
新知探究
用尺规作线段AB的垂直平分线的画法:
(1)分别以点A、B为圆心,大于AB的长为
半径画弧,两弧相交于点C、D;
(2)过C、D两点作直线,
直线CD就是线段AB的垂直平分线,如右图所示
概念归纳
易错警示
作线段AB的垂直平分线时,必须以大于AB的长为半径画弧,否则所画的弧就不能相交或只有一个交点.
典例剖析
例2.在铁路a的同侧有两个工厂A和B,要在铁路边建一货场C,使A、B两个工厂到货场C的距离相等,试在下图中作出点C.
A
B
a
解:连接AB,作线段AB的垂直平分线交直线a于点C.
如下图, 点C即为所求.
概念归纳
方法点拨
尺规作图时要注意虚实线,即辅助性的线用虚线,所要画的线用实线,同时要注意保留作图痕迹.
随堂练
1.已知:如图,AB=AC,DB=DC,点E在AD上.求证:EB=EC.
解:因为AB=AC,DB=DC;
所以AD是线段BC的垂直平分线;
(线段的垂直平分线的判定定理)
因为点E在AD上;
所以EB=EC.
(线段的垂直平分线的性质定理)
到线段两端点距离相等的点在线段的垂直平分线上
随堂练
分层练习-基础
1.如图, AC = AD , BC = BD ,那么下列判断正确的是( B )
A. CD 垂直平分 AB
B. AB 垂直平分 CD
C. CD 平分∠ ACB
D. ∠ ACB =∠ ADB =90°
B
2.[2024无锡梁溪区期中]如果一个三角形三边垂直平分线的交点在三角形外部,那么这个三角形是( C )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 不能确定
C
分层练习-基础
3.[2024苏州吴中区月考]在如图所示的方格纸中,每个小方格都是边长为1的正方形, A , B 是方格纸中的两个格点(即正方形的顶点).在这张5×5的方格纸中,找出格点 C ,使△ ABC 为等腰三角形,则满足条件的格点 C 有( C )
A. 3个 B. 5个
C. 6个 D. 8个
C
分层练习-基础
4. 如图,点 D 在△ ABC 的边 BC 上,如果 DB = DA ,那么点 D 在线段 的垂直平分线上;如果 BC = BD + AD ,那么点 D 在线段 的垂直平分线上.
AB
AC
分层练习-基础
5. [2024扬州江都区期中]如图,在△ ABC 中,分别以点 B 和点 C 为圆心,大于 BC 长为半径画弧,两弧相交于点 M 、 N . 作直线 MN ,交 AC 于点 D ,交 BC 于点 E ,连接 BD . 若 AB =7, AC =12, BC =6,则△ ABD 的周长为 .
19
分层练习-基础
6.[2024江阴月考]如图,在△ ABC 中, AB = AC , G 为三角形外一点,且 GB = GC . (1)求证:直线 AG 垂直平分 BC ;
证明:(1)∵ GB = GC , AB = AC ,
∴点 G 、点 A 在 BC 的垂直平分线上.
又∵两点确定一条直线,
∴直线 AG 垂直平分 BC .
(2)点 D 在 AG 上,求证: DB = DC .
证明:(2)∵ AG 垂直平分 BC ,点 D 在 AG
上,∴ DB = DC .
证明:∵ BE ∥ AC ,∴∠ E =∠ DCO ,
在△ BOE 和△ DOC 中
∴△ BOE ≌△ DOC (AAS),∴ OB = OD ,∴点 O 在 BD 的垂直平分线上.
∵ AB = AD ,∴点 A 在 BD 的垂直平分线上,∴ AO 垂直平分 BD .
分层练习-巩固
7. 如图,点 D 是△ ABC 边 AC 上一点, AD = AB ,过 B 点作 BE ∥ AC ,且 BE = CD ,连接 CE 交 BD 于点 O ,连接 AO .
求证: AO 垂直平分 BD .
分层练习-巩固
8.[2024扬州广陵区月考]如图,已知△ ABC ,点 P 为∠ BAC 的平分线上一点, PE ⊥ AB , PF ⊥ AC ,垂足分别为点 E , F .
(1)求证: PE = PF ;
证明:(1)∵点 P 为∠ BAC 的平分线上一点,
∴∠ BAP =∠ FAP ,∵ PE ⊥ AB , PF ⊥ AF
∴∠ PEA =∠ PFA =90°,在△ APE 和△ APF
中,
∴△ APE ≌△ APF (AAS),∴ PE = PF .
分层练习-巩固
(2)若 BE = CF ,求证:点 P 在 BC 的垂直平分线上.
证明:(2)连接 PB , PC ,如图,
∵ PE ⊥ AB , PF ⊥ AF ,
∴∠ BEP =∠ CFP =90°,由(1)知
PE = PF . 又∵ BE = CF ,
∴△ BEP ≌△ CFP (SAS),∴ BP = CP ,∴点 P 在 BC 的垂直平分线上.
分层练习-巩固
9.[2024南京玄武区期中]如图,已知P 是直线 l 外一点,用两种不同的方法求作一点 Q ,使得点 Q 到点 P 的距离和点 Q 到直线 l 的距离相等.(要求:用直尺和圆规作图,保留作图痕迹)
解:如图,点 Q 为所作.(答案不唯一)
分层练习-拓展
10. 【新考法·阅读理解法】 如果三角形三边的长 a , b , c 满足 = b ,那么我们就把这样的三角形叫做“匀称三角形”,如三边长分别为1,1,1或3,5,7……的三角形都是“匀称三角形”.如图,两条线段的长分别为 a , c ( a < c ).用直尺和圆规作一个最短边、最长边的长分别为 a , c 的“匀称三角形”.(不写作法,保留作图痕迹)
分层练习-拓展
解:如图,△ ABC 为所作.
在线段的垂直平分线上
AC
40°或140°
课堂反馈
课堂反馈
课堂小结
1.线段的垂直平分线的判定定理:
到线段两端的距离相等的点在线段垂直平分线上.
2.用尺规作图做出线段的垂直平分线.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
