湖南省邵阳市邵阳县石齐学校2015-2016学年高一上学期第三次月考数学(185班)试题(无答案)
文档属性
| 名称 | 湖南省邵阳市邵阳县石齐学校2015-2016学年高一上学期第三次月考数学(185班)试题(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 134.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-17 18:59:41 | ||
图片预览

文档简介
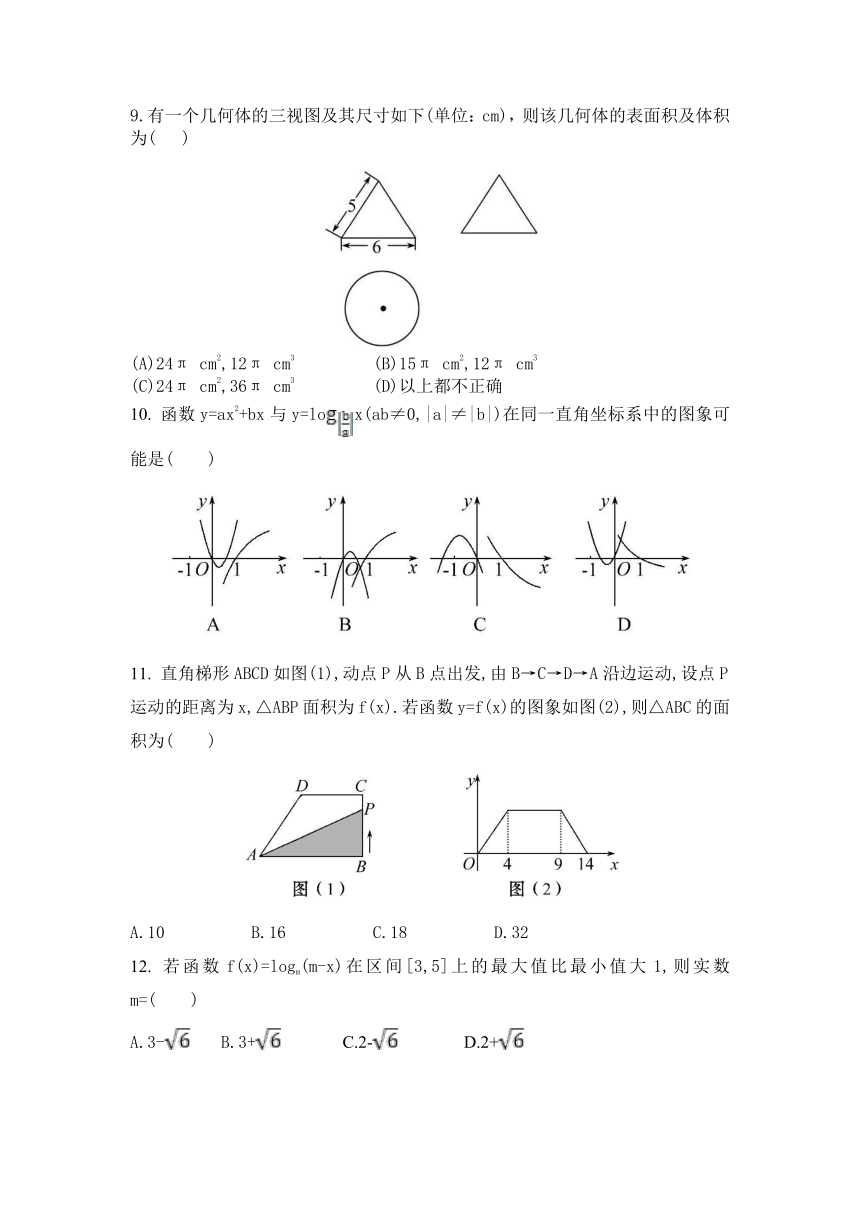
185班数学测试题
时间:120分钟 总分:150分
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 下列各组函数是同一函数的是( )
A.y=与y=1 B.y=|x-1|与y=
C.y=|x|+|x-1|与y=2x-1 D.y=与y=x
2. 函数f(x)=lnx+x3-9的零点所在的区间为( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
3.如图是由哪个平面图形旋转得到的( )
( http: / / www.21cnjy.com )
4. 若函数f(x)=(2m+3)是幂函数,则m的值为( )
A.-1 B.0 C.1 D.2
5.已知各顶点都在一个球面上的正四棱柱(其底面是正方形,且侧棱垂直于底面)高为4,体积为16,则这个球的表面积是( )
(A)16π (B)20π (C)24π (D)32π
6.下列说法正确的是( )
(A)圆锥的侧面展开图是一个等腰三角形
(B)棱柱即是两个底面全等且其余各面都是矩形的多面体
(C)任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥
(D)通过圆台侧面上一点,有无数条母线
7.如图所示的直观图的平面图形ABCD是( )
(A)任意梯形
(B)直角梯形
(C)任意四边形
(D)平行四边形
8. 已知函数f(x)=x2+ax-4在区间(0,1)内只有一个零点,则a的取值范围是( )
A.(-∞,3) B.(3, +∞) C.(-∞,4) D.(4,+∞)
9.有一个几何体的三视图及其尺寸如下(单位:cm),则该几何体的表面积及体积为( )
( http: / / www.21cnjy.com )
(A)24π cm2,12π cm3 (B)15π cm2,12π cm3
(C)24π cm2,36π cm3 (D)以上都不正确
10. 函数y=ax2+bx与y=lox(ab≠0,|a|≠|b|)在同一直角坐标系中的图象可能是( )
( http: / / www.21cnjy.com )
11. 直角梯形ABCD如图(1),动点P从B点出发,由B→C→D→A沿边运动,设点P运动的距离为x,△ABP面积为f(x).若函数y=f(x)的图象如图(2),则△ABC的面积为( )
( http: / / www.21cnjy.com )
A.10 B.16 C.18 D.32
12. 若函数f(x)=logm(m-x)在区间[3,5]上的最大值比最小值大1,则实数m=( )
A.3- B.3+ C.2- D.2+
二、填空题(本大题共4小题,每小题5分,共20分,请把正确答案填在题中的横线上)
13. = .
14.三棱柱ABC-A′B′C′的底面是 ( http: / / www.21cnjy.com )边长为1 cm 的正三角形,侧面是长方形,侧棱长为4 cm,一个小虫从A点出发沿表面一圈到达A′点,则小虫所行的最短路程为_______ cm.
15.在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离为_______.
16. 函数y=2log2x-1,x∈(0,4]的值域是 .
三、解答题(本大题共6小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)
17.(10分) 设A={x|-1≤x≤4},B={x|m-1(1)当x∈N*时,求A的子集的个数.
(2)当x∈R且A∩B=B时,求m的取值范围.
18.(12分) 已知函数f(x)=log3(ax+b)的图象经过点A(2,1),B(5,2).
(1)求函数f(x)的解析式及定义域.
(2)求f(14)÷f的值.
19. 如图是某几何体的三视图.
(1)画出它的直观图(不要求写画法);
(2)求这个几何体的表面积和体积.
20.如图(单位:cm),求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积.
( http: / / www.21cnjy.com )
21.(12分)正三棱锥的高为1,底面边长为,内有一个球与它的四个面都相切,求:
(1)棱锥的表面积;
(2)内切球的表面积与体积。
22.(12分) 已知函数f(x)对任意实数x,y都有f(xy)=f(x)f(y),且f(-1)=1,f(27)=9,当0≤x<1时,f(x)∈[0,1).
(1)判断f(x)的奇偶性.
(2)判断f(x)在[0,+∞)上的单调性,并给出证明.
(3)若a≥0且f(a+1)≤,求实数a的取值范围.
时间:120分钟 总分:150分
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 下列各组函数是同一函数的是( )
A.y=与y=1 B.y=|x-1|与y=
C.y=|x|+|x-1|与y=2x-1 D.y=与y=x
2. 函数f(x)=lnx+x3-9的零点所在的区间为( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
3.如图是由哪个平面图形旋转得到的( )
( http: / / www.21cnjy.com )
4. 若函数f(x)=(2m+3)是幂函数,则m的值为( )
A.-1 B.0 C.1 D.2
5.已知各顶点都在一个球面上的正四棱柱(其底面是正方形,且侧棱垂直于底面)高为4,体积为16,则这个球的表面积是( )
(A)16π (B)20π (C)24π (D)32π
6.下列说法正确的是( )
(A)圆锥的侧面展开图是一个等腰三角形
(B)棱柱即是两个底面全等且其余各面都是矩形的多面体
(C)任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥
(D)通过圆台侧面上一点,有无数条母线
7.如图所示的直观图的平面图形ABCD是( )
(A)任意梯形
(B)直角梯形
(C)任意四边形
(D)平行四边形
8. 已知函数f(x)=x2+ax-4在区间(0,1)内只有一个零点,则a的取值范围是( )
A.(-∞,3) B.(3, +∞) C.(-∞,4) D.(4,+∞)
9.有一个几何体的三视图及其尺寸如下(单位:cm),则该几何体的表面积及体积为( )
( http: / / www.21cnjy.com )
(A)24π cm2,12π cm3 (B)15π cm2,12π cm3
(C)24π cm2,36π cm3 (D)以上都不正确
10. 函数y=ax2+bx与y=lox(ab≠0,|a|≠|b|)在同一直角坐标系中的图象可能是( )
( http: / / www.21cnjy.com )
11. 直角梯形ABCD如图(1),动点P从B点出发,由B→C→D→A沿边运动,设点P运动的距离为x,△ABP面积为f(x).若函数y=f(x)的图象如图(2),则△ABC的面积为( )
( http: / / www.21cnjy.com )
A.10 B.16 C.18 D.32
12. 若函数f(x)=logm(m-x)在区间[3,5]上的最大值比最小值大1,则实数m=( )
A.3- B.3+ C.2- D.2+
二、填空题(本大题共4小题,每小题5分,共20分,请把正确答案填在题中的横线上)
13. = .
14.三棱柱ABC-A′B′C′的底面是 ( http: / / www.21cnjy.com )边长为1 cm 的正三角形,侧面是长方形,侧棱长为4 cm,一个小虫从A点出发沿表面一圈到达A′点,则小虫所行的最短路程为_______ cm.
15.在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离为_______.
16. 函数y=2log2x-1,x∈(0,4]的值域是 .
三、解答题(本大题共6小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)
17.(10分) 设A={x|-1≤x≤4},B={x|m-1
(2)当x∈R且A∩B=B时,求m的取值范围.
18.(12分) 已知函数f(x)=log3(ax+b)的图象经过点A(2,1),B(5,2).
(1)求函数f(x)的解析式及定义域.
(2)求f(14)÷f的值.
19. 如图是某几何体的三视图.
(1)画出它的直观图(不要求写画法);
(2)求这个几何体的表面积和体积.
20.如图(单位:cm),求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积.
( http: / / www.21cnjy.com )
21.(12分)正三棱锥的高为1,底面边长为,内有一个球与它的四个面都相切,求:
(1)棱锥的表面积;
(2)内切球的表面积与体积。
22.(12分) 已知函数f(x)对任意实数x,y都有f(xy)=f(x)f(y),且f(-1)=1,f(27)=9,当0≤x<1时,f(x)∈[0,1).
(1)判断f(x)的奇偶性.
(2)判断f(x)在[0,+∞)上的单调性,并给出证明.
(3)若a≥0且f(a+1)≤,求实数a的取值范围.
同课章节目录
