宁夏银川市2024-2025学年高二上学期入学考试数学试卷 (含解析)
文档属性
| 名称 | 宁夏银川市2024-2025学年高二上学期入学考试数学试卷 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 554.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-27 00:00:00 | ||
图片预览




文档简介
宁夏银川市2024-2025学年高二上学期入学数学试卷(解析版)
一、单选题(本题共8小题,每小题5分,共40分)
1.(5分)如果集合S={x|x=3n+1,n∈N},T={x|x=3k﹣2,k∈Z},则( )
A.S T B.T S C.S=T D.S T
2.(5分)不等式的解集为{x|x<﹣1或x>4},则的解集为( )
A. B.{x|﹣1≤x<1}
C. D.
3.(5分)已知f(x),g(x)是定义域为R的函数,且f(x)是奇函数,g(x)是偶函数,满足f(x)+g(x)=ax2+x+2,若对任意的1<x1<x2<2,都有成立,则实数a的取值范围是( )
A. B.
C. D.
4.(5分)若2024x﹣2024y<2025﹣x﹣2025﹣y,则( )
A.ln|x﹣y|>0 B.ln|x﹣y|<0
C.ln(y﹣x+1)>0 D.ln(y﹣x+1)<0
5.(5分)已知,为单位向量,且丄(+2),则向量与的夹角为( )
A.30° B.60° C.120° D.150°
6.(5分)若,则cos2A+cos2B的取值范围是( )
A. B. C. D.[0,1]
7.(5分)已知球O的表面积为16π,边长为3的等边△ABC的三个顶点都在球O的球面上,则三棱锥O﹣ABC的体积等于( )
A. B. C. D.
8.(5分)抛掷一颗骰子,设事件A:落地时向上的点数是奇数,事件B:落地时向上的点数是偶数,事件C:落地时向上的点数小于3,事件D:落地时向上的点数大于5,则下列每对事件中,不是互斥事件的是( )
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
A.A与B B.B与C C.A与D D.C与D
二、多选题(本题共4小题,每小题5分,共20分)
(多选)9.(5分)有6个相同的球,分别标有数字1,2,3,4,5,6,从中不放回的随机取两次,每次取1个球,事件A表示“第一次取出的球的数字是偶数”,事件B表示“第二次取出的球的数字是奇数”,事件C表示“两次取出的球的数字之和是偶数”,事件D表示“两次取出的球的数字之和是奇数”,则( )
A.A与B是互斥事件 B.C与D互为对立事件
C.B发生的概率为 D.B与C相互独立
(多选)10.(5分)如图,正方体ABCD﹣A1B1C1D1的棱长为2,则( )
A.BD∥平面CB1D1
B.AC1⊥平面CB1D1
C.异面直线CB1与BD所成的角为60°
D.三棱锥D﹣CB1D1的体积为
(多选)11.(5分)已知α,β是两个不重合的平面,m,n是两条不重合的直线,则下列命题中是真命题的是( )
A.如果m⊥n,m⊥α,n∥β,那么α⊥β
B.如果m⊥α,n∥α,那么m⊥n
C.如果α∥β,m α,那么m∥β
D.如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等
(多选)12.(5分)已知是函数f(x)=2asinxcosx﹣2cos2x﹣1的一个零点.则( )
A.a=
B.函数f(x)的值域为[﹣2,2]
C.函数f(x)的单调递减区间为,(k∈Z)
D.不等式f(x)≥0的解集为
三、填空题(本题共4小题,每小题5分,共20分)
13.(5分)甲、乙两水文站同时作水文预报,如果甲站、乙站各自预报的准确率分别为0.8和0.7,那么在一次预报中,甲站、乙站预报都错误的概率为 .
14.(5分)已知a>0,b>0,且9a+b=ab,则a+4b的最小值为 .
15.(5分)已知圆锥的顶点S和底面圆周都在球O的球面上,且母线长为2,A,B为其底面圆周上的两点,若△SAB面积的最大值为,则球O的表面积为 .
16.(5分)赵爽是我国古代数学家,大约在公元222年,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间一个小正方形组成).类比“赵爽弦图”,可构造如图所示的图形,它是由3个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形,设(λ,μ∈R),若DF=2AF,则= .
四、解答题(本题共6小题,共70分)
17.(10分)甲袋子中装有2个红球、1个白球,乙袋子中装有1个红球、2个白球(袋子不透明,球除颜色外完全一样).
(1)现从甲、乙两个袋子中各任选1个球,求选出的2个球的颜色相同的概率;
(2)从甲、乙两袋6个球中任选2个球,求选出的2个球来自同一袋子的概率.
18.(12分)如图,四棱锥P﹣ABCD的底面ABCD是直角梯形,PA⊥底面ABCD,AB∥CD,CD⊥BC,且.
(1)证明:平面PBC⊥平面PAB.
(2)求二面角A﹣BC﹣P的大小.
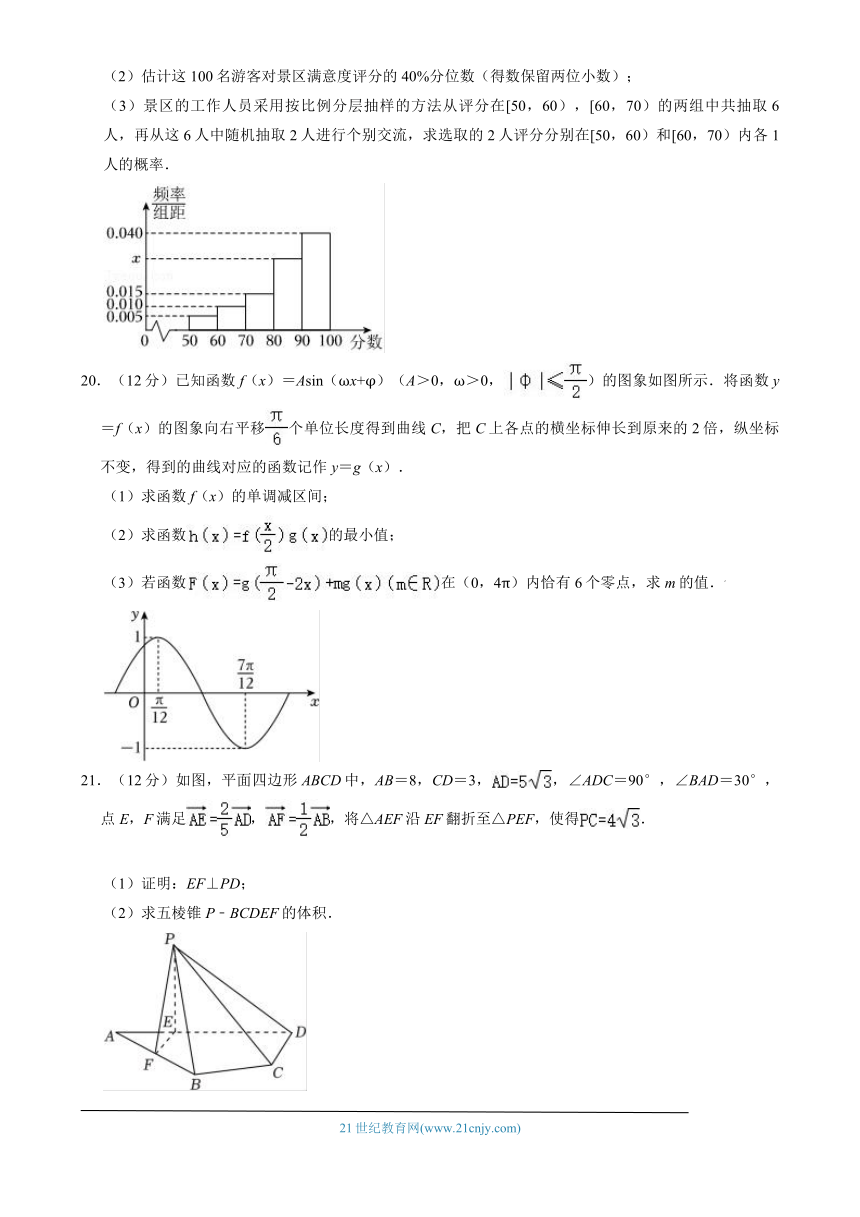
19.(12分)黄山原名“黟山”,因峰岩青黑,遥望苍黛而名,后因传说轩辕黄帝曾在此炼丹,故改名为“黄山”.黄山雄踞风景秀丽的安徽南部,是我国最著名的山岳风景区之一.明代旅行家、地理学家徐霞客两游黄山,赞叹说:“登黄山天下无山,观止矣!”又留“五岳归来不看山,黄山归来不看岳”的美誉.为更好地提升旅游品质,黄山风景区的工作人员随机选择100名游客对景区进行满意度评分(满分100分),根据评分,制成如图所示的频率分布直方图.
(1)根据频率分布直方图,求x的值;
(2)估计这100名游客对景区满意度评分的40%分位数(得数保留两位小数);
(3)景区的工作人员采用按比例分层抽样的方法从评分在[50,60),[60,70)的两组中共抽取6人,再从这6人中随机抽取2人进行个别交流,求选取的2人评分分别在[50,60)和[60,70)内各1人的概率.
20.(12分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的图象如图所示.将函数y=f(x)的图象向右平移个单位长度得到曲线C,把C上各点的横坐标伸长到原来的2倍,纵坐标不变,得到的曲线对应的函数记作y=g(x).
(1)求函数f(x)的单调减区间;
(2)求函数的最小值;
(3)若函数在(0,4π)内恰有6个零点,求m的值.
21.(12分)如图,平面四边形ABCD中,AB=8,CD=3,,∠ADC=90°,∠BAD=30°,点E,F满足,,将△AEF沿EF翻折至△PEF,使得.
(1)证明:EF⊥PD;
(2)求五棱锥P﹣BCDEF的体积.
22.(12分)某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25米,为了便于游客休闲散步,该农庄决定在鱼塘内建三条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°.
(1)设∠BOE=α,试将△OEF的周长l表示成α的函数关系式,并求出此函数的定义域;
(2)经核算,三条走廊每米建设费用均为4000元,试问如何设计才能使建设总费用最低并求出最低总费用.
参考答案与试题解析
一、单选题(本题共8小题,每小题5分,共40分)
1.(5分)如果集合S={x|x=3n+1,n∈N},T={x|x=3k﹣2,k∈Z},则( )
A.S T B.T S C.S=T D.S T
【分析】由S={x|x=3n+1,n∈N},T={x|x=3k﹣2,k∈+1,k∈Z},即可判断S和T的关系.
【解答】解:S={x|x=3n+1,n∈N},T={x|x=3k﹣2,k∈+1,k∈Z},
故S T,只有A正确.
故选:A.
【点评】本题考查集合与集合的关系的判断,属于基础题.
2.(5分)不等式的解集为{x|x<﹣1或x>4},则的解集为( )
A. B.{x|﹣1≤x<1} C. D.
【分析】将不等式化为(ax﹣x﹣b+1)(x+b)>0,即(ax﹣x﹣b+1)(x+b)=0的两个根为x1=﹣1,x2=4,代入求出a,b,再利用分式不等式的解法即可求解.
【解答】解:不等式可转化为[(a﹣1)x﹣b+1](x+b)>0,
其解集为{x|x<﹣1或x>4},
所以a>1,且方程(ax﹣x﹣b+1)(x+b)=0的两个根为x1=﹣1,x2=4,
则 或,解得或(舍去),
即有,即,解得.
所以不等式的解集为.
故选:C.
【点评】本题主要考查分式不等式的解法,属于基础题.
3.(5分)已知f(x),g(x)是定义域为R的函数,且f(x)是奇函数,g(x)是偶函数,满足f(x)+g(x)=ax2+x+2,若对任意的1<x1<x2<2,都有成立,则实数a的取值范围是
( )
A. B.
C. D.
【分析】根据奇偶函数构造方程组求出g(x)的解析式,再根据题意得到h(x)=ax2+3x+2在x∈(1,2)单调递增,分类讨论即可求解.
【解答】解:由题可得f(﹣x)+g(﹣x)=ax2﹣x+2,
因为f(x)是奇函数,g(x)是偶函数,
所以﹣f(x)+g(x)=ax2﹣x+2,
联立,解得g(x)=ax2+2,
又因为对任意的1<x1<x2<2,都有成立,
所以g(x1)﹣g(x2)<﹣3x1+3x2,所以g(x1)+3x1<g(x2)+3x2成立,
构造h(x)=g(x)+3x=ax2+3x+2,
所以由上述过程可得h(x)=ax2+3x+2在x∈(1,2)单调递增,
(i)若a<0,则对称轴,解得;
(ii) 若a=0,h(x)=3x+2在x∈(1,2)单调递增,满足题意;
(iii) 若a>0,则对称轴恒成立;
综上,,
故选:B.
【点评】本题考查函数性质的综合运用,考查运算求解能力,属于中档题.
4.(5分)若2024x﹣2024y<2025﹣x﹣2025﹣y,则( )
A.ln|x﹣y|>0 B.ln|x﹣y|<0
C.ln(y﹣x+1)>0 D.ln(y﹣x+1)<0
【分析】构造函数f(x)=2024x﹣2025﹣x,再利用函数单调性求解即可.
【解答】解:由2024x﹣2024y<2025﹣x﹣2025﹣y,
得2024x﹣2025﹣x<2024y﹣2025﹣y,
令f(x)=2024x﹣2025﹣x,
因为函数y=2024x,y=﹣2025﹣x都是增函数,
所以函数f(x)=2024x﹣2025﹣x是增函数,
由2024x﹣2025﹣x<2024y﹣2025﹣y,即f(x)<f(y),
所以x<y,
对于A、B:当x=1,y=2时,ln|x﹣y|=0,故A,B错误;
对于C、D:由x<y,得y﹣x+1>1,
所以ln(y﹣x+1)>0,故C正确,D错误.
故选:C.
【点评】本题考查函数的单调性,解题中转化思想的应用,属于中档题.
5.(5分)已知,为单位向量,且丄(+2),则向量与的夹角为( )
A.30° B.60° C.120° D.150°
【分析】根据题意,设向量与的夹角为θ,由向量垂直与向量数量积的关系分析可得若丄(+2),则 (+2)=2+2 =1+2cosθ=0,解可得cosθ的值,结合θ的范围,分析可得答案.
【解答】解:根据题意,设向量与的夹角为θ,
,为单位向量,则||=||=1,
若丄(+2),则 (+2)=2+2 =1+2cosθ=0,
解可得cosθ=﹣,
又由0°≤θ≤180°,
则θ=120°;
故选:C.
【点评】本题考查向量数量积的计算,关键是掌握向量垂直与向量数量积的关系.
6.(5分)若,则cos2A+cos2B的取值范围是( )
A. B. C. D.[0,1]
【分析】通过二倍角降幂公式化简,再利用和差化积公式以及将cos2A+cos2B,化简为,根据余弦函数的性质得出答案.
【解答】解:
=
=1+cos(A+B) cos(A﹣B),
∵,
∴
=,
∵,
∴,
故选:C.
【点评】本题主要考査的是三角函数中的二倍角以及和差化积公式的应用,属于中档题.
7.(5分)已知球O的表面积为16π,边长为3的等边△ABC的三个顶点都在球O的球面上,则三棱锥O﹣ABC的体积等于( )
A. B. C. D.
【分析】求出球的半径和△ABC所在平面截球所得的小圆的半径,利用勾股定理可得球心O到△ABC所在平面的距离,再利用棱锥的体积公式即可得解.
【解答】解:设球O的半径为R,则,解得R2=4,
设△ABC所在平面截球所得的小圆的半径为r,则,
故球心O到△ABC所在平面的距离为,即为三棱锥O﹣ABC的高,
所以.
故选:A.
【点评】本题主要考查棱锥的体积的求法,球的表面积公式,考查运算求解能力,属于基础题.
8.(5分)抛掷一颗骰子,设事件A:落地时向上的点数是奇数,事件B:落地时向上的点数是偶数,事件C:落地时向上的点数小于3,事件D:落地时向上的点数大于5,则下列每对事件中,不是互斥事件的是( )
A.A与B B.B与C C.A与D D.C与D
【分析】根据题意,由互斥事件的定义依次分析选项,综合可得答案.
【解答】解:根据题意,依次分析选项:
对于A,因为A与B不可能同时发生,所以事件A与B是互斥事件;
对于B,因为落地时向上的点数是偶数与落地时向上的点数小于3可能同时发生,如落地时向上的点数为2,
所以事件B与C不是互斥事件,所以B正确,
对于C,因为A与D不可能同时发生,所以事件A与D是互斥事件;
对于D,因为C与D不可能同时发生,所以事件C与D是互斥事件.
故选:B.
【点评】本题考查互斥事件的判断,注意互斥事件的定义,属于基础题.
二、多选题(本题共4小题,每小题5分,共20分)
(多选)9.(5分)有6个相同的球,分别标有数字1,2,3,4,5,6,从中不放回的随机取两次,每次取1个球,事件A表示“第一次取出的球的数字是偶数”,事件B表示“第二次取出的球的数字是奇数”,事件C表示“两次取出的球的数字之和是偶数”,事件D表示“两次取出的球的数字之和是奇数”,则( )
A.A与B是互斥事件 B.C与D互为对立事件
C.B发生的概率为 D.B与C相互独立
【分析】根据互斥事件,对立事件相互独立事件的定义结合古典概型注意判断即可.
【解答】解:由题意,不放回的随机取两次,共有6×6=36种情况,
A={(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),},共18个基本事件,
故,
B={(1,1),(2,1),(3,1),(4,1),(5,1),(6,1),
(1,3),(2,3),(3,3),(4,3),(5,3),(6,3),
(1,5),(2,5),(3,5),(4,5),(5,5),(6,5)},共18个基本事件,
故,故C正确;
则事件A与B不是互斥事件,故A错误;
C={(6,2),(6,4),(6,6),(5,1),(5,3),(5,5),
(4,2),(4,4),(4,6),(3,1),(3,3),(3,5),
(2,2),(2,4),(2,6),(1,1),(1,3),(1,5)},共18个基本事件,
故,
D={(1,2),(1,4),(1,6),(2,1),(2,3),(2,5),
(3,2),(3,4),(3,6),(4,1),(4,3),(4,5),
(5,2),(5,4),(5,6),(6,1),(6,3),(6,5)},共18个基本事件,
所以C与D互为对立事件,故B正确;
事件BC={(1,1),(3,1),(5,1),(1,3),(3,3),
(5,3),(1,5),(3,5),(5,5)},共9个基本事件,
所以,
所以B与C相互独立,故D正确.
故选:BCD.
【点评】本题主要互斥事件与对立时间,考查运算求解能力与逻辑推理能力,属于中档题.
(多选)10.(5分)如图,正方体ABCD﹣A1B1C1D1的棱长为2,则( )
A.BD∥平面CB1D1
B.AC1⊥平面CB1D1
C.异面直线CB1与BD所成的角为60°
D.三棱锥D﹣CB1D1的体积为
【分析】对A:借助正方体的性质可得BD∥B1D1,结合线面平行的判定定理即可得;对B:借助线面垂直的判定定理可得AD⊥平面C1D1DC,AA1⊥平面A1B1C1D1,再利用线面垂直的性质定理可得CD1⊥AD,AA1⊥B1D1,进而可得CD1⊥AC1,B1D1⊥AC1,即可得证;对C:借助等角定理可得∠CB1D1等于异面直线CB1与BD所成的角,计算出∠CB1D1即可得解;对D:借助体积公式计算即可得.
【解答】解:对A:在正方体ABCD﹣A1B1C1D1中,BD∥B1D1,
又B1D1 平面CB1D1,BD 平面CB1D1,所以BD∥平面CB1D1,故A项正确;
对B:连接A1C1,C1D,在正方体ABCD﹣A1B1C1D1中,B1D1⊥A1C1,DC1⊥CD1,
AD⊥平面C1D1DC,AA1⊥平面A1B1C1D1,因为CD1 平面C1D1DC,
B1D1 平面A1B1C1D1,所以CD1⊥AD,AA1⊥B1D1,
又DC1∩AD=D,DC1 平面AC1D,AD 平面AC1D,
所以CD1⊥平面AC1D,因此CD1⊥AC1,同理,B1D1⊥AC1,
又CD1∩B1D1=D1,CD1 平面CB1D1,B1D1 平面CB1D1,
所以AC1⊥平面CB1D1,故B项正确;
对C:因为B1D1∥BD,所以∠CB1D1等于异面直线CB1与BD所成的角,
又=,即△CB1D1为等边三角形,
所以异面直线CB1与BD所成的角为60°,故C项正确;
对D:三棱锥D﹣CB1D1的体积
=,故D项不正确.
故选:ABC.
【点评】本题以命题的真假判断为载体,考查了线面位置关系,考查了异面直线成角,考查了体积计算问题,属中档题.
(多选)11.(5分)已知α,β是两个不重合的平面,m,n是两条不重合的直线,则下列命题中是真命题的是( )
A.如果m⊥n,m⊥α,n∥β,那么α⊥β
B.如果m⊥α,n∥α,那么m⊥n
C.如果α∥β,m α,那么m∥β
D.如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等
【分析】根据空间直线与平面的位置关系的判定方法及几何特征,分析判断各个结论的真假,可得答案.
【解答】解:α,β是两个不重合的平面,m,n是两条不重合的直线,
对于A,可运用长方体举反例证明其错误,如图,
不妨设AA'为直线m,CD为直线n,四边形ABCD所在的平面为α,四边形ABC'D'所在的平面为β,
由图知这些直线和平面满足题目条件,但α⊥β不成立,故A错误;
对于B,设过直线n的某平面与平面α相交于直线l,则l∥n,由m⊥α,知m⊥l,从而m⊥n,故B正确;
对于C,由平面与平面平行的定义知,如果α∥β,m α,那么m∥β,故C正确;
对于D,由平行的传递性及线面角的定义知,
如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等,D正确.
故选:BCD.
【点评】本题以命题的真假判断与应用为载体,考查了空间直线与平面的位置关系等基础知识,考查空间想象能力,是中档题.
(多选)12.(5分)已知是函数f(x)=2asinxcosx﹣2cos2x﹣1的一个零点.则( )
A.a=
B.函数f(x)的值域为[﹣2,2]
C.函数f(x)的单调递减区间为,(k∈Z)
D.不等式f(x)≥0的解集为
【分析】由题意得f()=asin﹣cos﹣2=0,解得a的值,即可判断A;
化简函数解析式可得f(x)=2sin(2x﹣)﹣2,利用正弦函数的性质即可判断B;
利用正弦函数的单调性即可判断C;
令f(x)≥0,解得sin(2x﹣)≥1,解得x=+kπ,k∈Z,即可判断D.
【解答】解:由题意得f(x)=2asinxcosx﹣2cos2x﹣1=asin2x﹣cos2x﹣2,
因为是函数f(x)=2asinxcosx﹣2cos2x﹣1的一个零点,
所以f()=asin﹣cos﹣2=0,解得a=,故A正确;
因为f(x)=sin2x﹣cos2x﹣2=2sin(2x﹣)﹣2,
所以函数f(x)的值域为[﹣4,0],故B错误;
令+2kπ≤2x﹣≤+2kπ,k∈Z,解得+kπ≤x≤+kπ,k∈Z,
所以函数f(x)的单调递减区间为[+kπ,+kπ],k∈Z,故C正确;
令f(x)≥0,解得sin(2x﹣)≥1,
所以2x﹣=+2kπ,k∈Z,解得x=+kπ,k∈Z,
所以不等式f(x)≥0的解集为{x|x=+kπ,k∈Z},故D错误.
故选:AC.
【点评】本题考查二倍角公式、辅助角公式、正弦型函数的性质的应用,考查了函数思想,属于中档题.
三、填空题(本题共4小题,每小题5分,共20分)
13.(5分)甲、乙两水文站同时作水文预报,如果甲站、乙站各自预报的准确率分别为0.8和0.7,那么在一次预报中,甲站、乙站预报都错误的概率为 0.06 .
【分析】利用相互独立事件概率乘法公式求解.
【解答】解:因为甲站、乙站各自预报的准确率分别为0.8和0.7,
则在一次预报中,甲站、乙站预报都错误的概率为P=(1﹣0.8)×(1﹣0.7)=0.2×0.3=0.06.
故答案为:0.06.
【点评】本题考查相互独立事件概率乘法公式等基础知识,考查运算求解能力,是基础题.
14.(5分)已知a>0,b>0,且9a+b=ab,则a+4b的最小值为 49 .
【分析】由已知利用乘1法,结合基本不等式即可求解.
【解答】解:因为a>0,b>0,且9a+b=ab,
所以=1,
则a+4b=(a+4b)()=37+=49,
当且仅当a=7,b=时取等号,
所以a+4b的最小值为49.
故答案为:49.
【点评】本题考查基本不等式的运用,考查运算能力,属于基础题.
15.(5分)已知圆锥的顶点S和底面圆周都在球O的球面上,且母线长为2,A,B为其底面圆周上的两点,若△SAB面积的最大值为,则球O的表面积为 .
【分析】由三角形的面积公式和△SAB面积的最大值,推得圆锥的轴截面SPQ为等边三角形,求得底面半径,设球的半径为R,由勾股定理可得R的方程,即可得到所求表面积.
【解答】解:如图所示,因为,
所以当△SAB为轴截面时,∠ASB最大,
因为△SAB的面积最大值为,
则,所以,
即圆锥的轴截面SPQ为等边三角形,
因为圆锥的母线长为2,底面半径r=1,所以,
因为,
在直角△OPE中,OP2=OE2+PE2,
即,解得,
所以外接球表面积.
故答案为:.
【点评】本题主要考查球的表面积、三角形面积、圆锥的母线与轴截面等基础知识,考查运算求解、数
形结合的能力,属于中档题.
16.(5分)赵爽是我国古代数学家,大约在公元222年,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间一个小正方形组成).类比“赵爽弦图”,可构造如图所示的图形,它是由3个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形,设(λ,μ∈R),若DF=2AF,则= 3 .
【分析】因为大三角形是等边三角形,所以可以通过建系的方法进行求解.
【解答】解:不妨设AF=1,则AD=3,建系如图,由题可知.
在△ABD中,AD=3,BD=1,
由余弦定理可得,,
得,
所以,所以,,A(0,0),
在△ABD中,由正弦定理可得,
即为=,
解得,所以,
所以D(ADcos∠BAD,ADsin∠BAD),即.
所以,,,
因为,所以,
解得,所以.
故答案为:3.
【点评】本题考查三角形的余弦定理和平面向量基本定理,考查方程思想和运算能力,属于中档题.
四、解答题(本题共6小题,共70分)
17.(10分)甲袋子中装有2个红球、1个白球,乙袋子中装有1个红球、2个白球(袋子不透明,球除颜色外完全一样).
(1)现从甲、乙两个袋子中各任选1个球,求选出的2个球的颜色相同的概率;
(2)从甲、乙两袋6个球中任选2个球,求选出的2个球来自同一袋子的概率.
【分析】(1)直接由列举法求解古典概型概率即可;
(2)直接由列举法求解古典概型概率即可.
【解答】解:(1)根据题意,甲袋子中2个红球分别用A,B表示,白球用C表示,乙袋子中红球用D表示,2个白球分别用E,F表示.
从甲、乙两袋中各任选1个球的所有可能结果为(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),共9种,
从中选出的2个球的颜色相同的有(A,D),(B,D),(C,E),(C,F),共4种,
故选出的2个球的颜色相同的概率.
(2)从6个球中任选2个球的所有可能结果为
(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种,
从中选出2个球来自同一袋子的结果有(A,B),(A,C),(B,C),(D,E),(D,F),(E,F),共6种,
所以选出的2个球来自同一袋子的概率.
【点评】本题考查古典概型的计算,注意列举法的应用,属于基础题.
18.(12分)如图,四棱锥P﹣ABCD的底面ABCD是直角梯形,PA⊥底面ABCD,AB∥CD,CD⊥BC,且.
(1)证明:平面PBC⊥平面PAB.
(2)求二面角A﹣BC﹣P的大小.
【分析】(1)由题意可得PA⊥BC,AB⊥BC,可证平面PBC⊥平面PAB.
(2)由(1)可知BC⊥PB,BC⊥BA,可得∠PBA为二面角A﹣BC﹣P的平面角,进而求解即可.
【解答】解:(1)证明:∵PA⊥平面ABCD,BC 平面ABCD,∴PA⊥BC,
又AB∥CD,CD⊥BC,∴AB⊥BC,PA∩AB=A,∴BC⊥平面PAB,
∵BC 平面PBC,∴平面PBC⊥平面PAB.
(2)由(1)可知BC⊥PB,BC⊥BA,
∴∠PBA为二面角A﹣BC﹣P的平面角,
过D作DE∥BC交AB于点E,
又AB∥CD,CD⊥BC,∴四边形BCDE为矩形,
∴DE=BC=,BE=CD,
又AB=AD=2CD,∴EA=AD,∴∠ADE=30°,
∴AE=DE,∴AE=1,∴AB=2,
∵PA=2,
在Rt△PAB中,tan∠PBA===,
∴∠PBA=60°,
∴二面角A﹣BC﹣P的大小为60°.
【点评】本题考查面面垂直的证明,考查二面角的大小的求法,属中档题.
19.(12分)黄山原名“黟山”,因峰岩青黑,遥望苍黛而名,后因传说轩辕黄帝曾在此炼丹,故改名为“黄山”.黄山雄踞风景秀丽的安徽南部,是我国最著名的山岳风景区之一.明代旅行家、地理学家徐霞客两游黄山,赞叹说:“登黄山天下无山,观止矣!”又留“五岳归来不看山,黄山归来不看岳”的美誉.为更好地提升旅游品质,黄山风景区的工作人员随机选择100名游客对景区进行满意度评分(满分100分),根据评分,制成如图所示的频率分布直方图.
(1)根据频率分布直方图,求x的值;
(2)估计这100名游客对景区满意度评分的40%分位数(得数保留两位小数);
(3)景区的工作人员采用按比例分层抽样的方法从评分在[50,60),[60,70)的两组中共抽取6人,再从这6人中随机抽取2人进行个别交流,求选取的2人评分分别在[50,60)和[60,70)内各1人的概率.
【分析】(1)根据直方科中频率和为1,能求出结果.
(2)由百分位数的定义,结合频率分布直方图能求出结果.
(3)分别求出各组人数,利用列举法结合古典概型求解.
【解答】解:(1)由频率分布直方图得:
10(0.005+0.01+0.015+x+0.04)=1,
解得x=0.03.
(2)由10(0.005+0.01+0.015)=0.3<0.4<10(0.005+0.01+0.015+0.03)=0.6,
∴40%分位数在区间[80,90)内,令其为m,
则0.3+0.03×(m﹣80)=0.4,
解得m=80+≈83.33,
∴这100名游客对景区满意度评分的40%分位数为83.33分.
(3)∵评分在[50,60),[60,70)的频率分别为0.05,0.1,
则在[50,60)中抽取=2人,设为a,b,
在[60,70)中抽取人,设为C,D,E,F,
从这6人中随机抽取2人,基本事件有:
{a,b},{a,C},{a,D},{a,E},{a,F},{b,C},{b,D},{b,E},{b,F},{C,D},{C,E},C,F},{D,E},{D,F},{E,F},共15个,
设事件A表示”选取的2人评分分别在[50,60)和[60,70)内各1人“,
则事件A包含的基本事件有:
{a,C},{a,D},{a,E},{a,F},{b,C},{b,D},{b,E},{b,F},共8个,
∴选取的2人评分分别在[50,60)和[60,70)内各1人的概率为P==.
【点评】本题考查频率分布直方图、中位数、列举法、古典概型等基础知识,考查运算求解能力,是基础题.
20.(12分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的图象如图所示.将函数y=f(x)的图象向右平移个单位长度得到曲线C,把C上各点的横坐标伸长到原来的2倍,纵坐标不变,得到的曲线对应的函数记作y=g(x).
(1)求函数f(x)的单调减区间;
(2)求函数的最小值;
(3)若函数在(0,4π)内恰有6个零点,求m的值.
【分析】(1)根据所给图象求出函数f(x)的解析式,再列出关于x的不等式即可得解;
(2)由(1)结合给定图象变换求出g(x)的解析式,再求出h(x)并作变形即可得解;
(3)求出F(x)并令t=sinx,将F(x)=0转化为关于t的一元二次方程,按根所在区间讨论得解.
【解答】解:(1)观察图象得A=1,f(x)最小正周期为T,
则,则,
而,则+φ=+2kπ,k∈Z,
解得,k∈Z,
又,于是得,
所以,
函数的单调递减区间满足:,k∈Z,
得,k∈Z,
所以单调递减区间为,k∈Z;
(2)将函数y=f(x)的图象向右平移个单位长度得到曲线C,即y=sin[2(x﹣)+]=sin2x,
再把C上各点的横坐标伸长到原来的2倍,纵坐标不变,得到的曲线对应的函数记作y=g(x),
即g(x)=sinx,
所以h(x)=f()g(x)=sin(x+)sinx=(sinx+cosx)sinx
=sin2x+sinxcosx=+sin2x
=(sin2x﹣cos2x)+
=sin(2x﹣)+,
当时,函数确定最小值,即时,h(x)min=×(﹣1)+=﹣,
所以的最小值为﹣;
(3)依题意,m∈R,
令F(x)=0,可得2sin2x﹣msinx﹣1=0,
令t=sinx∈[﹣1,1],得2t2﹣mt﹣1=0,
由于Δ=m2+8>0,即方程必有两个不同的实数根t1,t2,
且,,
由知t1、t2异号,不妨设t1>0,t2<0,
①若t1>1,则,sinx=t1,无解,
而sinx=t2在(0,4π)内有四个零点,不符题意;
②若t1=1,则,sinx=1在(0,4π)内有2个零点,
而在(0,4π)内有4个零点,
即F(x)在(0,4π)内有6个零点,符合题意,
此时,得m=1;
③若0<t1<1,,sinx=t1在(0,4π)有4个零点,
则sinx=t2在(0,4π)内应恰有2个零点,必有t2=﹣1,
此时,,解得m=﹣1,
综上所述有m=1或m=﹣1.
【点评】本题考查三角函数的图象与性质以及函数零点的综合应用,属中档题.
21.(12分)如图,平面四边形ABCD中,AB=8,CD=3,,∠ADC=90°,∠BAD=30°,点E,F满足,,将△AEF沿EF翻折至△PEF,使得.
(1)证明:EF⊥PD;
(2)求五棱锥P﹣BCDEF的体积.
【分析】(1)先用勾股定理证明AE⊥EF,再证明EF⊥面PED即可;
(2)先证明PE为锥体的高,再用锥体的体积公式即可求解.
【解答】解:(1)证明:由AB=8,,,则AE=2,,则AF=4,
在△AEF中,∠BAD=30°,由余弦定理得,
所以AE2+EF2=AF2,则AE⊥EF,即EF⊥AD,
所以EF⊥PE,EF⊥DE,又PE∩DE=E,所以EF⊥平面PDE,
又PD 平面PDE,故EF⊥PD;
(2)因为CD⊥AD,EF⊥AD,所以CD∥EF,即CD⊥平面PED,
所以CD⊥PD,,
又,,所以PE2+ED2=PD2,所以PE⊥ED,由此得PE⊥底面BCDEF,PE即为五棱锥的高,
过B点作BG∥EF.则BG=2EF=4,
S底=S梯形EFBG+S梯形CDGB=×(2+4)×2+×(3+4)×=,
V=×S底×PE=××2=19.
【点评】本题考查线面垂直的判定定理以及性质定理,锥体的体积公式,属于中档题.
22.(12分)某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25米,为了便于游客休闲散步,该农庄决定在鱼塘内建三条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°.
(1)设∠BOE=α,试将△OEF的周长l表示成α的函数关系式,并求出此函数的定义域;
(2)经核算,三条走廊每米建设费用均为4000元,试问如何设计才能使建设总费用最低并求出最低总费用.
【分析】(1)要将△OEF的周长l表示成α的函数关系式,需把△OEF的三边分别用含有α的关系式来表示,而OE,
OF,分别可以在Rt△OBE,Rt△OAF中求解,利用勾股定理可求EF,从而可求.
(2)要求铺路总费用最低,只要求△OEF的周长l的最小值即可.由(1)得l=,α∈[,],
利用换元,设sinα+cosα=t,则sinαcosα=,从而转化为求函数在闭区间上的最小值.
【解答】解:(1)∵在Rt△BOE中,OB=25,∠B=90°,∠BOE=α,
∴OE=
在Rt△AOF中,OA=25,∠A=90°,∠AFO=α,
∴OF=.
又∠EOF=90°,
∴EF==,
∴l=OE+OF+EF=.
当点F在点D时,这时角α最小,此时α=;
当点E在C点时,这时角α最大,求得此时α=.
故此函数的定义域为[,];
(2)由题意知,要求铺路总费用最低,只要求△OEF的周长l的最小值即可.
由(1)得,l=,α∈[,],
设sinα+cosα=t,则sinαcosα=,
∴l==
由t=sinα+cosα=sin(α+),
又≤α+≤,得,
∴,
从而当α=,即BE=25时,lmin=50(+1),
所以当BE=AF=25米时,铺路总费用最低,最低总费用为200000(+1)元.
【点评】本题主要考查了借助于三角函数解三角形在实际问题中的应用,考查了利用数学知识解决实际问题的能力,及推理运算的能力.
一、单选题(本题共8小题,每小题5分,共40分)
1.(5分)如果集合S={x|x=3n+1,n∈N},T={x|x=3k﹣2,k∈Z},则( )
A.S T B.T S C.S=T D.S T
2.(5分)不等式的解集为{x|x<﹣1或x>4},则的解集为( )
A. B.{x|﹣1≤x<1}
C. D.
3.(5分)已知f(x),g(x)是定义域为R的函数,且f(x)是奇函数,g(x)是偶函数,满足f(x)+g(x)=ax2+x+2,若对任意的1<x1<x2<2,都有成立,则实数a的取值范围是( )
A. B.
C. D.
4.(5分)若2024x﹣2024y<2025﹣x﹣2025﹣y,则( )
A.ln|x﹣y|>0 B.ln|x﹣y|<0
C.ln(y﹣x+1)>0 D.ln(y﹣x+1)<0
5.(5分)已知,为单位向量,且丄(+2),则向量与的夹角为( )
A.30° B.60° C.120° D.150°
6.(5分)若,则cos2A+cos2B的取值范围是( )
A. B. C. D.[0,1]
7.(5分)已知球O的表面积为16π,边长为3的等边△ABC的三个顶点都在球O的球面上,则三棱锥O﹣ABC的体积等于( )
A. B. C. D.
8.(5分)抛掷一颗骰子,设事件A:落地时向上的点数是奇数,事件B:落地时向上的点数是偶数,事件C:落地时向上的点数小于3,事件D:落地时向上的点数大于5,则下列每对事件中,不是互斥事件的是( )
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
A.A与B B.B与C C.A与D D.C与D
二、多选题(本题共4小题,每小题5分,共20分)
(多选)9.(5分)有6个相同的球,分别标有数字1,2,3,4,5,6,从中不放回的随机取两次,每次取1个球,事件A表示“第一次取出的球的数字是偶数”,事件B表示“第二次取出的球的数字是奇数”,事件C表示“两次取出的球的数字之和是偶数”,事件D表示“两次取出的球的数字之和是奇数”,则( )
A.A与B是互斥事件 B.C与D互为对立事件
C.B发生的概率为 D.B与C相互独立
(多选)10.(5分)如图,正方体ABCD﹣A1B1C1D1的棱长为2,则( )
A.BD∥平面CB1D1
B.AC1⊥平面CB1D1
C.异面直线CB1与BD所成的角为60°
D.三棱锥D﹣CB1D1的体积为
(多选)11.(5分)已知α,β是两个不重合的平面,m,n是两条不重合的直线,则下列命题中是真命题的是( )
A.如果m⊥n,m⊥α,n∥β,那么α⊥β
B.如果m⊥α,n∥α,那么m⊥n
C.如果α∥β,m α,那么m∥β
D.如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等
(多选)12.(5分)已知是函数f(x)=2asinxcosx﹣2cos2x﹣1的一个零点.则( )
A.a=
B.函数f(x)的值域为[﹣2,2]
C.函数f(x)的单调递减区间为,(k∈Z)
D.不等式f(x)≥0的解集为
三、填空题(本题共4小题,每小题5分,共20分)
13.(5分)甲、乙两水文站同时作水文预报,如果甲站、乙站各自预报的准确率分别为0.8和0.7,那么在一次预报中,甲站、乙站预报都错误的概率为 .
14.(5分)已知a>0,b>0,且9a+b=ab,则a+4b的最小值为 .
15.(5分)已知圆锥的顶点S和底面圆周都在球O的球面上,且母线长为2,A,B为其底面圆周上的两点,若△SAB面积的最大值为,则球O的表面积为 .
16.(5分)赵爽是我国古代数学家,大约在公元222年,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间一个小正方形组成).类比“赵爽弦图”,可构造如图所示的图形,它是由3个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形,设(λ,μ∈R),若DF=2AF,则= .
四、解答题(本题共6小题,共70分)
17.(10分)甲袋子中装有2个红球、1个白球,乙袋子中装有1个红球、2个白球(袋子不透明,球除颜色外完全一样).
(1)现从甲、乙两个袋子中各任选1个球,求选出的2个球的颜色相同的概率;
(2)从甲、乙两袋6个球中任选2个球,求选出的2个球来自同一袋子的概率.
18.(12分)如图,四棱锥P﹣ABCD的底面ABCD是直角梯形,PA⊥底面ABCD,AB∥CD,CD⊥BC,且.
(1)证明:平面PBC⊥平面PAB.
(2)求二面角A﹣BC﹣P的大小.
19.(12分)黄山原名“黟山”,因峰岩青黑,遥望苍黛而名,后因传说轩辕黄帝曾在此炼丹,故改名为“黄山”.黄山雄踞风景秀丽的安徽南部,是我国最著名的山岳风景区之一.明代旅行家、地理学家徐霞客两游黄山,赞叹说:“登黄山天下无山,观止矣!”又留“五岳归来不看山,黄山归来不看岳”的美誉.为更好地提升旅游品质,黄山风景区的工作人员随机选择100名游客对景区进行满意度评分(满分100分),根据评分,制成如图所示的频率分布直方图.
(1)根据频率分布直方图,求x的值;
(2)估计这100名游客对景区满意度评分的40%分位数(得数保留两位小数);
(3)景区的工作人员采用按比例分层抽样的方法从评分在[50,60),[60,70)的两组中共抽取6人,再从这6人中随机抽取2人进行个别交流,求选取的2人评分分别在[50,60)和[60,70)内各1人的概率.
20.(12分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的图象如图所示.将函数y=f(x)的图象向右平移个单位长度得到曲线C,把C上各点的横坐标伸长到原来的2倍,纵坐标不变,得到的曲线对应的函数记作y=g(x).
(1)求函数f(x)的单调减区间;
(2)求函数的最小值;
(3)若函数在(0,4π)内恰有6个零点,求m的值.
21.(12分)如图,平面四边形ABCD中,AB=8,CD=3,,∠ADC=90°,∠BAD=30°,点E,F满足,,将△AEF沿EF翻折至△PEF,使得.
(1)证明:EF⊥PD;
(2)求五棱锥P﹣BCDEF的体积.
22.(12分)某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25米,为了便于游客休闲散步,该农庄决定在鱼塘内建三条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°.
(1)设∠BOE=α,试将△OEF的周长l表示成α的函数关系式,并求出此函数的定义域;
(2)经核算,三条走廊每米建设费用均为4000元,试问如何设计才能使建设总费用最低并求出最低总费用.
参考答案与试题解析
一、单选题(本题共8小题,每小题5分,共40分)
1.(5分)如果集合S={x|x=3n+1,n∈N},T={x|x=3k﹣2,k∈Z},则( )
A.S T B.T S C.S=T D.S T
【分析】由S={x|x=3n+1,n∈N},T={x|x=3k﹣2,k∈+1,k∈Z},即可判断S和T的关系.
【解答】解:S={x|x=3n+1,n∈N},T={x|x=3k﹣2,k∈+1,k∈Z},
故S T,只有A正确.
故选:A.
【点评】本题考查集合与集合的关系的判断,属于基础题.
2.(5分)不等式的解集为{x|x<﹣1或x>4},则的解集为( )
A. B.{x|﹣1≤x<1} C. D.
【分析】将不等式化为(ax﹣x﹣b+1)(x+b)>0,即(ax﹣x﹣b+1)(x+b)=0的两个根为x1=﹣1,x2=4,代入求出a,b,再利用分式不等式的解法即可求解.
【解答】解:不等式可转化为[(a﹣1)x﹣b+1](x+b)>0,
其解集为{x|x<﹣1或x>4},
所以a>1,且方程(ax﹣x﹣b+1)(x+b)=0的两个根为x1=﹣1,x2=4,
则 或,解得或(舍去),
即有,即,解得.
所以不等式的解集为.
故选:C.
【点评】本题主要考查分式不等式的解法,属于基础题.
3.(5分)已知f(x),g(x)是定义域为R的函数,且f(x)是奇函数,g(x)是偶函数,满足f(x)+g(x)=ax2+x+2,若对任意的1<x1<x2<2,都有成立,则实数a的取值范围是
( )
A. B.
C. D.
【分析】根据奇偶函数构造方程组求出g(x)的解析式,再根据题意得到h(x)=ax2+3x+2在x∈(1,2)单调递增,分类讨论即可求解.
【解答】解:由题可得f(﹣x)+g(﹣x)=ax2﹣x+2,
因为f(x)是奇函数,g(x)是偶函数,
所以﹣f(x)+g(x)=ax2﹣x+2,
联立,解得g(x)=ax2+2,
又因为对任意的1<x1<x2<2,都有成立,
所以g(x1)﹣g(x2)<﹣3x1+3x2,所以g(x1)+3x1<g(x2)+3x2成立,
构造h(x)=g(x)+3x=ax2+3x+2,
所以由上述过程可得h(x)=ax2+3x+2在x∈(1,2)单调递增,
(i)若a<0,则对称轴,解得;
(ii) 若a=0,h(x)=3x+2在x∈(1,2)单调递增,满足题意;
(iii) 若a>0,则对称轴恒成立;
综上,,
故选:B.
【点评】本题考查函数性质的综合运用,考查运算求解能力,属于中档题.
4.(5分)若2024x﹣2024y<2025﹣x﹣2025﹣y,则( )
A.ln|x﹣y|>0 B.ln|x﹣y|<0
C.ln(y﹣x+1)>0 D.ln(y﹣x+1)<0
【分析】构造函数f(x)=2024x﹣2025﹣x,再利用函数单调性求解即可.
【解答】解:由2024x﹣2024y<2025﹣x﹣2025﹣y,
得2024x﹣2025﹣x<2024y﹣2025﹣y,
令f(x)=2024x﹣2025﹣x,
因为函数y=2024x,y=﹣2025﹣x都是增函数,
所以函数f(x)=2024x﹣2025﹣x是增函数,
由2024x﹣2025﹣x<2024y﹣2025﹣y,即f(x)<f(y),
所以x<y,
对于A、B:当x=1,y=2时,ln|x﹣y|=0,故A,B错误;
对于C、D:由x<y,得y﹣x+1>1,
所以ln(y﹣x+1)>0,故C正确,D错误.
故选:C.
【点评】本题考查函数的单调性,解题中转化思想的应用,属于中档题.
5.(5分)已知,为单位向量,且丄(+2),则向量与的夹角为( )
A.30° B.60° C.120° D.150°
【分析】根据题意,设向量与的夹角为θ,由向量垂直与向量数量积的关系分析可得若丄(+2),则 (+2)=2+2 =1+2cosθ=0,解可得cosθ的值,结合θ的范围,分析可得答案.
【解答】解:根据题意,设向量与的夹角为θ,
,为单位向量,则||=||=1,
若丄(+2),则 (+2)=2+2 =1+2cosθ=0,
解可得cosθ=﹣,
又由0°≤θ≤180°,
则θ=120°;
故选:C.
【点评】本题考查向量数量积的计算,关键是掌握向量垂直与向量数量积的关系.
6.(5分)若,则cos2A+cos2B的取值范围是( )
A. B. C. D.[0,1]
【分析】通过二倍角降幂公式化简,再利用和差化积公式以及将cos2A+cos2B,化简为,根据余弦函数的性质得出答案.
【解答】解:
=
=1+cos(A+B) cos(A﹣B),
∵,
∴
=,
∵,
∴,
故选:C.
【点评】本题主要考査的是三角函数中的二倍角以及和差化积公式的应用,属于中档题.
7.(5分)已知球O的表面积为16π,边长为3的等边△ABC的三个顶点都在球O的球面上,则三棱锥O﹣ABC的体积等于( )
A. B. C. D.
【分析】求出球的半径和△ABC所在平面截球所得的小圆的半径,利用勾股定理可得球心O到△ABC所在平面的距离,再利用棱锥的体积公式即可得解.
【解答】解:设球O的半径为R,则,解得R2=4,
设△ABC所在平面截球所得的小圆的半径为r,则,
故球心O到△ABC所在平面的距离为,即为三棱锥O﹣ABC的高,
所以.
故选:A.
【点评】本题主要考查棱锥的体积的求法,球的表面积公式,考查运算求解能力,属于基础题.
8.(5分)抛掷一颗骰子,设事件A:落地时向上的点数是奇数,事件B:落地时向上的点数是偶数,事件C:落地时向上的点数小于3,事件D:落地时向上的点数大于5,则下列每对事件中,不是互斥事件的是( )
A.A与B B.B与C C.A与D D.C与D
【分析】根据题意,由互斥事件的定义依次分析选项,综合可得答案.
【解答】解:根据题意,依次分析选项:
对于A,因为A与B不可能同时发生,所以事件A与B是互斥事件;
对于B,因为落地时向上的点数是偶数与落地时向上的点数小于3可能同时发生,如落地时向上的点数为2,
所以事件B与C不是互斥事件,所以B正确,
对于C,因为A与D不可能同时发生,所以事件A与D是互斥事件;
对于D,因为C与D不可能同时发生,所以事件C与D是互斥事件.
故选:B.
【点评】本题考查互斥事件的判断,注意互斥事件的定义,属于基础题.
二、多选题(本题共4小题,每小题5分,共20分)
(多选)9.(5分)有6个相同的球,分别标有数字1,2,3,4,5,6,从中不放回的随机取两次,每次取1个球,事件A表示“第一次取出的球的数字是偶数”,事件B表示“第二次取出的球的数字是奇数”,事件C表示“两次取出的球的数字之和是偶数”,事件D表示“两次取出的球的数字之和是奇数”,则( )
A.A与B是互斥事件 B.C与D互为对立事件
C.B发生的概率为 D.B与C相互独立
【分析】根据互斥事件,对立事件相互独立事件的定义结合古典概型注意判断即可.
【解答】解:由题意,不放回的随机取两次,共有6×6=36种情况,
A={(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),},共18个基本事件,
故,
B={(1,1),(2,1),(3,1),(4,1),(5,1),(6,1),
(1,3),(2,3),(3,3),(4,3),(5,3),(6,3),
(1,5),(2,5),(3,5),(4,5),(5,5),(6,5)},共18个基本事件,
故,故C正确;
则事件A与B不是互斥事件,故A错误;
C={(6,2),(6,4),(6,6),(5,1),(5,3),(5,5),
(4,2),(4,4),(4,6),(3,1),(3,3),(3,5),
(2,2),(2,4),(2,6),(1,1),(1,3),(1,5)},共18个基本事件,
故,
D={(1,2),(1,4),(1,6),(2,1),(2,3),(2,5),
(3,2),(3,4),(3,6),(4,1),(4,3),(4,5),
(5,2),(5,4),(5,6),(6,1),(6,3),(6,5)},共18个基本事件,
所以C与D互为对立事件,故B正确;
事件BC={(1,1),(3,1),(5,1),(1,3),(3,3),
(5,3),(1,5),(3,5),(5,5)},共9个基本事件,
所以,
所以B与C相互独立,故D正确.
故选:BCD.
【点评】本题主要互斥事件与对立时间,考查运算求解能力与逻辑推理能力,属于中档题.
(多选)10.(5分)如图,正方体ABCD﹣A1B1C1D1的棱长为2,则( )
A.BD∥平面CB1D1
B.AC1⊥平面CB1D1
C.异面直线CB1与BD所成的角为60°
D.三棱锥D﹣CB1D1的体积为
【分析】对A:借助正方体的性质可得BD∥B1D1,结合线面平行的判定定理即可得;对B:借助线面垂直的判定定理可得AD⊥平面C1D1DC,AA1⊥平面A1B1C1D1,再利用线面垂直的性质定理可得CD1⊥AD,AA1⊥B1D1,进而可得CD1⊥AC1,B1D1⊥AC1,即可得证;对C:借助等角定理可得∠CB1D1等于异面直线CB1与BD所成的角,计算出∠CB1D1即可得解;对D:借助体积公式计算即可得.
【解答】解:对A:在正方体ABCD﹣A1B1C1D1中,BD∥B1D1,
又B1D1 平面CB1D1,BD 平面CB1D1,所以BD∥平面CB1D1,故A项正确;
对B:连接A1C1,C1D,在正方体ABCD﹣A1B1C1D1中,B1D1⊥A1C1,DC1⊥CD1,
AD⊥平面C1D1DC,AA1⊥平面A1B1C1D1,因为CD1 平面C1D1DC,
B1D1 平面A1B1C1D1,所以CD1⊥AD,AA1⊥B1D1,
又DC1∩AD=D,DC1 平面AC1D,AD 平面AC1D,
所以CD1⊥平面AC1D,因此CD1⊥AC1,同理,B1D1⊥AC1,
又CD1∩B1D1=D1,CD1 平面CB1D1,B1D1 平面CB1D1,
所以AC1⊥平面CB1D1,故B项正确;
对C:因为B1D1∥BD,所以∠CB1D1等于异面直线CB1与BD所成的角,
又=,即△CB1D1为等边三角形,
所以异面直线CB1与BD所成的角为60°,故C项正确;
对D:三棱锥D﹣CB1D1的体积
=,故D项不正确.
故选:ABC.
【点评】本题以命题的真假判断为载体,考查了线面位置关系,考查了异面直线成角,考查了体积计算问题,属中档题.
(多选)11.(5分)已知α,β是两个不重合的平面,m,n是两条不重合的直线,则下列命题中是真命题的是( )
A.如果m⊥n,m⊥α,n∥β,那么α⊥β
B.如果m⊥α,n∥α,那么m⊥n
C.如果α∥β,m α,那么m∥β
D.如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等
【分析】根据空间直线与平面的位置关系的判定方法及几何特征,分析判断各个结论的真假,可得答案.
【解答】解:α,β是两个不重合的平面,m,n是两条不重合的直线,
对于A,可运用长方体举反例证明其错误,如图,
不妨设AA'为直线m,CD为直线n,四边形ABCD所在的平面为α,四边形ABC'D'所在的平面为β,
由图知这些直线和平面满足题目条件,但α⊥β不成立,故A错误;
对于B,设过直线n的某平面与平面α相交于直线l,则l∥n,由m⊥α,知m⊥l,从而m⊥n,故B正确;
对于C,由平面与平面平行的定义知,如果α∥β,m α,那么m∥β,故C正确;
对于D,由平行的传递性及线面角的定义知,
如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等,D正确.
故选:BCD.
【点评】本题以命题的真假判断与应用为载体,考查了空间直线与平面的位置关系等基础知识,考查空间想象能力,是中档题.
(多选)12.(5分)已知是函数f(x)=2asinxcosx﹣2cos2x﹣1的一个零点.则( )
A.a=
B.函数f(x)的值域为[﹣2,2]
C.函数f(x)的单调递减区间为,(k∈Z)
D.不等式f(x)≥0的解集为
【分析】由题意得f()=asin﹣cos﹣2=0,解得a的值,即可判断A;
化简函数解析式可得f(x)=2sin(2x﹣)﹣2,利用正弦函数的性质即可判断B;
利用正弦函数的单调性即可判断C;
令f(x)≥0,解得sin(2x﹣)≥1,解得x=+kπ,k∈Z,即可判断D.
【解答】解:由题意得f(x)=2asinxcosx﹣2cos2x﹣1=asin2x﹣cos2x﹣2,
因为是函数f(x)=2asinxcosx﹣2cos2x﹣1的一个零点,
所以f()=asin﹣cos﹣2=0,解得a=,故A正确;
因为f(x)=sin2x﹣cos2x﹣2=2sin(2x﹣)﹣2,
所以函数f(x)的值域为[﹣4,0],故B错误;
令+2kπ≤2x﹣≤+2kπ,k∈Z,解得+kπ≤x≤+kπ,k∈Z,
所以函数f(x)的单调递减区间为[+kπ,+kπ],k∈Z,故C正确;
令f(x)≥0,解得sin(2x﹣)≥1,
所以2x﹣=+2kπ,k∈Z,解得x=+kπ,k∈Z,
所以不等式f(x)≥0的解集为{x|x=+kπ,k∈Z},故D错误.
故选:AC.
【点评】本题考查二倍角公式、辅助角公式、正弦型函数的性质的应用,考查了函数思想,属于中档题.
三、填空题(本题共4小题,每小题5分,共20分)
13.(5分)甲、乙两水文站同时作水文预报,如果甲站、乙站各自预报的准确率分别为0.8和0.7,那么在一次预报中,甲站、乙站预报都错误的概率为 0.06 .
【分析】利用相互独立事件概率乘法公式求解.
【解答】解:因为甲站、乙站各自预报的准确率分别为0.8和0.7,
则在一次预报中,甲站、乙站预报都错误的概率为P=(1﹣0.8)×(1﹣0.7)=0.2×0.3=0.06.
故答案为:0.06.
【点评】本题考查相互独立事件概率乘法公式等基础知识,考查运算求解能力,是基础题.
14.(5分)已知a>0,b>0,且9a+b=ab,则a+4b的最小值为 49 .
【分析】由已知利用乘1法,结合基本不等式即可求解.
【解答】解:因为a>0,b>0,且9a+b=ab,
所以=1,
则a+4b=(a+4b)()=37+=49,
当且仅当a=7,b=时取等号,
所以a+4b的最小值为49.
故答案为:49.
【点评】本题考查基本不等式的运用,考查运算能力,属于基础题.
15.(5分)已知圆锥的顶点S和底面圆周都在球O的球面上,且母线长为2,A,B为其底面圆周上的两点,若△SAB面积的最大值为,则球O的表面积为 .
【分析】由三角形的面积公式和△SAB面积的最大值,推得圆锥的轴截面SPQ为等边三角形,求得底面半径,设球的半径为R,由勾股定理可得R的方程,即可得到所求表面积.
【解答】解:如图所示,因为,
所以当△SAB为轴截面时,∠ASB最大,
因为△SAB的面积最大值为,
则,所以,
即圆锥的轴截面SPQ为等边三角形,
因为圆锥的母线长为2,底面半径r=1,所以,
因为,
在直角△OPE中,OP2=OE2+PE2,
即,解得,
所以外接球表面积.
故答案为:.
【点评】本题主要考查球的表面积、三角形面积、圆锥的母线与轴截面等基础知识,考查运算求解、数
形结合的能力,属于中档题.
16.(5分)赵爽是我国古代数学家,大约在公元222年,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间一个小正方形组成).类比“赵爽弦图”,可构造如图所示的图形,它是由3个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形,设(λ,μ∈R),若DF=2AF,则= 3 .
【分析】因为大三角形是等边三角形,所以可以通过建系的方法进行求解.
【解答】解:不妨设AF=1,则AD=3,建系如图,由题可知.
在△ABD中,AD=3,BD=1,
由余弦定理可得,,
得,
所以,所以,,A(0,0),
在△ABD中,由正弦定理可得,
即为=,
解得,所以,
所以D(ADcos∠BAD,ADsin∠BAD),即.
所以,,,
因为,所以,
解得,所以.
故答案为:3.
【点评】本题考查三角形的余弦定理和平面向量基本定理,考查方程思想和运算能力,属于中档题.
四、解答题(本题共6小题,共70分)
17.(10分)甲袋子中装有2个红球、1个白球,乙袋子中装有1个红球、2个白球(袋子不透明,球除颜色外完全一样).
(1)现从甲、乙两个袋子中各任选1个球,求选出的2个球的颜色相同的概率;
(2)从甲、乙两袋6个球中任选2个球,求选出的2个球来自同一袋子的概率.
【分析】(1)直接由列举法求解古典概型概率即可;
(2)直接由列举法求解古典概型概率即可.
【解答】解:(1)根据题意,甲袋子中2个红球分别用A,B表示,白球用C表示,乙袋子中红球用D表示,2个白球分别用E,F表示.
从甲、乙两袋中各任选1个球的所有可能结果为(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),共9种,
从中选出的2个球的颜色相同的有(A,D),(B,D),(C,E),(C,F),共4种,
故选出的2个球的颜色相同的概率.
(2)从6个球中任选2个球的所有可能结果为
(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种,
从中选出2个球来自同一袋子的结果有(A,B),(A,C),(B,C),(D,E),(D,F),(E,F),共6种,
所以选出的2个球来自同一袋子的概率.
【点评】本题考查古典概型的计算,注意列举法的应用,属于基础题.
18.(12分)如图,四棱锥P﹣ABCD的底面ABCD是直角梯形,PA⊥底面ABCD,AB∥CD,CD⊥BC,且.
(1)证明:平面PBC⊥平面PAB.
(2)求二面角A﹣BC﹣P的大小.
【分析】(1)由题意可得PA⊥BC,AB⊥BC,可证平面PBC⊥平面PAB.
(2)由(1)可知BC⊥PB,BC⊥BA,可得∠PBA为二面角A﹣BC﹣P的平面角,进而求解即可.
【解答】解:(1)证明:∵PA⊥平面ABCD,BC 平面ABCD,∴PA⊥BC,
又AB∥CD,CD⊥BC,∴AB⊥BC,PA∩AB=A,∴BC⊥平面PAB,
∵BC 平面PBC,∴平面PBC⊥平面PAB.
(2)由(1)可知BC⊥PB,BC⊥BA,
∴∠PBA为二面角A﹣BC﹣P的平面角,
过D作DE∥BC交AB于点E,
又AB∥CD,CD⊥BC,∴四边形BCDE为矩形,
∴DE=BC=,BE=CD,
又AB=AD=2CD,∴EA=AD,∴∠ADE=30°,
∴AE=DE,∴AE=1,∴AB=2,
∵PA=2,
在Rt△PAB中,tan∠PBA===,
∴∠PBA=60°,
∴二面角A﹣BC﹣P的大小为60°.
【点评】本题考查面面垂直的证明,考查二面角的大小的求法,属中档题.
19.(12分)黄山原名“黟山”,因峰岩青黑,遥望苍黛而名,后因传说轩辕黄帝曾在此炼丹,故改名为“黄山”.黄山雄踞风景秀丽的安徽南部,是我国最著名的山岳风景区之一.明代旅行家、地理学家徐霞客两游黄山,赞叹说:“登黄山天下无山,观止矣!”又留“五岳归来不看山,黄山归来不看岳”的美誉.为更好地提升旅游品质,黄山风景区的工作人员随机选择100名游客对景区进行满意度评分(满分100分),根据评分,制成如图所示的频率分布直方图.
(1)根据频率分布直方图,求x的值;
(2)估计这100名游客对景区满意度评分的40%分位数(得数保留两位小数);
(3)景区的工作人员采用按比例分层抽样的方法从评分在[50,60),[60,70)的两组中共抽取6人,再从这6人中随机抽取2人进行个别交流,求选取的2人评分分别在[50,60)和[60,70)内各1人的概率.
【分析】(1)根据直方科中频率和为1,能求出结果.
(2)由百分位数的定义,结合频率分布直方图能求出结果.
(3)分别求出各组人数,利用列举法结合古典概型求解.
【解答】解:(1)由频率分布直方图得:
10(0.005+0.01+0.015+x+0.04)=1,
解得x=0.03.
(2)由10(0.005+0.01+0.015)=0.3<0.4<10(0.005+0.01+0.015+0.03)=0.6,
∴40%分位数在区间[80,90)内,令其为m,
则0.3+0.03×(m﹣80)=0.4,
解得m=80+≈83.33,
∴这100名游客对景区满意度评分的40%分位数为83.33分.
(3)∵评分在[50,60),[60,70)的频率分别为0.05,0.1,
则在[50,60)中抽取=2人,设为a,b,
在[60,70)中抽取人,设为C,D,E,F,
从这6人中随机抽取2人,基本事件有:
{a,b},{a,C},{a,D},{a,E},{a,F},{b,C},{b,D},{b,E},{b,F},{C,D},{C,E},C,F},{D,E},{D,F},{E,F},共15个,
设事件A表示”选取的2人评分分别在[50,60)和[60,70)内各1人“,
则事件A包含的基本事件有:
{a,C},{a,D},{a,E},{a,F},{b,C},{b,D},{b,E},{b,F},共8个,
∴选取的2人评分分别在[50,60)和[60,70)内各1人的概率为P==.
【点评】本题考查频率分布直方图、中位数、列举法、古典概型等基础知识,考查运算求解能力,是基础题.
20.(12分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,)的图象如图所示.将函数y=f(x)的图象向右平移个单位长度得到曲线C,把C上各点的横坐标伸长到原来的2倍,纵坐标不变,得到的曲线对应的函数记作y=g(x).
(1)求函数f(x)的单调减区间;
(2)求函数的最小值;
(3)若函数在(0,4π)内恰有6个零点,求m的值.
【分析】(1)根据所给图象求出函数f(x)的解析式,再列出关于x的不等式即可得解;
(2)由(1)结合给定图象变换求出g(x)的解析式,再求出h(x)并作变形即可得解;
(3)求出F(x)并令t=sinx,将F(x)=0转化为关于t的一元二次方程,按根所在区间讨论得解.
【解答】解:(1)观察图象得A=1,f(x)最小正周期为T,
则,则,
而,则+φ=+2kπ,k∈Z,
解得,k∈Z,
又,于是得,
所以,
函数的单调递减区间满足:,k∈Z,
得,k∈Z,
所以单调递减区间为,k∈Z;
(2)将函数y=f(x)的图象向右平移个单位长度得到曲线C,即y=sin[2(x﹣)+]=sin2x,
再把C上各点的横坐标伸长到原来的2倍,纵坐标不变,得到的曲线对应的函数记作y=g(x),
即g(x)=sinx,
所以h(x)=f()g(x)=sin(x+)sinx=(sinx+cosx)sinx
=sin2x+sinxcosx=+sin2x
=(sin2x﹣cos2x)+
=sin(2x﹣)+,
当时,函数确定最小值,即时,h(x)min=×(﹣1)+=﹣,
所以的最小值为﹣;
(3)依题意,m∈R,
令F(x)=0,可得2sin2x﹣msinx﹣1=0,
令t=sinx∈[﹣1,1],得2t2﹣mt﹣1=0,
由于Δ=m2+8>0,即方程必有两个不同的实数根t1,t2,
且,,
由知t1、t2异号,不妨设t1>0,t2<0,
①若t1>1,则,sinx=t1,无解,
而sinx=t2在(0,4π)内有四个零点,不符题意;
②若t1=1,则,sinx=1在(0,4π)内有2个零点,
而在(0,4π)内有4个零点,
即F(x)在(0,4π)内有6个零点,符合题意,
此时,得m=1;
③若0<t1<1,,sinx=t1在(0,4π)有4个零点,
则sinx=t2在(0,4π)内应恰有2个零点,必有t2=﹣1,
此时,,解得m=﹣1,
综上所述有m=1或m=﹣1.
【点评】本题考查三角函数的图象与性质以及函数零点的综合应用,属中档题.
21.(12分)如图,平面四边形ABCD中,AB=8,CD=3,,∠ADC=90°,∠BAD=30°,点E,F满足,,将△AEF沿EF翻折至△PEF,使得.
(1)证明:EF⊥PD;
(2)求五棱锥P﹣BCDEF的体积.
【分析】(1)先用勾股定理证明AE⊥EF,再证明EF⊥面PED即可;
(2)先证明PE为锥体的高,再用锥体的体积公式即可求解.
【解答】解:(1)证明:由AB=8,,,则AE=2,,则AF=4,
在△AEF中,∠BAD=30°,由余弦定理得,
所以AE2+EF2=AF2,则AE⊥EF,即EF⊥AD,
所以EF⊥PE,EF⊥DE,又PE∩DE=E,所以EF⊥平面PDE,
又PD 平面PDE,故EF⊥PD;
(2)因为CD⊥AD,EF⊥AD,所以CD∥EF,即CD⊥平面PED,
所以CD⊥PD,,
又,,所以PE2+ED2=PD2,所以PE⊥ED,由此得PE⊥底面BCDEF,PE即为五棱锥的高,
过B点作BG∥EF.则BG=2EF=4,
S底=S梯形EFBG+S梯形CDGB=×(2+4)×2+×(3+4)×=,
V=×S底×PE=××2=19.
【点评】本题考查线面垂直的判定定理以及性质定理,锥体的体积公式,属于中档题.
22.(12分)某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25米,为了便于游客休闲散步,该农庄决定在鱼塘内建三条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°.
(1)设∠BOE=α,试将△OEF的周长l表示成α的函数关系式,并求出此函数的定义域;
(2)经核算,三条走廊每米建设费用均为4000元,试问如何设计才能使建设总费用最低并求出最低总费用.
【分析】(1)要将△OEF的周长l表示成α的函数关系式,需把△OEF的三边分别用含有α的关系式来表示,而OE,
OF,分别可以在Rt△OBE,Rt△OAF中求解,利用勾股定理可求EF,从而可求.
(2)要求铺路总费用最低,只要求△OEF的周长l的最小值即可.由(1)得l=,α∈[,],
利用换元,设sinα+cosα=t,则sinαcosα=,从而转化为求函数在闭区间上的最小值.
【解答】解:(1)∵在Rt△BOE中,OB=25,∠B=90°,∠BOE=α,
∴OE=
在Rt△AOF中,OA=25,∠A=90°,∠AFO=α,
∴OF=.
又∠EOF=90°,
∴EF==,
∴l=OE+OF+EF=.
当点F在点D时,这时角α最小,此时α=;
当点E在C点时,这时角α最大,求得此时α=.
故此函数的定义域为[,];
(2)由题意知,要求铺路总费用最低,只要求△OEF的周长l的最小值即可.
由(1)得,l=,α∈[,],
设sinα+cosα=t,则sinαcosα=,
∴l==
由t=sinα+cosα=sin(α+),
又≤α+≤,得,
∴,
从而当α=,即BE=25时,lmin=50(+1),
所以当BE=AF=25米时,铺路总费用最低,最低总费用为200000(+1)元.
【点评】本题主要考查了借助于三角函数解三角形在实际问题中的应用,考查了利用数学知识解决实际问题的能力,及推理运算的能力.
同课章节目录
