成比例线段与比例的基本性质
文档属性
| 名称 | 成比例线段与比例的基本性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 481.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-08 00:00:00 | ||
图片预览






文档简介
课件27张PPT。成比例线段与比例的基本性质、两条线段的比:
问题:在Rt△ABC中,∠C=90°,AC=4,BC=3,
则AB= 。
那么:
定义:如果选用同一长度单位量得两条线段a,b的
长度分别为m,n. 那么就说这两条线段的比是a:b=m:n,
或写成
(其中a叫作比的前项,b叫作比的后项)
例1:正方形的对角线m与边长a的比是: 。练习1:填空,在等边三角形ABC中,AD⊥BC与D,求下列
各比的值:
AB:AC= AB:BD= BD:AD=
或:
注意:AB:BD=2:1,其中的1不能省略;但分式中分母
1可以省略;AB是BD的2倍。
,其中但在分式中要化简成可以,BD:AD=1:线段的比要注意:
1:数的比可以是正数也可以是负数,
但线段的比都是正数;
2:两条线段的比与所采用的长度单位无关,讨论线段的比时一般不指明单位,但度量两条线段的单位要一致。
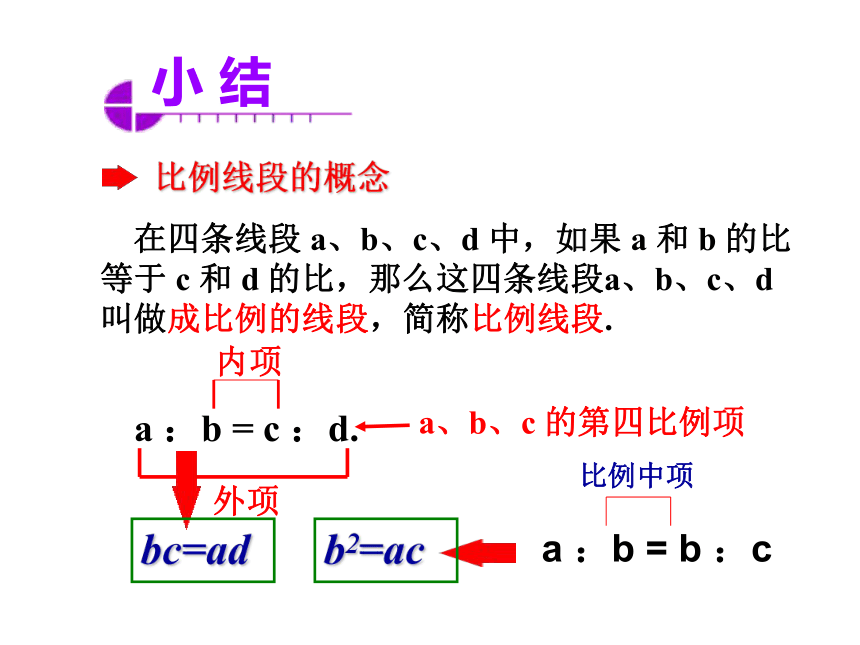
对于四条线段a、b、c、d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即那么这四条线段叫做成比例线段,简称
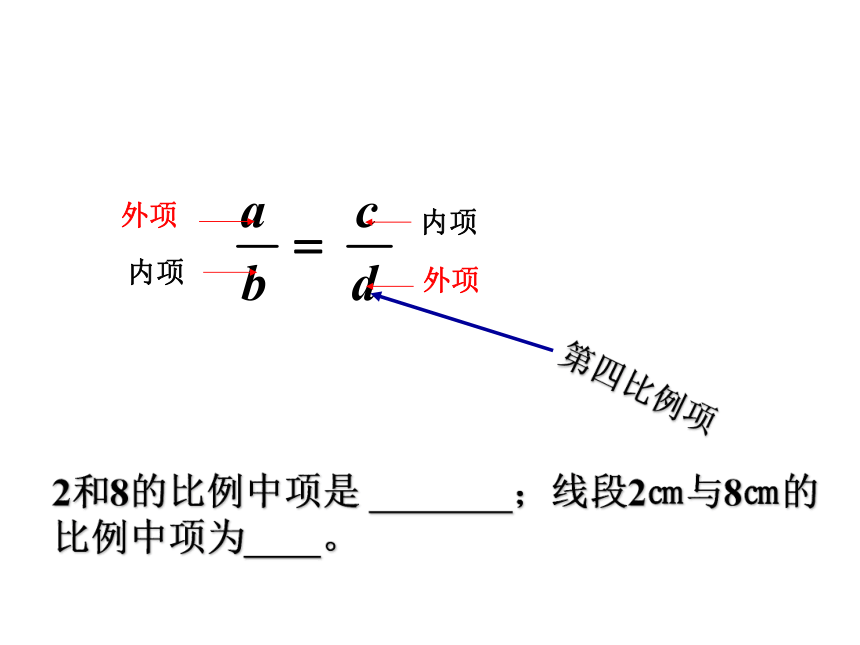
比例线段。 二:比例线段 其中a,b,c,d叫作组成比例的项,线段a,d叫作比例的外项,b,c叫作比例的内项。线段d叫作a,b,c的第四比例项(注意a,b,c,d是有序的)
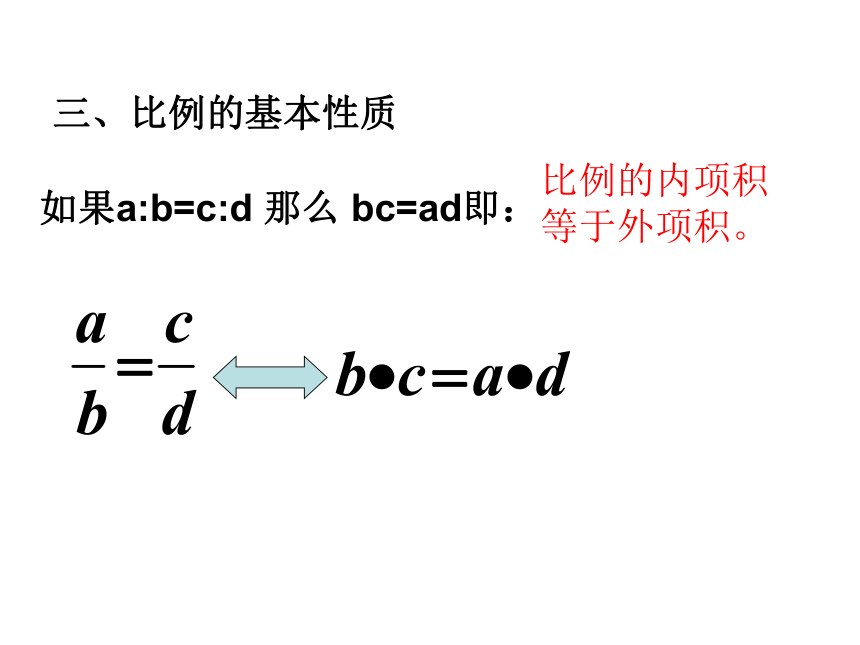
如果a:b=b:c,那么线段b叫作比例中项。2和8的比例中项是 ???????????????;线段2㎝与8㎝的比例中项为 。 比例线段的概念a :b = c :d.a、b、c 的第四比例项a :b = b :c 在四条线段 a、b、c、d 中,如果 a 和 b 的比等于 c 和 d 的比,那么这四条线段a、b、c、d 叫做成比例的线段,简称比例线段.小 结b2=acbc=ad三、比例的基本性质如果a:b=c:d 那么 bc=ad即:比例的内项积
等于外项积。例1:线段a=15厘米,b=20cm,c=7.5cm,
d=0.1m,求: ,这四条线段会成比例吗? 解 c=75毫米=7.5厘米,d=0.1米=10厘米它们会成比例. 在线段求比时,两条线段的单位要统一.例2:如图AB=21,AD=15,CE=4,并且求:AC的长 解 设AC=x,则AE=AC-CE=x-4因为AD:AB=AE:AC,
因此得15:21=(x-4):x根据比例性质得:21(x-4)=15x 解这个方程得x=14. 1.下列四条线段中,不能成比例的是( ) A. a=3,b=6,c=2,d=4B. a=1,b=,c=,d=C. a=4,b=6,c=5,d=10D. a=2,b=,c=,d=2C2.若,则的值为( ) A. B. C.3 5 D.2B1.若b是5,15的比例中项,则b= .
2.若a=3cm,a, b的比例中项是9cm,
则b= cm. 1.已知三条线的比如下,可以组成三角形的是( ) A.5:20:30 B.10:20:30C.15:15:30 D.20:30:30 2.若a, x, b, y是成比例线段,
则比例式 为 ;
若a=1,x=-2, b=-2.5, 则y= . 3.若d是5,-8,-3的第四比例项,
则d= ;
4.若b是5,15的比例中项,则b= .
5.若a=3cm,a, b的比例中项是9cm,
则b= cm.(1)比例的基本性质如果 a:b =c:d ,那么ad =bc.比例的内项乘积等于外项乘积.如果 ad =bc,那么 a:b =c:d .(2)合比性质说明:例1、已知 = ,求 .x+y 5 x
3y 4 y解:1.若x∶(x+1)=7∶9,则x= ; 2.若 = ,则 = . 3.若5a=3b,则 = , = . 例2、已知 a:b:c=2:5:6,
求 的值.2a+5b–c
3a–2b+c解:设 a=2k,b=5k,c=6k,若a:b:c=2:3:7,又a+b+c=36,求a、b 、c的值。如图,已知 那么 DF
EF理由:ABCDEF如图,已知 那么 DF
DE理由:ABCDEF如图,已知 那么 EF
DE理由:ABCDEF如图,已知 那么 AF
AC理由:ABCEF如图,已知 那么 AF
AC理由:ABCEF
问题:在Rt△ABC中,∠C=90°,AC=4,BC=3,
则AB= 。
那么:
定义:如果选用同一长度单位量得两条线段a,b的
长度分别为m,n. 那么就说这两条线段的比是a:b=m:n,
或写成
(其中a叫作比的前项,b叫作比的后项)
例1:正方形的对角线m与边长a的比是: 。练习1:填空,在等边三角形ABC中,AD⊥BC与D,求下列
各比的值:
AB:AC= AB:BD= BD:AD=
或:
注意:AB:BD=2:1,其中的1不能省略;但分式中分母
1可以省略;AB是BD的2倍。
,其中但在分式中要化简成可以,BD:AD=1:线段的比要注意:
1:数的比可以是正数也可以是负数,
但线段的比都是正数;
2:两条线段的比与所采用的长度单位无关,讨论线段的比时一般不指明单位,但度量两条线段的单位要一致。
对于四条线段a、b、c、d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即那么这四条线段叫做成比例线段,简称
比例线段。 二:比例线段 其中a,b,c,d叫作组成比例的项,线段a,d叫作比例的外项,b,c叫作比例的内项。线段d叫作a,b,c的第四比例项(注意a,b,c,d是有序的)
如果a:b=b:c,那么线段b叫作比例中项。2和8的比例中项是 ???????????????;线段2㎝与8㎝的比例中项为 。 比例线段的概念a :b = c :d.a、b、c 的第四比例项a :b = b :c 在四条线段 a、b、c、d 中,如果 a 和 b 的比等于 c 和 d 的比,那么这四条线段a、b、c、d 叫做成比例的线段,简称比例线段.小 结b2=acbc=ad三、比例的基本性质如果a:b=c:d 那么 bc=ad即:比例的内项积
等于外项积。例1:线段a=15厘米,b=20cm,c=7.5cm,
d=0.1m,求: ,这四条线段会成比例吗? 解 c=75毫米=7.5厘米,d=0.1米=10厘米它们会成比例. 在线段求比时,两条线段的单位要统一.例2:如图AB=21,AD=15,CE=4,并且求:AC的长 解 设AC=x,则AE=AC-CE=x-4因为AD:AB=AE:AC,
因此得15:21=(x-4):x根据比例性质得:21(x-4)=15x 解这个方程得x=14. 1.下列四条线段中,不能成比例的是( ) A. a=3,b=6,c=2,d=4B. a=1,b=,c=,d=C. a=4,b=6,c=5,d=10D. a=2,b=,c=,d=2C2.若,则的值为( ) A. B. C.3 5 D.2B1.若b是5,15的比例中项,则b= .
2.若a=3cm,a, b的比例中项是9cm,
则b= cm. 1.已知三条线的比如下,可以组成三角形的是( ) A.5:20:30 B.10:20:30C.15:15:30 D.20:30:30 2.若a, x, b, y是成比例线段,
则比例式 为 ;
若a=1,x=-2, b=-2.5, 则y= . 3.若d是5,-8,-3的第四比例项,
则d= ;
4.若b是5,15的比例中项,则b= .
5.若a=3cm,a, b的比例中项是9cm,
则b= cm.(1)比例的基本性质如果 a:b =c:d ,那么ad =bc.比例的内项乘积等于外项乘积.如果 ad =bc,那么 a:b =c:d .(2)合比性质说明:例1、已知 = ,求 .x+y 5 x
3y 4 y解:1.若x∶(x+1)=7∶9,则x= ; 2.若 = ,则 = . 3.若5a=3b,则 = , = . 例2、已知 a:b:c=2:5:6,
求 的值.2a+5b–c
3a–2b+c解:设 a=2k,b=5k,c=6k,若a:b:c=2:3:7,又a+b+c=36,求a、b 、c的值。如图,已知 那么 DF
EF理由:ABCDEF如图,已知 那么 DF
DE理由:ABCDEF如图,已知 那么 EF
DE理由:ABCDEF如图,已知 那么 AF
AC理由:ABCEF如图,已知 那么 AF
AC理由:ABCEF
