24.1.4圆周角
图片预览











文档简介
课件32张PPT。24.1.4圆周角(一)教材分析
本课是在学习了圆心角后进而要学习的圆的又一个重要的性质,它在推理、论证和计算中应用比较广泛,是本章重点内容之一。是今后学习圆的有关性质和利用相似证明成比例线段的基础。另外它也是和三角函数、勾股定理、三角形、四边形等几何知识综合的结合点。教学目标知识与技能:
理解并掌握圆周角的概念;掌握圆周角定理,并能熟练地运用它们进行论证和计算.
过程与方法:
经历探究同弧上的圆周角与圆心角之间关系的过程,体会由特殊到一般思考数学问题的方法,通过反思获得解决问题经验, 通过圆周角定理的证明,进一步领悟分类讨论和转化的数学思想。
情感与态度: 通过猜测、验证、类比、归纳、推理论证,体验数学活动充满探索性和创造性, 激发学生能积极参与数学学习活动,对数学有好奇心与求知欲,并能在学习活动中获得成功。
教学重点:圆周角定理。 教学难点: 认识圆周角定理需要分三种情况逐一证明的必要性。
(二)本节教材安排 本节共分两个课时,第一课时主要研究圆周角和圆心角的关系及推论,第二课时研究圆周角定理的应用,并解决一些简单问题。今天我向大家汇报的是第一课时的设计。
(三)教学方法 数学教学是师生之间、学生之间交往互动与共同发展的过程,因此,我认为教法与学法是密不可分的。本节主要采取探究合作、启发引导的教学方法,多媒体的运用,激发了学生探究合作的积极性,为教师的启发引导提供了生动的素材,使学生获得知识,形成技能。(四)教学过程
活动1 旧知回放,探索新知
设计意图:让学生学好基础知识、基本概念,感受其内容反映出来的数学思想和方法,培养学生的基本技能、分析问题和解决问题的能力,使学生理解并掌握圆周角的定义。
?
活动2 探索同弧所对的圆心角与圆周角关系;同弧所对的圆周角之间的关系.设计意图:通过实例观察、发现圆周角的特点,利用度量工具,猜想
同弧所对的圆心角与圆周角关系;同弧所对的圆周角之间的关系.活动3 发现并证明圆周角定理,探索圆心与圆周角的位置关系,利用分类讨论的数学思想证明圆周角定理.
合作探索,突破难点
活动4 圆周角定理应用
反馈练习,加深对圆周角定理的理解和应用.
活动5 小结,布置作业?
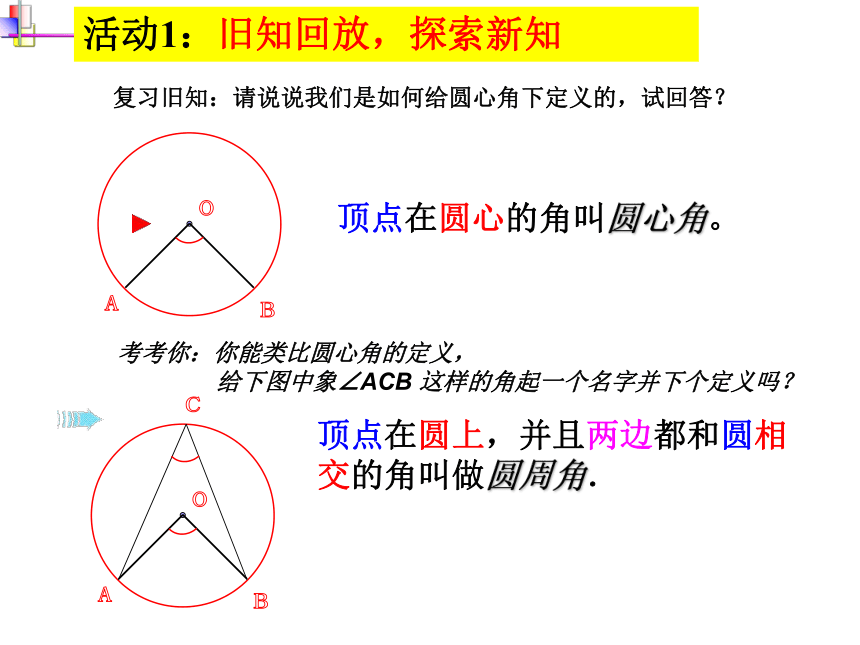
回顾梳理,从知识和能力方面总结本节课所学到的东西 复习旧知:请说说我们是如何给圆心角下定义的,试回答?顶点在圆心的角叫圆心角。考考你:你能类比圆心角的定义,
给下图中象∠ACB 这样的角起一个名字并下个定义吗?顶点在圆上,并且两边都和圆相交的角叫做圆周角. 活动1:旧知回放,探索新知你能总结出圆周角的特征吗?你能说出圆周角与圆心角的区别吗?① 角的顶点在圆上.② 角的两边都与圆相交.练习:判断下列各图中,哪些是圆周角,为什么? oABoABoABoABoABoABoABoABCCCCCCCC图1图2图3图4图5图6图7图8图9深入理解概念:思考并讨论1.同弧所对的圆周角有多少个?
2.圆心和圆周角有几种相对位置关系?你能画出来吗?
3. 同弧所对圆周角和所含圆周角有区别吗?ABCOABCCOOAB一个圆的圆心与圆周角有三种关系...在这三个图中,哪个图形最特殊?其余两个可以转化成这个图形吗?DD如图是一个圆柱形的海洋馆的横截面的示意图,人们可以通过其中的圆弧形玻璃AB 观看窗内的海洋动物,同学甲站在圆心的O 位置,同学乙站在正对着玻璃窗的靠墙的位置C,他们的视角(∠AOB 和∠ACB)有什么关系?如果同学丙、丁分别站在他靠墙的位置D和E,他们的视角( ∠ADB 和∠AEB )和同学乙的视角相同吗?活动2:创设情境,大胆猜想它们之间有什么关系呢?·CDABO猜想:同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.分别量一下图中AB弧所对的两个圆周角的度数,比较一下,再变动点C在圆周上的位置,圆周角的度数有没有变化?你能发现什么规律吗?
再分别量出图中AB弧所对的圆周角和圆心角的度数,比较一下,你什么发现?大胆猜想活动三:合作交流,证明猜想 命题:
在同圆或等圆中,同弧所对的圆周角等于它所对的圆心角的一半。分三种情况来证明:
(1)圆心在∠BAC的一边上.
AOBC(2)圆心在圆周角的内部.圆心O在∠BAC的内部,作直径AD,利用(1)的结果,有·COABD(3)圆心在圆周角的外部.圆心O在∠BAC的外部,作直径AD,利用(1)的结果,有·COABD概括定理,回顾证明,体会分类讨论的必要性思考:将定理中的同弧或等弧改为同弦或等弦结论是否成立?·ABC1OC2C3·ABCO例1 如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?ABCD12345678∠1 = ∠4∠5 = ∠8∠2 = ∠7∠6 = ∠3活动4:例题讲解 巩固练习典型例题 例2 在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A练习: 已知:如图,四边形ABCD的四个顶点在⊙O上,求证:∠B+∠D=1800OCBAD练习:已知∠OAB等于40度,求∠C的度数. 小结与收获1、本节课我们学习了哪些知识?
2、 掌握了哪些数学方法?
3、体会到了哪些数学思想?
理解并掌握圆周角的概念;掌握圆周角定理,并能熟练地运用它们进行论证和计算.
过程与方法:
经历探究同弧上的圆周角与圆心角之间关系的过程,体会由特殊到一般思考数学问题的方法,通过反思获得解决问题经验, 通过圆周角定理的证明,进一步领悟分类讨论和转化的数学思想。
情感与态度: 通过猜测、验证、类比、归纳、推理论证,体验数学活动充满探索性和创造性, 激发学生能积极参与数学学习活动,对数学有好奇心与求知欲,并能在学习活动中获得成功。
教学重点:圆周角定理。 教学难点: 认识圆周角定理需要分三种情况逐一证明的必要性。
(二)本节教材安排 本节共分两个课时,第一课时主要研究圆周角和圆心角的关系及推论,第二课时研究圆周角定理的应用,并解决一些简单问题。今天我向大家汇报的是第一课时的设计。
(三)教学方法 数学教学是师生之间、学生之间交往互动与共同发展的过程,因此,我认为教法与学法是密不可分的。本节主要采取探究合作、启发引导的教学方法,多媒体的运用,激发了学生探究合作的积极性,为教师的启发引导提供了生动的素材,使学生获得知识,形成技能。(四)教学过程
活动1 旧知回放,探索新知
设计意图:让学生学好基础知识、基本概念,感受其内容反映出来的数学思想和方法,培养学生的基本技能、分析问题和解决问题的能力,使学生理解并掌握圆周角的定义。
?
活动2 探索同弧所对的圆心角与圆周角关系;同弧所对的圆周角之间的关系.设计意图:通过实例观察、发现圆周角的特点,利用度量工具,猜想
同弧所对的圆心角与圆周角关系;同弧所对的圆周角之间的关系.活动3 发现并证明圆周角定理,探索圆心与圆周角的位置关系,利用分类讨论的数学思想证明圆周角定理.
合作探索,突破难点
活动4 圆周角定理应用
反馈练习,加深对圆周角定理的理解和应用.
活动5 小结,布置作业?
回顾梳理,从知识和能力方面总结本节课所学到的东西 复习旧知:请说说我们是如何给圆心角下定义的,试回答?顶点在圆心的角叫圆心角。考考你:你能类比圆心角的定义,
给下图中象∠ACB 这样的角起一个名字并下个定义吗?顶点在圆上,并且两边都和圆相交的角叫做圆周角. 活动1:旧知回放,探索新知你能总结出圆周角的特征吗?你能说出圆周角与圆心角的区别吗?① 角的顶点在圆上.② 角的两边都与圆相交.练习:判断下列各图中,哪些是圆周角,为什么? oABoABoABoABoABoABoABoABCCCCCCCC图1图2图3图4图5图6图7图8图9深入理解概念:思考并讨论1.同弧所对的圆周角有多少个?
2.圆心和圆周角有几种相对位置关系?你能画出来吗?
3. 同弧所对圆周角和所含圆周角有区别吗?ABCOABCCOOAB一个圆的圆心与圆周角有三种关系...在这三个图中,哪个图形最特殊?其余两个可以转化成这个图形吗?DD如图是一个圆柱形的海洋馆的横截面的示意图,人们可以通过其中的圆弧形玻璃AB 观看窗内的海洋动物,同学甲站在圆心的O 位置,同学乙站在正对着玻璃窗的靠墙的位置C,他们的视角(∠AOB 和∠ACB)有什么关系?如果同学丙、丁分别站在他靠墙的位置D和E,他们的视角( ∠ADB 和∠AEB )和同学乙的视角相同吗?活动2:创设情境,大胆猜想它们之间有什么关系呢?·CDABO猜想:同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.分别量一下图中AB弧所对的两个圆周角的度数,比较一下,再变动点C在圆周上的位置,圆周角的度数有没有变化?你能发现什么规律吗?
再分别量出图中AB弧所对的圆周角和圆心角的度数,比较一下,你什么发现?大胆猜想活动三:合作交流,证明猜想 命题:
在同圆或等圆中,同弧所对的圆周角等于它所对的圆心角的一半。分三种情况来证明:
(1)圆心在∠BAC的一边上.
AOBC(2)圆心在圆周角的内部.圆心O在∠BAC的内部,作直径AD,利用(1)的结果,有·COABD(3)圆心在圆周角的外部.圆心O在∠BAC的外部,作直径AD,利用(1)的结果,有·COABD概括定理,回顾证明,体会分类讨论的必要性思考:将定理中的同弧或等弧改为同弦或等弦结论是否成立?·ABC1OC2C3·ABCO例1 如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?ABCD12345678∠1 = ∠4∠5 = ∠8∠2 = ∠7∠6 = ∠3活动4:例题讲解 巩固练习典型例题 例2 在⊙O中,∠CBD=30° ,∠BDC=20°,求∠A练习: 已知:如图,四边形ABCD的四个顶点在⊙O上,求证:∠B+∠D=1800OCBAD练习:已知∠OAB等于40度,求∠C的度数. 小结与收获1、本节课我们学习了哪些知识?
2、 掌握了哪些数学方法?
3、体会到了哪些数学思想?
同课章节目录
