新人教版八年级下第十四章第二节勾股定理(第1课时)
文档属性
| 名称 | 新人教版八年级下第十四章第二节勾股定理(第1课时) |

|
|
| 格式 | rar | ||
| 文件大小 | 675.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-08 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
勾股定理
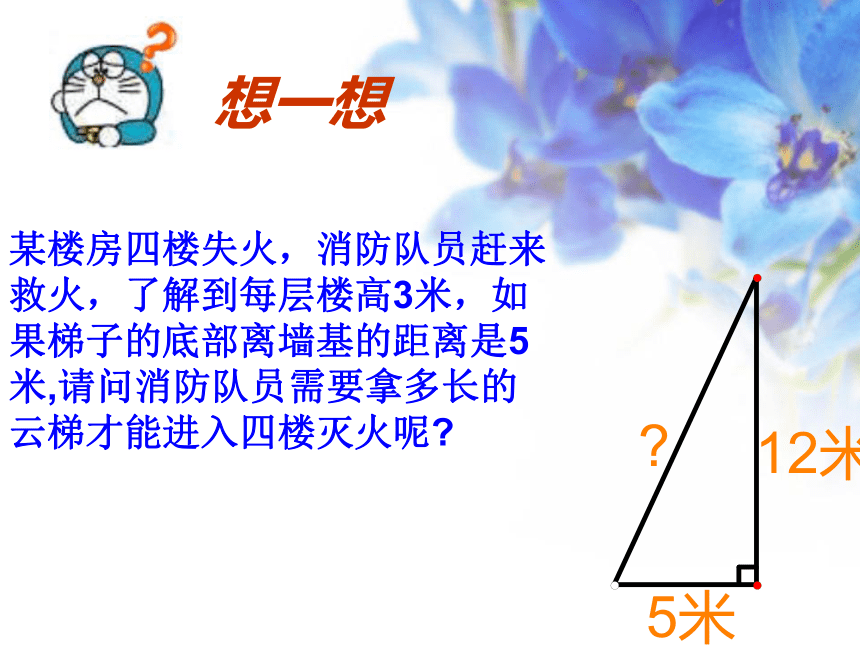
某楼房四楼失火,消防队员赶来救火,了解到每层楼高3米,如果梯子的底部离墙基的距离是5米,请问消防队员需要拿多长的云梯才能进入四楼灭火呢
想一想
A
B
C
A
B
C
图乙
图甲
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图甲
图乙
A、B、C面积关系
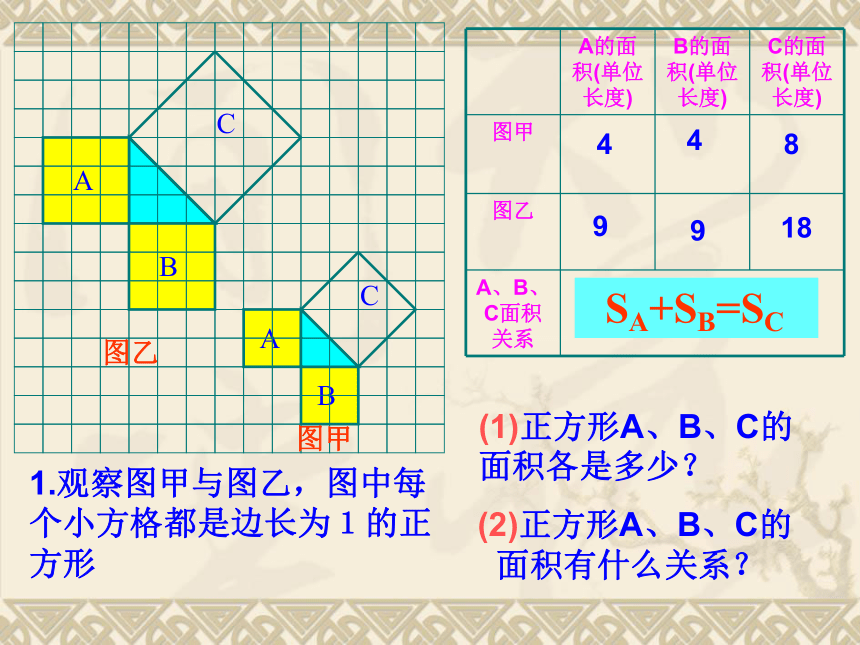
SA+SB=SC
1.观察图甲与图乙,图中每个小方格都是边长为1的正方形
(2)正方形A、B、C的
面积有什么关系?
(1)正方形A、B、C的面积各是多少?
4
8
4
9
18
9
4
4
8
A
B
C
SA+SB=SC
图甲
图甲
A的面积
B的面积
C的面积
a
b
c
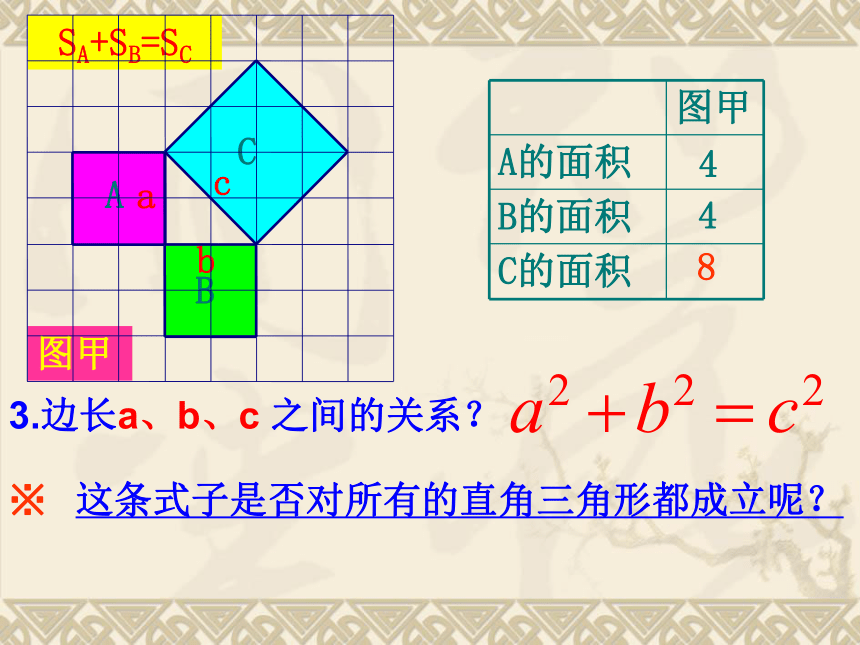
3.边长a、b、c 之间的关系?
※ 这条式子是否对所有的直角三角形都成立呢?
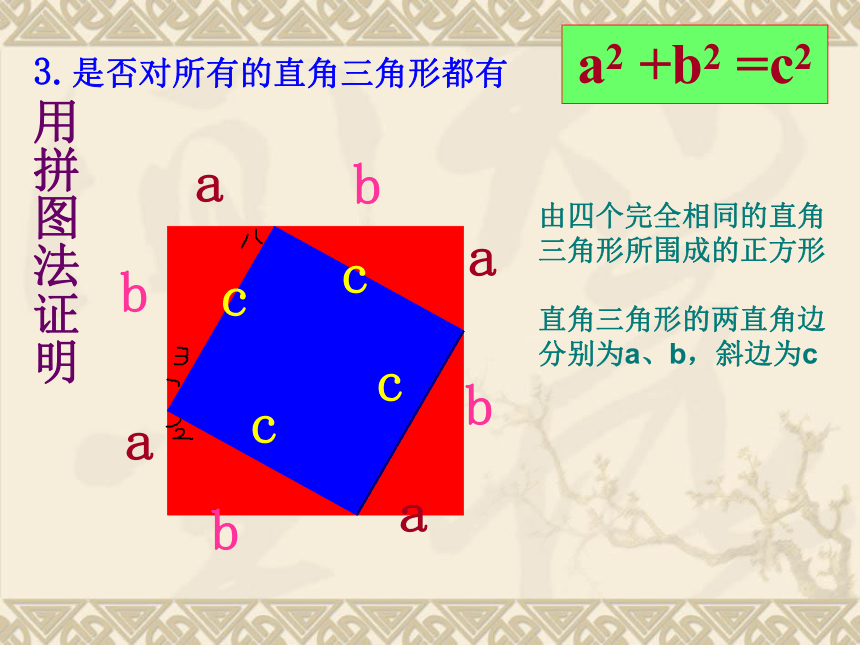
3.是否对所有的直角三角形都有
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.是否对所有的直角三角形都有
a2 +b2 =c2
由四个完全相同的直角
三角形所围成的正方形
直角三角形的两直角边
分别为a、b,斜边为c
勾股定理(毕达哥拉斯定理)
如果直角三角形两直角边分
别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于 斜边的平方.
a
c
b
写出下面三角形的勾股定理表达式:
没有(不是直角三角形)
想一想
∴消防员需要拿13米长的云梯.
某楼房四楼失火,消防队员赶来救火,了解到每层楼高3米,如果梯子的底部离墙基的距离是5米,请问消防队员需要拿多长的云梯才能进入四楼灭火呢
在国外,相传勾股定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。法国和比利时称它为“驴桥定理”,埃及称它为“埃及三角形”等。但他们发现的时间都比我国要迟得多。
中国最早的一部数学著作——《周髀算经》的开头,记载着一段周公向商高请教数学知识的对话:周公问:“我听说您对数学非常精通,我想请教一下:天没有梯子可以上去,地也没法用尺子去一段一段丈量,那么怎样才能得到关于天地得到数据呢?” 商高回答说:“数的产生来源于对方和圆这些形体的认识。其中有一条原理:当直角三角形‘矩‘得到的一条直角边‘勾’等于3,另一条直角边’股‘等于4的时候,那么它的斜边‘弦’就必定是5。这个原理是大禹在治水的时候就总结出来的呵。"
如果说大禹治水因年代久远而无法确切考证的话,那么周公与商高的对话则可以确定在公元1100年左右的西周时期,比毕达哥拉斯要早了五百年其中所说的勾3股4弦5,正是勾股定理的一个应用特例。所以现在数学界把它称为勾股定理是非常恰当的。
在《九章算术》一书中(右图),勾股定理得到了更加规范的一般性表达。书中的《勾股章》说;“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。
1.收集勾股定理的相关历史,下节课一起交流.
2.复习这节课的内容和预习勾股定理的运
用.并完成下面思考题:
在Rt△ABC中,∠A=90°.
(1) 已知:c=6,b=8,求a;
(2) 已知:a=13,b=5,求c;
(3) 已知: c:b=3:4, a=15,求b、c.
谢谢大家的配合!
勾股定理
某楼房四楼失火,消防队员赶来救火,了解到每层楼高3米,如果梯子的底部离墙基的距离是5米,请问消防队员需要拿多长的云梯才能进入四楼灭火呢
想一想
A
B
C
A
B
C
图乙
图甲
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图甲
图乙
A、B、C面积关系
SA+SB=SC
1.观察图甲与图乙,图中每个小方格都是边长为1的正方形
(2)正方形A、B、C的
面积有什么关系?
(1)正方形A、B、C的面积各是多少?
4
8
4
9
18
9
4
4
8
A
B
C
SA+SB=SC
图甲
图甲
A的面积
B的面积
C的面积
a
b
c
3.边长a、b、c 之间的关系?
※ 这条式子是否对所有的直角三角形都成立呢?
3.是否对所有的直角三角形都有
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.是否对所有的直角三角形都有
a2 +b2 =c2
由四个完全相同的直角
三角形所围成的正方形
直角三角形的两直角边
分别为a、b,斜边为c
勾股定理(毕达哥拉斯定理)
如果直角三角形两直角边分
别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于 斜边的平方.
a
c
b
写出下面三角形的勾股定理表达式:
没有(不是直角三角形)
想一想
∴消防员需要拿13米长的云梯.
某楼房四楼失火,消防队员赶来救火,了解到每层楼高3米,如果梯子的底部离墙基的距离是5米,请问消防队员需要拿多长的云梯才能进入四楼灭火呢
在国外,相传勾股定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。法国和比利时称它为“驴桥定理”,埃及称它为“埃及三角形”等。但他们发现的时间都比我国要迟得多。
中国最早的一部数学著作——《周髀算经》的开头,记载着一段周公向商高请教数学知识的对话:周公问:“我听说您对数学非常精通,我想请教一下:天没有梯子可以上去,地也没法用尺子去一段一段丈量,那么怎样才能得到关于天地得到数据呢?” 商高回答说:“数的产生来源于对方和圆这些形体的认识。其中有一条原理:当直角三角形‘矩‘得到的一条直角边‘勾’等于3,另一条直角边’股‘等于4的时候,那么它的斜边‘弦’就必定是5。这个原理是大禹在治水的时候就总结出来的呵。"
如果说大禹治水因年代久远而无法确切考证的话,那么周公与商高的对话则可以确定在公元1100年左右的西周时期,比毕达哥拉斯要早了五百年其中所说的勾3股4弦5,正是勾股定理的一个应用特例。所以现在数学界把它称为勾股定理是非常恰当的。
在《九章算术》一书中(右图),勾股定理得到了更加规范的一般性表达。书中的《勾股章》说;“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。
1.收集勾股定理的相关历史,下节课一起交流.
2.复习这节课的内容和预习勾股定理的运
用.并完成下面思考题:
在Rt△ABC中,∠A=90°.
(1) 已知:c=6,b=8,求a;
(2) 已知:a=13,b=5,求c;
(3) 已知: c:b=3:4, a=15,求b、c.
谢谢大家的配合!
