简易方程 第1课时 用字母表示数 课件(共20张PPT)-人教版数学五年级上册
文档属性
| 名称 | 简易方程 第1课时 用字母表示数 课件(共20张PPT)-人教版数学五年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1007.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-25 20:41:09 | ||
图片预览








文档简介
(共20张PPT)
用字母表示数
第五单元 简易方程
b+a
a+b
运算定律 定律内容
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
我们已经学过哪些运算定律?请你用语言叙述一下对应的运算定律的具体内容。
两个数相加,交换加数的位置,它们的和不变。
两三个数相加,先把前两个数相加,再同第三个数相加;或者先把 后两个数相加,再同第一个数相加,它们的和不变。
两个数相乘,交换因数的位置,它们的积不变。
三个数相乘,先把前两个数相乘,再同第三个数相乘;或者先把后两个 数相乘,再同第一个数相乘,它们的积不变。
两个数的和同一个数相乘,可以把两个加数分别同这个数相乘 ,再把两个积相加,结果不变 。
课题引入
定律名称 字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
课题引入
你能像上节课那样,用字母把这些运算定律表示出来吗?
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
课题引入
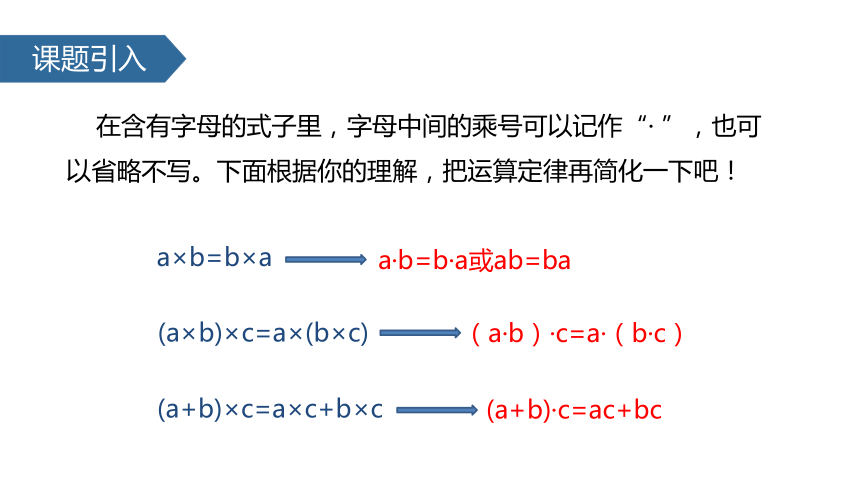
在含有字母的式子里,字母中间的乘号可以记作“· ”,也可以省略不写。下面根据你的理解,把运算定律再简化一下吧!
a×b=b×a
a·b=b·a或ab=ba
(a×b)×c=a×(b×c)
(a·b)·c=a·(b·c)
(a+b)×c=a×c+b×c
(a+b)·c=ac+bc
知识梳理
知识点1:用字母表示运算定律或公式。
由于用文字叙述运算定律或公式比较麻烦,有时还说不清,所以可以用字母来表示运算定律或公式。
知识梳理
例题:用字母表示乘法结合律( )。
【解析】乘法结合律指的是:三个数相乘,可以先把前两个数相乘,再同第三个数相乘,也可以先把后两个数相乘,再同第一个数相乘,它们的积不变。准确把握乘法结合律的内容后,可以选择喜欢的字母表示,如(a b)c=a(b c)。
【方法小结】在用字母表示运算定律时,通常用字母a、b、c表示。
(a b)c=a(b c)
知识梳理
知识点2:在用字母表示数中省略乘号。
在用字母表示数时,字母与数字相乘可以乘略乘号或写成 ·,并要把数字放到字母前面;当两个相同的数字或字母相乘时要写成平方的形成,如a a就要写成a ,读作a的平方。
知识梳理
例题:长方形的长是15米,宽是3米,求这个长方形的周长和面积。(a表示长,b表示宽,先写出字母公式,再计算)
【解析】根据长方形的周长=(长+宽)×2 ,面积=长×宽,可以根据字母写出长方形的周长和面积,分别为c=2(a+b)和s=ab,然后再进行计算。
答案:c=2(a+b)=2×(15+3)=36(米)s=ab=15×3=45(平方米)。
【方法小结】在运用字母公式进行计算时,代入的数字要与字母表示的意义一一对应。
知识梳理
【小练习】判断题。
(1)q×1=q ( )
(2)4+a=4a ( )
(3)10×2=10 ( )
(4)8×2=82 ( )
√
×
×
×
课堂作业
1 . 公正的小判官。
(1)a 和2a意义一样。 ( )
(2)a+3可以写成3a。 ( )
(3)a×4可以写成4a。 ( )
(4)5×8的乘号可以省略不写。 ( )
(5)b×2×c写作2bc ( )
×
×
√
×
√
课堂作业
2 . 想一想,填一填。
(1)b与21的和是( ),积是( )
(2)比c少3.2的数是( )
(3)每盒装5块月饼,c盒装( )块月饼。
(4)5本故事书x元,平均每本故事书( )元
(5)淘气今年f岁,爸爸比他大28岁,爸爸今年( )岁。
b+21
21b
c-3.2
5c
x÷5
28+f
课堂练习
3 . 冬冬去超市购物。
食品 牛奶 面包 巧克力
单价 a 元 3元 b 元
(1)一瓶牛奶和一块巧克力( )元。
(2)一块巧克力比一只面包多( )元。
(3)买10瓶牛奶( )元。
(4)80元可以买巧克力( )块。
a+b
b-3
10a
80÷b
课堂练习
4 . 一块平行四边形的菜地,底是6米,高是8米,这块菜地的面积是多少?
答案:S = ah = 6×8 = 4 8(平方米)
(1)a+2.6= + ;b×15= ×
(2)n×8×1.25= ×( × )
(3)(12+16)×c= × + ×
(4)168-35-65= -( + )
课后作业
1 . 根据运算定律填空。
2.6
a
15
b
n
8
1.25
12
c
16
c
168
35
65
课后作业
2 . 用含有字母的式子表示下面各题的数量关系。
(1)在一个三角形中,∠1=a°,∠2=b°,用含有字母的式子表示∠3的度数。
(2)在一个等腰三角形中,底角是a°,用含有字母的式子表示顶角的度数。
答案:180°-a°-b°
答案:180°-2a°
课后作业
2 . 用含有字母的式子表示下面各题的数量关系。
(3)一个正方形的周长是C,用含有字母的式子表示这个正方形的边长。
答案:C÷4
(4)比x的5倍多20的数。
答案:5x+20
(5)比x多20的数是5的多少倍?
答案:(x+20)÷5
3 . 根据公式进行计算。
课后作业
(1)一个长方形长是15分米宽是8分米,求面积?
答案:15×8=120(平方分米)
(2)一个正方形边长是12厘米,求面积?
答案:12×12=144(平方厘米)
(3)一个长方形长是15厘米,宽是6厘米,求周长?
答案:(15+6)×2=42(厘米)
4 . 青青林场栽了梧桐树和雪松各x排,已知梧桐树每排12棵,雪松每排14棵。
课后作业
(1)栽梧桐树和雪松共多少棵?
答案:(12+14)x
(2)当x=20时,青青林场一共有多少棵梧桐树和雪松?
答案:(12+14)×20=520棵
课后作业
5 . 一辆汽车,每小时行驶a千米,上午行驶4小时,下午行驶了b小时。一天共行多少千米?
答案:(4+b)a
知识拓展
用简便方法计算下面各题,再用字母表示出简算思路。
278-23.5-6.5 780÷125÷8
=278-(23.5+6.5)
=248 a-b-c=a-(b+c)
=780 ÷(125×8)
=0.78
a÷b÷c=a÷(bc)
用字母表示数
第五单元 简易方程
b+a
a+b
运算定律 定律内容
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
我们已经学过哪些运算定律?请你用语言叙述一下对应的运算定律的具体内容。
两个数相加,交换加数的位置,它们的和不变。
两三个数相加,先把前两个数相加,再同第三个数相加;或者先把 后两个数相加,再同第一个数相加,它们的和不变。
两个数相乘,交换因数的位置,它们的积不变。
三个数相乘,先把前两个数相乘,再同第三个数相乘;或者先把后两个 数相乘,再同第一个数相乘,它们的积不变。
两个数的和同一个数相乘,可以把两个加数分别同这个数相乘 ,再把两个积相加,结果不变 。
课题引入
定律名称 字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
课题引入
你能像上节课那样,用字母把这些运算定律表示出来吗?
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
课题引入
在含有字母的式子里,字母中间的乘号可以记作“· ”,也可以省略不写。下面根据你的理解,把运算定律再简化一下吧!
a×b=b×a
a·b=b·a或ab=ba
(a×b)×c=a×(b×c)
(a·b)·c=a·(b·c)
(a+b)×c=a×c+b×c
(a+b)·c=ac+bc
知识梳理
知识点1:用字母表示运算定律或公式。
由于用文字叙述运算定律或公式比较麻烦,有时还说不清,所以可以用字母来表示运算定律或公式。
知识梳理
例题:用字母表示乘法结合律( )。
【解析】乘法结合律指的是:三个数相乘,可以先把前两个数相乘,再同第三个数相乘,也可以先把后两个数相乘,再同第一个数相乘,它们的积不变。准确把握乘法结合律的内容后,可以选择喜欢的字母表示,如(a b)c=a(b c)。
【方法小结】在用字母表示运算定律时,通常用字母a、b、c表示。
(a b)c=a(b c)
知识梳理
知识点2:在用字母表示数中省略乘号。
在用字母表示数时,字母与数字相乘可以乘略乘号或写成 ·,并要把数字放到字母前面;当两个相同的数字或字母相乘时要写成平方的形成,如a a就要写成a ,读作a的平方。
知识梳理
例题:长方形的长是15米,宽是3米,求这个长方形的周长和面积。(a表示长,b表示宽,先写出字母公式,再计算)
【解析】根据长方形的周长=(长+宽)×2 ,面积=长×宽,可以根据字母写出长方形的周长和面积,分别为c=2(a+b)和s=ab,然后再进行计算。
答案:c=2(a+b)=2×(15+3)=36(米)s=ab=15×3=45(平方米)。
【方法小结】在运用字母公式进行计算时,代入的数字要与字母表示的意义一一对应。
知识梳理
【小练习】判断题。
(1)q×1=q ( )
(2)4+a=4a ( )
(3)10×2=10 ( )
(4)8×2=82 ( )
√
×
×
×
课堂作业
1 . 公正的小判官。
(1)a 和2a意义一样。 ( )
(2)a+3可以写成3a。 ( )
(3)a×4可以写成4a。 ( )
(4)5×8的乘号可以省略不写。 ( )
(5)b×2×c写作2bc ( )
×
×
√
×
√
课堂作业
2 . 想一想,填一填。
(1)b与21的和是( ),积是( )
(2)比c少3.2的数是( )
(3)每盒装5块月饼,c盒装( )块月饼。
(4)5本故事书x元,平均每本故事书( )元
(5)淘气今年f岁,爸爸比他大28岁,爸爸今年( )岁。
b+21
21b
c-3.2
5c
x÷5
28+f
课堂练习
3 . 冬冬去超市购物。
食品 牛奶 面包 巧克力
单价 a 元 3元 b 元
(1)一瓶牛奶和一块巧克力( )元。
(2)一块巧克力比一只面包多( )元。
(3)买10瓶牛奶( )元。
(4)80元可以买巧克力( )块。
a+b
b-3
10a
80÷b
课堂练习
4 . 一块平行四边形的菜地,底是6米,高是8米,这块菜地的面积是多少?
答案:S = ah = 6×8 = 4 8(平方米)
(1)a+2.6= + ;b×15= ×
(2)n×8×1.25= ×( × )
(3)(12+16)×c= × + ×
(4)168-35-65= -( + )
课后作业
1 . 根据运算定律填空。
2.6
a
15
b
n
8
1.25
12
c
16
c
168
35
65
课后作业
2 . 用含有字母的式子表示下面各题的数量关系。
(1)在一个三角形中,∠1=a°,∠2=b°,用含有字母的式子表示∠3的度数。
(2)在一个等腰三角形中,底角是a°,用含有字母的式子表示顶角的度数。
答案:180°-a°-b°
答案:180°-2a°
课后作业
2 . 用含有字母的式子表示下面各题的数量关系。
(3)一个正方形的周长是C,用含有字母的式子表示这个正方形的边长。
答案:C÷4
(4)比x的5倍多20的数。
答案:5x+20
(5)比x多20的数是5的多少倍?
答案:(x+20)÷5
3 . 根据公式进行计算。
课后作业
(1)一个长方形长是15分米宽是8分米,求面积?
答案:15×8=120(平方分米)
(2)一个正方形边长是12厘米,求面积?
答案:12×12=144(平方厘米)
(3)一个长方形长是15厘米,宽是6厘米,求周长?
答案:(15+6)×2=42(厘米)
4 . 青青林场栽了梧桐树和雪松各x排,已知梧桐树每排12棵,雪松每排14棵。
课后作业
(1)栽梧桐树和雪松共多少棵?
答案:(12+14)x
(2)当x=20时,青青林场一共有多少棵梧桐树和雪松?
答案:(12+14)×20=520棵
课后作业
5 . 一辆汽车,每小时行驶a千米,上午行驶4小时,下午行驶了b小时。一天共行多少千米?
答案:(4+b)a
知识拓展
用简便方法计算下面各题,再用字母表示出简算思路。
278-23.5-6.5 780÷125÷8
=278-(23.5+6.5)
=248 a-b-c=a-(b+c)
=780 ÷(125×8)
=0.78
a÷b÷c=a÷(bc)
