5 圆 第3课时 圆的面积 课件(共20张PPT)-人教版数学六年级上册
文档属性
| 名称 | 5 圆 第3课时 圆的面积 课件(共20张PPT)-人教版数学六年级上册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-25 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
05 圆
1.3 圆的面积
课题引入
每平方米草皮8元 。这个圆形草坪的占地面积是多少平方米呢?
根据图中信息,可以提出什么数学问题?
教学新知
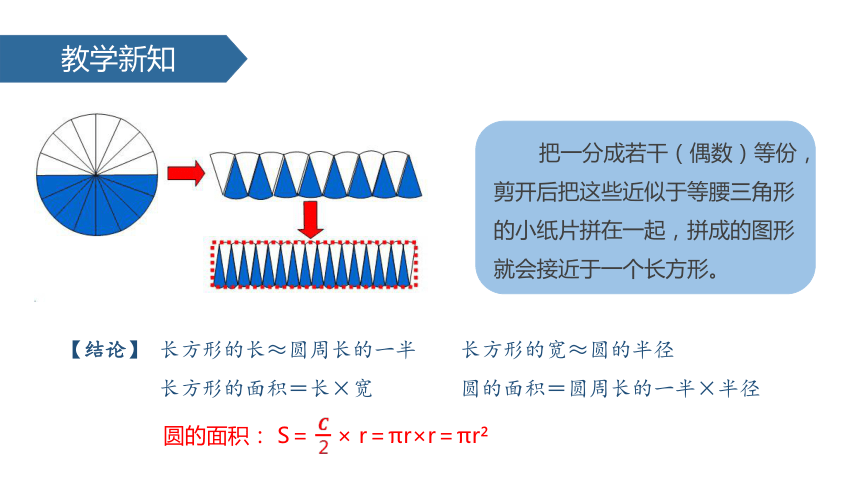
把一分成若干(偶数)等份,剪开后把这些近似于等腰三角形的小纸片拼在一起,拼成的图形就会接近于一个长方形。
【结论】 长方形的长≈圆周长的一半 长方形的宽≈圆的半径
长方形的面积=长×宽 圆的面积=圆周长的一半×半径
圆的面积: S= × r=πr×r=πr
2
应用实践
例题1:有一个圆形草坪的直径是20米,每平方米草皮8元。铺满草皮需要多少钱?
【解析】首先应求出该圆形草坪的面积是多少,再用面积乘以单价就可以得出铺满草坪总共需要多少钱。
半径:r=20÷2=10(米)
草坪面积: 3.14×102=314(平方米)
圆的面积: S=πr
总共需要: 314×8=2512(元)
教学新知
你知道以上图形都是什么形状吗?你还能举例吗?
教学新知
什么是圆环?
两个半径不相等的同心圆,大圆面积比小圆面积多的部分就是圆环。
圆环的面积?
环形面积=外圆面积-内圆的面积
S=πR ﹣πr S=π(R ﹣r )
应用实践
例题1:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm,圆环的面积是多少?
2cm
6cm
S= πR ﹣πr
= 3.14×6 - 3.14×2
= 113.04 - 12.56
= 100.48(cm )
S= π(R ﹣r )
= 3.14×(6 -2 )
= 3.14×32
=100.48(cm )
教学新知
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计(如图所示),图中的两个圆半径都是1米,你能求出正方形和圆之间部分的面积吗?
教学新知
“外方内圆”面积的计算
正方形边长:1×2 = 2(米)
正方形面积:2×2 = 4(平方米)
内圆面积:3.14×1 = 3.14 (平方米)
外方内圆的面积:4 – 3.14 = 0.86(平方米)
“外圆内方”面积的计算
圆的直径:1×2 = 2(米)
正方形面积: ×(2×1)×2 = 2(平方米)
内圆面积:3.14×1 = 3.14 (平方米)
外圆内方的面积:3.14 – 2= 1.14(平方米)
1
2
【解析】“外方内圆”是外面正方形的面积减去里面圆形的面积,圆的直径就是正方形的边长。“外圆内方”是外面圆形的面积减去里面正方形的面积,可将里面的正方形看做两个三角形的面积之和,圆的直径为三角形的底,圆的半径为三角形的高。
拓展运用
1 . 图中的大圆半径等于小圆的直径,求阴影部分的面积。
6 cm
大圆面积: S=πr =3.14 ×6 = 113.04 cm
小圆半径: r=6÷2=3 cm
小圆面积: S=πr = 3.14×3 = 28.26 cm
阴影面积: 113.04 – 28.26 = 84.78 cm
拓展运用
2 . 一个运动场(如图所示),两端是半圆形,中间是长方形,这个运动场周长是多少米?面积是多少平方米?
100 m
32 m
O
长方形的宽:32×2= 64(米)
长方形的面积:100×64= 6400(平方米)
两个半圆面积:3.14×32 =3215.36(平方米)
运动场面积: 6400+3215.36 =9615.36(平方米)
两个半圆弧周长:2×3.14×32 = 200.96(米)
长方形两条长边长:100×2 = 200(米)
运动场周长:200.96+200 = 400.96(米)
知识要点
2. 圆环的面积:外圆面积 - 内圆的面积
即:S=πR ﹣πr 或 S=π(R ﹣r )
1. 圆的面积:S= × r=πr×r=πr
2
3. 外方内圆:正方形面积 - 圆形面积
外圆内方:圆形面积 - 正方形面积
知识梳理
知识点 1:圆的面积
π ≈ . S=πr
例:学校修一个圆形花坛,每平方米造价50元。当花坛修好以后,学校付给施工队700元,施工队找了72元。你知道这个圆形花坛的半径吗?
实际共用:700-72=628(元)
花坛面积:628÷50=12.56(平方米)
S=πr =12.56
r =12.56 ÷3.14=4 r=2 (米)
【解析】要求圆形花坛的半径,首先要知道圆它的面积。从支付的工钱可以得知修了多少平方米的花坛,再从花坛的面积去求花坛的半径。
知识梳理
知识点 2:圆环的面积
圆环面积=外圆面积-内圆的面积
即:S=πR ﹣πr 或 S=π(R ﹣r )
例:幸福小区有一个圆形的花坛,直径为6米,周围用健身石铺了一条宽2米的小路,这条小路的面积是多少平方米?
内圆半径:6÷2=3(米)
外圆半径:3+2= 5(米)
小路面积:3.14×5 -3.14×3 =50.24(平方米)
【解析】求这条小路的面积其实就是求圆环的面积。根据圆环=面积外圆面积-内圆面积的公式就可进行计算。
知识点 3:“外方内圆”和“外圆内方”的面积
知识梳理
外方内圆:正方形面积 - 圆形面积
外圆内方:圆形面积 - 正方形面积
例:在每个正方形中分别做一个最大的圆,并完成下表。
1cm
4cm
9cm
16cm
0.785cm
3.14cm
7.065cm
12.56cm
40:31.4
40:31.4
40:31.4
40:31.4
课堂练习
1 . 填空
(1)( )提出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆全体而无所失矣。”这个伟大的数学思想。
(2)把一个圆平均分成若干份,然后把它剪开,可以拼成一个近似( )的图形,这个( )的长等于圆的( ),宽就是圆的( )。
(3)一个圆的半径是1米,这个圆的直径是( )米,周长是( )米,面积是( )平方米。
刘徽
长方形
长方形
圆周长的一半
半径
2
6.28
3.14
课堂练习
(4)一个圆环,内圆的周长是9.42厘米,环宽是2厘米,内圆半径是( )厘米,外圆半径是( )厘米。
(5)一张长方形的纸,长6厘米,宽4厘米,把它剪成一个最大的圆,这个圆的半径是( )厘米,周长是( )厘米,面积是( )平方厘米。
(6)圆的半径扩大2倍,周长扩大( )倍,面积扩大( )倍。
1.5
3.5
2
12.56
12.56
2
4
课堂练习
2 . 判断
(1)直径相等的两个圆,面积一定相等。 ( )
(2)圆的半径是3厘米,它的周长和面积相等。 ( )
(3)两个半圆可以拼成一个整圆。 ( )
(4)圆的周长越长,半径越长,面积也越大。 ( )
×
×
课堂练习
3. 选择
(1)周长相等的长方形、正方形、三角形和圆,哪个的面积最大?( )
A. 长方形 B. 正方形 C. 三角形 D. 圆
(2)圆的半径从1厘米增加到2厘米,圆的面积增加了几平方厘米?( )
A. 1 B. 2 C. 3 D. 3π
(3)若A.B两个圆的直径比是2:1,则它们的面积比是多少?( )
A. 2 : 4 B. 4 : 1 C. 1 : 2 D. 1 : 4
D
D
B
课堂练习
4 . 解决问题
(1)一个直径是4米的圆形花坛种上玫瑰花。一平方米只能种5株,这个圆形花坛大约能种多少株?
(2)一种环形零件,外圆半径8厘米,内圆半径6厘米,它的截面面积是多少平方厘米?
3.14×8 - 3.14×6 =87.92(平方厘米)
面积:3.14×2 =12.56(平方米) 12.56×5=62.8≈63(株)
半径:4÷2=2(米)
05 圆
1.3 圆的面积
课题引入
每平方米草皮8元 。这个圆形草坪的占地面积是多少平方米呢?
根据图中信息,可以提出什么数学问题?
教学新知
把一分成若干(偶数)等份,剪开后把这些近似于等腰三角形的小纸片拼在一起,拼成的图形就会接近于一个长方形。
【结论】 长方形的长≈圆周长的一半 长方形的宽≈圆的半径
长方形的面积=长×宽 圆的面积=圆周长的一半×半径
圆的面积: S= × r=πr×r=πr
2
应用实践
例题1:有一个圆形草坪的直径是20米,每平方米草皮8元。铺满草皮需要多少钱?
【解析】首先应求出该圆形草坪的面积是多少,再用面积乘以单价就可以得出铺满草坪总共需要多少钱。
半径:r=20÷2=10(米)
草坪面积: 3.14×102=314(平方米)
圆的面积: S=πr
总共需要: 314×8=2512(元)
教学新知
你知道以上图形都是什么形状吗?你还能举例吗?
教学新知
什么是圆环?
两个半径不相等的同心圆,大圆面积比小圆面积多的部分就是圆环。
圆环的面积?
环形面积=外圆面积-内圆的面积
S=πR ﹣πr S=π(R ﹣r )
应用实践
例题1:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm,圆环的面积是多少?
2cm
6cm
S= πR ﹣πr
= 3.14×6 - 3.14×2
= 113.04 - 12.56
= 100.48(cm )
S= π(R ﹣r )
= 3.14×(6 -2 )
= 3.14×32
=100.48(cm )
教学新知
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计(如图所示),图中的两个圆半径都是1米,你能求出正方形和圆之间部分的面积吗?
教学新知
“外方内圆”面积的计算
正方形边长:1×2 = 2(米)
正方形面积:2×2 = 4(平方米)
内圆面积:3.14×1 = 3.14 (平方米)
外方内圆的面积:4 – 3.14 = 0.86(平方米)
“外圆内方”面积的计算
圆的直径:1×2 = 2(米)
正方形面积: ×(2×1)×2 = 2(平方米)
内圆面积:3.14×1 = 3.14 (平方米)
外圆内方的面积:3.14 – 2= 1.14(平方米)
1
2
【解析】“外方内圆”是外面正方形的面积减去里面圆形的面积,圆的直径就是正方形的边长。“外圆内方”是外面圆形的面积减去里面正方形的面积,可将里面的正方形看做两个三角形的面积之和,圆的直径为三角形的底,圆的半径为三角形的高。
拓展运用
1 . 图中的大圆半径等于小圆的直径,求阴影部分的面积。
6 cm
大圆面积: S=πr =3.14 ×6 = 113.04 cm
小圆半径: r=6÷2=3 cm
小圆面积: S=πr = 3.14×3 = 28.26 cm
阴影面积: 113.04 – 28.26 = 84.78 cm
拓展运用
2 . 一个运动场(如图所示),两端是半圆形,中间是长方形,这个运动场周长是多少米?面积是多少平方米?
100 m
32 m
O
长方形的宽:32×2= 64(米)
长方形的面积:100×64= 6400(平方米)
两个半圆面积:3.14×32 =3215.36(平方米)
运动场面积: 6400+3215.36 =9615.36(平方米)
两个半圆弧周长:2×3.14×32 = 200.96(米)
长方形两条长边长:100×2 = 200(米)
运动场周长:200.96+200 = 400.96(米)
知识要点
2. 圆环的面积:外圆面积 - 内圆的面积
即:S=πR ﹣πr 或 S=π(R ﹣r )
1. 圆的面积:S= × r=πr×r=πr
2
3. 外方内圆:正方形面积 - 圆形面积
外圆内方:圆形面积 - 正方形面积
知识梳理
知识点 1:圆的面积
π ≈ . S=πr
例:学校修一个圆形花坛,每平方米造价50元。当花坛修好以后,学校付给施工队700元,施工队找了72元。你知道这个圆形花坛的半径吗?
实际共用:700-72=628(元)
花坛面积:628÷50=12.56(平方米)
S=πr =12.56
r =12.56 ÷3.14=4 r=2 (米)
【解析】要求圆形花坛的半径,首先要知道圆它的面积。从支付的工钱可以得知修了多少平方米的花坛,再从花坛的面积去求花坛的半径。
知识梳理
知识点 2:圆环的面积
圆环面积=外圆面积-内圆的面积
即:S=πR ﹣πr 或 S=π(R ﹣r )
例:幸福小区有一个圆形的花坛,直径为6米,周围用健身石铺了一条宽2米的小路,这条小路的面积是多少平方米?
内圆半径:6÷2=3(米)
外圆半径:3+2= 5(米)
小路面积:3.14×5 -3.14×3 =50.24(平方米)
【解析】求这条小路的面积其实就是求圆环的面积。根据圆环=面积外圆面积-内圆面积的公式就可进行计算。
知识点 3:“外方内圆”和“外圆内方”的面积
知识梳理
外方内圆:正方形面积 - 圆形面积
外圆内方:圆形面积 - 正方形面积
例:在每个正方形中分别做一个最大的圆,并完成下表。
1cm
4cm
9cm
16cm
0.785cm
3.14cm
7.065cm
12.56cm
40:31.4
40:31.4
40:31.4
40:31.4
课堂练习
1 . 填空
(1)( )提出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆全体而无所失矣。”这个伟大的数学思想。
(2)把一个圆平均分成若干份,然后把它剪开,可以拼成一个近似( )的图形,这个( )的长等于圆的( ),宽就是圆的( )。
(3)一个圆的半径是1米,这个圆的直径是( )米,周长是( )米,面积是( )平方米。
刘徽
长方形
长方形
圆周长的一半
半径
2
6.28
3.14
课堂练习
(4)一个圆环,内圆的周长是9.42厘米,环宽是2厘米,内圆半径是( )厘米,外圆半径是( )厘米。
(5)一张长方形的纸,长6厘米,宽4厘米,把它剪成一个最大的圆,这个圆的半径是( )厘米,周长是( )厘米,面积是( )平方厘米。
(6)圆的半径扩大2倍,周长扩大( )倍,面积扩大( )倍。
1.5
3.5
2
12.56
12.56
2
4
课堂练习
2 . 判断
(1)直径相等的两个圆,面积一定相等。 ( )
(2)圆的半径是3厘米,它的周长和面积相等。 ( )
(3)两个半圆可以拼成一个整圆。 ( )
(4)圆的周长越长,半径越长,面积也越大。 ( )
×
×
课堂练习
3. 选择
(1)周长相等的长方形、正方形、三角形和圆,哪个的面积最大?( )
A. 长方形 B. 正方形 C. 三角形 D. 圆
(2)圆的半径从1厘米增加到2厘米,圆的面积增加了几平方厘米?( )
A. 1 B. 2 C. 3 D. 3π
(3)若A.B两个圆的直径比是2:1,则它们的面积比是多少?( )
A. 2 : 4 B. 4 : 1 C. 1 : 2 D. 1 : 4
D
D
B
课堂练习
4 . 解决问题
(1)一个直径是4米的圆形花坛种上玫瑰花。一平方米只能种5株,这个圆形花坛大约能种多少株?
(2)一种环形零件,外圆半径8厘米,内圆半径6厘米,它的截面面积是多少平方厘米?
3.14×8 - 3.14×6 =87.92(平方厘米)
面积:3.14×2 =12.56(平方米) 12.56×5=62.8≈63(株)
半径:4÷2=2(米)
