1.1 认识三角形(第3课时)(同步课件) 2024-2025学年七年级数学上册同步课堂(鲁教版五四制)
文档属性
| 名称 | 1.1 认识三角形(第3课时)(同步课件) 2024-2025学年七年级数学上册同步课堂(鲁教版五四制) |

|
|
| 格式 | pptx | ||
| 文件大小 | 605.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 09:01:16 | ||
图片预览






文档简介
(共22张PPT)
鲁教版七年级上册数学
第一章 三角形
1.3 认识三角形
学习目标
1.了解三角形的角平分线、中线的概念并掌握其性质,会用工具准确画出三角形的角平分线、中线; (重点)
2.学会用数学知识解决实际问题的能力.(重点)
情境&导入
定义 图示
垂线
线段中点
角平分线
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
A
B
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
O
B
A
情境&导入
如图,用铅笔可以支起一张均匀的三角形卡片.
你知道怎样确定这个点的位置吗?
“重心”
三角形的中线
1—
探索&交流
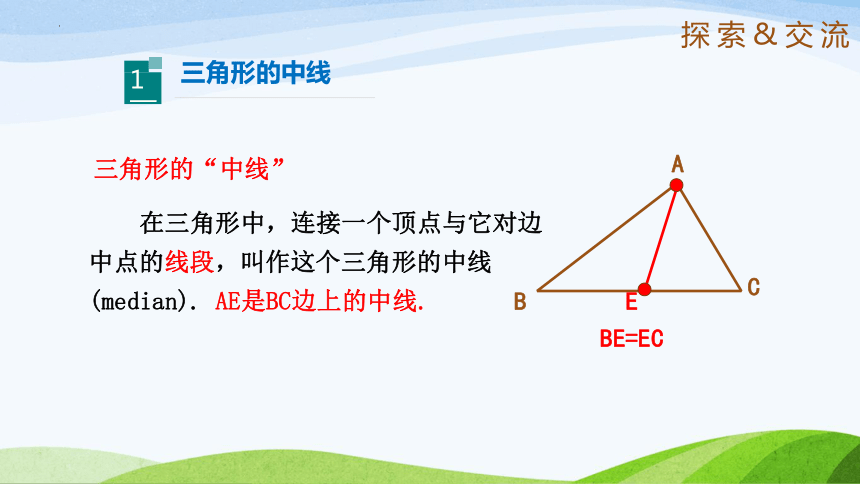
在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线(median). AE是BC边上的中线.
三角形的“中线”
BE=EC
B
C
E
A
探索&交流
三角形的中线有什么特点?
A
B
C
E
(1)AD是△ABC中BC边上的中线.
(2)点D是BC边的中点.
(3)BD=DC或BD= BC或DC= BC
或BD=DC= BC.
想一想
探索&交流
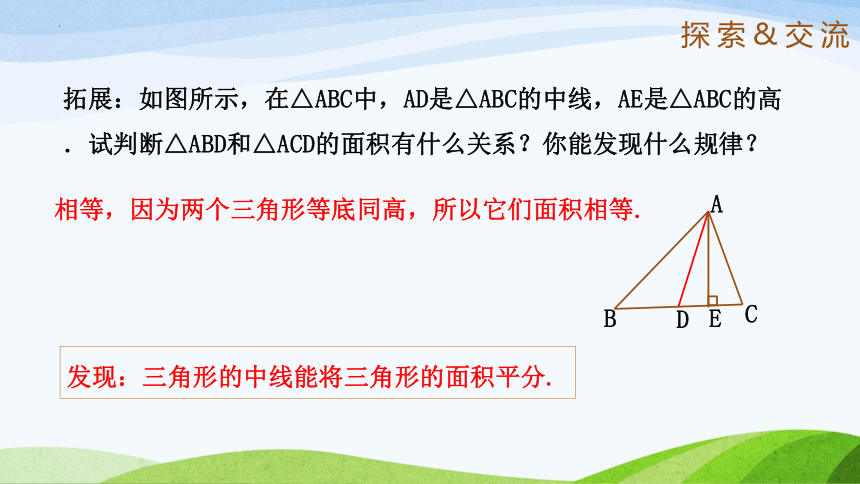
拓展:如图所示,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?你能发现什么规律?
B
C
D
E
A
相等,因为两个三角形等底同高,所以它们面积相等.
发现:三角形的中线能将三角形的面积平分.
探索&交流
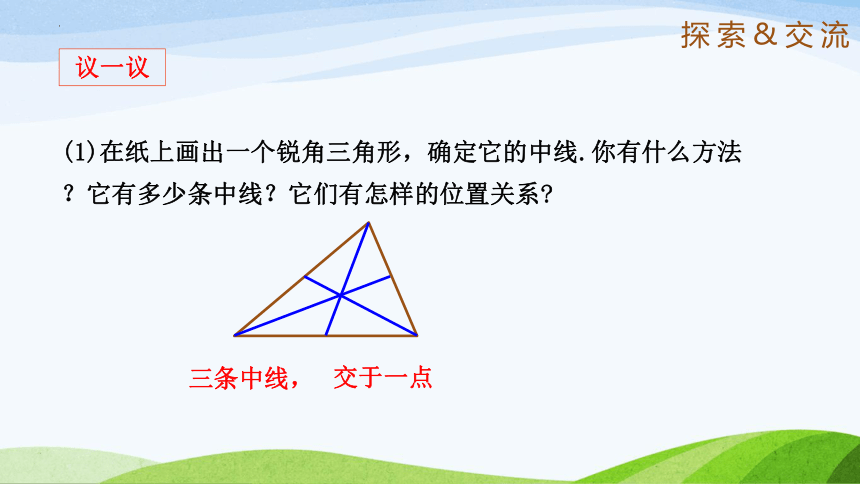
(1)在纸上画出一个锐角三角形,确定它的中线.你有什么方法?它有多少条中线?它们有怎样的位置关系
三条中线,
交于一点
议一议
探索&交流
(2)钝角三角形和直角三角形的中线有几条,它们也有同样的位置关系吗?折一折,画一画,并与同伴交流.
A
C
B
A
B
C
H
H
归纳:三角形的三条中线交于一点,这个交点就是三角形的重心.
典例精析
例1.若AD是△ABC的中线,则下列结论中错误的是( )
A.AB=BC B.BD=DC
C.AD平分BC D.BC=2DC
A
探索&交流
三角形的角平分线
思考 如果现在你手上有一张画着一个三角形的薄纸,你能想办法画出它的一个内角的平分线吗?
你能通过折纸的方法得到它吗
2—
B
A
C
用量角器画最简便,用圆规也能.
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的平分线.
A
B
C
A
D
探索&交流
三角形的角平分线的定义
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
三角形的一个角的平分线叫做三角形的角平分线.这句话对吗?
“三角形的角平分线”是一条线段
A
B
C
D
1
2
∠1 = ∠2
探索&交流
拿出准备好的锐角三角形、钝角三角形和直角三角形纸片各一个,来动手做一做.
做一做
探索&交流
(1) 你能分别画出这三个三角形的三条角平分线吗
(2) 你能用折纸的办法得到它们吗
(3) 在每个三角形中,这三条角平分线之间有怎样的位置关系
探索&交流
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴______=______ =______
∴∠ACB=2______ =2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
三角形的三条角平分线线交于一点
典例精析
例2.如图,AE是 △ABC的角平分线.已知∠B=45°,
∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:因为AE是△ABC的角平分线,
因为 ∠BAC+∠B+∠C=180°,
所以∠BAC=180°-∠B-∠C=180°-45°-60°=75°,所以∠BAE=37.5°.
因为∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
所以∠AEB=37.5°+60°=97.5°.
所以∠CAE=∠BAE= ∠BAC.
随堂练习
练习&巩固
1.(1)线段 AD 是 △ABC 的角平分线,那么∠BAD =________= ________;
(2)线段 AE 是 △ABC 的中线,那么
BE = _____= ___BC.
∠CAD
∠BAC
EC
练习&巩固
D
2.如图,∠1=∠2,∠3=∠4,下列结论错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3= ∠ACB
D.CE是△ABC的角平分线
练习&巩固
3.如图,在△ABC 中,∠A = 50°,∠C = 72°,BD 是△ABC 的一条角平分线,求∠ABD 的度数.
A
B
C
D
解:因为三角形的内角和为180°.
所以∠ABC=180°-∠A-∠C=58°.
又因为BD是△ABC 的角平分线.
所以∠ABD = ∠ABC =29°.
课堂总结
三角形中几条重要线段
角平分线:平分内角且与三角形对边相交的线段.
中线:连接三角形的顶点与对边中点的线段.
鲁教版七年级上册数学
第一章 三角形
1.3 认识三角形
学习目标
1.了解三角形的角平分线、中线的概念并掌握其性质,会用工具准确画出三角形的角平分线、中线; (重点)
2.学会用数学知识解决实际问题的能力.(重点)
情境&导入
定义 图示
垂线
线段中点
角平分线
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
A
B
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
O
B
A
情境&导入
如图,用铅笔可以支起一张均匀的三角形卡片.
你知道怎样确定这个点的位置吗?
“重心”
三角形的中线
1—
探索&交流
在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线(median). AE是BC边上的中线.
三角形的“中线”
BE=EC
B
C
E
A
探索&交流
三角形的中线有什么特点?
A
B
C
E
(1)AD是△ABC中BC边上的中线.
(2)点D是BC边的中点.
(3)BD=DC或BD= BC或DC= BC
或BD=DC= BC.
想一想
探索&交流
拓展:如图所示,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?你能发现什么规律?
B
C
D
E
A
相等,因为两个三角形等底同高,所以它们面积相等.
发现:三角形的中线能将三角形的面积平分.
探索&交流
(1)在纸上画出一个锐角三角形,确定它的中线.你有什么方法?它有多少条中线?它们有怎样的位置关系
三条中线,
交于一点
议一议
探索&交流
(2)钝角三角形和直角三角形的中线有几条,它们也有同样的位置关系吗?折一折,画一画,并与同伴交流.
A
C
B
A
B
C
H
H
归纳:三角形的三条中线交于一点,这个交点就是三角形的重心.
典例精析
例1.若AD是△ABC的中线,则下列结论中错误的是( )
A.AB=BC B.BD=DC
C.AD平分BC D.BC=2DC
A
探索&交流
三角形的角平分线
思考 如果现在你手上有一张画着一个三角形的薄纸,你能想办法画出它的一个内角的平分线吗?
你能通过折纸的方法得到它吗
2—
B
A
C
用量角器画最简便,用圆规也能.
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的平分线.
A
B
C
A
D
探索&交流
三角形的角平分线的定义
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
三角形的一个角的平分线叫做三角形的角平分线.这句话对吗?
“三角形的角平分线”是一条线段
A
B
C
D
1
2
∠1 = ∠2
探索&交流
拿出准备好的锐角三角形、钝角三角形和直角三角形纸片各一个,来动手做一做.
做一做
探索&交流
(1) 你能分别画出这三个三角形的三条角平分线吗
(2) 你能用折纸的办法得到它们吗
(3) 在每个三角形中,这三条角平分线之间有怎样的位置关系
探索&交流
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴______=______ =______
∴∠ACB=2______ =2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
三角形的三条角平分线线交于一点
典例精析
例2.如图,AE是 △ABC的角平分线.已知∠B=45°,
∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:因为AE是△ABC的角平分线,
因为 ∠BAC+∠B+∠C=180°,
所以∠BAC=180°-∠B-∠C=180°-45°-60°=75°,所以∠BAE=37.5°.
因为∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
所以∠AEB=37.5°+60°=97.5°.
所以∠CAE=∠BAE= ∠BAC.
随堂练习
练习&巩固
1.(1)线段 AD 是 △ABC 的角平分线,那么∠BAD =________= ________;
(2)线段 AE 是 △ABC 的中线,那么
BE = _____= ___BC.
∠CAD
∠BAC
EC
练习&巩固
D
2.如图,∠1=∠2,∠3=∠4,下列结论错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3= ∠ACB
D.CE是△ABC的角平分线
练习&巩固
3.如图,在△ABC 中,∠A = 50°,∠C = 72°,BD 是△ABC 的一条角平分线,求∠ABD 的度数.
A
B
C
D
解:因为三角形的内角和为180°.
所以∠ABC=180°-∠A-∠C=58°.
又因为BD是△ABC 的角平分线.
所以∠ABD = ∠ABC =29°.
课堂总结
三角形中几条重要线段
角平分线:平分内角且与三角形对边相交的线段.
中线:连接三角形的顶点与对边中点的线段.
