初中数学中考专区一轮复习:二次函数中的面积计算问题 课件(29张PPT)
文档属性
| 名称 | 初中数学中考专区一轮复习:二次函数中的面积计算问题 课件(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 627.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-26 00:00:00 | ||
图片预览

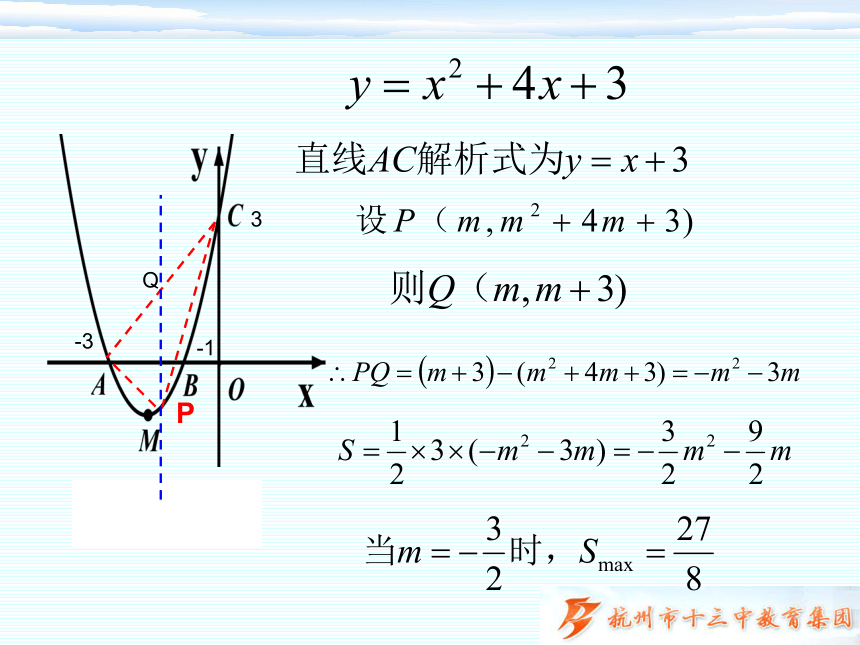




文档简介
(共29张PPT)
二次函数中的面积计算问题
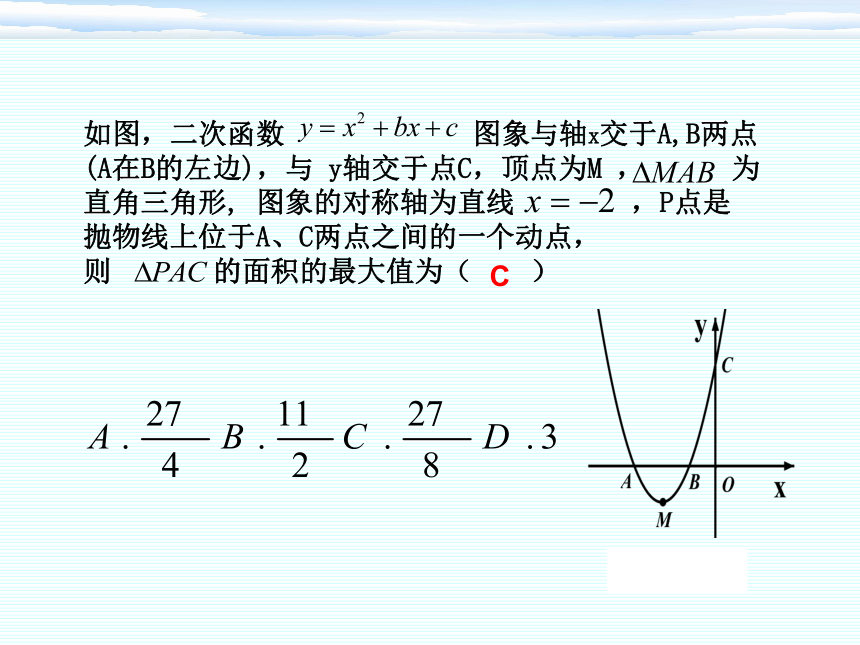
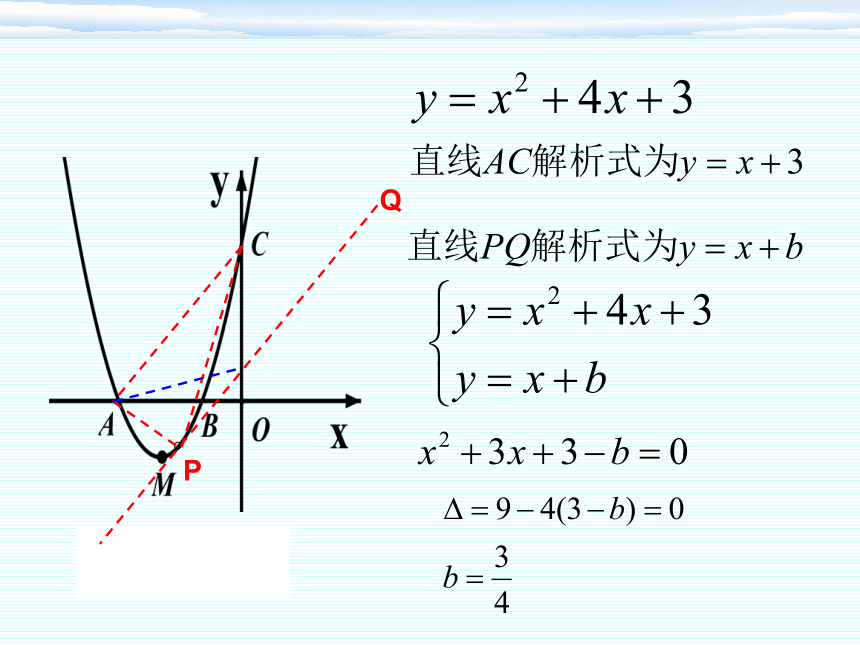
如图,二次函数 图象与轴x交于A,B两点
(A在B的左边),与 y轴交于点C,顶点为M , 为
直角三角形, 图象的对称轴为直线 ,P点是
抛物线上位于A、C两点之间的一个动点,
则 的面积的最大值为( )
C
P
-3
-1
3
Q
P
Q
二次函数中面积问题常见解决方法:
一、运用
二、运用
四、运用分割
三、运用相似
B
C
铅垂高
水平宽
h
a
图2
A
x
C
O
y
A
B
D
1
1
图1
例1:如图1,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),
交y轴于点B。
(1)求抛物线和直线AB的解析式;
(2)求△CAB的铅垂高CD及S△CAB ;
(3)设点P是抛物线(在第一象限内)上的一个动点,
是否存在一点P,使S△PAB=
S△CAB ,若存在,求出P点的坐标;
若不存在,请说明理由。
一、运用
x
C
O
y
A
B
D
1
1
图2
P
(3)设P点的横坐标为x,△PAB的铅垂高为h
A
x
y
B
O
练习1.如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,
将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)如果点P是(2)中的抛物线上的动点,且在x轴的下方,
那么△PAB是否有最大面积?若有,求出此时P点的坐标及
△PAB的最大面积;若没有,请说明理由.
A
x
y
B
O
解:(1)如图1,过点B作BM⊥x轴于M.由旋转性质知OB=OA=2.
∵∠AOB=120°,∴∠BOM=60°.
M
代入坐标易得所求抛物线的解析式为y=
x 2+
x.
C
(3)存在.
直线AB的解析式为y=
x+
x=-1代入直线AB的解析式
∴点C的坐标为(-1, )
P
当x=-
时,△PAB的面积有最大值,最大值为
(2)设经过A、O、B三点的抛物线的解析式为
2.如图,抛物线y=-x 2+bx+c与x轴交于A(1,0),B(-3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,
使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限内是否存在一点P,使△PBC的面积最大?
若存在,求出点P的坐标及△PBC的面积最大值;若不存在,请说明理由.
O
B
A
C
y
x
Q
P
A
B
M
P
O
N
x
y
x=m
y=x
3.如图,已知抛物线y=ax 2+bx-4与直线y=x交于点A、B两点,
A、B的横坐标分别为-1和4。
(1)求此抛物线的解析式。
(2)若平行于y轴的直线x=m(0<m<
+1)与抛物线交于点M,
(3)在(2)的条件下,连接OM、BM,是否存在m的值,使得△BOM
的面积S最大?若存在,请求出m的值,若不存在,请说明理由。
与直线y=x交于点N,交x轴于点P,求线段MN的长(用含m的代数式表示)。
抛物线的解析式为y=x 2-2x-4
MN=MP+PN=-m 2+3m+4
当m=1.5时,S有最大值。
例2. (贵州省遵义市)如图,在平面直角坐标系中,Rt△AOB的
顶点坐标分别为A(0,2),O(0,0),B(4,0),把△AOB绕
点O逆时针方向旋转90°得到△COD(点A转到点C的位置),
抛物线y=ax 2+bx+c(a≠0)经过C、D、B三点.
(1)求抛物线的解析式;
(2)若抛物线的顶点为P,求△PAB的面积;
(3)抛物线上是否存在点M,使△MBC的面积等于△PAB的面积?
若存在,请求出点M的坐标;若不存在,请说明理由.
-3
B
A
x
y
O
2
-1
-1
1
2
3
4
5
-2
1
3
4
5
二.运用
-3
B
A
x
y
O
2
-1
-1
1
2
3
4
5
-2
1
3
4
5
P
(1)∵抛物线经过B(4,0),C(-2,0).
∴可设抛物线的解析式为y=a(x+2)(x-4)
D(0,4)代入上式
(2)S△PAB=S四边形PEOB- S△AOB- S△PEA=6
(3)假设存在这样的点M,其坐标为M(x,y)
∴y=±2.
E
C
练习1.已知二次函数y=x 2+ax+a-2.
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点;
(2)设a <0,当此函数图象与x轴的两个交点的距离为
时,求出此二次函数的解析式;
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,
使得△PAB的面积为
?若存在,求出P点坐标;若不存在,请说明理由.
(1)∵△=a 2-4(a-2)=(a-2)2+4>0
∴不论a为何实数,此函数图象与x轴总有两个交点.
(2)设x1、x2是x 2+ax+a-2=0的两个根
则x1+x2=-a,x1x2=a-2.
∵此函数图象与x轴的两个交点的距离为
∴(x1-x2)2=13.即(x1+x2)2-4x1x2=13.∴(-a)2-4(a-2)=13,
整理得(a+1)(a-5)=0,解得a=-1或a=5.
∵a <0,∴a=-1.
∴此二次函数的解析式为y=x 2-x-3.
(3)设点P的坐标为(x,y)
∴|y|=3,∴y=±3 再得x=-2或x=3;x=0或x=1
P1(-2,3),P2(3,3),P3(0,-3)或P4(1,-3)
B
A
O
Q
P
x
y
2.已知:t1,t2是方程t 2+2t-24=0的两个实数根,且t1<t2,
抛物线y=
x 2+bx+c的图象经过点A(t1,0),B(0,t2).
(3)在(2)的条件下,当□OPAQ的面积为24时,是否存在这样的点P,
使□OPAQ为正方形?若存在,求出P点的坐标;若不存在,说明理由.
(1)求这个抛物线的解析式;
(2)设点P(x,y)是抛物线上一动点,且位于第三象限,四边形OPAQ是以OA为对角线的平行四边形,求□OPAQ的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)当S=24时, P的坐标为(-3,-4)、(-4,-4)
当点P为(-3,-4)时,满足PO=PA,此时,□OPAQ是菱形.
当点P为(-4,-4)时,不满足PO=PA,此时□OPAQ不是菱形
要使□OPAQ为正方形,那么,一定有OA⊥PQ,OA=PQ,此时,点的坐标为(-3,-3),而(-3,-3)不在抛物线上,故不存在这样的点P,使□OPAQ为正方形.
例3:如图,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,
与y轴交于点C(0,4),其中x1,x2是方程x 2-2x-8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,
当△CPE的面积最大时,求点P的坐标;
B
A
y
O
P
E
C
x
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,
使△QBC成为等腰三角形,若存在,请直接写出所有符合条件的
点Q的坐标;若不存在,请说明理由.
解:(1)解方程x2-2x-8=0,得x1=-2,x2=4.
∴A(4,0),B(-2,0).∵抛物线与x轴交于A,B两点,
∴可设抛物线的解析式为y=a(x+2)(x-4)(a≠0)
又∵抛物线与y轴交于点C(0,4),∴a×2×(-4)=4,
三、运用相似
B
A
y
O
P
E
C
x
(2)设点P的坐标为(m,0),过点E作EG⊥x轴于点G,
如图.∵A(4,0),B(-2,0),∴AB=6,BP=m+2.
∵PE∥AC,∴△BPE∽△BAC.
∴S△CPE=S△CBP-S△BPE
∵-2≤m≤4,∴当m=1时,S△CPE有最大值3.
此时点P的坐标为(1,0)
G
练习1.如图,已知抛物线y=ax 2+bx+c与x轴交于A、B两点,与y轴交于点C.
其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)
是方程x 2-5x+4=0的两个根,且抛物线的对称轴是直线x=1.
(1)求A、B、C三点的坐标;
(2)求此抛物线的解析式;
y
x
B
D
O
A
E
C
(3)若点D是线段AB上的一个动点(与点A、B不重合),过点D作
DE∥BC交AC于点E,连结CD,设BD的长为m,△CDE的面积为S,
求S与m的函数关系式,并写出自变量m的取值范围.S是否存在最大值?
若存在,求出最大值并求此时D点坐标;
若不存在,请说明理由.
A(-1,0),B(3,0),C(0,-4).
当m=2时,S有最大值2
D点坐标为(1,0)
2.如图,在梯形ABCD中,DC∥AB,∠A=90°,AD=6厘米,DC=4厘米,
BC的坡度i=3 : 4.动点P从A出发以2厘米/秒的速度沿AB方向向点B运动,
动点Q从点B出发以3厘米/秒的速度沿B→C→D方向向点D运动,两个动点
同时出发,当其中一个动点到达终点时,另一个动点也随之停止.
设动点运动的时间为t秒.
(1)求边BC的长;
(2)当t为何值时,PC与BQ相互平分;
(3)连结PQ ,设△PBQ的面积为y,探求y与t的函数关系式,
求t为何值时,y有最大值?最大值是多少?
C
D
A
B
Q
P
BC=10
t=
0≤ t <
时
C
D
A
B
Q
P
E
F
C
D
A
B
Q
P
E
综合①②,得
当t=3秒时,y有最大值为
厘米2
3. (11·杭州)(本小题满分12分)
图形既关于点O中心对称,又关于直线AC,BD对称,AC=10,
BD=6,已知点E,M是线段AB上的动点(不与端点重合),
点O到EF,MN的距离分别为h1和h2, △OEF与△OGH组成的图形
称为蝶形。
(1)求蝶形面积S的最大值;
(2)当以EH为直径的圆与以MQ为直径的圆重合时,求h1与h2
满足的关系式,并求h2的取值范围。
解:(1)由题意,得四边形ABCD是菱形.
,
即
所以当
时,
.
由
⊿ABD∽⊿AEF
y
x
B
A
O
C
例4.如图,抛物线y=x 2-2x+k与x轴交于A、B两点,与y轴交于
点C(0,-3).(图2、图3为解答备用图)
(1)k= ,点A的坐标为 ,
点B的坐标为 ;
(2)设抛物线y=x 2-2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的
面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线y=x 2-2x+k上求点Q,使△BCQ是以BC为直角边
的直角三角形.
-3
(-1,0)
(3,0)
M
(2)M的坐标为(1,-4).
S四边形ABMC =S△AOC+ S△COM + S△MOB=9
四、运用分割方法
y
x
B
A
O
C
D
(3)设D(m,m 2-2m-3),连结OD,如图.
则0<m<3,m 2-2m-3<0.
S四边形ABDC =S△AOC+ S△COD + S△DOB
四边形ABDC的面积最大
(4)Q1(-2,5)和Q2(1,-4).
O
C
A
B
x
y
M
(图①)
O
C
A
B
x
y
(图②)
练习1.如图①,已知抛物线y=ax 2+bx+3(a≠0)与x轴交于点A(1,0)和
点B(-3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,
使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;
若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,
求四边形BOCE面积的最大值,并求此时E点的坐标.
y=-x 2-2x+3
S四边形BOCE 最大,且最大值为
.
E
D
C
M
y
O
A
B
Q
P
x
2.如图,已知抛物线y=a(x-1)2+
(a≠0)经过点A(-2,0),
抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于x轴的直线
交射线OM于点C,B在x轴正半轴上,连结BC.
(1)求该抛物线的解析式;
(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的
时间为t(s).问:当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?
(3)若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.
设它们的运动的时间为t(s),连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.
当t=6s、5s、4s时,四边形DAOP分别为平行四边形、
直角梯形、等腰梯形
y
x
B
A
O
E
3.练习:如图,△OAB是边长为2的等边三角形,过点A的直线
y=-
x+m与x轴交于点E.
(3)若点P是(2)中求出的抛物线AE段上一动点(不与A、E重合),设四边形OAPE的面积为S,求S的最大值.
(1)求点E的坐标;
(2)求过A、O、E三点的抛物线解析式;
y
x
B
A
O
E
F
G
P
解:(1)过点A作AF⊥x轴于F.
AF=OAsin60°=2
=
.
则OF=OAcos60°=2
=1,
∴A(1,
).
∴m=
∴E(4,0).
(2)设过A、O、E三点的抛物线解析式为
y=ax 2+bx+c∵抛物线过原点,∴c=0.
∴所求抛物线的解析式为y=
x 2+
x.
(3)设P(x0,y0).
S最大=
二次函数中的面积计算问题
如图,二次函数 图象与轴x交于A,B两点
(A在B的左边),与 y轴交于点C,顶点为M , 为
直角三角形, 图象的对称轴为直线 ,P点是
抛物线上位于A、C两点之间的一个动点,
则 的面积的最大值为( )
C
P
-3
-1
3
Q
P
Q
二次函数中面积问题常见解决方法:
一、运用
二、运用
四、运用分割
三、运用相似
B
C
铅垂高
水平宽
h
a
图2
A
x
C
O
y
A
B
D
1
1
图1
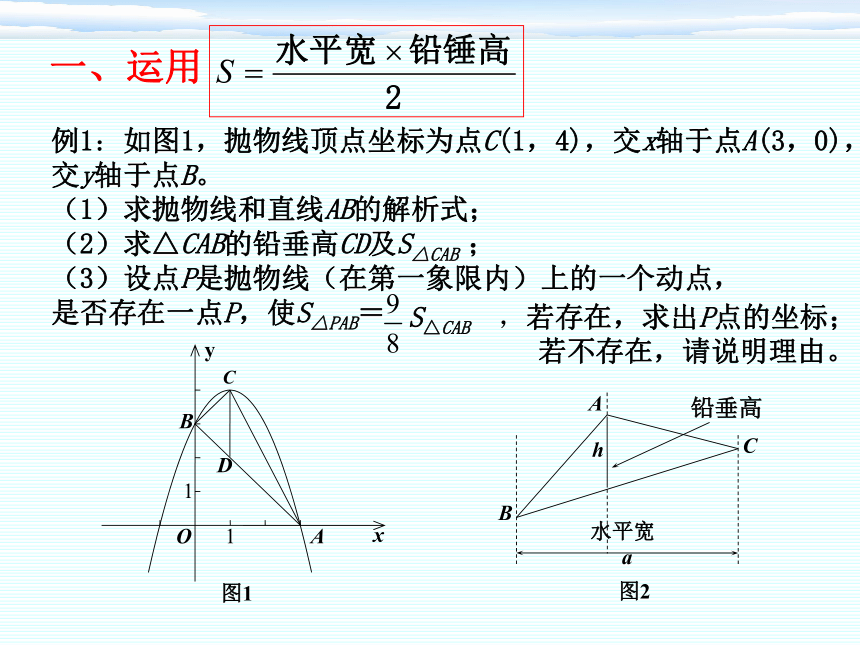
例1:如图1,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),
交y轴于点B。
(1)求抛物线和直线AB的解析式;
(2)求△CAB的铅垂高CD及S△CAB ;
(3)设点P是抛物线(在第一象限内)上的一个动点,
是否存在一点P,使S△PAB=
S△CAB ,若存在,求出P点的坐标;
若不存在,请说明理由。
一、运用
x
C
O
y
A
B
D
1
1
图2
P
(3)设P点的横坐标为x,△PAB的铅垂高为h
A
x
y
B
O
练习1.如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,
将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)如果点P是(2)中的抛物线上的动点,且在x轴的下方,
那么△PAB是否有最大面积?若有,求出此时P点的坐标及
△PAB的最大面积;若没有,请说明理由.
A
x
y
B
O
解:(1)如图1,过点B作BM⊥x轴于M.由旋转性质知OB=OA=2.
∵∠AOB=120°,∴∠BOM=60°.
M
代入坐标易得所求抛物线的解析式为y=
x 2+
x.
C
(3)存在.
直线AB的解析式为y=
x+
x=-1代入直线AB的解析式
∴点C的坐标为(-1, )
P
当x=-
时,△PAB的面积有最大值,最大值为
(2)设经过A、O、B三点的抛物线的解析式为
2.如图,抛物线y=-x 2+bx+c与x轴交于A(1,0),B(-3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,
使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限内是否存在一点P,使△PBC的面积最大?
若存在,求出点P的坐标及△PBC的面积最大值;若不存在,请说明理由.
O
B
A
C
y
x
Q
P
A
B
M
P
O
N
x
y
x=m
y=x
3.如图,已知抛物线y=ax 2+bx-4与直线y=x交于点A、B两点,
A、B的横坐标分别为-1和4。
(1)求此抛物线的解析式。
(2)若平行于y轴的直线x=m(0<m<
+1)与抛物线交于点M,
(3)在(2)的条件下,连接OM、BM,是否存在m的值,使得△BOM
的面积S最大?若存在,请求出m的值,若不存在,请说明理由。
与直线y=x交于点N,交x轴于点P,求线段MN的长(用含m的代数式表示)。
抛物线的解析式为y=x 2-2x-4
MN=MP+PN=-m 2+3m+4
当m=1.5时,S有最大值。
例2. (贵州省遵义市)如图,在平面直角坐标系中,Rt△AOB的
顶点坐标分别为A(0,2),O(0,0),B(4,0),把△AOB绕
点O逆时针方向旋转90°得到△COD(点A转到点C的位置),
抛物线y=ax 2+bx+c(a≠0)经过C、D、B三点.
(1)求抛物线的解析式;
(2)若抛物线的顶点为P,求△PAB的面积;
(3)抛物线上是否存在点M,使△MBC的面积等于△PAB的面积?
若存在,请求出点M的坐标;若不存在,请说明理由.
-3
B
A
x
y
O
2
-1
-1
1
2
3
4
5
-2
1
3
4
5
二.运用
-3
B
A
x
y
O
2
-1
-1
1
2
3
4
5
-2
1
3
4
5
P
(1)∵抛物线经过B(4,0),C(-2,0).
∴可设抛物线的解析式为y=a(x+2)(x-4)
D(0,4)代入上式
(2)S△PAB=S四边形PEOB- S△AOB- S△PEA=6
(3)假设存在这样的点M,其坐标为M(x,y)
∴y=±2.
E
C
练习1.已知二次函数y=x 2+ax+a-2.
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点;
(2)设a <0,当此函数图象与x轴的两个交点的距离为
时,求出此二次函数的解析式;
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,
使得△PAB的面积为
?若存在,求出P点坐标;若不存在,请说明理由.
(1)∵△=a 2-4(a-2)=(a-2)2+4>0
∴不论a为何实数,此函数图象与x轴总有两个交点.
(2)设x1、x2是x 2+ax+a-2=0的两个根
则x1+x2=-a,x1x2=a-2.
∵此函数图象与x轴的两个交点的距离为
∴(x1-x2)2=13.即(x1+x2)2-4x1x2=13.∴(-a)2-4(a-2)=13,
整理得(a+1)(a-5)=0,解得a=-1或a=5.
∵a <0,∴a=-1.
∴此二次函数的解析式为y=x 2-x-3.
(3)设点P的坐标为(x,y)
∴|y|=3,∴y=±3 再得x=-2或x=3;x=0或x=1
P1(-2,3),P2(3,3),P3(0,-3)或P4(1,-3)
B
A
O
Q
P
x
y
2.已知:t1,t2是方程t 2+2t-24=0的两个实数根,且t1<t2,
抛物线y=
x 2+bx+c的图象经过点A(t1,0),B(0,t2).
(3)在(2)的条件下,当□OPAQ的面积为24时,是否存在这样的点P,
使□OPAQ为正方形?若存在,求出P点的坐标;若不存在,说明理由.
(1)求这个抛物线的解析式;
(2)设点P(x,y)是抛物线上一动点,且位于第三象限,四边形OPAQ是以OA为对角线的平行四边形,求□OPAQ的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)当S=24时, P的坐标为(-3,-4)、(-4,-4)
当点P为(-3,-4)时,满足PO=PA,此时,□OPAQ是菱形.
当点P为(-4,-4)时,不满足PO=PA,此时□OPAQ不是菱形
要使□OPAQ为正方形,那么,一定有OA⊥PQ,OA=PQ,此时,点的坐标为(-3,-3),而(-3,-3)不在抛物线上,故不存在这样的点P,使□OPAQ为正方形.
例3:如图,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,
与y轴交于点C(0,4),其中x1,x2是方程x 2-2x-8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,
当△CPE的面积最大时,求点P的坐标;
B
A
y
O
P
E
C
x
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,
使△QBC成为等腰三角形,若存在,请直接写出所有符合条件的
点Q的坐标;若不存在,请说明理由.
解:(1)解方程x2-2x-8=0,得x1=-2,x2=4.
∴A(4,0),B(-2,0).∵抛物线与x轴交于A,B两点,
∴可设抛物线的解析式为y=a(x+2)(x-4)(a≠0)
又∵抛物线与y轴交于点C(0,4),∴a×2×(-4)=4,
三、运用相似
B
A
y
O
P
E
C
x
(2)设点P的坐标为(m,0),过点E作EG⊥x轴于点G,
如图.∵A(4,0),B(-2,0),∴AB=6,BP=m+2.
∵PE∥AC,∴△BPE∽△BAC.
∴S△CPE=S△CBP-S△BPE
∵-2≤m≤4,∴当m=1时,S△CPE有最大值3.
此时点P的坐标为(1,0)
G
练习1.如图,已知抛物线y=ax 2+bx+c与x轴交于A、B两点,与y轴交于点C.
其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)
是方程x 2-5x+4=0的两个根,且抛物线的对称轴是直线x=1.
(1)求A、B、C三点的坐标;
(2)求此抛物线的解析式;
y
x
B
D
O
A
E
C
(3)若点D是线段AB上的一个动点(与点A、B不重合),过点D作
DE∥BC交AC于点E,连结CD,设BD的长为m,△CDE的面积为S,
求S与m的函数关系式,并写出自变量m的取值范围.S是否存在最大值?
若存在,求出最大值并求此时D点坐标;
若不存在,请说明理由.
A(-1,0),B(3,0),C(0,-4).
当m=2时,S有最大值2
D点坐标为(1,0)
2.如图,在梯形ABCD中,DC∥AB,∠A=90°,AD=6厘米,DC=4厘米,
BC的坡度i=3 : 4.动点P从A出发以2厘米/秒的速度沿AB方向向点B运动,
动点Q从点B出发以3厘米/秒的速度沿B→C→D方向向点D运动,两个动点
同时出发,当其中一个动点到达终点时,另一个动点也随之停止.
设动点运动的时间为t秒.
(1)求边BC的长;
(2)当t为何值时,PC与BQ相互平分;
(3)连结PQ ,设△PBQ的面积为y,探求y与t的函数关系式,
求t为何值时,y有最大值?最大值是多少?
C
D
A
B
Q
P
BC=10
t=
0≤ t <
时
C
D
A
B
Q
P
E
F
C
D
A
B
Q
P
E
综合①②,得
当t=3秒时,y有最大值为
厘米2
3. (11·杭州)(本小题满分12分)
图形既关于点O中心对称,又关于直线AC,BD对称,AC=10,
BD=6,已知点E,M是线段AB上的动点(不与端点重合),
点O到EF,MN的距离分别为h1和h2, △OEF与△OGH组成的图形
称为蝶形。
(1)求蝶形面积S的最大值;
(2)当以EH为直径的圆与以MQ为直径的圆重合时,求h1与h2
满足的关系式,并求h2的取值范围。
解:(1)由题意,得四边形ABCD是菱形.
,
即
所以当
时,
.
由
⊿ABD∽⊿AEF
y
x
B
A
O
C
例4.如图,抛物线y=x 2-2x+k与x轴交于A、B两点,与y轴交于
点C(0,-3).(图2、图3为解答备用图)
(1)k= ,点A的坐标为 ,
点B的坐标为 ;
(2)设抛物线y=x 2-2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的
面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线y=x 2-2x+k上求点Q,使△BCQ是以BC为直角边
的直角三角形.
-3
(-1,0)
(3,0)
M
(2)M的坐标为(1,-4).
S四边形ABMC =S△AOC+ S△COM + S△MOB=9
四、运用分割方法
y
x
B
A
O
C
D
(3)设D(m,m 2-2m-3),连结OD,如图.
则0<m<3,m 2-2m-3<0.
S四边形ABDC =S△AOC+ S△COD + S△DOB
四边形ABDC的面积最大
(4)Q1(-2,5)和Q2(1,-4).
O
C
A
B
x
y
M
(图①)
O
C
A
B
x
y
(图②)
练习1.如图①,已知抛物线y=ax 2+bx+3(a≠0)与x轴交于点A(1,0)和
点B(-3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,
使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;
若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,
求四边形BOCE面积的最大值,并求此时E点的坐标.
y=-x 2-2x+3
S四边形BOCE 最大,且最大值为
.
E
D
C
M
y
O
A
B
Q
P
x
2.如图,已知抛物线y=a(x-1)2+
(a≠0)经过点A(-2,0),
抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于x轴的直线
交射线OM于点C,B在x轴正半轴上,连结BC.
(1)求该抛物线的解析式;
(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的
时间为t(s).问:当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?
(3)若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.
设它们的运动的时间为t(s),连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.
当t=6s、5s、4s时,四边形DAOP分别为平行四边形、
直角梯形、等腰梯形
y
x
B
A
O
E
3.练习:如图,△OAB是边长为2的等边三角形,过点A的直线
y=-
x+m与x轴交于点E.
(3)若点P是(2)中求出的抛物线AE段上一动点(不与A、E重合),设四边形OAPE的面积为S,求S的最大值.
(1)求点E的坐标;
(2)求过A、O、E三点的抛物线解析式;
y
x
B
A
O
E
F
G
P
解:(1)过点A作AF⊥x轴于F.
AF=OAsin60°=2
=
.
则OF=OAcos60°=2
=1,
∴A(1,
).
∴m=
∴E(4,0).
(2)设过A、O、E三点的抛物线解析式为
y=ax 2+bx+c∵抛物线过原点,∴c=0.
∴所求抛物线的解析式为y=
x 2+
x.
(3)设P(x0,y0).
S最大=
同课章节目录
