人教版八年级上册 13.1.1 轴对称 说课课件(25张PPT)
文档属性
| 名称 | 人教版八年级上册 13.1.1 轴对称 说课课件(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-26 11:26:00 | ||
图片预览





文档简介
(共25张PPT)
13.1 轴对称(第1课时)
目录
内容和内容解析
目标和目标解析
教学设计说明
问题诊断及分析
教学过程呈现
选自人教版八年级上册第十三章《13.1轴对称》第1课时,主要学习轴对称图形和图形的轴对称的概念,轴对称的性质,线段垂直平分线的概念.
教学内容
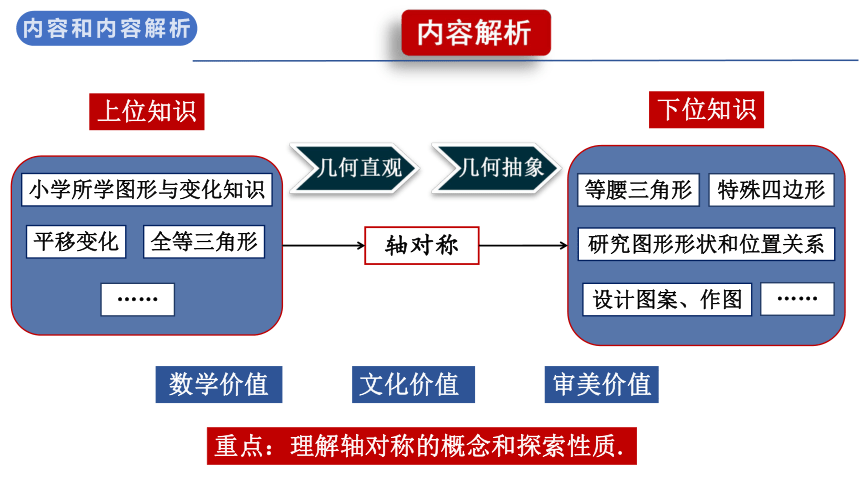
内容和内容解析
轴对称
研究图形形状和位置关系
等腰三角形
……
特殊四边形
小学所学图形与变化知识
上位知识
下位知识
平移变化
全等三角形
设计图案、作图
……
几何直观
几何抽象
重点:理解轴对称的概念和探索性质.
内容和内容解析
内容解析
文化价值
审美价值
数学价值
单元目标
通过实例抽象形成轴对称(图形)的概念,再探索性质,简单作图,借助轴对称,探索等腰三角形的性质和判定,进一步来研究等边三角形,发展学生的抽象能力、推理能力、几何直观及空间观念.
目标和目标解析
目标1
目标和目标解析
由生活中常见图形抽象出轴对称图形和成轴对称的概念,发展抽象能力,学会用数学的眼光观察现实世界.
目标2
理解轴对称图形和成轴对称间的关系,分析其性质,发展推理能力,学会用数学的思维分析数学问题的素养.
目标3
了解线段垂直平分线的概念,学会用数学语言表达轴对称的性质,初步感受轴对称在现实生活中的运用.
课时目标
添加标题
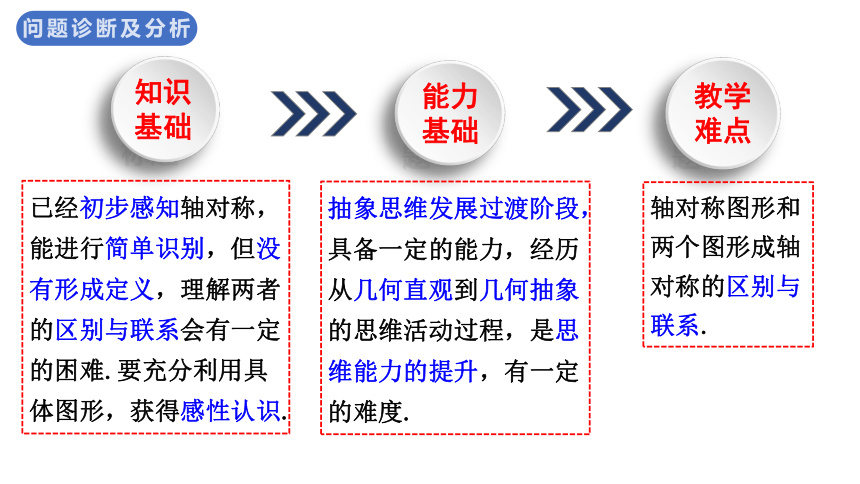
知识基础
添加标题
能力基础
添加标题
教学难点
已经初步感知轴对称,能进行简单识别,但没有形成定义,理解两者的区别与联系会有一定的困难.要充分利用具体图形,获得感性认识.
抽象思维发展过渡阶段,具备一定的能力,经历从几何直观到几何抽象的思维活动过程,是思维能力的提升,有一定的难度.
轴对称图形和两个图形成轴对称的区别与联系.
问题诊断及分析
教学过程呈现
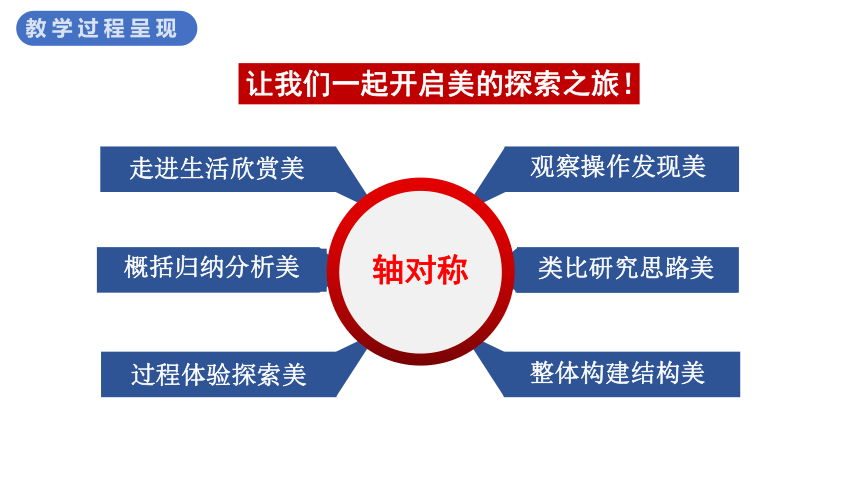
让我们一起开启美的探索之旅!
概括归纳分析美
过程体验探索美
观察操作发现美
类比研究思路美
整体构建结构美
轴对称
走进生活欣赏美
走进生活欣赏美
问题1 观察下面美丽的图案,它们有什么共同的特征呢?
教学过程呈现
追问1:给你1张彩色A4纸,能否剪出如下图那样美丽的对称图形吗?
设计意图:引导学生在欣赏美和动手操作的过程中,发现轴对称的特征,体验对称轴是条直线,逐步养成用数学的眼光观察世界的习惯,发展几何直观能力,提升学习兴趣.促进目标(1)(3)的达成.
走进生活欣赏美
教学过程呈现
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
追问2:根据特征,你能给这类几何图形下一个定义吗
追问3:你能举出一些生活中轴对称图形的例子吗
走进生活欣赏美
教学过程呈现
练习1 下列图形是轴对称图形吗?如果是,请指出它的对称轴.
追问:你是如何判断一个图形是轴对称图形的呢?
走进生活欣赏美
观察
找线
折叠
判断
教学过程呈现
等腰三角形
长方形
等边三角形
圆
设计意图:基于特征归纳,给出直观描述,形成轴对称图形的概念,通过举例、练习、方法归纳,对本质特征进行再认识,从感性逐步上升到理性认识,发展抽象能力、几何直观,同时感受对称现象的广泛存在性,促进目标(1)的达成.
走进生活欣赏美
练习2 我们已经认识了很多几何图形,你能举一些轴对称图形的例子吗?
角
线段
正方形
……
教学过程呈现
追问1:你能给满足这种特殊关系的两个图形下一个定义吗
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
观察操作发现美
教学过程呈现
问题2 请把剪的轴对称图形沿折痕剪开,如图摆放,它们有什么关系呢?
练习3 如图所示的每幅图形中的两个图案是轴对称的吗?如果是,找出它们的对称轴,并找出一对对称点.
追问:你能再举出一些两个图形成轴对称的例子吗
设计意图:通过动手操作和动画演示,发现关系,进而概括得到两个图形成轴对称的概念,实现已有知识的正迁移,为下一步区分两个概念作好铺垫,进一步发展抽象能力与空间观念,促进目标(1)的达成.
观察操作发现美
教学过程呈现
A
B
C
A
A′
C′
B′
B
C
轴对称图形
两个图形成轴对称
一分为二
合二为一
问题3 轴对称图形和两个图形成轴对称有什么异同呢
概括归纳分析美
追问1:如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图
形全等吗 这两个图形对称吗
追问2:如果把两个成轴对称的图形看成一个整体,是一个轴对称图形吗?
教学过程呈现
轴对称与轴对称图形的区别与联系
轴对称图形 轴对称
图形
区别 一个图形具有的特殊形状 两个全等图形的特殊的位置关系
联系 设计意图:通过操作和归纳,从运动角度和变化观点认识图形,理解轴对称图形和两个图形成轴对称的之间的辩证关系,突破难点,发展学生的抽象概括能力.
概括归纳分析美
轴对称图形
两个图形成轴对称
一分为二
合二为一
教学过程呈现
生活中图形
平移的概念
平移的性质
平移的应用
抽象
问题4 轴对称和平移都是图形变化,你能类比平移的学习历程规划
轴对称的学习思路吗?
生活中图形
轴对称概念
轴对称性质
抽象
轴对称应用
追问:我们应该如何研究轴对称的性质呢?
类比研究思路美
设计意图:类比平移的学习历程,规划轴对称的研究思路、内容和方法.
整体
局部
用点来刻画关系
教学过程呈现
研究对称点与对称轴的关系
追问1:如果再多扎一个孔,重复刚才的做法(如图2),你有什么发现?
追问2:如果重复上面的步骤再多扎一些孔(如图3),上述结论还成立吗
追问3:能用文字语言和符号语言来表示这个性质吗
A
A′
M
P
B
B′
N
N
A
A′
M
P
B
B′
C
C′
问题5 将A4纸对折,用笔尖在纸上扎一个孔,然后展开. 将两孔分别记为点 A,A′, 把折痕抽象成直线 MN,连接AA′,如图1,你有什么发现?
……
A
A′
M
N
P
过程体验探索美
图1
图2
图3
教学过程呈现
追问4:如何找出如图所示轴对称图形的对称轴?
轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
设计意图:从特例出发,用点来刻画关系,再到线、面,反复体验用垂直平分线描述轴对称,让学生经历“四能”的探究过程,使思维由感性到理性、片段到系统,形成问题研究的一般方法,发展概括推理能力,同时也为接下来学习轴对称作图作好铺垫,促进目标(2)(3)的达成.
过程体验探索美
教学过程呈现
问题6 通过本课的探究,我们学习了新的内容,请完成以下问题清单:
(1)本节课学到了哪些知识,体现了哪些思想方法?
整体构建结构美
(2)我们是如何展开轴对称(图形)和性质研究的呢?
生活中图形
轴对称(图形)
定义
性质
抽象
观察
归纳
操作
验证
表达
研究路径
研究方法
归纳
点刻画
运用
教学过程呈现
整体构建结构美
(3)类比平移的研究思路,接下来我们还将研究哪些内容?
设计意图:从多维度进行小结,通过回顾学习历程,归纳概念性质学习的一般方法,领悟抽象、类比迁移等数学思想的运用,整体构建本章研究思路,形成几何变化的知识体系,促进目标(3)的达成.
几何
变化
平移
旋转
定义
性质
应用
线段(垂直平分线)
角(角平分线)
等腰(边)三角形
性质→判定→应用
轴对称
教学过程呈现
问题6 通过本课的探究,我们学习了新的内容,请完成以下问题清单:
动手实践创造美
操作实践:为我校的劳动实践基地设计1个创意标志,要求设计图
为轴对称图形,并用简炼的文字说明你的创意.
书面作业:必做:作业本① 《13.1.1 轴对称》复习巩固
选做:作业本① 《13.1.1 轴对称》综合运用
设计意图:作业形式丰富,分必做、选做题和操作设计,让不同能力层次的学生都能得到发展和提高,进一步体验对称美,增强应用意识和实践能力,提升学习兴趣,促进目标(3)的达成.
教学过程呈现
设计说明
观察、操作、体验,归纳特征,抽象概念.
问题驱动
发展素养
整体构建
类比探究
抽象概念
抽象能力、几何直观、推理能力.
学为中心,问题驱动,设计活动,体验过程.
整体构建,形成几何变化知识体系.
类比平移,用运动变化观点探究性质.
感受轴对称的数学价值和美学价值
教法
学法
思路
理念
目标
谢谢倾听
13.1 轴对称(第1课时)
目录
内容和内容解析
目标和目标解析
教学设计说明
问题诊断及分析
教学过程呈现
选自人教版八年级上册第十三章《13.1轴对称》第1课时,主要学习轴对称图形和图形的轴对称的概念,轴对称的性质,线段垂直平分线的概念.
教学内容
内容和内容解析
轴对称
研究图形形状和位置关系
等腰三角形
……
特殊四边形
小学所学图形与变化知识
上位知识
下位知识
平移变化
全等三角形
设计图案、作图
……
几何直观
几何抽象
重点:理解轴对称的概念和探索性质.
内容和内容解析
内容解析
文化价值
审美价值
数学价值
单元目标
通过实例抽象形成轴对称(图形)的概念,再探索性质,简单作图,借助轴对称,探索等腰三角形的性质和判定,进一步来研究等边三角形,发展学生的抽象能力、推理能力、几何直观及空间观念.
目标和目标解析
目标1
目标和目标解析
由生活中常见图形抽象出轴对称图形和成轴对称的概念,发展抽象能力,学会用数学的眼光观察现实世界.
目标2
理解轴对称图形和成轴对称间的关系,分析其性质,发展推理能力,学会用数学的思维分析数学问题的素养.
目标3
了解线段垂直平分线的概念,学会用数学语言表达轴对称的性质,初步感受轴对称在现实生活中的运用.
课时目标
添加标题
知识基础
添加标题
能力基础
添加标题
教学难点
已经初步感知轴对称,能进行简单识别,但没有形成定义,理解两者的区别与联系会有一定的困难.要充分利用具体图形,获得感性认识.
抽象思维发展过渡阶段,具备一定的能力,经历从几何直观到几何抽象的思维活动过程,是思维能力的提升,有一定的难度.
轴对称图形和两个图形成轴对称的区别与联系.
问题诊断及分析
教学过程呈现
让我们一起开启美的探索之旅!
概括归纳分析美
过程体验探索美
观察操作发现美
类比研究思路美
整体构建结构美
轴对称
走进生活欣赏美
走进生活欣赏美
问题1 观察下面美丽的图案,它们有什么共同的特征呢?
教学过程呈现
追问1:给你1张彩色A4纸,能否剪出如下图那样美丽的对称图形吗?
设计意图:引导学生在欣赏美和动手操作的过程中,发现轴对称的特征,体验对称轴是条直线,逐步养成用数学的眼光观察世界的习惯,发展几何直观能力,提升学习兴趣.促进目标(1)(3)的达成.
走进生活欣赏美
教学过程呈现
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
追问2:根据特征,你能给这类几何图形下一个定义吗
追问3:你能举出一些生活中轴对称图形的例子吗
走进生活欣赏美
教学过程呈现
练习1 下列图形是轴对称图形吗?如果是,请指出它的对称轴.
追问:你是如何判断一个图形是轴对称图形的呢?
走进生活欣赏美
观察
找线
折叠
判断
教学过程呈现
等腰三角形
长方形
等边三角形
圆
设计意图:基于特征归纳,给出直观描述,形成轴对称图形的概念,通过举例、练习、方法归纳,对本质特征进行再认识,从感性逐步上升到理性认识,发展抽象能力、几何直观,同时感受对称现象的广泛存在性,促进目标(1)的达成.
走进生活欣赏美
练习2 我们已经认识了很多几何图形,你能举一些轴对称图形的例子吗?
角
线段
正方形
……
教学过程呈现
追问1:你能给满足这种特殊关系的两个图形下一个定义吗
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
观察操作发现美
教学过程呈现
问题2 请把剪的轴对称图形沿折痕剪开,如图摆放,它们有什么关系呢?
练习3 如图所示的每幅图形中的两个图案是轴对称的吗?如果是,找出它们的对称轴,并找出一对对称点.
追问:你能再举出一些两个图形成轴对称的例子吗
设计意图:通过动手操作和动画演示,发现关系,进而概括得到两个图形成轴对称的概念,实现已有知识的正迁移,为下一步区分两个概念作好铺垫,进一步发展抽象能力与空间观念,促进目标(1)的达成.
观察操作发现美
教学过程呈现
A
B
C
A
A′
C′
B′
B
C
轴对称图形
两个图形成轴对称
一分为二
合二为一
问题3 轴对称图形和两个图形成轴对称有什么异同呢
概括归纳分析美
追问1:如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图
形全等吗 这两个图形对称吗
追问2:如果把两个成轴对称的图形看成一个整体,是一个轴对称图形吗?
教学过程呈现
轴对称与轴对称图形的区别与联系
轴对称图形 轴对称
图形
区别 一个图形具有的特殊形状 两个全等图形的特殊的位置关系
联系 设计意图:通过操作和归纳,从运动角度和变化观点认识图形,理解轴对称图形和两个图形成轴对称的之间的辩证关系,突破难点,发展学生的抽象概括能力.
概括归纳分析美
轴对称图形
两个图形成轴对称
一分为二
合二为一
教学过程呈现
生活中图形
平移的概念
平移的性质
平移的应用
抽象
问题4 轴对称和平移都是图形变化,你能类比平移的学习历程规划
轴对称的学习思路吗?
生活中图形
轴对称概念
轴对称性质
抽象
轴对称应用
追问:我们应该如何研究轴对称的性质呢?
类比研究思路美
设计意图:类比平移的学习历程,规划轴对称的研究思路、内容和方法.
整体
局部
用点来刻画关系
教学过程呈现
研究对称点与对称轴的关系
追问1:如果再多扎一个孔,重复刚才的做法(如图2),你有什么发现?
追问2:如果重复上面的步骤再多扎一些孔(如图3),上述结论还成立吗
追问3:能用文字语言和符号语言来表示这个性质吗
A
A′
M
P
B
B′
N
N
A
A′
M
P
B
B′
C
C′
问题5 将A4纸对折,用笔尖在纸上扎一个孔,然后展开. 将两孔分别记为点 A,A′, 把折痕抽象成直线 MN,连接AA′,如图1,你有什么发现?
……
A
A′
M
N
P
过程体验探索美
图1
图2
图3
教学过程呈现
追问4:如何找出如图所示轴对称图形的对称轴?
轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
设计意图:从特例出发,用点来刻画关系,再到线、面,反复体验用垂直平分线描述轴对称,让学生经历“四能”的探究过程,使思维由感性到理性、片段到系统,形成问题研究的一般方法,发展概括推理能力,同时也为接下来学习轴对称作图作好铺垫,促进目标(2)(3)的达成.
过程体验探索美
教学过程呈现
问题6 通过本课的探究,我们学习了新的内容,请完成以下问题清单:
(1)本节课学到了哪些知识,体现了哪些思想方法?
整体构建结构美
(2)我们是如何展开轴对称(图形)和性质研究的呢?
生活中图形
轴对称(图形)
定义
性质
抽象
观察
归纳
操作
验证
表达
研究路径
研究方法
归纳
点刻画
运用
教学过程呈现
整体构建结构美
(3)类比平移的研究思路,接下来我们还将研究哪些内容?
设计意图:从多维度进行小结,通过回顾学习历程,归纳概念性质学习的一般方法,领悟抽象、类比迁移等数学思想的运用,整体构建本章研究思路,形成几何变化的知识体系,促进目标(3)的达成.
几何
变化
平移
旋转
定义
性质
应用
线段(垂直平分线)
角(角平分线)
等腰(边)三角形
性质→判定→应用
轴对称
教学过程呈现
问题6 通过本课的探究,我们学习了新的内容,请完成以下问题清单:
动手实践创造美
操作实践:为我校的劳动实践基地设计1个创意标志,要求设计图
为轴对称图形,并用简炼的文字说明你的创意.
书面作业:必做:作业本① 《13.1.1 轴对称》复习巩固
选做:作业本① 《13.1.1 轴对称》综合运用
设计意图:作业形式丰富,分必做、选做题和操作设计,让不同能力层次的学生都能得到发展和提高,进一步体验对称美,增强应用意识和实践能力,提升学习兴趣,促进目标(3)的达成.
教学过程呈现
设计说明
观察、操作、体验,归纳特征,抽象概念.
问题驱动
发展素养
整体构建
类比探究
抽象概念
抽象能力、几何直观、推理能力.
学为中心,问题驱动,设计活动,体验过程.
整体构建,形成几何变化知识体系.
类比平移,用运动变化观点探究性质.
感受轴对称的数学价值和美学价值
教法
学法
思路
理念
目标
谢谢倾听
