人教版八年级上册 第十三章 等腰三角形专题 课件(共20张PPT)
文档属性
| 名称 | 人教版八年级上册 第十三章 等腰三角形专题 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 482.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-26 13:55:24 | ||
图片预览

文档简介
(共20张PPT)
育人 . 寻梦
专题二 等腰三角形
八年级数学
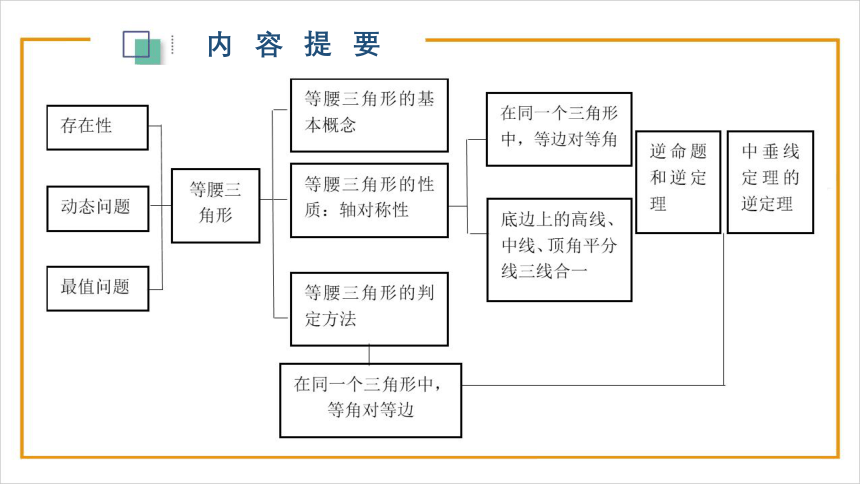
内容提要
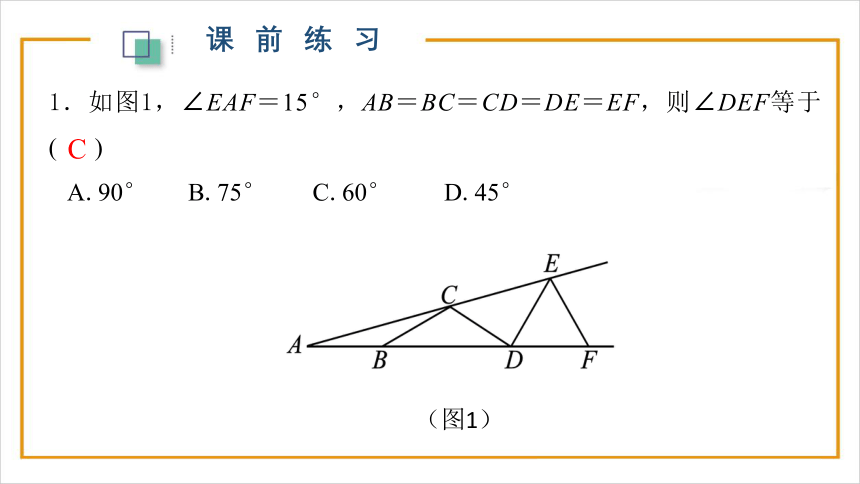
1.如图1,∠EAF=15°,AB=BC=CD=DE=EF,则∠DEF等于( )
A.90° B.75° C.60° D.45°
课前练习
(图1)
C
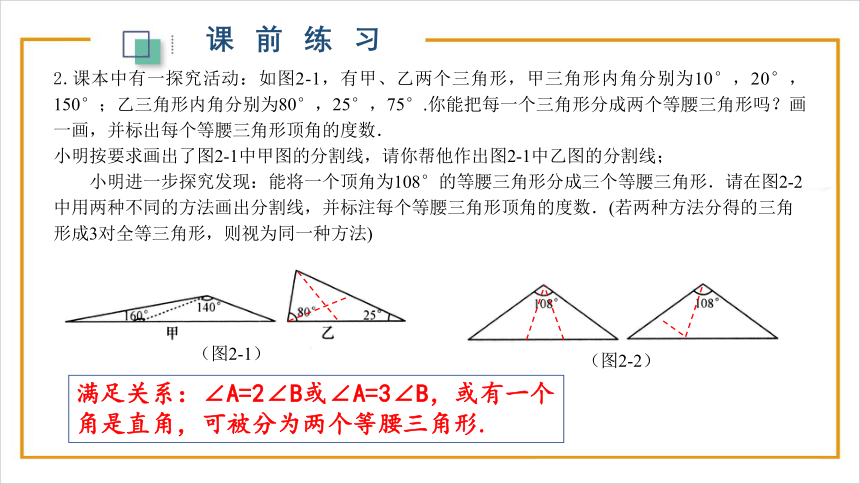
2.课本中有一探究活动:如图2-1,有甲、乙两个三角形,甲三角形内角分别为10°,20°,150°;乙三角形内角分别为80°,25°,75°.你能把每一个三角形分成两个等腰三角形吗?画一画,并标出每个等腰三角形顶角的度数.
小明按要求画出了图2-1中甲图的分割线,请你帮他作出图2-1中乙图的分割线;
小明进一步探究发现:能将一个顶角为108°的等腰三角形分成三个等腰三角形.请在图2-2中用两种不同的方法画出分割线,并标注每个等腰三角形顶角的度数.(若两种方法分得的三角形成3对全等三角形,则视为同一种方法)
课前练习
(图2-1)
(图2-2)
满足关系:∠A=2∠B或∠A=3∠B,或有一个角是直角,可被分为两个等腰三角形.
例题精析
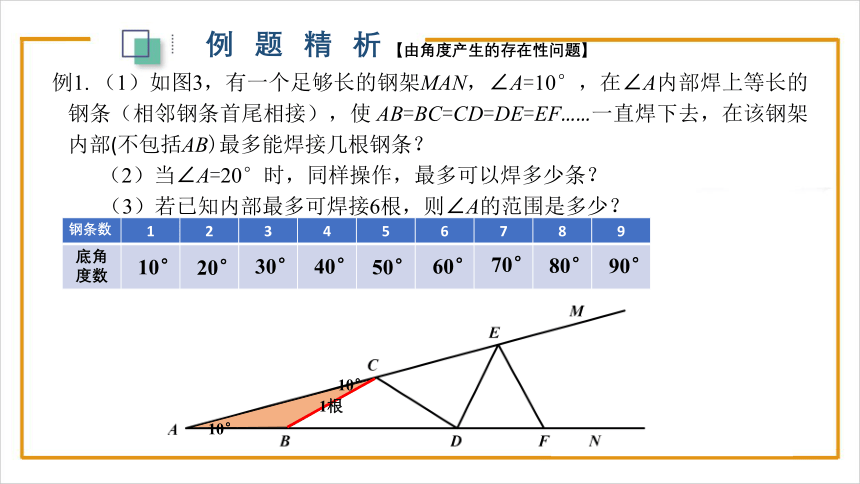
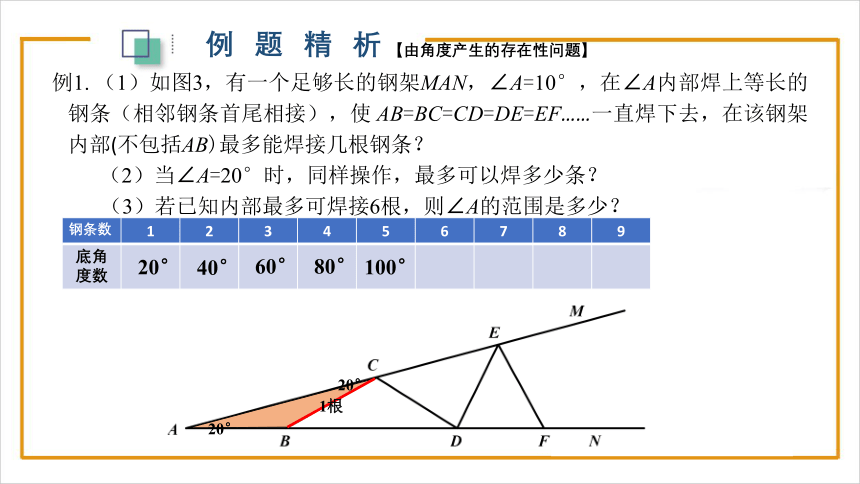
例1. (1)如图3,有一个足够长的钢架MAN,∠A=10°,在∠A内部焊上等长的钢条(相邻钢条首尾相接),使 AB=BC=CD=DE=EF……一直焊下去,在该钢架内部(不包括AB)最多能焊接几根钢条?
(2)当∠A=20°时,同样操作,最多可以焊多少条?
(3)若已知内部最多可焊接6根,则∠A的范围是多少?
【由角度产生的存在性问题】
钢条数 1 2 3 4 5 6 7 8 9
底角度数
1根
10°
10°
10°
20°
30°
40°
50°
60°
70°
80°
90°
例题精析
例1. (1)如图3,有一个足够长的钢架MAN,∠A=10°,在∠A内部焊上等长的钢条(相邻钢条首尾相接),使 AB=BC=CD=DE=EF……一直焊下去,在该钢架内部(不包括AB)最多能焊接几根钢条?
(2)当∠A=20°时,同样操作,最多可以焊多少条?
(3)若已知内部最多可焊接6根,则∠A的范围是多少?
【由角度产生的存在性问题】
钢条数 1 2 3 4 5 6 7 8 9
底角度数
1根
20°
20°
20°
40°
60°
80°
100°
例题精析
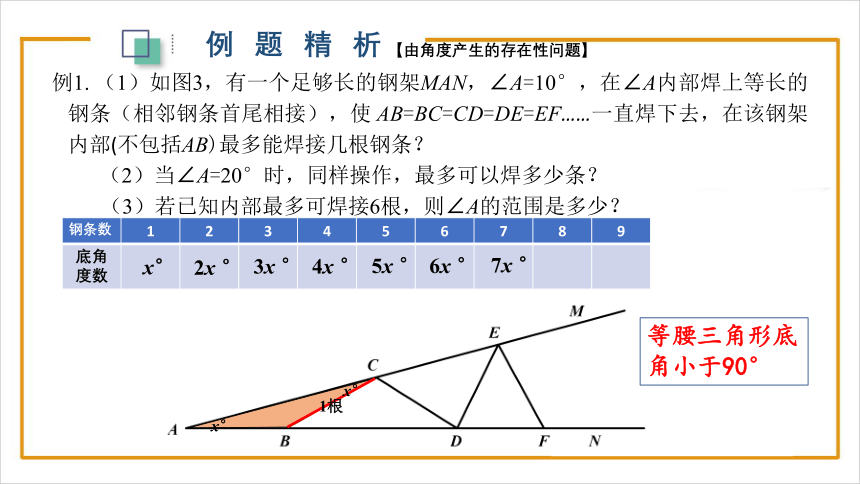
例1. (1)如图3,有一个足够长的钢架MAN,∠A=10°,在∠A内部焊上等长的钢条(相邻钢条首尾相接),使 AB=BC=CD=DE=EF……一直焊下去,在该钢架内部(不包括AB)最多能焊接几根钢条?
(2)当∠A=20°时,同样操作,最多可以焊多少条?
(3)若已知内部最多可焊接6根,则∠A的范围是多少?
【由角度产生的存在性问题】
钢条数 1 2 3 4 5 6 7 8 9
底角度数
1根
x°
x°
x°
2x °
3x °
4x °
5x °
6x °
7x °
等腰三角形底角小于90°
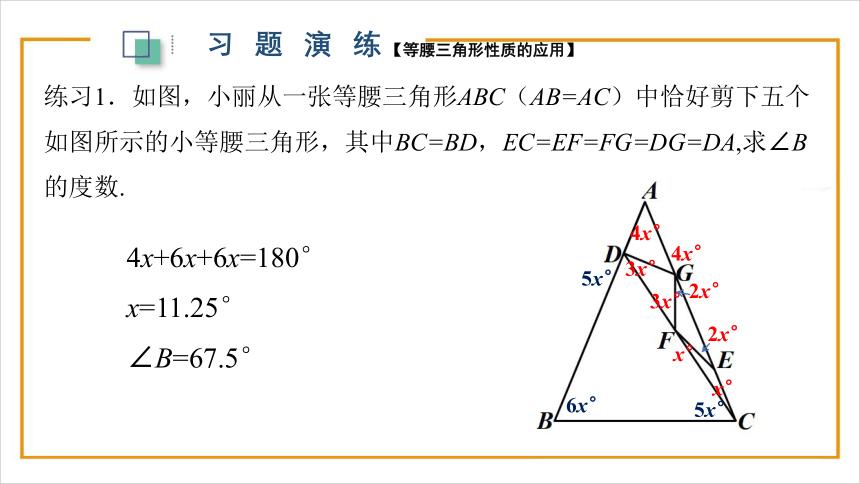
练习1.如图,小丽从一张等腰三角形ABC(AB=AC)中恰好剪下五个如图所示的小等腰三角形,其中BC=BD,EC=EF=FG=DG=DA,求∠B的度数.
习题演练
【等腰三角形性质的应用】
x°
3x°
3x°
4x°
x°
2x°
2x°
4x°
5x°
5x°
6x°
4x+6x+6x=180°
x=11.25°
∠B=67.5°
例题精析
【因底、腰产生的分类讨论】
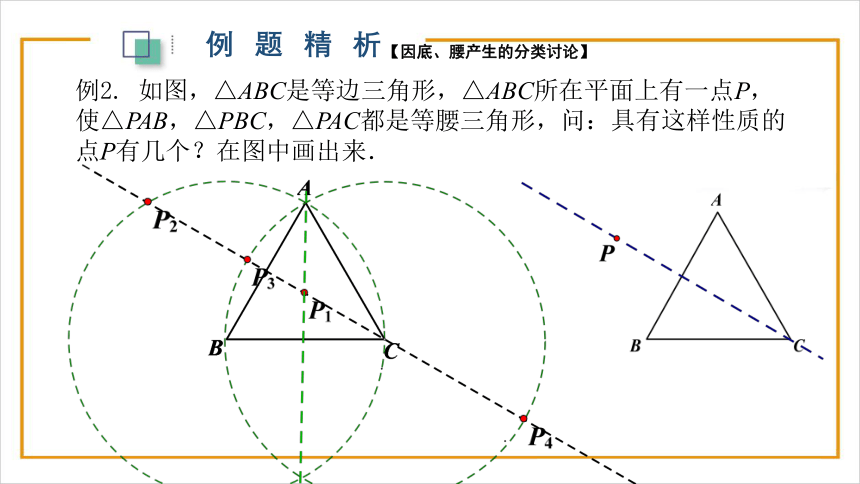
例2. 如图,△ABC是等边三角形,△ABC所在平面上有一点P,使△PAB,△PBC,△PAC都是等腰三角形,问:具有这样性质的点P有几个?在图中画出来.
例题精析
【因底、腰产生的分类讨论】
练习2.如图,在△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出不同的等腰三角形的个数最多为( )
A.4 B.5 C.6 D.7
习题演练
【因底、腰产生的分类讨论】
以AC为腰:△ACD1
以AC为底:△ACD2
以BC为腰:△BCD3,△BCD4,△BCD5
以BC为底:△BCD2
以AB为底:△ABD6
D
分类讨论:以已知边为腰或底进行分类.
练习2.如图,在△ABC中,∠ABC=70°,∠BAC=40°.P为直线CB上一动点,并沿直线CB向左移动,若点P与△ABC三个顶点中的至少两个顶点构造成等腰三角形,则将点P在直线CB上进行标记,那么满足条件的点P的位置有 ( )
A.4个 B.6个 C.8个 D.9个
习题演练
【因底、腰产生的分类讨论】
C
例3. 如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2㎝,设运动的时间为t秒.
求:t为何值时,△BCP为等腰三角形.
例题精析
【运动问题中的等腰三角形】
【运动问题中的等腰三角形】
习题演练
练习4.如图,∠AOB=60°,点C是BO延长线上的一点,OC=10cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P,Q同时出发,用t(s)表示移动的时间,当t为何值时,△POQ是等腰三角形?
点P在O左侧:∠POQ=120°
PO=OQ
点P在O右侧:∠POQ=60°,由△POQ是等腰三角形,可得△POQ是等边三角形.
PO=OQ
t
2t
10-2t=t
t=
2t-10=t
t=10
例4 . 如图,等腰三角形ABC的底边BC的长为6,面积为30,腰AB的垂直平分线EF分别交AB,AC于点E,F.若D为底边BC的中点,M为线段EF上一动点,则△BDM的周长的最小值为_______.
例题精析
【等腰三角形中的最值问题】
13
线段和最短问题应用轴对称性转移线段位置.
练习4.如图,在等腰△ABC中,AB=BC=5,AC=6,∠ABC的平分线交AC于点D,M、N分别是BD和BC上的动点,则CM+MN的最小值是_______.
习题演练
【等腰三角形中的最值问题】
课后练习
1.如图11,在4×4方格中,以AB为一边,第三个顶点也在格点上的等腰三角形可以作出( )
A.7个 B.6个
C.4个 D.3个
(图11)
A
课后练习
2.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B,C重合),连结AD,作∠ADE=40°,DE交线段AC于点E.在点D的运动过程中,当∠BDA度数是多少时,△ADE是等腰三角形.请直接写出∠BDA的度数_______________.
80°或110°
课后练习
3.如图,边长为4的正方形ABCD中,请画出以D为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3即可).
课后练习
3.如图,边长为4的正方形ABCD中,请画出以D为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形
(只要画出示意图,并在等腰三角形长为3的边上标注数字).
育人 . 寻梦
专题二 等腰三角形
八年级数学
内容提要
1.如图1,∠EAF=15°,AB=BC=CD=DE=EF,则∠DEF等于( )
A.90° B.75° C.60° D.45°
课前练习
(图1)
C
2.课本中有一探究活动:如图2-1,有甲、乙两个三角形,甲三角形内角分别为10°,20°,150°;乙三角形内角分别为80°,25°,75°.你能把每一个三角形分成两个等腰三角形吗?画一画,并标出每个等腰三角形顶角的度数.
小明按要求画出了图2-1中甲图的分割线,请你帮他作出图2-1中乙图的分割线;
小明进一步探究发现:能将一个顶角为108°的等腰三角形分成三个等腰三角形.请在图2-2中用两种不同的方法画出分割线,并标注每个等腰三角形顶角的度数.(若两种方法分得的三角形成3对全等三角形,则视为同一种方法)
课前练习
(图2-1)
(图2-2)
满足关系:∠A=2∠B或∠A=3∠B,或有一个角是直角,可被分为两个等腰三角形.
例题精析
例1. (1)如图3,有一个足够长的钢架MAN,∠A=10°,在∠A内部焊上等长的钢条(相邻钢条首尾相接),使 AB=BC=CD=DE=EF……一直焊下去,在该钢架内部(不包括AB)最多能焊接几根钢条?
(2)当∠A=20°时,同样操作,最多可以焊多少条?
(3)若已知内部最多可焊接6根,则∠A的范围是多少?
【由角度产生的存在性问题】
钢条数 1 2 3 4 5 6 7 8 9
底角度数
1根
10°
10°
10°
20°
30°
40°
50°
60°
70°
80°
90°
例题精析
例1. (1)如图3,有一个足够长的钢架MAN,∠A=10°,在∠A内部焊上等长的钢条(相邻钢条首尾相接),使 AB=BC=CD=DE=EF……一直焊下去,在该钢架内部(不包括AB)最多能焊接几根钢条?
(2)当∠A=20°时,同样操作,最多可以焊多少条?
(3)若已知内部最多可焊接6根,则∠A的范围是多少?
【由角度产生的存在性问题】
钢条数 1 2 3 4 5 6 7 8 9
底角度数
1根
20°
20°
20°
40°
60°
80°
100°
例题精析
例1. (1)如图3,有一个足够长的钢架MAN,∠A=10°,在∠A内部焊上等长的钢条(相邻钢条首尾相接),使 AB=BC=CD=DE=EF……一直焊下去,在该钢架内部(不包括AB)最多能焊接几根钢条?
(2)当∠A=20°时,同样操作,最多可以焊多少条?
(3)若已知内部最多可焊接6根,则∠A的范围是多少?
【由角度产生的存在性问题】
钢条数 1 2 3 4 5 6 7 8 9
底角度数
1根
x°
x°
x°
2x °
3x °
4x °
5x °
6x °
7x °
等腰三角形底角小于90°
练习1.如图,小丽从一张等腰三角形ABC(AB=AC)中恰好剪下五个如图所示的小等腰三角形,其中BC=BD,EC=EF=FG=DG=DA,求∠B的度数.
习题演练
【等腰三角形性质的应用】
x°
3x°
3x°
4x°
x°
2x°
2x°
4x°
5x°
5x°
6x°
4x+6x+6x=180°
x=11.25°
∠B=67.5°
例题精析
【因底、腰产生的分类讨论】
例2. 如图,△ABC是等边三角形,△ABC所在平面上有一点P,使△PAB,△PBC,△PAC都是等腰三角形,问:具有这样性质的点P有几个?在图中画出来.
例题精析
【因底、腰产生的分类讨论】
练习2.如图,在△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出不同的等腰三角形的个数最多为( )
A.4 B.5 C.6 D.7
习题演练
【因底、腰产生的分类讨论】
以AC为腰:△ACD1
以AC为底:△ACD2
以BC为腰:△BCD3,△BCD4,△BCD5
以BC为底:△BCD2
以AB为底:△ABD6
D
分类讨论:以已知边为腰或底进行分类.
练习2.如图,在△ABC中,∠ABC=70°,∠BAC=40°.P为直线CB上一动点,并沿直线CB向左移动,若点P与△ABC三个顶点中的至少两个顶点构造成等腰三角形,则将点P在直线CB上进行标记,那么满足条件的点P的位置有 ( )
A.4个 B.6个 C.8个 D.9个
习题演练
【因底、腰产生的分类讨论】
C
例3. 如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2㎝,设运动的时间为t秒.
求:t为何值时,△BCP为等腰三角形.
例题精析
【运动问题中的等腰三角形】
【运动问题中的等腰三角形】
习题演练
练习4.如图,∠AOB=60°,点C是BO延长线上的一点,OC=10cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P,Q同时出发,用t(s)表示移动的时间,当t为何值时,△POQ是等腰三角形?
点P在O左侧:∠POQ=120°
PO=OQ
点P在O右侧:∠POQ=60°,由△POQ是等腰三角形,可得△POQ是等边三角形.
PO=OQ
t
2t
10-2t=t
t=
2t-10=t
t=10
例4 . 如图,等腰三角形ABC的底边BC的长为6,面积为30,腰AB的垂直平分线EF分别交AB,AC于点E,F.若D为底边BC的中点,M为线段EF上一动点,则△BDM的周长的最小值为_______.
例题精析
【等腰三角形中的最值问题】
13
线段和最短问题应用轴对称性转移线段位置.
练习4.如图,在等腰△ABC中,AB=BC=5,AC=6,∠ABC的平分线交AC于点D,M、N分别是BD和BC上的动点,则CM+MN的最小值是_______.
习题演练
【等腰三角形中的最值问题】
课后练习
1.如图11,在4×4方格中,以AB为一边,第三个顶点也在格点上的等腰三角形可以作出( )
A.7个 B.6个
C.4个 D.3个
(图11)
A
课后练习
2.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B,C重合),连结AD,作∠ADE=40°,DE交线段AC于点E.在点D的运动过程中,当∠BDA度数是多少时,△ADE是等腰三角形.请直接写出∠BDA的度数_______________.
80°或110°
课后练习
3.如图,边长为4的正方形ABCD中,请画出以D为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3即可).
课后练习
3.如图,边长为4的正方形ABCD中,请画出以D为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形
(只要画出示意图,并在等腰三角形长为3的边上标注数字).
