山西省晋中市榆次第一中学校2024-2025学年高二上学期开学考试(暑假作业检查)数学试题(PDF版,无答案)
文档属性
| 名称 | 山西省晋中市榆次第一中学校2024-2025学年高二上学期开学考试(暑假作业检查)数学试题(PDF版,无答案) |

|
|
| 格式 | |||
| 文件大小 | 540.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-26 00:00:00 | ||
图片预览

文档简介
高二年级暑假学业检查数学
时间:90 分钟 满分:150 分
一、选择题(本大题共 8 个小题,每小题 5 分,共 40 分.在每小题给出的四个
选项中,只有一项是符合题意的.)
1.设 z= +2i,则|z|=( )
A.0 B. C.1 D.
2.若{a,b,c}构成空间的一个基底,则下列向量不共面的是( )
A b+c,b,b-c B a,a+b,a-b
C a+b,a-b,c D a+b,a+b+c,c
3. ABC 的内角 A, B,C 的对边分别为a,b,c ,且 (2b c)cos A = a cosC,b = 2 3 ,若边
BC 的中线等于 3,则 ABC 的面积为( )
9 3 3 3
A 9 3 B C 3 3 D
2 2
4.河南博物院主展馆的主体建筑以元代登封古观星台为原型,经艺术夸张演绎成“戴冠的
金字塔”造型,冠部为“方斗”形,上扬下覆,取上承“甘露”、下纳“地气”之意.冠部以及冠
部下方均可视为正四棱台.已知一个“方斗”的上底面与下底面的面积之比为1: 4,高为 2,
56
体积为 ,则该“方斗”的侧面积为( )
3
A.24 B.12 C.24 5 D.12 5
5.设 O为正方形 ABCD的中心,在 O,A,B,C,D中任取 3 点,则取到的 3 点共线的概率
为( )
1 2 1 4
A. B. C. D.
5 5 2 5
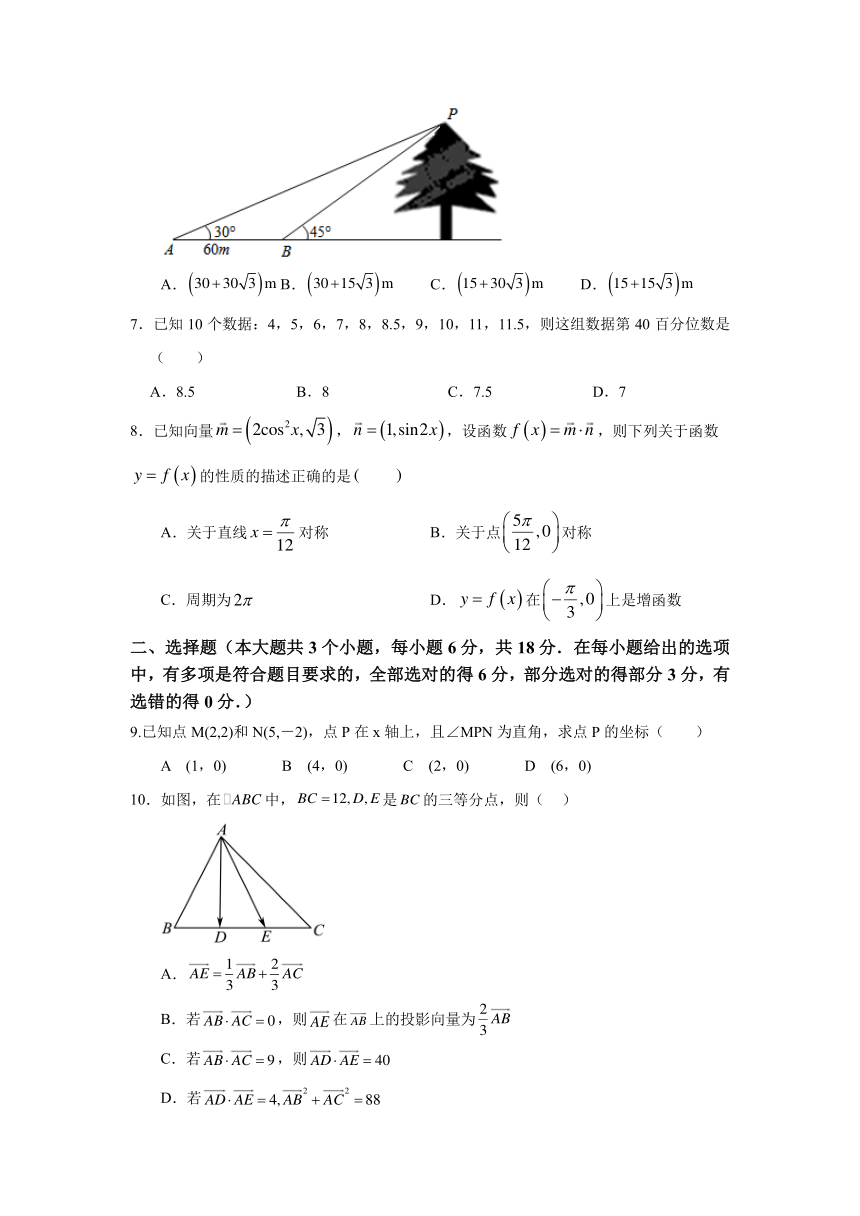
6.如图所示,为测一树的高度,在地面上选取A 、 B 两点,从A 、 B 两点分别测得树尖的
仰角为30 、45 ,且A 、 B 两点之间的距离为60m,则树的高度为( )
{#{QQABDBQQEk5ogICQgkAJSJBAACAJB5qgEC0EGwKHC6QCAmKQQsIkEAiLEeCgCEaQgQGChANAqAMwoCAAAYQNIAFNIAA=B}A#}A=}#}
A. (30+ 30 3)m B. (30+15 3 )m C. (15+ 30 3)m D. (15+15 3)m
7.已知 10 个数据:4,5,6,7,8,8.5,9,10,11,11.5,则这组数据第 40 百分位数是
( )
A.8.5 B.8 C.7.5 D.7
m = (2cos28.已知向量 x, 3), n = (1,sin2x),设函数 f (x) = m n ,则下列关于函数
y = f (x)的性质的描述正确的是 ( )
5
A.关于直线 x = 对称 B.关于点 ,0 对称
12 12
C.周期为2 D. y = f (x)在 ,0 上是增函数
3
二、选择题(本大题共 3 个小题,每小题 6 分,共 18 分.在每小题给出的选项
中,有多项是符合题目要求的,全部选对的得 6 分,部分选对的得部分 3 分,有
选错的得 0 分.)
9.已知点 M(2,2)和 N(5,-2),点 P 在 x 轴上,且∠MPN 为直角,求点 P 的坐标( )
A (1,0) B (4,0) C (2,0) D (6,0)
10.如图,在 ABC 中,BC =12, D, E是 BC 的三等分点,则( )
1 2
A. AE = AB + AC
3 3
2
B.若 AB AC = 0,则 AE 在 AB 上的投影向量为 AB
3
C.若 AB AC = 9,则 AD AE = 40
2 2
D.若 AD AE = 4, AB + AC = 88
{#{QQABDBQQEk5ogICQgkAJSJBAACAJB5qgEC0EGwKHC6QCAmKQQsIkEAiLEeCgCEaQgQGChANAqAMwoCAAAYQNIAFNIAA=B}A#}A=}#}
11.如图,在四棱锥 P﹣ABCD 中,PA⊥平面 ABCD,底面 ABCD 是正方形,且 PA=AB=
2,E,F分别为 PD,PB的中点,则( )
A.EF⊥平面 PAC
B.四棱锥 P﹣ABCD的外接球的表面积为 48π
C.CF与平面 ABCD所成角的正弦值为
D.点 A到平面 EFC的距离为
三、填空题(本大题共 3 个小题,每小题 5 分,共 15 分.)
12.经过 A(0,2),B(-1,0)两点的直线的方向向量为(1,k),求 k 的值为________.
13.过A(m +2,m -3),B(3-m-m ,2m)两点的直线 l的倾斜角为45°,求m的值为________.
14.如图,若斜边长为2 2 的等腰直角 A B C ( B 与O 重合)是水平放置的 ABC 的直
观图,则 ABC 的面积为________.
四、解答题(本大题共 5 个小题,共 77 分.解答应写出文字说明、证明过程或
演算步骤.)
15.(13 分)利用空间向量知识完成本题.
(1)如图 15-1, 在长方体 ABCD-A1B1C1D1中 AB=4, BC=3, CC1=2. 线段 B1C 上是否存
在点 P, 使得 A1P 平行于平面 ACD1?
(2)如图 15-2, 在平行六面体 ABCD-A1B1C1D1中 AB=AD=AA1=1,∠A1AB=∠A1AD=
∠BAD=60°, 求证直线 A1C 垂直于平面 BDD1B1。
(3)如图 15-3, 在棱长为 1 的正方体中, E 为线段 A1B1 的中点, F 为线段 AB 的中点.
{#{QQABDBQQEk5ogICQgkAJSJBAACAJB5qgEC0EGwKHC6QCmAKQQsIkEAiLEeCgCEaQgQGChANAqAMwoCAAAYQNIAFNIAA=B}A#}A=}#}
i 求点 B 到直线 AC1 的距离;
ii 求直线 FC 到平面 A1C1的距离.
图 15-1 图 15-2 图 15-3
16.(15 分)判断下列各对直线是否平行或垂直:
(1)经过 A(2,3),B(-1,0)两点的直线 l ,与经过 P(1,0)且斜率为 1 的直线 l ;
(2)经过 C(3,1),D(-2,0)两点的直线 l ,与经过点 M(1,-4)且斜率为-5 的直线 l .
(3)试确定 m 的值,使过 A(m,1),B(-1,m)两点的直线与过 P(1,2),Q(-5,0)两点
的直线:I 平行;II 垂直.
17.(15 分)在△ABC中,角 A、B、C所对的边分别为 a、b、c,且 .
(1)求 的值;
(2)若 ,求 bc的最大值.
18.(17 分)甲、乙二人用 4 张扑克牌(分别是红桃 2,红桃 3,红桃 4,方片 4)玩游戏,他们
将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(1)写出甲、乙抽到牌的所有情况;
(2)若甲抽到红桃 3,则乙抽到的牌的数字比 3 大的概率是多少?
(3)甲、乙约定,若甲抽到的牌的数字比乙的大,则甲胜;否则乙胜,你认为此游戏
是否公平?为什么?
19.(17 分)如图在三棱锥 A﹣BCD中,平面 ABD⊥平面 BCD,AB=AD,O为 BD的中点.
(1)证明:OA⊥CD;
(2)若△OCD是边长为 1 的等边三角形,点 E在棱 AD上,DE=2EA,且二面角 E﹣
BC﹣D的大小为 45°,求三棱锥 A﹣BCD的体积.
{#{QQABDBQQEk5ogICQgkAJSJBAACAJB5qgEC0EGwKHC6QCmAKQQsIkEAiLEeCgCEaQgQGChANAqAMwoCAAAYQNIAFNIAA=B}A#}A=}#}
时间:90 分钟 满分:150 分
一、选择题(本大题共 8 个小题,每小题 5 分,共 40 分.在每小题给出的四个
选项中,只有一项是符合题意的.)
1.设 z= +2i,则|z|=( )
A.0 B. C.1 D.
2.若{a,b,c}构成空间的一个基底,则下列向量不共面的是( )
A b+c,b,b-c B a,a+b,a-b
C a+b,a-b,c D a+b,a+b+c,c
3. ABC 的内角 A, B,C 的对边分别为a,b,c ,且 (2b c)cos A = a cosC,b = 2 3 ,若边
BC 的中线等于 3,则 ABC 的面积为( )
9 3 3 3
A 9 3 B C 3 3 D
2 2
4.河南博物院主展馆的主体建筑以元代登封古观星台为原型,经艺术夸张演绎成“戴冠的
金字塔”造型,冠部为“方斗”形,上扬下覆,取上承“甘露”、下纳“地气”之意.冠部以及冠
部下方均可视为正四棱台.已知一个“方斗”的上底面与下底面的面积之比为1: 4,高为 2,
56
体积为 ,则该“方斗”的侧面积为( )
3
A.24 B.12 C.24 5 D.12 5
5.设 O为正方形 ABCD的中心,在 O,A,B,C,D中任取 3 点,则取到的 3 点共线的概率
为( )
1 2 1 4
A. B. C. D.
5 5 2 5
6.如图所示,为测一树的高度,在地面上选取A 、 B 两点,从A 、 B 两点分别测得树尖的
仰角为30 、45 ,且A 、 B 两点之间的距离为60m,则树的高度为( )
{#{QQABDBQQEk5ogICQgkAJSJBAACAJB5qgEC0EGwKHC6QCAmKQQsIkEAiLEeCgCEaQgQGChANAqAMwoCAAAYQNIAFNIAA=B}A#}A=}#}
A. (30+ 30 3)m B. (30+15 3 )m C. (15+ 30 3)m D. (15+15 3)m
7.已知 10 个数据:4,5,6,7,8,8.5,9,10,11,11.5,则这组数据第 40 百分位数是
( )
A.8.5 B.8 C.7.5 D.7
m = (2cos28.已知向量 x, 3), n = (1,sin2x),设函数 f (x) = m n ,则下列关于函数
y = f (x)的性质的描述正确的是 ( )
5
A.关于直线 x = 对称 B.关于点 ,0 对称
12 12
C.周期为2 D. y = f (x)在 ,0 上是增函数
3
二、选择题(本大题共 3 个小题,每小题 6 分,共 18 分.在每小题给出的选项
中,有多项是符合题目要求的,全部选对的得 6 分,部分选对的得部分 3 分,有
选错的得 0 分.)
9.已知点 M(2,2)和 N(5,-2),点 P 在 x 轴上,且∠MPN 为直角,求点 P 的坐标( )
A (1,0) B (4,0) C (2,0) D (6,0)
10.如图,在 ABC 中,BC =12, D, E是 BC 的三等分点,则( )
1 2
A. AE = AB + AC
3 3
2
B.若 AB AC = 0,则 AE 在 AB 上的投影向量为 AB
3
C.若 AB AC = 9,则 AD AE = 40
2 2
D.若 AD AE = 4, AB + AC = 88
{#{QQABDBQQEk5ogICQgkAJSJBAACAJB5qgEC0EGwKHC6QCAmKQQsIkEAiLEeCgCEaQgQGChANAqAMwoCAAAYQNIAFNIAA=B}A#}A=}#}
11.如图,在四棱锥 P﹣ABCD 中,PA⊥平面 ABCD,底面 ABCD 是正方形,且 PA=AB=
2,E,F分别为 PD,PB的中点,则( )
A.EF⊥平面 PAC
B.四棱锥 P﹣ABCD的外接球的表面积为 48π
C.CF与平面 ABCD所成角的正弦值为
D.点 A到平面 EFC的距离为
三、填空题(本大题共 3 个小题,每小题 5 分,共 15 分.)
12.经过 A(0,2),B(-1,0)两点的直线的方向向量为(1,k),求 k 的值为________.
13.过A(m +2,m -3),B(3-m-m ,2m)两点的直线 l的倾斜角为45°,求m的值为________.
14.如图,若斜边长为2 2 的等腰直角 A B C ( B 与O 重合)是水平放置的 ABC 的直
观图,则 ABC 的面积为________.
四、解答题(本大题共 5 个小题,共 77 分.解答应写出文字说明、证明过程或
演算步骤.)
15.(13 分)利用空间向量知识完成本题.
(1)如图 15-1, 在长方体 ABCD-A1B1C1D1中 AB=4, BC=3, CC1=2. 线段 B1C 上是否存
在点 P, 使得 A1P 平行于平面 ACD1?
(2)如图 15-2, 在平行六面体 ABCD-A1B1C1D1中 AB=AD=AA1=1,∠A1AB=∠A1AD=
∠BAD=60°, 求证直线 A1C 垂直于平面 BDD1B1。
(3)如图 15-3, 在棱长为 1 的正方体中, E 为线段 A1B1 的中点, F 为线段 AB 的中点.
{#{QQABDBQQEk5ogICQgkAJSJBAACAJB5qgEC0EGwKHC6QCmAKQQsIkEAiLEeCgCEaQgQGChANAqAMwoCAAAYQNIAFNIAA=B}A#}A=}#}
i 求点 B 到直线 AC1 的距离;
ii 求直线 FC 到平面 A1C1的距离.
图 15-1 图 15-2 图 15-3
16.(15 分)判断下列各对直线是否平行或垂直:
(1)经过 A(2,3),B(-1,0)两点的直线 l ,与经过 P(1,0)且斜率为 1 的直线 l ;
(2)经过 C(3,1),D(-2,0)两点的直线 l ,与经过点 M(1,-4)且斜率为-5 的直线 l .
(3)试确定 m 的值,使过 A(m,1),B(-1,m)两点的直线与过 P(1,2),Q(-5,0)两点
的直线:I 平行;II 垂直.
17.(15 分)在△ABC中,角 A、B、C所对的边分别为 a、b、c,且 .
(1)求 的值;
(2)若 ,求 bc的最大值.
18.(17 分)甲、乙二人用 4 张扑克牌(分别是红桃 2,红桃 3,红桃 4,方片 4)玩游戏,他们
将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(1)写出甲、乙抽到牌的所有情况;
(2)若甲抽到红桃 3,则乙抽到的牌的数字比 3 大的概率是多少?
(3)甲、乙约定,若甲抽到的牌的数字比乙的大,则甲胜;否则乙胜,你认为此游戏
是否公平?为什么?
19.(17 分)如图在三棱锥 A﹣BCD中,平面 ABD⊥平面 BCD,AB=AD,O为 BD的中点.
(1)证明:OA⊥CD;
(2)若△OCD是边长为 1 的等边三角形,点 E在棱 AD上,DE=2EA,且二面角 E﹣
BC﹣D的大小为 45°,求三棱锥 A﹣BCD的体积.
{#{QQABDBQQEk5ogICQgkAJSJBAACAJB5qgEC0EGwKHC6QCmAKQQsIkEAiLEeCgCEaQgQGChANAqAMwoCAAAYQNIAFNIAA=B}A#}A=}#}
同课章节目录
