5.3.1样本空间与事件(教学课件)——高中数学人教B版(2019)必修第二册(共40张PPT)
文档属性
| 名称 | 5.3.1样本空间与事件(教学课件)——高中数学人教B版(2019)必修第二册(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-26 00:00:00 | ||
图片预览











文档简介
(共40张PPT)
人教B版(2019)必修第二册
5.3.1样本空间与事件
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
了解必然现象和随机现象,了解不可能事件、必然事件及随机事件
01
理解事件与基本事件的定义,会求试验中的基本事件空间以及事件A包含的基本事件的个数
02
明确随机事件发生的概率,并能直观判断两个事件概率的大小,培养学生的逻辑推理能力
03
探索新知
part 02
探索新知
02
实例分析
如果要你将以下日常生活中的现象进行分类,你会依据什么来分?分类的结果是怎样的?
知识点1 随机现象
(1)某人练习投篮5次,结果投中了3次;
(2)每天早晨太阳都从东边升起;
(3)某人一个小时内接到10个电话;
(4)将一石块抛向空中,石块掉落下来;
(5)走到一个红绿灯路口时,前方正好是绿灯;
(6)实心铁球丢进水里,铁球会沉到水底;
(7)买一张福利彩票,没中奖.
不确定
确定
不确定
确定
不确定
确定
不确定
探索新知
02
抽象概括
请你按照上述现象的类别,分别给两类现象起个名字.
随机现象:一定条件下,发生的结果事先不能确定的现象就是随机现象(或偶然现象).
也就是说,对于随机现象而言,如果在同一条件下进行多次观察,每次观察的结果不一定相同,事先很难确定哪种结果会出现.
知识点1 随机现象
必然现象:一定条件下,发生的结果事先能确定的现象就是必然现象(或确定性现象).
探索新知
02
抽象概括
你能举出身边熟悉的随机现象和必然现象的例子吗?
知识点1 随机现象
(1)抛一枚硬币,出现正面;
(2)掷一个骰子,出现的点数为6;
(3)新生婴儿的性别为女.
(4)某地区10月份的平均气温比另一地区高;
(5)某公共汽车站某时刻的等车人数为6;
(6)从一批产品中,依次任选3件,其中恰有一等品2件;
(7)从一批灯泡中任取一只,其寿命大于10000h;
(8)电荷同性相斥,异性相吸;
(9)任意实数x,都有x≥0;
(10)明天本地下雨.
随机现象
随机现象
随机现象
随机现象
随机现象
随机现象
随机现象
必然现象
随机现象
随机现象
探索新知
02
实例分析
知识点2 样本点和样本空间
大千世界充满了随机现象,
偶然现象蕴含着必然的规律.
随机现象
生活现象
观察
实验
概念一
比如:抛一枚硬币,究竟会出现正面向上还是反面向上呢?我们可以做实验,观察.
探索新知
02
实例分析
知识点2 样本点和样本空间
随机试验:在相同的条件下,对随机现象所进行的观察或实验称为随机试验(简称为试验)
随机现象
生活现象
随机试验
观察
实验
概念二
比如:抛一枚硬币,掷一个均匀的骰子等
探索新知
02
实例分析
知识点2 样本点和样本空间
随机现象
生活现象
随机试验
观察
实验
概念二
三个
条件
条 件
过 程
结 果
(1)可重复性:试验可以在相同条件下重复进行;
(2)随机性:不能预知每次试验的具体结果;
(3)确定性:试验的所有可能结果是明确可知的.
说明:对于随机试验而言,每次试验的结果如何,是无法预料的,但随着试验的重复进行,其结果的出现会呈现出一定的规律性.
探索新知
02
实例分析
知识点2 样本点和样本空间
随机现象
生活现象
随机试验
观察
实验
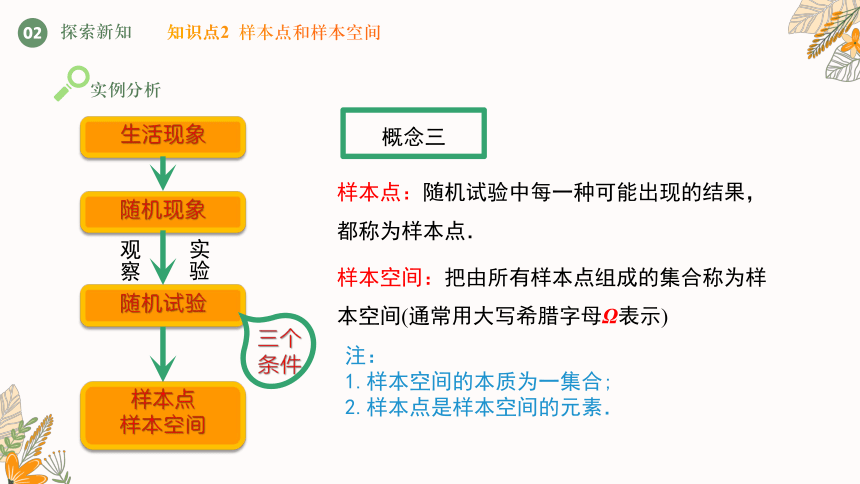
概念三
样本点
样本空间
三个
条件
样本点:随机试验中每一种可能出现的结果,都称为样本点.
样本空间:把由所有样本点组成的集合称为样本空间(通常用大写希腊字母Ω表示)
注:
1.样本空间的本质为一集合;
2.样本点是样本空间的元素.
探索新知
02
实例分析
请你分别指出试验:抛掷一枚硬币、掷一个骰子的样本点和样本空间.
知识点2 样本点和样本空间
(1)抛一枚硬币,如果样本点记为“正面向上”、“反面向上”,则样本空间为Ω={正面向上,反面向上}.
思考:样本点可以用更简单的方式表示吗?
如果把样本点“正面向上”、“反面向上”分别记为“1”、“0”,
则样本空间为Ω={1,0}.
(2)掷一个骰子,如果样本点用朝上的面的点数表示,则其样本空间为Ω={1,2,3,4,5,6}
探索新知
02
例1 先后抛出两枚硬币,观察正反面出现的情况,选择合适的方法表示样本点,并写出样本空间.
表示1:
用Z表示“正面朝上”;用F表示“反面朝上”.
表示2:
用1表示“正面朝上”;用0表示“反面朝上”.
表示3:
注:1.样本空间的表示需要选择简洁的方式;
2.无论是哪种符号,都要先说明符号表示的意思.
知识点2 样本点和样本空间
探索新知
02
追问:连续抛掷一枚骰子2次,观察朝上的面的点数,写出对应的样本空间;
解:对于试验,用表示抛掷的结果,其中表示第一次掷出的点数,表示第二次掷出的点数,则所有可能的结果如下表.
于是,试验共有个样本点.因此,该试验的样本空间为
这里的和是不同的样本点,分别表示连续抛掷一枚子2次,“第一次掷出的点数为1,第二次掷出的点数为 2”和“第一次掷出的点数为 2,第二次掷出的点数1”.
知识点2 样本点和样本空间
探索新知
02
追问:连续抛掷一枚骰子2次,观察朝上的面的点数,写出对应的样本空间;
解:对于试验,用表示抛掷的结果,其中表示第一次掷出的点数,表示第二次掷出的点数,则所有可能的结果如下表.
于是,试验共有个样本点.因此,该试验的样本空间为
注:从集合角度看,样本空间的表示可以有列举法和描述法,需要根据题目特点选择更为简洁的表示方法.
探索新知
02
实例分析
知识点3 随机事件
如果随机试验的样本空间为Ω,则随机事件A是Ω的一个非空真子集.
若试验的结果是A中的元素,则称A发生(或出现);否则,称A不发生(或不出现).
随机事件也可用自然语言描述.
探索新知
02
实例分析
掷一个骰子,观察朝上的面的点数,则样本空间Ω={1,2,3,4,5,6}.
思考:(1)事件A=“出现的点数为奇数”如何用集合语言来描述?如何用维恩图直观描述?
(1)事件A=“出现的点数为奇数”用集合语言表示为A={1,3,5},A是一个随机事件.
用韦恩图来直观地表示事件,如右图:
Ω
A
知识点3 随机事件
探索新知
02
实例分析
掷一个骰子,观察朝上的面的点数,则样本空间Ω={1,2,3,4,5,6}.
思考:(2)同学们分成小组,举例写出一些随机事件,用集合语言和自然语言两种方式来描述.
(2)B={2,4,6},B表示随机事件“出现的点数为偶数”.
如果掷骰子得到的点数为3,则可知上述随机事件A发生且随机事件B不发生.
知识点3 随机事件
探索新知
02
抽象概括
必然事件:任何一次随机试验的结果,一定是样本空间Ω中的元素,因此,可以认为每次实验中Ω一定发生,从而称Ω为必然事件.
知识点3 随机事件
不可能事件:因为空集不包含任何样本点,因此可以认为每次试验中一定不发生,从而称不可能事件.
事件:一般地,不可能事件、随机事件、必然事件都可简称为事件,通常用大写英文字母A,B,C,···来表示事件.因为事件一定是样本空间的子集,从而可以用表示集合的韦恩图来直观地表示事件,如图.
特别地,只含有一个样本点的事件称为基本事件.
Ω
A
探索新知
02
思考交流
对基本事件的理解
(2)基本事件的概念可类比集合中元素的概念,试验可能发生的全部结果是一个集合,其元素是基本事件,基本事件不能分解,不能同时发生(相当于集合中元素的互异性)
知识点3 随机事件
(1)基本事件具有如下性质:①不能再分解的最简单的随机事件;②不同的基本事件不可能同时发生.
(3)事件与基本事件的区别:基本事件是试验中不能再分解的最简单的随机事件,而事件可以由若干个基本事件组成.
探索新知
02
例2 张华练习投篮10次,观察张华投篮命中的次数,写出对应的样本空间,并用集合表示出事件A:投篮命中的次数不少于7次.
样本空间为Ω={0,1,2,3,4,5,6,7,8,9,10}
所要表示的事件为A={7,8,9,10}
知识点3 随机事件
例3 从含有3件次品的100件产品中任取5件,观察其中次品数,写出对应的样本空间,并说明事件A={0}的实际意义.
样本空间为Ω={0,1,2,3}
事件A={0}表示的实际意义是:抽取的5件产品中,没有次品
探索新知
02
抽象概括
知识点4 随机事件发生的概念
我们已经知道,事件发生的可能性大小可以用该事件发生的概率(也简称为事件的概率)来衡量,概率越大,代表越有可能发生.事件A发生的概率通常用P(A)表示.
在例3中,事件B ={4}是不可能事件,即B=,
我们将不可能事件发生的概率规定为0,将必然事件发生的概率规定为1,即
P()=0,P(Ω)=1
你认为任意事件发生的概率应该满足什么条件?说明理由.
对于任意事件A来说,显然应该有P(Φ)≤P(A)≤P(Ω),
因此P(A)应该满足不等式0≤P(A)≤1.
探索新知
02
例4 先后两次掷一个均匀的骰子,观察朝上的面的点数.
(1)写出对应的样本空间;
(2)用集合表示事件A:点数之和为3,事件B:点数之和不超过3;
(3)从直观上判断P(A)和P(B)的大小(指出P(A)≥P(B)或P(A)≤P(B)即可).
(1)用(1,2)表示第一次掷出1点,第二次掷出2点,其他的样本点用类似的方法表示,则可知所有样本点均可表示成(i,j)的形式,其中i,j都是1,2,3,4,5,6中的数.因此,样本空间Ω={(i,j)|1≤i≤6,1≤j≤6,i∈N,j∈N}
也可简写为Ω={(i,j)|i,j=1,2,3,4,5,6}
知识点4 随机事件发生的概念
(2)A={(1,2),(2,1)},B={(1,1),(1,2),(2,1)}
(3)P(A)≤P(B)
题型突破
part 03
题型突破
03
题型1 样本点与样本空间
例1 同时转动如图所示的两个转盘,记转盘甲得到的数为x,转盘乙得到的数为y,结果记为(x,y).
①写出这个试验的样本空间;
②求这个试验的样本点的总数;
③“x+y=5”这一事件包含哪几个样本点
“x<3,且y>1”呢
④“xy=4”这一事件包含哪几个样本点 “x=y”呢
分析解答本题要根据日常生活的经验,逐个列出所要求的结果.
解:①Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),
(4,2),(4,3),(4,4)}.
②样本点的总数为16.
③“x+y=5”包含以下4个样本点:(1,4),(2,3),(3,2),(4,1).
“x<3,且y>1”包含以下6个样本点:(1,2),(1,3),(1,4),(2,2),(2,3),(2,4).
④“xy=4”包含以下3个样本点:(1,4),(2,2),(4,1).
“x=y”包含以下4个样本点:(1,1),(2,2),(3,3),(4,4).
题型突破
03
解题通法
随机事件的结果是相对于条件而言的,要确定样本空间,
(1)必须明确事件发生的条件;
(2)根据题意,按一定的次序列出所有样本点.
特别要注意结果出现的机会是均等的,按规律去写,要做到既不重复也不遗漏.
题型1 样本点与样本空间
题型突破
03
题型1 样本点与样本空间
延伸探究 1:将例1中条件不变,改为求“x+y是偶数”这一事件包含哪些样本点
解: “x+y是偶数”包括两种情况:①x,y都是奇数;②x,y都是偶数,故“x+y是偶数”这一事件包含以下8个样本点:(1,1),(1,3),(3,1),(3,3),(2,2),(2,4),(4,2),(4,4).
延伸探究 2:在例1的条件下,“xy是偶数”这一事件是必然事件吗
解:当x,y均是奇数时,xy是奇数;当x,y中至少有一个是偶数时,xy是偶数,故“xy是偶数”这一事件是随机事件,而不是必然事件.
题型突破
03
题型2 事件类型的判断
例2判断下列事件哪些是必然事件,哪些是不可能事件,哪些是随机事件.
(1)“在地球上抛一石块,下落”;
(2)“在标准大气压下,温度低于0 ℃时,冰融化”;
(3)“某人射击一次,中靶”;
(4)“如果a>b,那么a-b>0”;
(5)“掷一枚硬币,出现正面”;
(6)“导体通电后,发热”;
(7)“从分别标有号数1,2,3,4,5的5张标签中任取一张,得到4号签”;
(8)“某电话机在1分钟内收到2次呼叫”;
(9)“没有水分,种子能发芽”;
(10)“在常温下,焊锡熔化”.
分析:根据在一定条件下必然事件必然发生,不可能事件不可能发生,随机事件可能发生也可能不发生判断.
解:事件(1)(4)(6)是必然事件;事件(2)(9)(10)是不可能事件;事件(3)(5)(7)(8)是随机事件.
题型突破
03
解题通法
事件类型的判断方法
要判定某事件是何种事件,首先要看清条件,因为三种事件都是相对于一定条件而言的.其次再看它是一定发生,是不一定发生,还是一定不发生.一定发生的是必然事件,不一定发生的是随机事件,一定不发生的是不可能事件.
题型2 事件类型的判断
题型突破
03
题型3 随机事件的概率
例3袋子中装有除颜色外其他均相同的编号为a,b的2个黑球和编号为c,d,e的3个红球,从中任意摸出2个球.
(1)写出该试验的样本空间;
(2)用集合表示事件A:恰好摸出1个黑球和1个红球;事件B:至少摸出1个黑球;
(3)从直观上判断P(A)和P(B)的大小.
分析:(1)可以利用树形图写出;(2)找出恰好摸出1个黑球和1个红球的样本空间和至少摸出1个黑球的样本空间;(3)根据两个集合包含样本点的个数直观判断两个事件概率的大小.
解 (1)用树形图表示所有的结果为:
所以该试验的样本空间为Ω={ab,ac,ad,ae,bc,bd,be,cd,ce,de}.
(2)A={ac,ad,ae,bc,bd,be};
B={ab,ac,ad,ae,bc,bd,be}.
(3)因为A事件发生时,B事件一定发生,也就是说B事件发生的可能性不会比A事件发生的可能性小,因此直观上可知P(A)≤P(B).
题型突破
03
解题通法
概率意义的理解
概率是事件固有的属性,可以通过大量重复的试验得到其近似值.但在一次试验中事件发生与否都是有可能的.
题型3 随机事件的概率
当堂检测
part 04
当堂检测
04
B
当堂检测
04
C
当堂检测
04
D
当堂检测
04
B
当堂检测
04
当堂检测
04
老师名字
谢谢观看
learn to report
人教B版(2019)必修第二册
5.3.1样本空间与事件
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
了解必然现象和随机现象,了解不可能事件、必然事件及随机事件
01
理解事件与基本事件的定义,会求试验中的基本事件空间以及事件A包含的基本事件的个数
02
明确随机事件发生的概率,并能直观判断两个事件概率的大小,培养学生的逻辑推理能力
03
探索新知
part 02
探索新知
02
实例分析
如果要你将以下日常生活中的现象进行分类,你会依据什么来分?分类的结果是怎样的?
知识点1 随机现象
(1)某人练习投篮5次,结果投中了3次;
(2)每天早晨太阳都从东边升起;
(3)某人一个小时内接到10个电话;
(4)将一石块抛向空中,石块掉落下来;
(5)走到一个红绿灯路口时,前方正好是绿灯;
(6)实心铁球丢进水里,铁球会沉到水底;
(7)买一张福利彩票,没中奖.
不确定
确定
不确定
确定
不确定
确定
不确定
探索新知
02
抽象概括
请你按照上述现象的类别,分别给两类现象起个名字.
随机现象:一定条件下,发生的结果事先不能确定的现象就是随机现象(或偶然现象).
也就是说,对于随机现象而言,如果在同一条件下进行多次观察,每次观察的结果不一定相同,事先很难确定哪种结果会出现.
知识点1 随机现象
必然现象:一定条件下,发生的结果事先能确定的现象就是必然现象(或确定性现象).
探索新知
02
抽象概括
你能举出身边熟悉的随机现象和必然现象的例子吗?
知识点1 随机现象
(1)抛一枚硬币,出现正面;
(2)掷一个骰子,出现的点数为6;
(3)新生婴儿的性别为女.
(4)某地区10月份的平均气温比另一地区高;
(5)某公共汽车站某时刻的等车人数为6;
(6)从一批产品中,依次任选3件,其中恰有一等品2件;
(7)从一批灯泡中任取一只,其寿命大于10000h;
(8)电荷同性相斥,异性相吸;
(9)任意实数x,都有x≥0;
(10)明天本地下雨.
随机现象
随机现象
随机现象
随机现象
随机现象
随机现象
随机现象
必然现象
随机现象
随机现象
探索新知
02
实例分析
知识点2 样本点和样本空间
大千世界充满了随机现象,
偶然现象蕴含着必然的规律.
随机现象
生活现象
观察
实验
概念一
比如:抛一枚硬币,究竟会出现正面向上还是反面向上呢?我们可以做实验,观察.
探索新知
02
实例分析
知识点2 样本点和样本空间
随机试验:在相同的条件下,对随机现象所进行的观察或实验称为随机试验(简称为试验)
随机现象
生活现象
随机试验
观察
实验
概念二
比如:抛一枚硬币,掷一个均匀的骰子等
探索新知
02
实例分析
知识点2 样本点和样本空间
随机现象
生活现象
随机试验
观察
实验
概念二
三个
条件
条 件
过 程
结 果
(1)可重复性:试验可以在相同条件下重复进行;
(2)随机性:不能预知每次试验的具体结果;
(3)确定性:试验的所有可能结果是明确可知的.
说明:对于随机试验而言,每次试验的结果如何,是无法预料的,但随着试验的重复进行,其结果的出现会呈现出一定的规律性.
探索新知
02
实例分析
知识点2 样本点和样本空间
随机现象
生活现象
随机试验
观察
实验
概念三
样本点
样本空间
三个
条件
样本点:随机试验中每一种可能出现的结果,都称为样本点.
样本空间:把由所有样本点组成的集合称为样本空间(通常用大写希腊字母Ω表示)
注:
1.样本空间的本质为一集合;
2.样本点是样本空间的元素.
探索新知
02
实例分析
请你分别指出试验:抛掷一枚硬币、掷一个骰子的样本点和样本空间.
知识点2 样本点和样本空间
(1)抛一枚硬币,如果样本点记为“正面向上”、“反面向上”,则样本空间为Ω={正面向上,反面向上}.
思考:样本点可以用更简单的方式表示吗?
如果把样本点“正面向上”、“反面向上”分别记为“1”、“0”,
则样本空间为Ω={1,0}.
(2)掷一个骰子,如果样本点用朝上的面的点数表示,则其样本空间为Ω={1,2,3,4,5,6}
探索新知
02
例1 先后抛出两枚硬币,观察正反面出现的情况,选择合适的方法表示样本点,并写出样本空间.
表示1:
用Z表示“正面朝上”;用F表示“反面朝上”.
表示2:
用1表示“正面朝上”;用0表示“反面朝上”.
表示3:
注:1.样本空间的表示需要选择简洁的方式;
2.无论是哪种符号,都要先说明符号表示的意思.
知识点2 样本点和样本空间
探索新知
02
追问:连续抛掷一枚骰子2次,观察朝上的面的点数,写出对应的样本空间;
解:对于试验,用表示抛掷的结果,其中表示第一次掷出的点数,表示第二次掷出的点数,则所有可能的结果如下表.
于是,试验共有个样本点.因此,该试验的样本空间为
这里的和是不同的样本点,分别表示连续抛掷一枚子2次,“第一次掷出的点数为1,第二次掷出的点数为 2”和“第一次掷出的点数为 2,第二次掷出的点数1”.
知识点2 样本点和样本空间
探索新知
02
追问:连续抛掷一枚骰子2次,观察朝上的面的点数,写出对应的样本空间;
解:对于试验,用表示抛掷的结果,其中表示第一次掷出的点数,表示第二次掷出的点数,则所有可能的结果如下表.
于是,试验共有个样本点.因此,该试验的样本空间为
注:从集合角度看,样本空间的表示可以有列举法和描述法,需要根据题目特点选择更为简洁的表示方法.
探索新知
02
实例分析
知识点3 随机事件
如果随机试验的样本空间为Ω,则随机事件A是Ω的一个非空真子集.
若试验的结果是A中的元素,则称A发生(或出现);否则,称A不发生(或不出现).
随机事件也可用自然语言描述.
探索新知
02
实例分析
掷一个骰子,观察朝上的面的点数,则样本空间Ω={1,2,3,4,5,6}.
思考:(1)事件A=“出现的点数为奇数”如何用集合语言来描述?如何用维恩图直观描述?
(1)事件A=“出现的点数为奇数”用集合语言表示为A={1,3,5},A是一个随机事件.
用韦恩图来直观地表示事件,如右图:
Ω
A
知识点3 随机事件
探索新知
02
实例分析
掷一个骰子,观察朝上的面的点数,则样本空间Ω={1,2,3,4,5,6}.
思考:(2)同学们分成小组,举例写出一些随机事件,用集合语言和自然语言两种方式来描述.
(2)B={2,4,6},B表示随机事件“出现的点数为偶数”.
如果掷骰子得到的点数为3,则可知上述随机事件A发生且随机事件B不发生.
知识点3 随机事件
探索新知
02
抽象概括
必然事件:任何一次随机试验的结果,一定是样本空间Ω中的元素,因此,可以认为每次实验中Ω一定发生,从而称Ω为必然事件.
知识点3 随机事件
不可能事件:因为空集不包含任何样本点,因此可以认为每次试验中一定不发生,从而称不可能事件.
事件:一般地,不可能事件、随机事件、必然事件都可简称为事件,通常用大写英文字母A,B,C,···来表示事件.因为事件一定是样本空间的子集,从而可以用表示集合的韦恩图来直观地表示事件,如图.
特别地,只含有一个样本点的事件称为基本事件.
Ω
A
探索新知
02
思考交流
对基本事件的理解
(2)基本事件的概念可类比集合中元素的概念,试验可能发生的全部结果是一个集合,其元素是基本事件,基本事件不能分解,不能同时发生(相当于集合中元素的互异性)
知识点3 随机事件
(1)基本事件具有如下性质:①不能再分解的最简单的随机事件;②不同的基本事件不可能同时发生.
(3)事件与基本事件的区别:基本事件是试验中不能再分解的最简单的随机事件,而事件可以由若干个基本事件组成.
探索新知
02
例2 张华练习投篮10次,观察张华投篮命中的次数,写出对应的样本空间,并用集合表示出事件A:投篮命中的次数不少于7次.
样本空间为Ω={0,1,2,3,4,5,6,7,8,9,10}
所要表示的事件为A={7,8,9,10}
知识点3 随机事件
例3 从含有3件次品的100件产品中任取5件,观察其中次品数,写出对应的样本空间,并说明事件A={0}的实际意义.
样本空间为Ω={0,1,2,3}
事件A={0}表示的实际意义是:抽取的5件产品中,没有次品
探索新知
02
抽象概括
知识点4 随机事件发生的概念
我们已经知道,事件发生的可能性大小可以用该事件发生的概率(也简称为事件的概率)来衡量,概率越大,代表越有可能发生.事件A发生的概率通常用P(A)表示.
在例3中,事件B ={4}是不可能事件,即B=,
我们将不可能事件发生的概率规定为0,将必然事件发生的概率规定为1,即
P()=0,P(Ω)=1
你认为任意事件发生的概率应该满足什么条件?说明理由.
对于任意事件A来说,显然应该有P(Φ)≤P(A)≤P(Ω),
因此P(A)应该满足不等式0≤P(A)≤1.
探索新知
02
例4 先后两次掷一个均匀的骰子,观察朝上的面的点数.
(1)写出对应的样本空间;
(2)用集合表示事件A:点数之和为3,事件B:点数之和不超过3;
(3)从直观上判断P(A)和P(B)的大小(指出P(A)≥P(B)或P(A)≤P(B)即可).
(1)用(1,2)表示第一次掷出1点,第二次掷出2点,其他的样本点用类似的方法表示,则可知所有样本点均可表示成(i,j)的形式,其中i,j都是1,2,3,4,5,6中的数.因此,样本空间Ω={(i,j)|1≤i≤6,1≤j≤6,i∈N,j∈N}
也可简写为Ω={(i,j)|i,j=1,2,3,4,5,6}
知识点4 随机事件发生的概念
(2)A={(1,2),(2,1)},B={(1,1),(1,2),(2,1)}
(3)P(A)≤P(B)
题型突破
part 03
题型突破
03
题型1 样本点与样本空间
例1 同时转动如图所示的两个转盘,记转盘甲得到的数为x,转盘乙得到的数为y,结果记为(x,y).
①写出这个试验的样本空间;
②求这个试验的样本点的总数;
③“x+y=5”这一事件包含哪几个样本点
“x<3,且y>1”呢
④“xy=4”这一事件包含哪几个样本点 “x=y”呢
分析解答本题要根据日常生活的经验,逐个列出所要求的结果.
解:①Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),
(4,2),(4,3),(4,4)}.
②样本点的总数为16.
③“x+y=5”包含以下4个样本点:(1,4),(2,3),(3,2),(4,1).
“x<3,且y>1”包含以下6个样本点:(1,2),(1,3),(1,4),(2,2),(2,3),(2,4).
④“xy=4”包含以下3个样本点:(1,4),(2,2),(4,1).
“x=y”包含以下4个样本点:(1,1),(2,2),(3,3),(4,4).
题型突破
03
解题通法
随机事件的结果是相对于条件而言的,要确定样本空间,
(1)必须明确事件发生的条件;
(2)根据题意,按一定的次序列出所有样本点.
特别要注意结果出现的机会是均等的,按规律去写,要做到既不重复也不遗漏.
题型1 样本点与样本空间
题型突破
03
题型1 样本点与样本空间
延伸探究 1:将例1中条件不变,改为求“x+y是偶数”这一事件包含哪些样本点
解: “x+y是偶数”包括两种情况:①x,y都是奇数;②x,y都是偶数,故“x+y是偶数”这一事件包含以下8个样本点:(1,1),(1,3),(3,1),(3,3),(2,2),(2,4),(4,2),(4,4).
延伸探究 2:在例1的条件下,“xy是偶数”这一事件是必然事件吗
解:当x,y均是奇数时,xy是奇数;当x,y中至少有一个是偶数时,xy是偶数,故“xy是偶数”这一事件是随机事件,而不是必然事件.
题型突破
03
题型2 事件类型的判断
例2判断下列事件哪些是必然事件,哪些是不可能事件,哪些是随机事件.
(1)“在地球上抛一石块,下落”;
(2)“在标准大气压下,温度低于0 ℃时,冰融化”;
(3)“某人射击一次,中靶”;
(4)“如果a>b,那么a-b>0”;
(5)“掷一枚硬币,出现正面”;
(6)“导体通电后,发热”;
(7)“从分别标有号数1,2,3,4,5的5张标签中任取一张,得到4号签”;
(8)“某电话机在1分钟内收到2次呼叫”;
(9)“没有水分,种子能发芽”;
(10)“在常温下,焊锡熔化”.
分析:根据在一定条件下必然事件必然发生,不可能事件不可能发生,随机事件可能发生也可能不发生判断.
解:事件(1)(4)(6)是必然事件;事件(2)(9)(10)是不可能事件;事件(3)(5)(7)(8)是随机事件.
题型突破
03
解题通法
事件类型的判断方法
要判定某事件是何种事件,首先要看清条件,因为三种事件都是相对于一定条件而言的.其次再看它是一定发生,是不一定发生,还是一定不发生.一定发生的是必然事件,不一定发生的是随机事件,一定不发生的是不可能事件.
题型2 事件类型的判断
题型突破
03
题型3 随机事件的概率
例3袋子中装有除颜色外其他均相同的编号为a,b的2个黑球和编号为c,d,e的3个红球,从中任意摸出2个球.
(1)写出该试验的样本空间;
(2)用集合表示事件A:恰好摸出1个黑球和1个红球;事件B:至少摸出1个黑球;
(3)从直观上判断P(A)和P(B)的大小.
分析:(1)可以利用树形图写出;(2)找出恰好摸出1个黑球和1个红球的样本空间和至少摸出1个黑球的样本空间;(3)根据两个集合包含样本点的个数直观判断两个事件概率的大小.
解 (1)用树形图表示所有的结果为:
所以该试验的样本空间为Ω={ab,ac,ad,ae,bc,bd,be,cd,ce,de}.
(2)A={ac,ad,ae,bc,bd,be};
B={ab,ac,ad,ae,bc,bd,be}.
(3)因为A事件发生时,B事件一定发生,也就是说B事件发生的可能性不会比A事件发生的可能性小,因此直观上可知P(A)≤P(B).
题型突破
03
解题通法
概率意义的理解
概率是事件固有的属性,可以通过大量重复的试验得到其近似值.但在一次试验中事件发生与否都是有可能的.
题型3 随机事件的概率
当堂检测
part 04
当堂检测
04
B
当堂检测
04
C
当堂检测
04
D
当堂检测
04
B
当堂检测
04
当堂检测
04
老师名字
谢谢观看
learn to report
