5.3.2事件之间的关系与运算(教学课件)——高中数学人教B版(2019)必修第二册(共45张PPT)
文档属性
| 名称 | 5.3.2事件之间的关系与运算(教学课件)——高中数学人教B版(2019)必修第二册(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 57.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-26 00:00:00 | ||
图片预览











文档简介
人教B版(2019)必修第二册
5.3.2事件之间的关系与运算
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
Parent Conference Directory
壹
叁
贰
肆
学习目标
PART 01
学习目标
01
了解事件之间的包含关系和相等关系
01
理解互斥事件与对立事件的概念与关系
02
会用互斥事件与对立事件的概率公式求概率
03
了解并事件与交事件的概念,会进行事件的运算
04
探索新知
PART 02
探索新知
02
情境与问题
某班数学建模课分成5个小组(编号为1,2,3,4,5)采用合作学习的方式进行,课堂上教师会随机选择一个小组的成果进行展示.这一试验的样本空间可记为Ω={1,2,3,4,5},
知识点1 事件的包含与相等
记事件E={1},F={1,2},G={1,3},H={1,2,3},I={4,5}.
问题1 说出每一事件的实际意义,并尝试理解上述各事件之间的关系.
事件 E:老师选择第 1 小组的成果进行展示;
事件 F:老师选择第 1 小组或第 2 小组的成果进行展示;
综上可知,如果事件 E 发生,那么事件 F 一定发生;即如果教师选择了第 1 组,那么“选择了第 1 组或者第 2 组”也就一定发生了.
故事件E发生,则事件F一定发生;同理事件H与事件I不能同时发生;……
探索新知
02
抽象概括
知识点1 事件的包含与相等
问题2 上节课我们理解了在事件与集合之间的对应关系,类比集合之间的关系和运算,描述上述事件之间的关系.
E?F,F∩G=E,F∪G=H,H∩I=?……
?
事件的包含:一般地,如果事件A发生时,事件B一定发生,则称“A 包含于B”(或“B包含A”)记作A?B(或B?A).如图
若A?B,则有(1)A 发生是 B 发生的充分条件,
B 发生是 A 发生的必要条件;
(2)事件 A 发生的可能性不比事件 B 发生的可能性大,
即 P(A) ≤ P(B).
A
B
探索新知
02
抽象概括
知识点1 事件的包含与相等
问题2 上节课我们理解了在事件与集合之间的对应关系,类比集合之间的关系和运算,描述上述事件之间的关系.
E?F,F∩G=E,F∪G=H,H∩I=?……
?
事件的相等:如果事件A发生时,事件B一定发生;而且事件B发生时,事件A也一定发生,则称“A与B相等”,记作A=B .
不难看出A=B ? A ? B 且 B ? A
A=B也可用充分必要的语言表述为:A发生是B发生的充要条件.
显然,当A=B时,P(A)=P(B).
探索新知
02
抽象概括
知识点1 事件的包含与相等
问题3 请你举一些实例,来理解事件的包含与相等的关系.
(1)先后抛两枚硬币,如果A表示“恰好有一枚硬币出现正面”,B表示“两枚硬币都出现正面”,C表示“至少有一枚硬币出现正面”,D表示“两枚硬币都没有出现反面”,则A?C,B?C,B=D.
(2)已知某产品是否合格包括长度、直径两个指标,如果A表示“长度不合格”,B表示“产品不合格”,则A?B;
探索新知
02
知识拓展
(1)①不可能事件记作?,任何事件都不包含不可能事件C??,即(C为任一事件)
②事件A也包含于事件A,即A?A.
?
知识点1 事件的包含与相等
(2)①两个相等事件总是同时发生或同时不发生
②所谓事件A=B,就是说事件A,B是同一事件.
③在验证两个事件是否相等时,常用到相等事件的定义.
④如果两个事件相等,那么它们的样本点完全相同
探索新知
02
抽象概括
知识点2 事件的运算
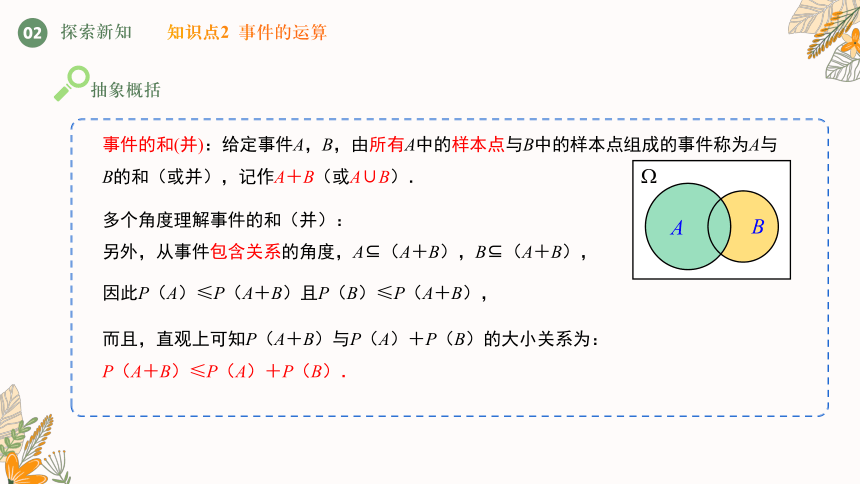
事件的和(并):给定事件A,B,由所有A中的样本点与B中的样本点组成的事件称为A与B的和(或并),记作A+B(或A∪B).
多个角度理解事件的和(并):
按照定义可知,事件A+B发生时,当且仅当事件A与事件B中至少有一个发生,即:有三种情况,即事件A发生且事件B不发生,事件A不发生且事件B发生,事件A和事件B同时发生;
事件A与B的和可以用如图所示的阴影部分表示:
B
A
探索新知
02
抽象概括
知识点2 事件的运算
事件的和(并):给定事件A,B,由所有A中的样本点与B中的样本点组成的事件称为A与B的和(或并),记作A+B(或A∪B).
多个角度理解事件的和(并):
B
A
另外,从事件包含关系的角度,A?(A+B),B?(A+B),
而且,直观上可知P(A+B)与P(A)+P(B)的大小关系为:
P(A+B)≤P(A)+P(B).
因此P(A)≤P(A+B)且P(B)≤P(A+B),
探索新知
02
抽象概括
知识点2 事件的运算
事件的积(交):给定事件A,B,由A与B中的公共样本点组成的事件称为A与B的积(或交),记作AB(或A∩B)
事件A与B的交可以用如图所示的阴影部分表示:
你能否根据事件的并(和),定义事件的积(交)
B
A
事件AB发生时,当且仅当事件A与事件B都发生;
而且,由于 AB ? A 且 AB ? B:P(AB)≤P(A),P(AB)≤P(B)
探索新知
02
抽象概括
知识点3 事件的互斥与对立
事件的互斥:给定事件A,B,若事件A与B不能同时发生,则称A与B互斥,记作AB=?(或A∩B=?).
?
事件A与B的关系可以右图表示:
在情境与问题中,事件E与I不能同时发生,从集合的角度看,它们具有什么关系?
B
A
任意两个基本事件都互斥;
?与任意事件互斥;
?
从集合的角度来看,事件A与B互斥,就意味着它们没有公共元素.
直观上可以看出,如果事件A与B互斥,则P(AB)=0;
当A与B互斥时,有P(A+B)=P(A)+P(B),这称为互斥事件的概率加法公式.
推广:一般地,如果A1,A2,……,An是两两互斥的事件,则
P(A1+A2+……+An)=P(A1)+P(A2)+……+P(An)
探索新知
02
抽象概括
知识点3 事件的互斥与对立
对立事件:给定样本空间Ω与事件A,则由样本空间中所有不属于A的样本点组成的事件称为A的对立事件,记作????,用集合的观点看,????是A在Ω中的补集.
?
事件A与B的关系可以右图表示:
前述情境与问题中,互斥的事件除了E与I,还有:F与I,G与I,H与I.其中H与I除了具有互斥关系,从多种角度来理解还具有什么特殊性?
它们的并集为全集……
A
对立事件是特殊的互斥事件,若事件A,B是对立事件,则A+B是必然事件.
探索新知
02
抽象概括
知识点3 事件的互斥与对立
对立事件:给定样本空间Ω与事件A,则由样本空间中所有不属于A的样本点组成的事件称为A的对立事件,记作????,用集合的观点看,????是A在Ω中的补集.
?
事件A与B的关系可以右图表示:
A
(1)如果B =???? ,则称 A 与 B 相互对立;
?
(2)事件 A 与???? 中,有一个发生,且只有一个发生;
?
(3)由必然事件的概率为 1,可得P(A)+P(????)=1;
?
(4)如果 A 与 B 相互对立,则 A 与 B 互斥,但反之不成立;
即“A 与 B 相互对立”是“ A 与 B 互斥”的充分不必要条件.
探索新知
02
总结
结合上述事件的关系,完成下列填空.
知识点3 事件的互斥与对立
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}事件的关系
含义
符合表示
包含
事件的和 (并)
事件的积 (交)
互斥事件
对立事件
A 发生则 B 一定发生
A ? B 或 B ? A
A 与 B 至少一个发生
A∪B 或 A + B
A 与 B 都发生
A ∩ B 或 AB
A 与 B 不能同时发生
A ∩ B = ?
A 与 B 有且只有一个发生
A ∩ B = ?,A∪B = Ω
探索新知
02
思考交流
知识点4 事件的混合运算
解释事件(A????)+(????????)的实际意义是什么?
?
由事件的和可知(A????)+(????????)表示:A????与????????的和;
?
即 A 与 B 中恰有一个发生.
实际意义:
事件的和用“或”连接,表示至少有一个发生;
事件的积用“且”连接,表示都发生.
A 发生
且
B 不发生
A 不发生
且
B 发生
或
(A????)
?
(????????)
?
探索新知
02
归纳总结
事件的三种运算,求两个事件的和,求两个事件的积,求一个事件的对立事件.
事件运算的结果仍是事件,因此可以进行事件的混合运算
同数的加、减、乘、除一样,事件的混合运算也有优先级.
我们规定:求积运算的优先级高于求和运算;
因此,(A????)+(????????)可简写为A????+????????
?
知识点4 事件的混合运算
探索新知
02
例1 设A,B为两个事件,试用A,B表示下列各事件:
(1)A,B两个事件中至少有一个发生;
(2)A事件发生且B事件不发生;
(3)A,B两个事件都不发生.
解:(1)按照定义有A+B.
(2)因为B不发生可以表示为????,因此可以写成A????.
?
(3)按照定义有?????????
?
知识点4 事件的混合运算
探索新知
02
归纳总结
设A,B,C表示三个随机事件,请将下列事件用A,B,C表示出来:
知识点4 事件的混合运算
(1)A发生,B,C不发生;
(2) A,B都发生,C不发生;
(3)三个事件都发生;
(4)三个事件至少有一个发生;
(5)三个事件都不发生;
(6)不多于一个事件发生.
ABC
探索新知
02
例2 已知数学考试中,李明成绩高于90分的概率为0.3,不低于60分且不高于90分的概率为0.5,求:(1)李明成绩不低于60分的概率;
(2)李明成绩低于60分的概率.
解:记事件A:李明成绩高于90分,B:李明成绩不低于60分且不高于90分,则不难看出A与B互斥,且P(A)=0.3,P(B)=0.5.
(1)因为“李明成绩不低于60分”可表示为A+B,由A与B互斥可知P(A+B)=P(A)+P(B)=0.3+0.5=0.8.
(2)因为“李明成绩低于60分”可表示为????+????,因此
????(????+????
探索新知
02
拓展延伸
对于事件A,B,有P(A+B)≤P(A)+P(B),只有当事件A,B互斥时,等号才成立
(1)A,B不互斥时,P(A+B)<P(A)+P(B)且P(A+B)=P(A)+P(B)-P(AB).
(2)一般事件的概率加法公式,即P(A+B)=P(A)+P(B)-P(AB),
当A,B互斥时,AB=?,P(?)=0,可见互斥事件的概率加法公式满足一般事件的概率加法公式.
?
(3)若A ? B ,则P(A)≤P(B)
知识点4 事件的混合运算
题型突破
PART 03
题型突破
03
题型1 互斥事件与对立事件的判定
例1 已知某医院的急诊室有3名男医生和2名女医生,从中任选2名去参加培训.判断下列各对事件是不是互斥事件,是不是对立事件.并说明理由.
(1)“恰有1名男医生”和“恰有2名男医生”;
(2)“至少有1名男医生”和“至少有1名女医生”;
(3)“至少有1名男医生”和“全是男医生”;
(4)“至少有1名男医生”和“全是女医生”.
解 :(1)是互斥事件,但不是对立事件.
理由:所选的2名医生中,“恰有1名男医生”实质选出的是“1名男医生和1名女医生”,它与“恰有2名男医生”不可能同时发生,所以是互斥事件,同时,不能保证其中必有一个发生,因为还可能选出“恰有2名女医生”,因此二者不对立.
(2)不是互斥事件,也不是对立事件.
理由:“至少有1名男医生”包括“1名男医生和1名女医生”与“2名都是男医生”,“至少有1名女医生”包括“1名女医生和1名男医生”与“2名都是女医生”,它们共同含有“1名男医生和1名女医生”,能够同时发生,因此不互斥也不对立.
题型突破
03
题型1 互斥事件与对立事件的判定
例1 已知某医院的急诊室有3名男医生和2名女医生,从中任选2名去参加培训.判断下列各对事件是不是互斥事件,是不是对立事件.并说明理由.
(1)“恰有1名男医生”和“恰有2名男医生”;
(2)“至少有1名男医生”和“至少有1名女医生”;
(3)“至少有1名男医生”和“全是男医生”;
(4)“至少有1名男医生”和“全是女医生”.
(3)不是互斥事件,也不是对立事件.
理由:“至少有1名男医生”包括“1名男医生和1名女医生”与“2名都是男医生”,这与“全是男医生”能够同时发生,因此不互斥也不对立.
(4)是互斥事件,也是对立事件.
理由:“至少有1名男医生”包括“1名男医生和1名女医生”与“2名都是男医生”,它与“全是女医生”不可能同时发生,但其中必有一个发生,故它们是互斥事件,“2名医生”包含“至少有1名男医生”“全是女医生”,故它们也是对立事件.
题型突破
03
解题通法
互斥事件和对立事件的判定方法
1.利用基本概念,要判断两个事件是不是互斥事件,只需要找出各个事件所包含的所有结果,看它们之间能不能同时发生.在互斥的前提下,看两个事件中是否必有一个发生,可判断是否为对立事件.注意辨析“至少”“至多”等关键词语的含义,熟知它们对事件结果的影响.
2.利用集合观点,设事件A与B所含的结果组成的集合分别为A,B.
(1)若事件A与B互斥,则集合A∩B=?;
(2)若事件A与B对立,则集合A∩B=?且A∪B=Ω.
题型1 互斥事件与对立事件的判定
题型突破
03
题型2 事件的关系及运算
例2 在试验“甲、乙、丙三人各射击1次,观察中靶的情况”中,事件A表示随机事件“甲中靶”,事件B表示随机事件“乙中靶”,事件C表示随机事件“丙中靶”,试用A,B,C的运算表示下列随机事件:
(1)甲未中靶;
(2)甲中靶而乙未中靶;
(3)三人中只有丙未中靶;
(4)三人中至少有一人中靶;
(5)三人中恰有两人中靶.
(4)三人中至少有一人中靶:A∪B∪C.
题型突破
03
解题通法
事件运算应注意的2个问题
(1)进行事件的运算时,一是要紧扣运算的定义,二是要全面考查同一条件下的试验可能出现的全部结果,必要时可利用维恩图或列出全部的试验结果进行分析.
(2)在一些比较简单的题目中,需要判断事件之间的关系时,可以根据常识来判断.但如果遇到比较复杂的题目,就得严格按照事件之间关系的定义来推理.
题型2 事件的关系及运算
题型突破
03
题型3 互斥事件的概率
例3 在数学考试中,小明的成绩在90分以上(含90分)的概率是0.18,在80~89分的概率是0.51,在70~79分的概率是0.15,在60~69分的概率是0.09,计算小明在数学考试中取得80分以上(含80分)成绩的概率和小明考试及格(60分及60分以上)的概率.
分析:利用互斥事件的概率加法公式求解.
解 :分别记小明的考试成绩在90分以上(含90分),在80~89分,在70~79分,在60~69分为事件B,C,D,E,这四个事件是彼此互斥的.
根据互斥事件的概率的加法公式,小明的考试成绩在80分以上(含80分)的概率是P(B∪C)=P(B)+P(C)=0.18+0.51=0.69.
小明考试及格的概率为
P(B∪C∪D∪E)=P(B)+P(C)+P(D)+P(E)=0.18+0.51+0.15+0.09=0.93.
题型突破
03
解题通法
利用互斥事件的概率加法公式解题的步骤
(1)确定题中各事件彼此互斥
(2)将待求事件分解为几个互斥事件之和
(3)求互斥事件分别发生的概率
(4)利用互斥事件的概率加法公式P(A∪B)=P(A)+P(B)求出概率
题型3 互斥事件的概率
题型突破
03
题型4 对立事件的概率
例4 甲、乙两人对局,甲获胜的概率为0.30,成平局的概率为0.25,求:
(1)甲不输的概率;
(2)乙不输的概率.
解 :(1)甲不输即为甲胜或成平局,记甲胜为事件A,平局为事件B.
因为A∩B=?,所以A与B互斥,
则P(A+B)=P(A)+P(B)=0.30+0.25=0.55,
故甲不输的概率为0.55.
(2)因为甲胜即乙输,
所以甲获胜与乙不输互为对立事件,
则乙不输的概率P=1-P(A)=1-0.3=0.7.
题型突破
03
解题通法
对立事件及较负责事件概率的求法
(1)明确对立事件的概念,即事件A,B互斥,且A,B中必有一个发生
(2)直接计算概率较繁琐时,可先间接地计算其对立事件的概率,再由对立事件的概率公式求解
(3)应用对立事件的概率公式时,一定要分清事件的对立事件到底是什么,不能重复和遗漏,该公式常用于“至多”“至少”型问题的探求.
题型4 对立事件的概率
当堂检测
PART 04
当堂检测
04
D
当堂检测
04
D
当堂检测
04
当堂检测
04
BCD
当堂检测
04
ACD
当堂检测
04
611000
?
当堂检测
04
12
?
当堂检测
04
当堂检测
04
当堂检测
04
要点概括整合
事件的关系和运算
事情的关系
事件的运算
包含关系
相等关系
对立关系
互斥关系
并事件
交事件
谢谢观看
Learn to report
5.3.2事件之间的关系与运算
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
Parent Conference Directory
壹
叁
贰
肆
学习目标
PART 01
学习目标
01
了解事件之间的包含关系和相等关系
01
理解互斥事件与对立事件的概念与关系
02
会用互斥事件与对立事件的概率公式求概率
03
了解并事件与交事件的概念,会进行事件的运算
04
探索新知
PART 02
探索新知
02
情境与问题
某班数学建模课分成5个小组(编号为1,2,3,4,5)采用合作学习的方式进行,课堂上教师会随机选择一个小组的成果进行展示.这一试验的样本空间可记为Ω={1,2,3,4,5},
知识点1 事件的包含与相等
记事件E={1},F={1,2},G={1,3},H={1,2,3},I={4,5}.
问题1 说出每一事件的实际意义,并尝试理解上述各事件之间的关系.
事件 E:老师选择第 1 小组的成果进行展示;
事件 F:老师选择第 1 小组或第 2 小组的成果进行展示;
综上可知,如果事件 E 发生,那么事件 F 一定发生;即如果教师选择了第 1 组,那么“选择了第 1 组或者第 2 组”也就一定发生了.
故事件E发生,则事件F一定发生;同理事件H与事件I不能同时发生;……
探索新知
02
抽象概括
知识点1 事件的包含与相等
问题2 上节课我们理解了在事件与集合之间的对应关系,类比集合之间的关系和运算,描述上述事件之间的关系.
E?F,F∩G=E,F∪G=H,H∩I=?……
?
事件的包含:一般地,如果事件A发生时,事件B一定发生,则称“A 包含于B”(或“B包含A”)记作A?B(或B?A).如图
若A?B,则有(1)A 发生是 B 发生的充分条件,
B 发生是 A 发生的必要条件;
(2)事件 A 发生的可能性不比事件 B 发生的可能性大,
即 P(A) ≤ P(B).
A
B
探索新知
02
抽象概括
知识点1 事件的包含与相等
问题2 上节课我们理解了在事件与集合之间的对应关系,类比集合之间的关系和运算,描述上述事件之间的关系.
E?F,F∩G=E,F∪G=H,H∩I=?……
?
事件的相等:如果事件A发生时,事件B一定发生;而且事件B发生时,事件A也一定发生,则称“A与B相等”,记作A=B .
不难看出A=B ? A ? B 且 B ? A
A=B也可用充分必要的语言表述为:A发生是B发生的充要条件.
显然,当A=B时,P(A)=P(B).
探索新知
02
抽象概括
知识点1 事件的包含与相等
问题3 请你举一些实例,来理解事件的包含与相等的关系.
(1)先后抛两枚硬币,如果A表示“恰好有一枚硬币出现正面”,B表示“两枚硬币都出现正面”,C表示“至少有一枚硬币出现正面”,D表示“两枚硬币都没有出现反面”,则A?C,B?C,B=D.
(2)已知某产品是否合格包括长度、直径两个指标,如果A表示“长度不合格”,B表示“产品不合格”,则A?B;
探索新知
02
知识拓展
(1)①不可能事件记作?,任何事件都不包含不可能事件C??,即(C为任一事件)
②事件A也包含于事件A,即A?A.
?
知识点1 事件的包含与相等
(2)①两个相等事件总是同时发生或同时不发生
②所谓事件A=B,就是说事件A,B是同一事件.
③在验证两个事件是否相等时,常用到相等事件的定义.
④如果两个事件相等,那么它们的样本点完全相同
探索新知
02
抽象概括
知识点2 事件的运算
事件的和(并):给定事件A,B,由所有A中的样本点与B中的样本点组成的事件称为A与B的和(或并),记作A+B(或A∪B).
多个角度理解事件的和(并):
按照定义可知,事件A+B发生时,当且仅当事件A与事件B中至少有一个发生,即:有三种情况,即事件A发生且事件B不发生,事件A不发生且事件B发生,事件A和事件B同时发生;
事件A与B的和可以用如图所示的阴影部分表示:
B
A
探索新知
02
抽象概括
知识点2 事件的运算
事件的和(并):给定事件A,B,由所有A中的样本点与B中的样本点组成的事件称为A与B的和(或并),记作A+B(或A∪B).
多个角度理解事件的和(并):
B
A
另外,从事件包含关系的角度,A?(A+B),B?(A+B),
而且,直观上可知P(A+B)与P(A)+P(B)的大小关系为:
P(A+B)≤P(A)+P(B).
因此P(A)≤P(A+B)且P(B)≤P(A+B),
探索新知
02
抽象概括
知识点2 事件的运算
事件的积(交):给定事件A,B,由A与B中的公共样本点组成的事件称为A与B的积(或交),记作AB(或A∩B)
事件A与B的交可以用如图所示的阴影部分表示:
你能否根据事件的并(和),定义事件的积(交)
B
A
事件AB发生时,当且仅当事件A与事件B都发生;
而且,由于 AB ? A 且 AB ? B:P(AB)≤P(A),P(AB)≤P(B)
探索新知
02
抽象概括
知识点3 事件的互斥与对立
事件的互斥:给定事件A,B,若事件A与B不能同时发生,则称A与B互斥,记作AB=?(或A∩B=?).
?
事件A与B的关系可以右图表示:
在情境与问题中,事件E与I不能同时发生,从集合的角度看,它们具有什么关系?
B
A
任意两个基本事件都互斥;
?与任意事件互斥;
?
从集合的角度来看,事件A与B互斥,就意味着它们没有公共元素.
直观上可以看出,如果事件A与B互斥,则P(AB)=0;
当A与B互斥时,有P(A+B)=P(A)+P(B),这称为互斥事件的概率加法公式.
推广:一般地,如果A1,A2,……,An是两两互斥的事件,则
P(A1+A2+……+An)=P(A1)+P(A2)+……+P(An)
探索新知
02
抽象概括
知识点3 事件的互斥与对立
对立事件:给定样本空间Ω与事件A,则由样本空间中所有不属于A的样本点组成的事件称为A的对立事件,记作????,用集合的观点看,????是A在Ω中的补集.
?
事件A与B的关系可以右图表示:
前述情境与问题中,互斥的事件除了E与I,还有:F与I,G与I,H与I.其中H与I除了具有互斥关系,从多种角度来理解还具有什么特殊性?
它们的并集为全集……
A
对立事件是特殊的互斥事件,若事件A,B是对立事件,则A+B是必然事件.
探索新知
02
抽象概括
知识点3 事件的互斥与对立
对立事件:给定样本空间Ω与事件A,则由样本空间中所有不属于A的样本点组成的事件称为A的对立事件,记作????,用集合的观点看,????是A在Ω中的补集.
?
事件A与B的关系可以右图表示:
A
(1)如果B =???? ,则称 A 与 B 相互对立;
?
(2)事件 A 与???? 中,有一个发生,且只有一个发生;
?
(3)由必然事件的概率为 1,可得P(A)+P(????)=1;
?
(4)如果 A 与 B 相互对立,则 A 与 B 互斥,但反之不成立;
即“A 与 B 相互对立”是“ A 与 B 互斥”的充分不必要条件.
探索新知
02
总结
结合上述事件的关系,完成下列填空.
知识点3 事件的互斥与对立
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}事件的关系
含义
符合表示
包含
事件的和 (并)
事件的积 (交)
互斥事件
对立事件
A 发生则 B 一定发生
A ? B 或 B ? A
A 与 B 至少一个发生
A∪B 或 A + B
A 与 B 都发生
A ∩ B 或 AB
A 与 B 不能同时发生
A ∩ B = ?
A 与 B 有且只有一个发生
A ∩ B = ?,A∪B = Ω
探索新知
02
思考交流
知识点4 事件的混合运算
解释事件(A????)+(????????)的实际意义是什么?
?
由事件的和可知(A????)+(????????)表示:A????与????????的和;
?
即 A 与 B 中恰有一个发生.
实际意义:
事件的和用“或”连接,表示至少有一个发生;
事件的积用“且”连接,表示都发生.
A 发生
且
B 不发生
A 不发生
且
B 发生
或
(A????)
?
(????????)
?
探索新知
02
归纳总结
事件的三种运算,求两个事件的和,求两个事件的积,求一个事件的对立事件.
事件运算的结果仍是事件,因此可以进行事件的混合运算
同数的加、减、乘、除一样,事件的混合运算也有优先级.
我们规定:求积运算的优先级高于求和运算;
因此,(A????)+(????????)可简写为A????+????????
?
知识点4 事件的混合运算
探索新知
02
例1 设A,B为两个事件,试用A,B表示下列各事件:
(1)A,B两个事件中至少有一个发生;
(2)A事件发生且B事件不发生;
(3)A,B两个事件都不发生.
解:(1)按照定义有A+B.
(2)因为B不发生可以表示为????,因此可以写成A????.
?
(3)按照定义有?????????
?
知识点4 事件的混合运算
探索新知
02
归纳总结
设A,B,C表示三个随机事件,请将下列事件用A,B,C表示出来:
知识点4 事件的混合运算
(1)A发生,B,C不发生;
(2) A,B都发生,C不发生;
(3)三个事件都发生;
(4)三个事件至少有一个发生;
(5)三个事件都不发生;
(6)不多于一个事件发生.
ABC
探索新知
02
例2 已知数学考试中,李明成绩高于90分的概率为0.3,不低于60分且不高于90分的概率为0.5,求:(1)李明成绩不低于60分的概率;
(2)李明成绩低于60分的概率.
解:记事件A:李明成绩高于90分,B:李明成绩不低于60分且不高于90分,则不难看出A与B互斥,且P(A)=0.3,P(B)=0.5.
(1)因为“李明成绩不低于60分”可表示为A+B,由A与B互斥可知P(A+B)=P(A)+P(B)=0.3+0.5=0.8.
(2)因为“李明成绩低于60分”可表示为????+????,因此
????(????+????
探索新知
02
拓展延伸
对于事件A,B,有P(A+B)≤P(A)+P(B),只有当事件A,B互斥时,等号才成立
(1)A,B不互斥时,P(A+B)<P(A)+P(B)且P(A+B)=P(A)+P(B)-P(AB).
(2)一般事件的概率加法公式,即P(A+B)=P(A)+P(B)-P(AB),
当A,B互斥时,AB=?,P(?)=0,可见互斥事件的概率加法公式满足一般事件的概率加法公式.
?
(3)若A ? B ,则P(A)≤P(B)
知识点4 事件的混合运算
题型突破
PART 03
题型突破
03
题型1 互斥事件与对立事件的判定
例1 已知某医院的急诊室有3名男医生和2名女医生,从中任选2名去参加培训.判断下列各对事件是不是互斥事件,是不是对立事件.并说明理由.
(1)“恰有1名男医生”和“恰有2名男医生”;
(2)“至少有1名男医生”和“至少有1名女医生”;
(3)“至少有1名男医生”和“全是男医生”;
(4)“至少有1名男医生”和“全是女医生”.
解 :(1)是互斥事件,但不是对立事件.
理由:所选的2名医生中,“恰有1名男医生”实质选出的是“1名男医生和1名女医生”,它与“恰有2名男医生”不可能同时发生,所以是互斥事件,同时,不能保证其中必有一个发生,因为还可能选出“恰有2名女医生”,因此二者不对立.
(2)不是互斥事件,也不是对立事件.
理由:“至少有1名男医生”包括“1名男医生和1名女医生”与“2名都是男医生”,“至少有1名女医生”包括“1名女医生和1名男医生”与“2名都是女医生”,它们共同含有“1名男医生和1名女医生”,能够同时发生,因此不互斥也不对立.
题型突破
03
题型1 互斥事件与对立事件的判定
例1 已知某医院的急诊室有3名男医生和2名女医生,从中任选2名去参加培训.判断下列各对事件是不是互斥事件,是不是对立事件.并说明理由.
(1)“恰有1名男医生”和“恰有2名男医生”;
(2)“至少有1名男医生”和“至少有1名女医生”;
(3)“至少有1名男医生”和“全是男医生”;
(4)“至少有1名男医生”和“全是女医生”.
(3)不是互斥事件,也不是对立事件.
理由:“至少有1名男医生”包括“1名男医生和1名女医生”与“2名都是男医生”,这与“全是男医生”能够同时发生,因此不互斥也不对立.
(4)是互斥事件,也是对立事件.
理由:“至少有1名男医生”包括“1名男医生和1名女医生”与“2名都是男医生”,它与“全是女医生”不可能同时发生,但其中必有一个发生,故它们是互斥事件,“2名医生”包含“至少有1名男医生”“全是女医生”,故它们也是对立事件.
题型突破
03
解题通法
互斥事件和对立事件的判定方法
1.利用基本概念,要判断两个事件是不是互斥事件,只需要找出各个事件所包含的所有结果,看它们之间能不能同时发生.在互斥的前提下,看两个事件中是否必有一个发生,可判断是否为对立事件.注意辨析“至少”“至多”等关键词语的含义,熟知它们对事件结果的影响.
2.利用集合观点,设事件A与B所含的结果组成的集合分别为A,B.
(1)若事件A与B互斥,则集合A∩B=?;
(2)若事件A与B对立,则集合A∩B=?且A∪B=Ω.
题型1 互斥事件与对立事件的判定
题型突破
03
题型2 事件的关系及运算
例2 在试验“甲、乙、丙三人各射击1次,观察中靶的情况”中,事件A表示随机事件“甲中靶”,事件B表示随机事件“乙中靶”,事件C表示随机事件“丙中靶”,试用A,B,C的运算表示下列随机事件:
(1)甲未中靶;
(2)甲中靶而乙未中靶;
(3)三人中只有丙未中靶;
(4)三人中至少有一人中靶;
(5)三人中恰有两人中靶.
(4)三人中至少有一人中靶:A∪B∪C.
题型突破
03
解题通法
事件运算应注意的2个问题
(1)进行事件的运算时,一是要紧扣运算的定义,二是要全面考查同一条件下的试验可能出现的全部结果,必要时可利用维恩图或列出全部的试验结果进行分析.
(2)在一些比较简单的题目中,需要判断事件之间的关系时,可以根据常识来判断.但如果遇到比较复杂的题目,就得严格按照事件之间关系的定义来推理.
题型2 事件的关系及运算
题型突破
03
题型3 互斥事件的概率
例3 在数学考试中,小明的成绩在90分以上(含90分)的概率是0.18,在80~89分的概率是0.51,在70~79分的概率是0.15,在60~69分的概率是0.09,计算小明在数学考试中取得80分以上(含80分)成绩的概率和小明考试及格(60分及60分以上)的概率.
分析:利用互斥事件的概率加法公式求解.
解 :分别记小明的考试成绩在90分以上(含90分),在80~89分,在70~79分,在60~69分为事件B,C,D,E,这四个事件是彼此互斥的.
根据互斥事件的概率的加法公式,小明的考试成绩在80分以上(含80分)的概率是P(B∪C)=P(B)+P(C)=0.18+0.51=0.69.
小明考试及格的概率为
P(B∪C∪D∪E)=P(B)+P(C)+P(D)+P(E)=0.18+0.51+0.15+0.09=0.93.
题型突破
03
解题通法
利用互斥事件的概率加法公式解题的步骤
(1)确定题中各事件彼此互斥
(2)将待求事件分解为几个互斥事件之和
(3)求互斥事件分别发生的概率
(4)利用互斥事件的概率加法公式P(A∪B)=P(A)+P(B)求出概率
题型3 互斥事件的概率
题型突破
03
题型4 对立事件的概率
例4 甲、乙两人对局,甲获胜的概率为0.30,成平局的概率为0.25,求:
(1)甲不输的概率;
(2)乙不输的概率.
解 :(1)甲不输即为甲胜或成平局,记甲胜为事件A,平局为事件B.
因为A∩B=?,所以A与B互斥,
则P(A+B)=P(A)+P(B)=0.30+0.25=0.55,
故甲不输的概率为0.55.
(2)因为甲胜即乙输,
所以甲获胜与乙不输互为对立事件,
则乙不输的概率P=1-P(A)=1-0.3=0.7.
题型突破
03
解题通法
对立事件及较负责事件概率的求法
(1)明确对立事件的概念,即事件A,B互斥,且A,B中必有一个发生
(2)直接计算概率较繁琐时,可先间接地计算其对立事件的概率,再由对立事件的概率公式求解
(3)应用对立事件的概率公式时,一定要分清事件的对立事件到底是什么,不能重复和遗漏,该公式常用于“至多”“至少”型问题的探求.
题型4 对立事件的概率
当堂检测
PART 04
当堂检测
04
D
当堂检测
04
D
当堂检测
04
当堂检测
04
BCD
当堂检测
04
ACD
当堂检测
04
611000
?
当堂检测
04
12
?
当堂检测
04
当堂检测
04
当堂检测
04
要点概括整合
事件的关系和运算
事情的关系
事件的运算
包含关系
相等关系
对立关系
互斥关系
并事件
交事件
谢谢观看
Learn to report
