黑龙江省哈尔滨市松浦学区2023-2024学年度六年级下学期数学期末试题(PDF版,无答案)
文档属性
| 名称 | 黑龙江省哈尔滨市松浦学区2023-2024学年度六年级下学期数学期末试题(PDF版,无答案) |
|
|
| 格式 | |||
| 文件大小 | 434.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-27 11:47:13 | ||
图片预览


文档简介
姓名:
_____
班级:
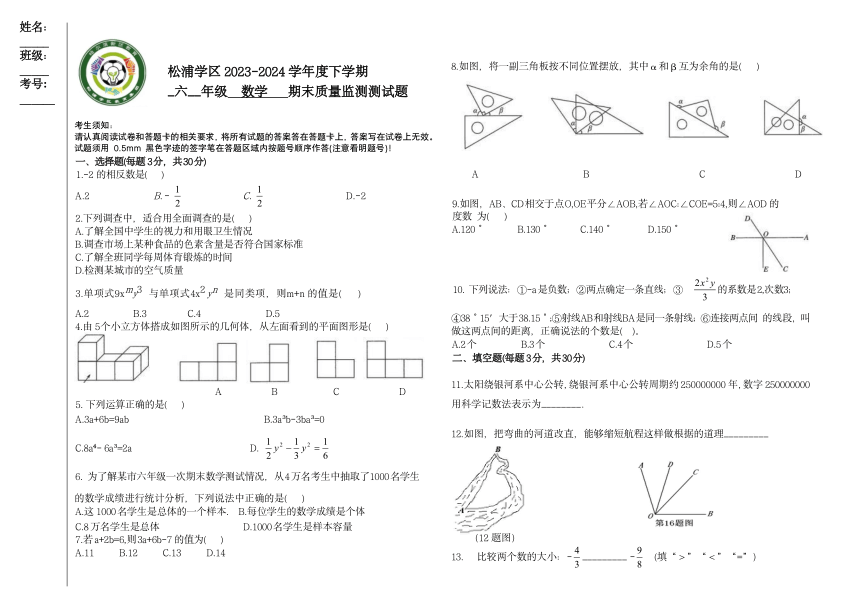
_____ 松浦学区 2023-2024 学年度下学期 8.如图,将一副三角板按不同位置摆放,其中α和β互为余角的是( )
考号:
______ _六__年级 数学 期末质量监测测试题
考生须知:
请认真阅读试卷和答题卡的相关要求,将所有试题的答案答在答题卡上,答案写在试卷上无效。
试题须用 0.5mm 黑色字迹的签字笔在答题区域内按题号顺序作答(注意看明题号)!
一、选择题(每题3分,共30分)
1.-2 的相反数是( ) A B C D
1 1
A.2 B. - C. D.-2
2 2 9.如图,AB、CD相交于点O,OE平分∠AOB,若∠AOC:∠COE=5:4,则∠AOD的
2.下列调查中,适合用全面调查的是( ) 度数 为( )
A.了解全国中学生的视力和用眼卫生情况 A.120° B.130° C.140° D.150°
B.调查市场上某种食品的色素含量是否符合国家标准
C.了解全班同学每周体育锻炼的时间
D.检测某城市的空气质量
2x 2 y
3.单项式9xmy3 与单项式4x2 yn 是同类项,则m+n 的值是( ) 10. 下列说法:①-a是负数;②两点确定一条直线;③ 的系数是2,次数3;3
A.2 B.3 C.4 D.5 ④38°15′大于38.15°;⑤射线AB和射线BA是同一条射线;⑥连接两点间 的线段,叫
4.由 5个小立方体搭成如图所示的几何体,从左面看到的平面图形是( ) 做这两点间的距离,正确说法的个数是( )。
A.2个 B.3个 C.4个 D.5个
二、填空题(每题3分,共30分)
11.太阳绕银河系中心公转,绕银河系中心公转周期约250000000年,数字250000000
A B C D
5. 下列运算正确的是( ) 用科学记数法表示为________.
A.3a+6b=9ab B.3a b-3ba =0
12.如图,把弯曲的河道改直,能够缩短航程这样做根据的道理_________
1 1 1
C.8a - 6a =2a D. y 2 y 2
2 3 6
6. 为了解某市六年级一次期末数学测试情况,从4万名考生中抽取了1000名学生
的数学成绩进行统计分析,下列说法中正确的是( )
A.这 1000名学生是总体的一个样本. B.每位学生的数学成绩是个体
C.8万名学生是总体 D.1000名学生是样本容量
7.若a+2b=6,则3a+6b-7 的值为( ) (12 题图)
A.11 B.12 C.13 D.14 4 913. 比较两个数的大小:- _________ - (填“>”“<”“=”)
3 8
14.已知∠ 与∠ 互余,且∠ =35 18′,则∠ =______° ′
23.(本题 8分)平面上有四个点 A、B、C、D,根据语句完成下面要求的
15.下午 4点 30 分时,分针与时针所成角的度数为__________ 画图。
16.如图,OC 平分∠AOB,OD 平分∠AOC,且∠COD=25°,则∠AOB= °
(1)画射线 AB与直线 CD 交于点 E;
17.飞机的无风航速是 a km/h,风速为 20km/h,飞机顺风飞行 5h,后又逆风飞行 3 (2)连接 AD、BC,它们的交点为 F;
小时,共飞行____________km. (3)连接 EF 并反向延长 EF.
18.如图所示,由一些点组成的三角形图案,每条“边”(包括两个顶点)有 n(n>1)个点,
每个图形中总的点数为 S,当 n=8 时,S= .
2
19.已知点 C在线段 AB上,AC=12cm, BC= AC.,点 M、N分别是 AC、AB的中点,
3 24.(本题 8分)某中学为了了解六年级学生体能状况,从六年级学生中随
则MN的长为 cm. 机抽取部分学生进行体能测试,测试结果分为 A、B、C、D四个等级,并
依据测试成绩绘制了如图所示的两幅尚不完整的统计图:
20.在同一平面内,已知 ∠ � = 120 ,过点 画射线 �,且满足 ∠� � 比
∠ � 2的 多 10°,OD平分∠ �,OE 平分∠� �,则∠ � = (题
3
中的角都是小于平角的角)
三、解答题(其中 21-22 题各 7分,23-24 各 8 分,25-27 各 10 分,共计 60 分。)
21、(本题 7分)计算:
(1) 2 3 3 4 ( 3) 15 1 2 3(2) 12 24 ( )
6 3 4
根据统计图提供的信息解答下列问题:
1 (1)这次抽样调查的样本容量是________,请补全条形统计图;
22、(本题 7分)先化简,再求代数式 4(x 1) 2(x2 1) (4x2 2x)的值,
2 (2)D 等级学生人数占被调查人数的百分比为________,在扇形统计图中
1 的圆心角为___________度.
其中 x 。
3 (3)该校六年级学生共有 1600 人,请你估计其中 A等级的学生人数。
2
25.(本题 10 分)某工厂从生产的袋装商品中抽出部分样品,检测每袋的质量是否
符合标准,超过或不足的部分用正数或负数表示,记录如下表:(注:该商品按克 26.(本题 10 分) 点o在直线AB上, COD EOF 90
称重出售) (1)如图 1,若射线OA是 COE的平分线, DOF 126 ,求 AOC的度数;
与标准质量的差值/克 -5 -2 0 1 3 6 (2)如图 2,延长线段FO得到射线OG,求 DOF比 COG大多少度;
袋数 1 4 3 4 5 3 (3)如图 3,在(2)的条件下
(1)这批样品中,不足标准质量的有多少袋?质量最多的与质量最少的差多少 若 DOF 4 COG, AOC 2 AOE,求 BOF的度数。
克?
(2)若每袋袋装商品的标准质量是 50 克,成本为 4元/克,则抽样检测的这批商
品的总成本多少元?
(3)在(2)问的条件下,若袋装商品正常每克加价 50%出售,为了尽快出售打
九折售卖,在售卖的过程中,还有 5%的重量损耗,求这批袋装商品全部出售后的
利润是多少元?
3
27、(本题 10 分):
如图,在数轴上 A点表示的有理数为 a,B点表示的有理数为 b,AB 表示 A点和 B
点的距离,且 a、b满足 |a—9| +(b 6)2 =0.
(1)求 a、b 的值及 A、B两点之间的距离。
(2)若动点 P从点 A出发,以每秒 3个单位长度的速度沿数轴向左匀速运动,
动点 Q从点 B出发,以每秒 2个单位长度的速度沿数轴向某个方向匀速运动。
若点 P、Q同时出发,重合后同时停止运动,运动时间为 t 秒,请用含 t 的式子
表示 PQ的长。
(3)在(2)的条件下,M是线段 PQ的中点,是否存在这样的 t 值,使线段 OM的长度
1
是 ,若存在,请求 t 的值,若不存在,请说明理由。
2
4
_____
班级:
_____ 松浦学区 2023-2024 学年度下学期 8.如图,将一副三角板按不同位置摆放,其中α和β互为余角的是( )
考号:
______ _六__年级 数学 期末质量监测测试题
考生须知:
请认真阅读试卷和答题卡的相关要求,将所有试题的答案答在答题卡上,答案写在试卷上无效。
试题须用 0.5mm 黑色字迹的签字笔在答题区域内按题号顺序作答(注意看明题号)!
一、选择题(每题3分,共30分)
1.-2 的相反数是( ) A B C D
1 1
A.2 B. - C. D.-2
2 2 9.如图,AB、CD相交于点O,OE平分∠AOB,若∠AOC:∠COE=5:4,则∠AOD的
2.下列调查中,适合用全面调查的是( ) 度数 为( )
A.了解全国中学生的视力和用眼卫生情况 A.120° B.130° C.140° D.150°
B.调查市场上某种食品的色素含量是否符合国家标准
C.了解全班同学每周体育锻炼的时间
D.检测某城市的空气质量
2x 2 y
3.单项式9xmy3 与单项式4x2 yn 是同类项,则m+n 的值是( ) 10. 下列说法:①-a是负数;②两点确定一条直线;③ 的系数是2,次数3;3
A.2 B.3 C.4 D.5 ④38°15′大于38.15°;⑤射线AB和射线BA是同一条射线;⑥连接两点间 的线段,叫
4.由 5个小立方体搭成如图所示的几何体,从左面看到的平面图形是( ) 做这两点间的距离,正确说法的个数是( )。
A.2个 B.3个 C.4个 D.5个
二、填空题(每题3分,共30分)
11.太阳绕银河系中心公转,绕银河系中心公转周期约250000000年,数字250000000
A B C D
5. 下列运算正确的是( ) 用科学记数法表示为________.
A.3a+6b=9ab B.3a b-3ba =0
12.如图,把弯曲的河道改直,能够缩短航程这样做根据的道理_________
1 1 1
C.8a - 6a =2a D. y 2 y 2
2 3 6
6. 为了解某市六年级一次期末数学测试情况,从4万名考生中抽取了1000名学生
的数学成绩进行统计分析,下列说法中正确的是( )
A.这 1000名学生是总体的一个样本. B.每位学生的数学成绩是个体
C.8万名学生是总体 D.1000名学生是样本容量
7.若a+2b=6,则3a+6b-7 的值为( ) (12 题图)
A.11 B.12 C.13 D.14 4 913. 比较两个数的大小:- _________ - (填“>”“<”“=”)
3 8
14.已知∠ 与∠ 互余,且∠ =35 18′,则∠ =______° ′
23.(本题 8分)平面上有四个点 A、B、C、D,根据语句完成下面要求的
15.下午 4点 30 分时,分针与时针所成角的度数为__________ 画图。
16.如图,OC 平分∠AOB,OD 平分∠AOC,且∠COD=25°,则∠AOB= °
(1)画射线 AB与直线 CD 交于点 E;
17.飞机的无风航速是 a km/h,风速为 20km/h,飞机顺风飞行 5h,后又逆风飞行 3 (2)连接 AD、BC,它们的交点为 F;
小时,共飞行____________km. (3)连接 EF 并反向延长 EF.
18.如图所示,由一些点组成的三角形图案,每条“边”(包括两个顶点)有 n(n>1)个点,
每个图形中总的点数为 S,当 n=8 时,S= .
2
19.已知点 C在线段 AB上,AC=12cm, BC= AC.,点 M、N分别是 AC、AB的中点,
3 24.(本题 8分)某中学为了了解六年级学生体能状况,从六年级学生中随
则MN的长为 cm. 机抽取部分学生进行体能测试,测试结果分为 A、B、C、D四个等级,并
依据测试成绩绘制了如图所示的两幅尚不完整的统计图:
20.在同一平面内,已知 ∠ � = 120 ,过点 画射线 �,且满足 ∠� � 比
∠ � 2的 多 10°,OD平分∠ �,OE 平分∠� �,则∠ � = (题
3
中的角都是小于平角的角)
三、解答题(其中 21-22 题各 7分,23-24 各 8 分,25-27 各 10 分,共计 60 分。)
21、(本题 7分)计算:
(1) 2 3 3 4 ( 3) 15 1 2 3(2) 12 24 ( )
6 3 4
根据统计图提供的信息解答下列问题:
1 (1)这次抽样调查的样本容量是________,请补全条形统计图;
22、(本题 7分)先化简,再求代数式 4(x 1) 2(x2 1) (4x2 2x)的值,
2 (2)D 等级学生人数占被调查人数的百分比为________,在扇形统计图中
1 的圆心角为___________度.
其中 x 。
3 (3)该校六年级学生共有 1600 人,请你估计其中 A等级的学生人数。
2
25.(本题 10 分)某工厂从生产的袋装商品中抽出部分样品,检测每袋的质量是否
符合标准,超过或不足的部分用正数或负数表示,记录如下表:(注:该商品按克 26.(本题 10 分) 点o在直线AB上, COD EOF 90
称重出售) (1)如图 1,若射线OA是 COE的平分线, DOF 126 ,求 AOC的度数;
与标准质量的差值/克 -5 -2 0 1 3 6 (2)如图 2,延长线段FO得到射线OG,求 DOF比 COG大多少度;
袋数 1 4 3 4 5 3 (3)如图 3,在(2)的条件下
(1)这批样品中,不足标准质量的有多少袋?质量最多的与质量最少的差多少 若 DOF 4 COG, AOC 2 AOE,求 BOF的度数。
克?
(2)若每袋袋装商品的标准质量是 50 克,成本为 4元/克,则抽样检测的这批商
品的总成本多少元?
(3)在(2)问的条件下,若袋装商品正常每克加价 50%出售,为了尽快出售打
九折售卖,在售卖的过程中,还有 5%的重量损耗,求这批袋装商品全部出售后的
利润是多少元?
3
27、(本题 10 分):
如图,在数轴上 A点表示的有理数为 a,B点表示的有理数为 b,AB 表示 A点和 B
点的距离,且 a、b满足 |a—9| +(b 6)2 =0.
(1)求 a、b 的值及 A、B两点之间的距离。
(2)若动点 P从点 A出发,以每秒 3个单位长度的速度沿数轴向左匀速运动,
动点 Q从点 B出发,以每秒 2个单位长度的速度沿数轴向某个方向匀速运动。
若点 P、Q同时出发,重合后同时停止运动,运动时间为 t 秒,请用含 t 的式子
表示 PQ的长。
(3)在(2)的条件下,M是线段 PQ的中点,是否存在这样的 t 值,使线段 OM的长度
1
是 ,若存在,请求 t 的值,若不存在,请说明理由。
2
4
同课章节目录
