2.2.1基本不等式 课件(共17张PPT)
文档属性
| 名称 | 2.2.1基本不等式 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-26 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
2.2.1基本不等式
普通高中教科书人教A版(2019)数学必修第一册
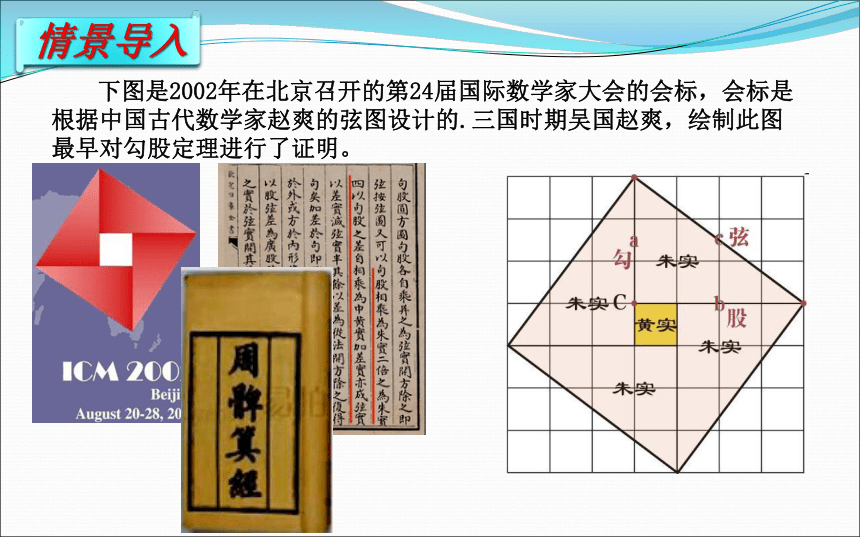
下图是2002年在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的.三国时期吴国赵爽,绘制此图最早对勾股定理进行了证明。
情景导入
A
B
C
D
H
a
b
G
F
E
B
A
C
D
E(FGH)
a
b
(a,b )
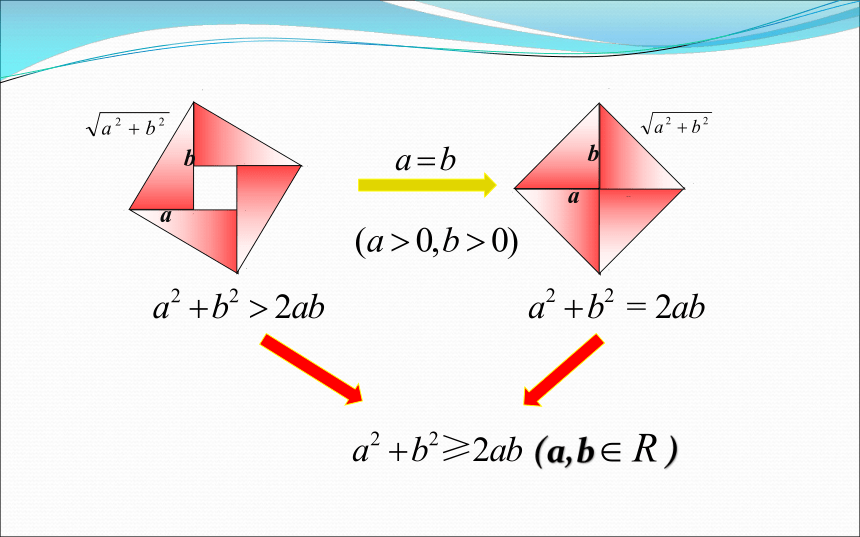
重要不 等式:
两个实数的平方和不小于它们乘积的2倍.
文字叙述:
(a,b )
如果用 、 分别代替结论中的 、 ,则 、 需要满足什么条件?
替换之后我们又会得到了什么结论呢?
探究1
通常把上式写作
证明:要证
只需证
①
只需证
②
只需证
③
③式显然成立.所以原不等式成立.
当且仅当a=b时, 原不等式中的等号成立.
分析法
证明不等式:
问题一
一、证明不等式
两正数的算术平均数不小于它们的几何平均数.
(当且仅当 时,等号成立.)
算术平均数
几何平均数
文字叙述:
基本不等式:
二、代数意义
如图,AB是圆的直径,C是AB上一点,AC=a,BC=b,过C作垂直于AB的弦DE,连接AD,BD.
D
B
A
C
a
b
由相似定理或射影定理可求出CD= ,圆的半径为
,则
探究2
O
E
半弦长
半径长
半弦长小于或等于半径长.
二、几何解释
结论
其中 叫做 的几何平均数 , 叫做 的算术平均数。
代数解释:几何平均数不大于算术平均数
几何解释:半弦不大于半径
基本不等式
若 ,则 ,(当且仅当 时取等号)
例1:判断对错
1、由 ,则 。 ( )
2、若 ,则 。 ( )
3、若 时, 。 ( )
4、函数 的最小值为 。 ( )
思考1:若x>0,y>0,且xy= 1 ,你能确定x+y的最小值?
思考2:若x>0,y>0,且x+y=2,则xy有最大值?还是最
小值?为多少?
当且仅当x=y= 1 时,等号成立
当且仅当x=y= 1 时,等号成立
a
a
若x、y均为正数,
则当x+y=S(定值)时,
当且仅当x=y时,
xy有最大值_______.
若x、y 均为正数,
则当xy=P (定值)时,
当且仅当x=y时,
x+y有最小值_______.
相等
正
定
利用基本不等式求最值时注意的问题:
③满足相等的条件.
一正,
二定,
三相等.
①两项均为正数;
②和或积为定值;
感悟
数学抽象特殊到一般直观想象数形结合分类讨论代换数形结合不等式的性质逻辑推理数学运算数学建模求最值注意:一正二定三相等直观想象变形课堂小结华罗庚寄语数缺形时少直观,形少数时难入微.数形结合百般好,隔离分家万事休.课后作业
选做题:
2.探究题:各小组查阅资料,基本不等式的其他代数几何
证明方法,整理并相互交流。
1.必做题:教科书第46页练习2,3,4,5题
(2)
(1)
方法迁移
谢谢,再见!
2.2.1基本不等式
普通高中教科书人教A版(2019)数学必修第一册
下图是2002年在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的.三国时期吴国赵爽,绘制此图最早对勾股定理进行了证明。
情景导入
A
B
C
D
H
a
b
G
F
E
B
A
C
D
E(FGH)
a
b
(a,b )
重要不 等式:
两个实数的平方和不小于它们乘积的2倍.
文字叙述:
(a,b )
如果用 、 分别代替结论中的 、 ,则 、 需要满足什么条件?
替换之后我们又会得到了什么结论呢?
探究1
通常把上式写作
证明:要证
只需证
①
只需证
②
只需证
③
③式显然成立.所以原不等式成立.
当且仅当a=b时, 原不等式中的等号成立.
分析法
证明不等式:
问题一
一、证明不等式
两正数的算术平均数不小于它们的几何平均数.
(当且仅当 时,等号成立.)
算术平均数
几何平均数
文字叙述:
基本不等式:
二、代数意义
如图,AB是圆的直径,C是AB上一点,AC=a,BC=b,过C作垂直于AB的弦DE,连接AD,BD.
D
B
A
C
a
b
由相似定理或射影定理可求出CD= ,圆的半径为
,则
探究2
O
E
半弦长
半径长
半弦长小于或等于半径长.
二、几何解释
结论
其中 叫做 的几何平均数 , 叫做 的算术平均数。
代数解释:几何平均数不大于算术平均数
几何解释:半弦不大于半径
基本不等式
若 ,则 ,(当且仅当 时取等号)
例1:判断对错
1、由 ,则 。 ( )
2、若 ,则 。 ( )
3、若 时, 。 ( )
4、函数 的最小值为 。 ( )
思考1:若x>0,y>0,且xy= 1 ,你能确定x+y的最小值?
思考2:若x>0,y>0,且x+y=2,则xy有最大值?还是最
小值?为多少?
当且仅当x=y= 1 时,等号成立
当且仅当x=y= 1 时,等号成立
a
a
若x、y均为正数,
则当x+y=S(定值)时,
当且仅当x=y时,
xy有最大值_______.
若x、y 均为正数,
则当xy=P (定值)时,
当且仅当x=y时,
x+y有最小值_______.
相等
正
定
利用基本不等式求最值时注意的问题:
③满足相等的条件.
一正,
二定,
三相等.
①两项均为正数;
②和或积为定值;
感悟
数学抽象特殊到一般直观想象数形结合分类讨论代换数形结合不等式的性质逻辑推理数学运算数学建模求最值注意:一正二定三相等直观想象变形课堂小结华罗庚寄语数缺形时少直观,形少数时难入微.数形结合百般好,隔离分家万事休.课后作业
选做题:
2.探究题:各小组查阅资料,基本不等式的其他代数几何
证明方法,整理并相互交流。
1.必做题:教科书第46页练习2,3,4,5题
(2)
(1)
方法迁移
谢谢,再见!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
