6.1分类加法计数原理与分布乘法计数原理 课件(共19张PPT)
文档属性
| 名称 | 6.1分类加法计数原理与分布乘法计数原理 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 656.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-26 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
6.1分类加法计数原理与分步乘法计数原理
探 究 1
问题1:用一个大写的英文字母或一个阿拉伯数字给教室里的一个
座位编号,总共能编出多少种不同的号码?
列举法:A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,S,Y,Z,
0,1,2,3,4,5,6,7,8,9
36
大写英文字母:26个
阿拉伯数字:10个
26+10=36
可以编出36种不同的号码
探 究
问题1:用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码?
完成一件事
方案1
用大写英文字母编号 26
方案2
用阿拉伯数字编号 10
26+10=36
给座位编号
1.分类加法计数原理
完成一件事有两类不同方案,
在第1类方案中有m种不同的方法,
在第2类方案中有n种不同的方法,
那么完成这件事共有N=m+n种不同的方法.
问题2:在填写高考志愿时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的强项专业,如表,
A大学 B大学
生物学 数学
化学 会计学
医学 经济学
物理学 法学
工程学
问:如果这名同学只能选一个专业,
那么他共有多少种选择?
探 究
A大学 B大学
生物学 数学
化学 会计学
医学 经济学
物理学 法学
工程学
完成一件事
选专业
方案1
从A大学中选专业 5
方案2
从B大学中选专业 4
探 究
A大学 B大学
生物学 数学
化学 会计学
医学 经济学
物理学 法学
工程学
C大学
营销管理
土木工程
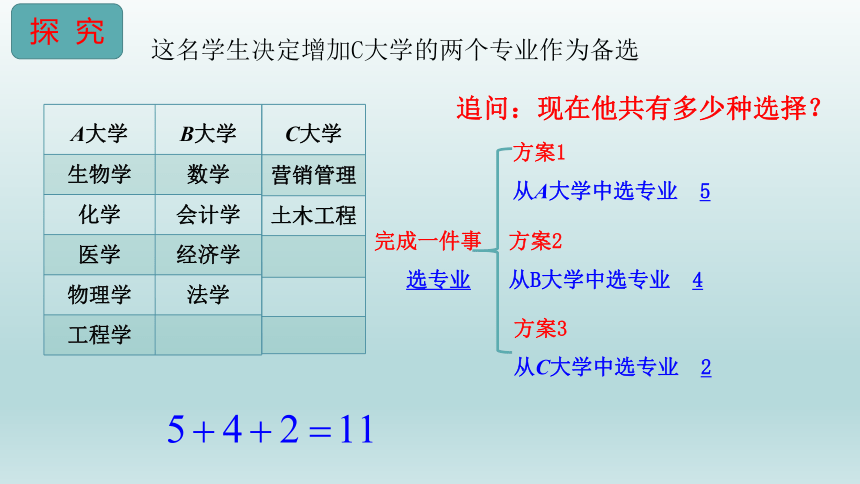
追问:现在他共有多少种选择?
这名学生决定增加C大学的两个专业作为备选
完成一件事
选专业
方案1
从A大学中选专业 5
方案2
从B大学中选专业 4
方案3
从C大学中选专业 2
完成一件事有n类不同方案,
在第1类方案中有m1种不同的方法,
在第2类方案中有m2种不同的方法,
.....
在第n类方案中有mn种不同的方法,
那么完成这件事共有N=m1+m2+……+mn种不同的方法.
分类加法计数原理推广
尝试一下:孙行者三个字交换位置可以得到多少个名字?
利用分类加法计数原理的一般步骤
分类:对完成这件事的方案进行分类,要不
重不漏;
计数:对每一类进行计数;
求和:得出总数.
探 究 2
问题3:用前6个大写的英文字母和1~9个阿拉伯数字,以A1,A2,…A9,B1,B2,…的方式给教室里的一个座位编号,总共能编出多少种不同的号码?
第1步.确定英文字母 有6种方法
第2步.确定阿拉伯数字 有9种方法
A
1
2
3
4
5
6
7
8
9
A1
A2
A3
A4
A5
A6
A7
A8
A9
9种
解决计数问题常用到“树状图”
列举法:56种
分两个步骤完成:
完成一件事
座位编号
2.分步乘法计数原理
完成一件事需要两个步骤,
做第1步有m种不同的方法,
做第2步有n种不同的方法,
那么完成这件事共有N=m×n种不同的方法.
例 题
利用分步乘法计数原理的一般步骤
分步:将完成这件事的过程分成若干步;
计数:求出每一步中的方法数;
乘积:将每一步中的方法数相乘得最终结果.
A大学 B大学
生物学 数学
化学 会计学
医学 经济学
物理学 法学
工程学
C大学
营销管理
土木工程
问:如果这名同学在每个大学选一个专业,
那么他共有多少种选择?
在填写高考志愿时,一名高中毕业生了解到,A,B,C三所大学各有一些自己感兴趣的强项专业,如表,
练习
完成一件事选专业 分3步完成:
第1步 从A大学中选专业 5
第2步从B大学中选专业 4
第3步从C大学中选专业 2
完成一件事需要n个步骤,
做第1步有m1种不同的方法,
做第2步有m2种不同的方法,
.....
做第n步有mn种不同的方法,
那么完成这件事共有N=m1×m2×……×mn种不同的方法.
分步乘法计数原理的推广
请同学们说一说分步乘法计数原理的特征
例 题
对比总结
分类加法计数原理:
完成一件事有两类不同方案,
在第1类方案中有m种不同的方法,
在第2类方案中有n种不同的方法,
那么完成这件事共有N=m+n种不同的方法.
分步乘法计数原理:
完成一件事需要两个步骤,
做第1步有m种不同的方法,
做第2步有n种不同的方法,
那么完成这件事共有N=m×n种不同的方法.
1.某校高二有三个班,分别有学生50人、50人、52人.从中选一人担任学生会主席,共有多少种不同选法( )
A.100 B.102 C.152 D.50
2.设集合A={1,2,3,4},m,n∈A,则方程 表示焦点位于x轴上的椭圆有( )
A.6个 B.8个 C.12个 D.16个
练习
3.现有4件不同款式的上衣和3条不同颜色的长裤,如果一条长裤与一件上衣配成一套,则不同的配法种数为( )
A.7 B.12 C.64 D.81
谢谢观看!
6.1分类加法计数原理与分步乘法计数原理
探 究 1
问题1:用一个大写的英文字母或一个阿拉伯数字给教室里的一个
座位编号,总共能编出多少种不同的号码?
列举法:A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,S,Y,Z,
0,1,2,3,4,5,6,7,8,9
36
大写英文字母:26个
阿拉伯数字:10个
26+10=36
可以编出36种不同的号码
探 究
问题1:用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码?
完成一件事
方案1
用大写英文字母编号 26
方案2
用阿拉伯数字编号 10
26+10=36
给座位编号
1.分类加法计数原理
完成一件事有两类不同方案,
在第1类方案中有m种不同的方法,
在第2类方案中有n种不同的方法,
那么完成这件事共有N=m+n种不同的方法.
问题2:在填写高考志愿时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的强项专业,如表,
A大学 B大学
生物学 数学
化学 会计学
医学 经济学
物理学 法学
工程学
问:如果这名同学只能选一个专业,
那么他共有多少种选择?
探 究
A大学 B大学
生物学 数学
化学 会计学
医学 经济学
物理学 法学
工程学
完成一件事
选专业
方案1
从A大学中选专业 5
方案2
从B大学中选专业 4
探 究
A大学 B大学
生物学 数学
化学 会计学
医学 经济学
物理学 法学
工程学
C大学
营销管理
土木工程
追问:现在他共有多少种选择?
这名学生决定增加C大学的两个专业作为备选
完成一件事
选专业
方案1
从A大学中选专业 5
方案2
从B大学中选专业 4
方案3
从C大学中选专业 2
完成一件事有n类不同方案,
在第1类方案中有m1种不同的方法,
在第2类方案中有m2种不同的方法,
.....
在第n类方案中有mn种不同的方法,
那么完成这件事共有N=m1+m2+……+mn种不同的方法.
分类加法计数原理推广
尝试一下:孙行者三个字交换位置可以得到多少个名字?
利用分类加法计数原理的一般步骤
分类:对完成这件事的方案进行分类,要不
重不漏;
计数:对每一类进行计数;
求和:得出总数.
探 究 2
问题3:用前6个大写的英文字母和1~9个阿拉伯数字,以A1,A2,…A9,B1,B2,…的方式给教室里的一个座位编号,总共能编出多少种不同的号码?
第1步.确定英文字母 有6种方法
第2步.确定阿拉伯数字 有9种方法
A
1
2
3
4
5
6
7
8
9
A1
A2
A3
A4
A5
A6
A7
A8
A9
9种
解决计数问题常用到“树状图”
列举法:56种
分两个步骤完成:
完成一件事
座位编号
2.分步乘法计数原理
完成一件事需要两个步骤,
做第1步有m种不同的方法,
做第2步有n种不同的方法,
那么完成这件事共有N=m×n种不同的方法.
例 题
利用分步乘法计数原理的一般步骤
分步:将完成这件事的过程分成若干步;
计数:求出每一步中的方法数;
乘积:将每一步中的方法数相乘得最终结果.
A大学 B大学
生物学 数学
化学 会计学
医学 经济学
物理学 法学
工程学
C大学
营销管理
土木工程
问:如果这名同学在每个大学选一个专业,
那么他共有多少种选择?
在填写高考志愿时,一名高中毕业生了解到,A,B,C三所大学各有一些自己感兴趣的强项专业,如表,
练习
完成一件事选专业 分3步完成:
第1步 从A大学中选专业 5
第2步从B大学中选专业 4
第3步从C大学中选专业 2
完成一件事需要n个步骤,
做第1步有m1种不同的方法,
做第2步有m2种不同的方法,
.....
做第n步有mn种不同的方法,
那么完成这件事共有N=m1×m2×……×mn种不同的方法.
分步乘法计数原理的推广
请同学们说一说分步乘法计数原理的特征
例 题
对比总结
分类加法计数原理:
完成一件事有两类不同方案,
在第1类方案中有m种不同的方法,
在第2类方案中有n种不同的方法,
那么完成这件事共有N=m+n种不同的方法.
分步乘法计数原理:
完成一件事需要两个步骤,
做第1步有m种不同的方法,
做第2步有n种不同的方法,
那么完成这件事共有N=m×n种不同的方法.
1.某校高二有三个班,分别有学生50人、50人、52人.从中选一人担任学生会主席,共有多少种不同选法( )
A.100 B.102 C.152 D.50
2.设集合A={1,2,3,4},m,n∈A,则方程 表示焦点位于x轴上的椭圆有( )
A.6个 B.8个 C.12个 D.16个
练习
3.现有4件不同款式的上衣和3条不同颜色的长裤,如果一条长裤与一件上衣配成一套,则不同的配法种数为( )
A.7 B.12 C.64 D.81
谢谢观看!
