1.3 正方形的性质与判定 专题1 中点四边形 同步练习(含答案) 2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 1.3 正方形的性质与判定 专题1 中点四边形 同步练习(含答案) 2024-2025学年北师大版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 482.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 00:00:00 | ||
图片预览


文档简介
专题1 中点四边形
类型1 中点四边形是菱形
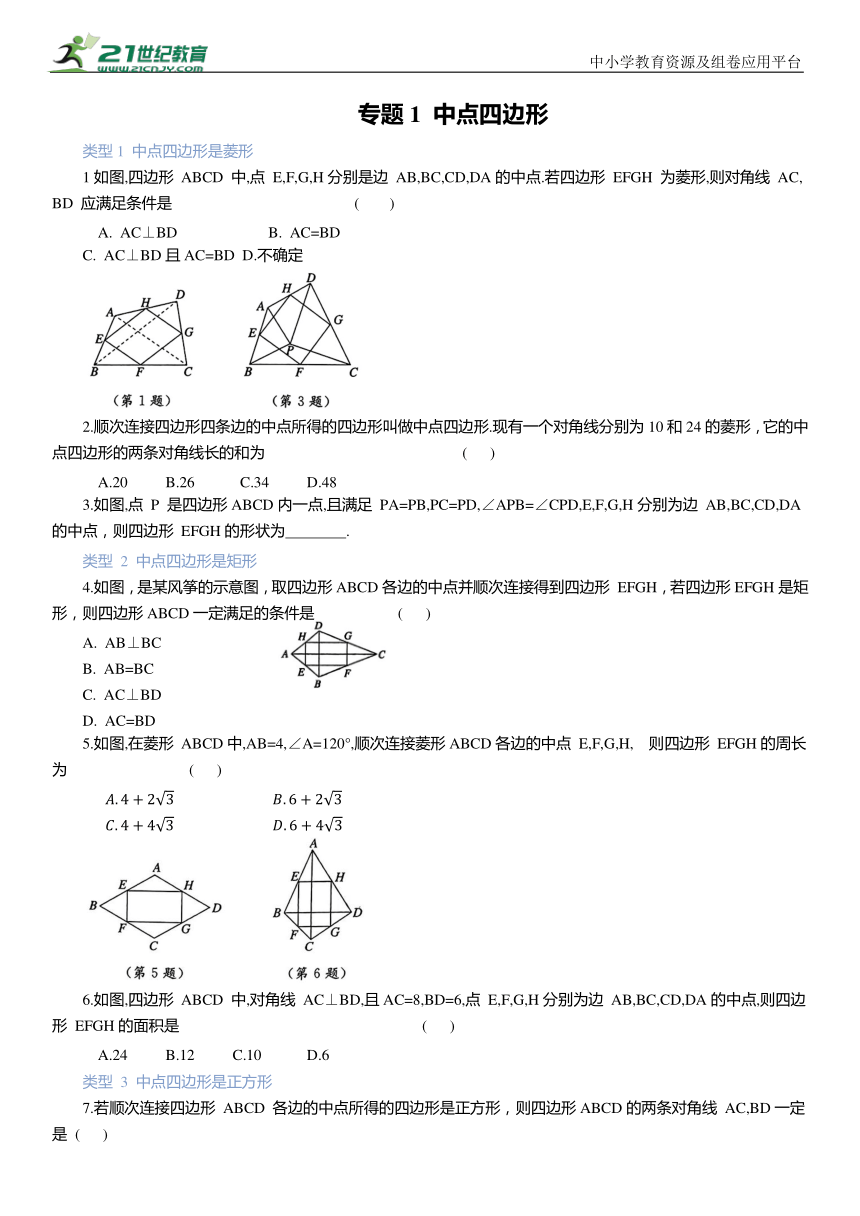
1如图,四边形 ABCD 中,点 E,F,G,H分别是边 AB,BC,CD,DA的中点.若四边形 EFGH 为菱形,则对角线 AC,BD 应满足条件是 ( )
A. AC⊥BD B. AC=BD
C. AC⊥BD且AC=BD D.不确定
2.顺次连接四边形四条边的中点所得的四边形叫做中点四边形.现有一个对角线分别为10和24的菱形,它的中点四边形的两条对角线长的和为 ( )
A.20 B.26 C.34 D.48
3.如图,点 P 是四边形ABCD内一点,且满足 PA=PB,PC=PD,∠APB=∠CPD,E,F,G,H分别为边 AB,BC,CD,DA的中点,则四边形 EFGH的形状为 .
类型 2 中点四边形是矩形
4.如图,是某风筝的示意图,取四边形ABCD各边的中点并顺次连接得到四边形 EFGH,若四边形EFGH是矩形,则四边形ABCD一定满足的条件是 ( )
A. AB⊥BC
B. AB=BC
C. AC⊥BD
D. AC=BD
5.如图,在菱形 ABCD中,AB=4,∠A=120°,顺次连接菱形ABCD各边的中点 E,F,G,H, 则四边形 EFGH的周长为 ( )
6.如图,四边形 ABCD 中,对角线 AC⊥BD,且AC=8,BD=6,点 E,F,G,H分别为边 AB,BC,CD,DA的中点,则四边形 EFGH的面积是 ( )
A.24 B.12 C.10 D.6
类型 3 中点四边形是正方形
7.若顺次连接四边形 ABCD 各边的中点所得的四边形是正方形,则四边形ABCD的两条对角线 AC,BD一定是 ( )
A.互相平分 B.互相垂直
C.互相平分且相等 D.互相垂直且相等
8对于一个四边形,我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点四边形”,如果原四边形的“中点四边形”是个正方形,我们把这个原四边形叫做“中方四边形”.下列四边形中一定是“中方四边形”的是 ( )
A.平行四边形 B.矩形
C.菱形 D.正方形
类型 4 中点四边形综合
9.如图,在四边形ABCD中,点 E,F,G,H分别是AB,BC,CD,DA边上的中点,则下列结论一定正确的是 ( )
A.四边形 EFGH 是矩形
B.四边形 EFGH的内角和小于四边形ABCD的内角和
C.四边形 EFGH 的周长等于四边形ABCD的对角线长度之和
D.四边形 EFGH 的面积等于四边形ABCD的面积
10.如图,是一组由菱形和矩形组成的图案,第1个图中菱形的面积为S(S为常数),第2个图中阴影部分是由连接菱形各边中点得到的矩形和再连接矩形各边中点得到的菱形产生的,…,依此类推,则第 2 020个图中阴影部分的面积可以用含 S的代数式(S≥2且S是正整数)表示为 ( )
11.如图,四边形ABCD的对角线AC,BD交于点O,点 M,N,P,Q分别为边 AB,BC,CD,DA的中点.有下列四个推断:
①对于任意四边形ABCD,四边形MNPQ可能不是平行四边形;
②若 AC=BD,则四边形MNPQ一定是菱形;
③若AC⊥BD,则四边形MNPQ一定是矩形;
④若四边形ABCD是菱形,则四边形MNPQ也是菱形.
其中正确的序号是 .
12. 阅读下面材料:
在数学课上,老师请同学们思考如下问题:如图①,我们把一个四边形ABCD的各边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗
小敏在思考问题时,有如下思路:连接AC.
结合小敏的思路作答.
(1)若只改变图①中四边形 ABCD的形状(如图②),则四边形 EFGH还是平行四边形吗 说明理由.
(2)如图②,在(1)的条件下,若连接AC,BD.
①当 AC 与 BD 满足什么条件时,四边形EFGH 是菱形,写出结论并证明.
②当 AC 与 BD 满足什么条件时,四边形EFGH是矩形,直接写出结论.
中小学教育资源及组卷应用平台
3 正方形的性质与判定
专题1 中点四边形
1. B 2. B
3.菱形 【点拨】如图,连接AC,BD,
∵∠APB=∠CPD,
∴∠APB +∠APD = ∠CPD +∠APD,即∠APC=∠BPD.
在△APC和△BPD中,
∴△APC≌△BPD(SAS).
∴AC=BD.
∵E,F,G,H分别为边AB,BC,CD,DA的中点,
∴EF是△BAC的中位线,EH 是△BAD的中位线,GH是△DAC的中位线.
∴EF∥AC,EF AC,GH∥AC,GH AC,EH
∴EF∥GH,EF=GH=EH.
∴四边形 EFGH 为菱形.
4. C 5. C 6. B
7. D 8. D 9. C
10. B 【点拨】观察题图发现:
第2个图形中的阴影部分的面积为S/ ,
第3个图形中的阴影部分的面积为S ,
…
第n个图形中的阴影部分的面积为
故第2020个图中阴影部分的面积可以用含 S的代数式表示为
11.②③
12.【解】(1)四边形 EFGH是平行四边形.
理由:如图,连接AC,
∵E是AB的中点,F是BC的中点,
同理
∴EF∥HG,EF=HG.
∴四边形 EFGH 是平行四边形.
(2)①当AC=BD时,四边形EFGH是菱形.证明如下:
由(1)知,四边形 EFGH是平行四边形, 且易知
∵AC=BD,∴FG=HG.
∴平行四边形 EFGH 是菱形.
②当AC⊥BD时,四边形 EFGH是矩形.
类型1 中点四边形是菱形
1如图,四边形 ABCD 中,点 E,F,G,H分别是边 AB,BC,CD,DA的中点.若四边形 EFGH 为菱形,则对角线 AC,BD 应满足条件是 ( )
A. AC⊥BD B. AC=BD
C. AC⊥BD且AC=BD D.不确定
2.顺次连接四边形四条边的中点所得的四边形叫做中点四边形.现有一个对角线分别为10和24的菱形,它的中点四边形的两条对角线长的和为 ( )
A.20 B.26 C.34 D.48
3.如图,点 P 是四边形ABCD内一点,且满足 PA=PB,PC=PD,∠APB=∠CPD,E,F,G,H分别为边 AB,BC,CD,DA的中点,则四边形 EFGH的形状为 .
类型 2 中点四边形是矩形
4.如图,是某风筝的示意图,取四边形ABCD各边的中点并顺次连接得到四边形 EFGH,若四边形EFGH是矩形,则四边形ABCD一定满足的条件是 ( )
A. AB⊥BC
B. AB=BC
C. AC⊥BD
D. AC=BD
5.如图,在菱形 ABCD中,AB=4,∠A=120°,顺次连接菱形ABCD各边的中点 E,F,G,H, 则四边形 EFGH的周长为 ( )
6.如图,四边形 ABCD 中,对角线 AC⊥BD,且AC=8,BD=6,点 E,F,G,H分别为边 AB,BC,CD,DA的中点,则四边形 EFGH的面积是 ( )
A.24 B.12 C.10 D.6
类型 3 中点四边形是正方形
7.若顺次连接四边形 ABCD 各边的中点所得的四边形是正方形,则四边形ABCD的两条对角线 AC,BD一定是 ( )
A.互相平分 B.互相垂直
C.互相平分且相等 D.互相垂直且相等
8对于一个四边形,我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点四边形”,如果原四边形的“中点四边形”是个正方形,我们把这个原四边形叫做“中方四边形”.下列四边形中一定是“中方四边形”的是 ( )
A.平行四边形 B.矩形
C.菱形 D.正方形
类型 4 中点四边形综合
9.如图,在四边形ABCD中,点 E,F,G,H分别是AB,BC,CD,DA边上的中点,则下列结论一定正确的是 ( )
A.四边形 EFGH 是矩形
B.四边形 EFGH的内角和小于四边形ABCD的内角和
C.四边形 EFGH 的周长等于四边形ABCD的对角线长度之和
D.四边形 EFGH 的面积等于四边形ABCD的面积
10.如图,是一组由菱形和矩形组成的图案,第1个图中菱形的面积为S(S为常数),第2个图中阴影部分是由连接菱形各边中点得到的矩形和再连接矩形各边中点得到的菱形产生的,…,依此类推,则第 2 020个图中阴影部分的面积可以用含 S的代数式(S≥2且S是正整数)表示为 ( )
11.如图,四边形ABCD的对角线AC,BD交于点O,点 M,N,P,Q分别为边 AB,BC,CD,DA的中点.有下列四个推断:
①对于任意四边形ABCD,四边形MNPQ可能不是平行四边形;
②若 AC=BD,则四边形MNPQ一定是菱形;
③若AC⊥BD,则四边形MNPQ一定是矩形;
④若四边形ABCD是菱形,则四边形MNPQ也是菱形.
其中正确的序号是 .
12. 阅读下面材料:
在数学课上,老师请同学们思考如下问题:如图①,我们把一个四边形ABCD的各边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗
小敏在思考问题时,有如下思路:连接AC.
结合小敏的思路作答.
(1)若只改变图①中四边形 ABCD的形状(如图②),则四边形 EFGH还是平行四边形吗 说明理由.
(2)如图②,在(1)的条件下,若连接AC,BD.
①当 AC 与 BD 满足什么条件时,四边形EFGH 是菱形,写出结论并证明.
②当 AC 与 BD 满足什么条件时,四边形EFGH是矩形,直接写出结论.
中小学教育资源及组卷应用平台
3 正方形的性质与判定
专题1 中点四边形
1. B 2. B
3.菱形 【点拨】如图,连接AC,BD,
∵∠APB=∠CPD,
∴∠APB +∠APD = ∠CPD +∠APD,即∠APC=∠BPD.
在△APC和△BPD中,
∴△APC≌△BPD(SAS).
∴AC=BD.
∵E,F,G,H分别为边AB,BC,CD,DA的中点,
∴EF是△BAC的中位线,EH 是△BAD的中位线,GH是△DAC的中位线.
∴EF∥AC,EF AC,GH∥AC,GH AC,EH
∴EF∥GH,EF=GH=EH.
∴四边形 EFGH 为菱形.
4. C 5. C 6. B
7. D 8. D 9. C
10. B 【点拨】观察题图发现:
第2个图形中的阴影部分的面积为S/ ,
第3个图形中的阴影部分的面积为S ,
…
第n个图形中的阴影部分的面积为
故第2020个图中阴影部分的面积可以用含 S的代数式表示为
11.②③
12.【解】(1)四边形 EFGH是平行四边形.
理由:如图,连接AC,
∵E是AB的中点,F是BC的中点,
同理
∴EF∥HG,EF=HG.
∴四边形 EFGH 是平行四边形.
(2)①当AC=BD时,四边形EFGH是菱形.证明如下:
由(1)知,四边形 EFGH是平行四边形, 且易知
∵AC=BD,∴FG=HG.
∴平行四边形 EFGH 是菱形.
②当AC⊥BD时,四边形 EFGH是矩形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
