专题 2 特殊平行四边形中的折叠问题 同步练习(含答案) 2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 专题 2 特殊平行四边形中的折叠问题 同步练习(含答案) 2024-2025学年北师大版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 417.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题 2 特殊平行四边形中的折叠问题
类型 1 与菱形相关的折叠问题
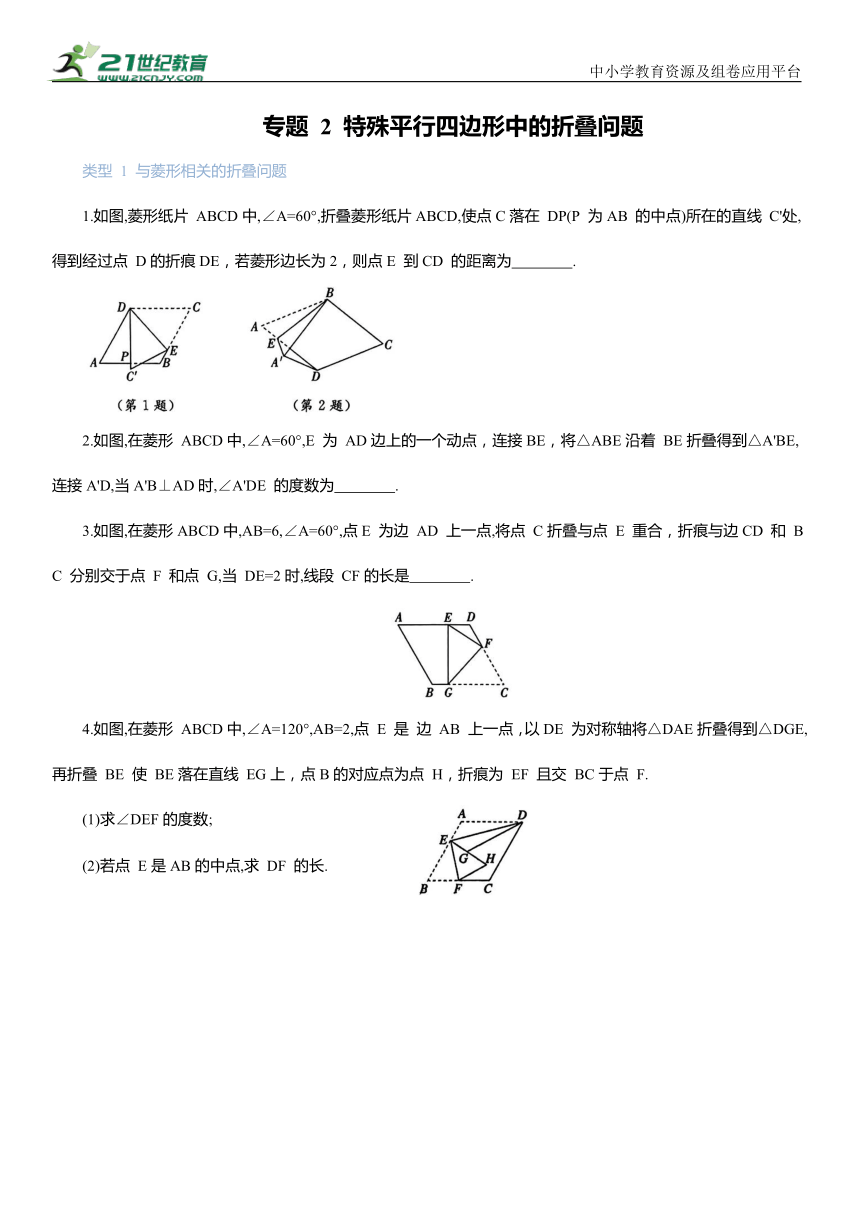
1.如图,菱形纸片 ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在 DP(P 为AB 的中点)所在的直线 C'处,得到经过点 D的折痕DE,若菱形边长为2,则点E 到CD 的距离为 .
2.如图,在菱形 ABCD中,∠A=60°,E 为 AD边上的一个动点,连接BE,将△ABE沿着 BE折叠得到△A'BE,连接A'D,当A'B⊥AD时,∠A'DE 的度数为 .
3.如图,在菱形ABCD中,AB=6,∠A=60°,点E 为边 AD 上一点,将点 C折叠与点 E 重合,折痕与边CD 和 BC 分别交于点 F 和点 G,当 DE=2时,线段 CF的长是 .
4.如图,在菱形 ABCD中,∠A=120°,AB=2,点 E 是 边 AB 上一点,以DE 为对称轴将△DAE折叠得到△DGE,再折叠 BE 使 BE落在直线 EG上,点B的对应点为点 H,折痕为 EF 且交 BC于点 F.
(1)求∠DEF的度数;
(2)若点 E是AB的中点,求 DF 的长.
类型 2 与矩形相关的折叠问题
5.把一张长方形纸片 ABCD 按如图方式折叠,使顶点 B 和 D 点重合,折痕为EF.若AB=3 cm,BC=5 cm,则A'E 的长度是 ( )
A.1.5cm B.2.4 cm C.3.4 cm D.1.6 cm
如图,点 F,G是长方形ABCD边AD上两点,点 H是边 CD上的点,连接 BF,GH,分别将△ABF,△GDH 沿 BF,GH 翻折,点 A,D 恰好都与对角线上的点 E重合,若∠ABF=24°,则∠GED= .
7如图,在平面直角坐标系中,矩形AOBC的边OB,OA分别在x轴,y轴正半轴上,点 D 在 BC 边上,将矩形 AOBC 沿 AD 折叠,点C恰好落在边OB上的点E处,若OA=8,OB=10,则点 D 的坐标是 .
类型 3 与正方形相关的折叠问题
8.如图,在正方形ABCD 中,点 E,F分别在边AB,CD上,∠EFC=120°,若将四边形 EBCF沿 EF折叠,点 B 恰好落在 AD 边上的点 B'处,则∠AEB'为 ( )
A.70° B.65° C.30° D.60°
9.如图,在正方形ABCE中,已知AB=3,DE=1,将△AED沿着 AD 翻折使得点 E,F 重合,延长DF 交 BC于G点,则 BG的长度为 ( )
A.2 B C D
10.如图,把正方形纸片 ABCD沿对边中点所在直线折叠后展开,折痕为 MN;再过点 D 折叠,使得点 A 落在 MN 上的点 F 处,折痕为DE,则 的值是 ( )
A
11如图,边长为 1 的正方形ABCD,点P 为边AD 上一动点(不与点 A重合).连接BP,将△ABP 沿直线 BP 折叠,点 A 落在点A'处,如果点 A'恰好落在正方形ABCD的对角线上,则AP的长为 .
12. 综合与实践
【操作感知】如图①,在矩形纸片 ABCD 的AD 边上取一点 P,沿 BP 折叠,使点 A 落在矩形内部点 M 处,把纸片展平,连接 PM,BM.∠DPM = 60°, 则∠MBC 的大 小 为 度.
【迁移探究】如图②,将矩形纸片换成正方形纸片,将正方形纸片 ABCD 按照【操作感知】进行折叠,并延长 PM交CD于点 Q,连接BQ.
(1)判断△MBQ 与△CBQ的关系并证明;
(2)若正方形ABCD 的边长为4,点 P 为AD 的中点,则CQ的长为 .
专题 2 特殊平行四边形中的折叠问题
【点拨】如图,连接 BD,过点 E 作 EF⊥CD 于点F,则∠EFD=90°,
∵四边形ABCD为菱形,∠A=60°,
∴易得 △ABD 为 等 边 三 角 形,∠ADC= 120°,∠C=60°,∴AD=BD,∠ADB=60°,∠CEF=30°.
∴CE=2CF,∴易得
∵P为AB 的中点,
∴DP为∠ADB的平分线,∴∠ADP=∠BDP=30°.
∴∠PDC=90°.
由折叠的性质得∠CDE=∠PDE=45°.
设 EF=x,则易得
∵菱形的边长为2,
∴CD=2.
解得
∴点E到CD的距离为
2.15° 【点拨】连接AA',BD,
∵四边形 ABCD 是菱形,
∴AB=AD.
∵∠A=60°,
∴△ABD是等边三角形.∴∠ABD=60°.
∵A'B⊥AD,
∴A'B 垂直平分AD,
∵将AB沿着BE 折叠得到A'B,
∴易得∠BAA'=75°.
3 【点拨】过点 F作FH⊥AD于H,如图所示
∵四边形 ABCD是菱形,∠A=60°, AAB=6,
∴AB=CD=6,∠EDF=120°.
∴∠FDH=60°.
设CF=x,则
由折叠的性质得EF=CF=x,
在 Rt△EFH中,
解得
4.【解】(1)由翻折可得∠AED=∠DEG,∠BEF=∠HEF,
∴∠DEG+∠HEF=∠AED+∠BEF.
∵∠DEG+∠HEF+∠AED+∠BEF=180°,
∴∠DEG+∠HEF=90°,即∠DEF=90°.
(2)∵四边形ABCD为菱形,∴AD∥BC.
∴∠A+∠B=180°,
由翻折可得 AE=EG,BE=EH,∠A=∠EGD,∠B=∠EHF.
∵点 E是AB的中点,∴AE=BE,
∴EG=EH.
即点 G 与点 H 重合.
∵∠EGD+∠EHF=∠A+∠B=180°,
∴点 D,G,F三点在同一条直线上.过点 D 作DM⊥BC,交 BC的延长线于点M.
∵A=120°,AB=2,
∴易得∠DCM=60°,CD=2.
∴∠CDM=30°,
由翻折可得 BF=FG,AD=DG=2,
设 BF=x,则MF=2-x+1=3-x,DF=2+x;
由勾股定理得( 解得
5. D 6.42°
7.(10,3) 【点拨】∵OA=8,OB=10,四边形 OACB是矩形,∴AC=OB=10,OA=BC=8.
由折叠知AE=AC=10,CD=DE.
由勾股定理得,OE=6,
∴BE=4.
设 BD=m,则CD=DE=8-m.
在 Rt△BDE中,.
解得m=3,
∴易得 D(10,3).
8. D 【点拨】∵四边形 ABCD 是正方形,
∴AB∥CD.
∴∠BEF+∠EFC=180°.
∵∠EFC=120°,
由折叠可知.
9. D 【点拨】如图,连接AG.
∵四边形ABCE为正方形,AB=3,
∴AE= AB = EC= BC= 3,∠B =∠AEC=90°.
∵DE=1,∴DC=2.
∵将△AED沿着 AD 翻折使得点 E,F重合,
∴AE=AF=3,DE=DF=1,∠E=∠AFD=90°.
∴AB=AF.
在 Rt△ABG 和 Rt△AFG中,
∴Rt△ABG≌Rt△AFG(HL).
∴BG=GF.
∴DG=DF+FG=BG+1.
在 Rt△CDG中,
10. C 【点拨】设正方形纸片 ABCD的边长为2a.
由题意可知,AM=BM=DN=NC=a,AD=DF=
MN=2a,AE=EF,∠EMF=∠DNF=90°,
设 AE=EF=x,则EM=AM-AE=u-x.
在 Rt△EMF中,∵EM +MF =EF ,
或1 【点拨】连接A'D.
①当P在A,D之间时,易得点 B,A',D 共线.
∵将△ABP 沿直线BP 折叠,点A 落在点A'处,
∵正方形 ABCD 的边长为1,
∴易得
设 AP=x,则 PD=1-x,
∴在Rt△PDA'中, 即 解得
即
②当 P 与点 D 重合时,点A'与点C 重合,亦符合题意,此时,AP=AD=1.
综上所述,AP的长为 或1.
12.【解】【操作感知】30
【迁移探究】(1)△MBQ≌△CBQ,证明如下:
由题易知AB=BM=BC,∠A=∠BMP=∠BMQ=∠C=90°,
在 Rt△MBQ 和 Rt△CBQ中,
∴Rt△MBQ≌Rt△CBQ(HL).
即△MBQ≌△CBQ.
(2 【点拨】设CQ的长为x
∵正方形ABCD的边长为4,点 P为AD 的中点,
∴DQ=4-x,AP=PD=2.由折叠可知 PM=AP=2.
由(1)可知△MBQ≌△CBQ,
∴MQ=CQ=x,
∴PQ=PM+MQ=2+x,
在 Rt△PDQ中,.
即 解得
∴CQ的长
专题 2 特殊平行四边形中的折叠问题
类型 1 与菱形相关的折叠问题
1.如图,菱形纸片 ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在 DP(P 为AB 的中点)所在的直线 C'处,得到经过点 D的折痕DE,若菱形边长为2,则点E 到CD 的距离为 .
2.如图,在菱形 ABCD中,∠A=60°,E 为 AD边上的一个动点,连接BE,将△ABE沿着 BE折叠得到△A'BE,连接A'D,当A'B⊥AD时,∠A'DE 的度数为 .
3.如图,在菱形ABCD中,AB=6,∠A=60°,点E 为边 AD 上一点,将点 C折叠与点 E 重合,折痕与边CD 和 BC 分别交于点 F 和点 G,当 DE=2时,线段 CF的长是 .
4.如图,在菱形 ABCD中,∠A=120°,AB=2,点 E 是 边 AB 上一点,以DE 为对称轴将△DAE折叠得到△DGE,再折叠 BE 使 BE落在直线 EG上,点B的对应点为点 H,折痕为 EF 且交 BC于点 F.
(1)求∠DEF的度数;
(2)若点 E是AB的中点,求 DF 的长.
类型 2 与矩形相关的折叠问题
5.把一张长方形纸片 ABCD 按如图方式折叠,使顶点 B 和 D 点重合,折痕为EF.若AB=3 cm,BC=5 cm,则A'E 的长度是 ( )
A.1.5cm B.2.4 cm C.3.4 cm D.1.6 cm
如图,点 F,G是长方形ABCD边AD上两点,点 H是边 CD上的点,连接 BF,GH,分别将△ABF,△GDH 沿 BF,GH 翻折,点 A,D 恰好都与对角线上的点 E重合,若∠ABF=24°,则∠GED= .
7如图,在平面直角坐标系中,矩形AOBC的边OB,OA分别在x轴,y轴正半轴上,点 D 在 BC 边上,将矩形 AOBC 沿 AD 折叠,点C恰好落在边OB上的点E处,若OA=8,OB=10,则点 D 的坐标是 .
类型 3 与正方形相关的折叠问题
8.如图,在正方形ABCD 中,点 E,F分别在边AB,CD上,∠EFC=120°,若将四边形 EBCF沿 EF折叠,点 B 恰好落在 AD 边上的点 B'处,则∠AEB'为 ( )
A.70° B.65° C.30° D.60°
9.如图,在正方形ABCE中,已知AB=3,DE=1,将△AED沿着 AD 翻折使得点 E,F 重合,延长DF 交 BC于G点,则 BG的长度为 ( )
A.2 B C D
10.如图,把正方形纸片 ABCD沿对边中点所在直线折叠后展开,折痕为 MN;再过点 D 折叠,使得点 A 落在 MN 上的点 F 处,折痕为DE,则 的值是 ( )
A
11如图,边长为 1 的正方形ABCD,点P 为边AD 上一动点(不与点 A重合).连接BP,将△ABP 沿直线 BP 折叠,点 A 落在点A'处,如果点 A'恰好落在正方形ABCD的对角线上,则AP的长为 .
12. 综合与实践
【操作感知】如图①,在矩形纸片 ABCD 的AD 边上取一点 P,沿 BP 折叠,使点 A 落在矩形内部点 M 处,把纸片展平,连接 PM,BM.∠DPM = 60°, 则∠MBC 的大 小 为 度.
【迁移探究】如图②,将矩形纸片换成正方形纸片,将正方形纸片 ABCD 按照【操作感知】进行折叠,并延长 PM交CD于点 Q,连接BQ.
(1)判断△MBQ 与△CBQ的关系并证明;
(2)若正方形ABCD 的边长为4,点 P 为AD 的中点,则CQ的长为 .
专题 2 特殊平行四边形中的折叠问题
【点拨】如图,连接 BD,过点 E 作 EF⊥CD 于点F,则∠EFD=90°,
∵四边形ABCD为菱形,∠A=60°,
∴易得 △ABD 为 等 边 三 角 形,∠ADC= 120°,∠C=60°,∴AD=BD,∠ADB=60°,∠CEF=30°.
∴CE=2CF,∴易得
∵P为AB 的中点,
∴DP为∠ADB的平分线,∴∠ADP=∠BDP=30°.
∴∠PDC=90°.
由折叠的性质得∠CDE=∠PDE=45°.
设 EF=x,则易得
∵菱形的边长为2,
∴CD=2.
解得
∴点E到CD的距离为
2.15° 【点拨】连接AA',BD,
∵四边形 ABCD 是菱形,
∴AB=AD.
∵∠A=60°,
∴△ABD是等边三角形.∴∠ABD=60°.
∵A'B⊥AD,
∴A'B 垂直平分AD,
∵将AB沿着BE 折叠得到A'B,
∴易得∠BAA'=75°.
3 【点拨】过点 F作FH⊥AD于H,如图所示
∵四边形 ABCD是菱形,∠A=60°, AAB=6,
∴AB=CD=6,∠EDF=120°.
∴∠FDH=60°.
设CF=x,则
由折叠的性质得EF=CF=x,
在 Rt△EFH中,
解得
4.【解】(1)由翻折可得∠AED=∠DEG,∠BEF=∠HEF,
∴∠DEG+∠HEF=∠AED+∠BEF.
∵∠DEG+∠HEF+∠AED+∠BEF=180°,
∴∠DEG+∠HEF=90°,即∠DEF=90°.
(2)∵四边形ABCD为菱形,∴AD∥BC.
∴∠A+∠B=180°,
由翻折可得 AE=EG,BE=EH,∠A=∠EGD,∠B=∠EHF.
∵点 E是AB的中点,∴AE=BE,
∴EG=EH.
即点 G 与点 H 重合.
∵∠EGD+∠EHF=∠A+∠B=180°,
∴点 D,G,F三点在同一条直线上.过点 D 作DM⊥BC,交 BC的延长线于点M.
∵A=120°,AB=2,
∴易得∠DCM=60°,CD=2.
∴∠CDM=30°,
由翻折可得 BF=FG,AD=DG=2,
设 BF=x,则MF=2-x+1=3-x,DF=2+x;
由勾股定理得( 解得
5. D 6.42°
7.(10,3) 【点拨】∵OA=8,OB=10,四边形 OACB是矩形,∴AC=OB=10,OA=BC=8.
由折叠知AE=AC=10,CD=DE.
由勾股定理得,OE=6,
∴BE=4.
设 BD=m,则CD=DE=8-m.
在 Rt△BDE中,.
解得m=3,
∴易得 D(10,3).
8. D 【点拨】∵四边形 ABCD 是正方形,
∴AB∥CD.
∴∠BEF+∠EFC=180°.
∵∠EFC=120°,
由折叠可知.
9. D 【点拨】如图,连接AG.
∵四边形ABCE为正方形,AB=3,
∴AE= AB = EC= BC= 3,∠B =∠AEC=90°.
∵DE=1,∴DC=2.
∵将△AED沿着 AD 翻折使得点 E,F重合,
∴AE=AF=3,DE=DF=1,∠E=∠AFD=90°.
∴AB=AF.
在 Rt△ABG 和 Rt△AFG中,
∴Rt△ABG≌Rt△AFG(HL).
∴BG=GF.
∴DG=DF+FG=BG+1.
在 Rt△CDG中,
10. C 【点拨】设正方形纸片 ABCD的边长为2a.
由题意可知,AM=BM=DN=NC=a,AD=DF=
MN=2a,AE=EF,∠EMF=∠DNF=90°,
设 AE=EF=x,则EM=AM-AE=u-x.
在 Rt△EMF中,∵EM +MF =EF ,
或1 【点拨】连接A'D.
①当P在A,D之间时,易得点 B,A',D 共线.
∵将△ABP 沿直线BP 折叠,点A 落在点A'处,
∵正方形 ABCD 的边长为1,
∴易得
设 AP=x,则 PD=1-x,
∴在Rt△PDA'中, 即 解得
即
②当 P 与点 D 重合时,点A'与点C 重合,亦符合题意,此时,AP=AD=1.
综上所述,AP的长为 或1.
12.【解】【操作感知】30
【迁移探究】(1)△MBQ≌△CBQ,证明如下:
由题易知AB=BM=BC,∠A=∠BMP=∠BMQ=∠C=90°,
在 Rt△MBQ 和 Rt△CBQ中,
∴Rt△MBQ≌Rt△CBQ(HL).
即△MBQ≌△CBQ.
(2 【点拨】设CQ的长为x
∵正方形ABCD的边长为4,点 P为AD 的中点,
∴DQ=4-x,AP=PD=2.由折叠可知 PM=AP=2.
由(1)可知△MBQ≌△CBQ,
∴MQ=CQ=x,
∴PQ=PM+MQ=2+x,
在 Rt△PDQ中,.
即 解得
∴CQ的长
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
