江西省吉安三中高中数学北师大版必修2第一章《垂直关系》单元测试题
文档属性
| 名称 | 江西省吉安三中高中数学北师大版必修2第一章《垂直关系》单元测试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-17 00:00:00 | ||
图片预览



文档简介
北师大版必修2第一章《垂直关系》单元测试题
班级: 姓名:
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.经过平面外两点作与此平面垂直的平面,则这样的平面( ).
A.只能作一个 B.只能作两个
C.可以作无数个 D.可作一个或无数个
2.如图,设P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( )
A. 平面PAB与平面PBC、平面PAD都垂直
B. 它们两两都垂直
C. 平面PAB与平面PBC垂直、与平面PAD不垂直
D. 平面PAB与平面PBC、平面PAD都不垂直
3. 如图等边三角形ABC的边长为1,BC边上的高为AD,若沿AD折成直二面角,则A到BC的距离是 ( )
A.1 B. C. D.
4.如图,设P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( )
A. 平面PAB与平面PBC、平面PAD都垂直
B. 它们两两都垂直
C. 平面PAB与平面PBC垂直、与平面PAD不垂直
D. 平面PAB与平面PBC、平面PAD都不垂直
5.设a、b是异面直线,下列命题正确的是( )
A.过不在a、b上的一点P一定可以作一条直线和a、b都相交
B.过不在a、b上的一点P一定可以作一个平面和a、b都垂直
C.过a一定可以作一个平面与b垂直
D.过a一定可以作一个平面与b平行
6. 设,为两个不重合的平面,、、为两两不重合的直线,给出下列四个命题:
①若∥,,则∥;
②若 , ,∥,∥,则∥;
③若∥,⊥,则⊥;
④若 ,,且⊥,⊥,则⊥.
其中正确命题的序号是( )
A.①③④ B.①②③ C.①③ D.②④
7.对两条不相交的空间直线a与b,必存在平面,使得( )
A.a ,b B.a ,b∥
C.a⊥,b⊥ D.a ,b⊥
8.空间四边形ABCD中,若AB=BC= ( http: / / www.21cnjy.com )CD=DA=AC=BC,E、F、G、H分别是AB、BC、CD、DA的中点.则四边形EFGH的形状是( )
A.平行四边形 B.长方形 C.菱形 D.正方形
9.已知平面⊥平面,∩=,点A∈,A l,直线AB∥,直线AC⊥,直线m∥,m∥,则下列四种位置关系中,不一定成立的是( )
A.AB∥m B.AC⊥m C.AB∥ D.AC⊥
10.已知平面、、,则下列命题中正确的是( )
A.⊥,⊥,则∥
B.∥,⊥,则⊥
C.∩=a,∩=b,⊥,则a⊥b
D.⊥,∩=a,a⊥b,则b⊥
二、填空题:请把答案填在题中横线上(每小题5分,共25分).
11.长方体ABCD-A1B1C1D1中,MN在平面BCC1B1内,MN⊥BC于M,则MN与AB的位置关系为_________.
12.、是两个不同的平面,、是平面、外的两条不同直线,给出四个结论:①⊥;②⊥;③⊥;④⊥.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题__________________.
13.如图所示,在四棱锥P-ABCD中,P ( http: / / www.21cnjy.com )A⊥底面ABCD.底面各边都相等,M是PC上的一动点,当点M满足______时,平面MBD⊥平面PCD.(注:只要填写一个你认为正确的即可)
14.下列五个正方体图形中,是正方体的一条对角线, 点M、N、P分别为其所在棱的中点,能得出⊥面MNP的图形的序号是________(写出所有符合要求的图形的序号).
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
15.平面的斜线AB交于点B,过定点A的动直线与AB垂直,且交于点C,则动点C的轨迹为____.(填直线、圆、其它曲线)
三、解答题:解答应写出文字说明、证明过程或演算步骤(共75分).
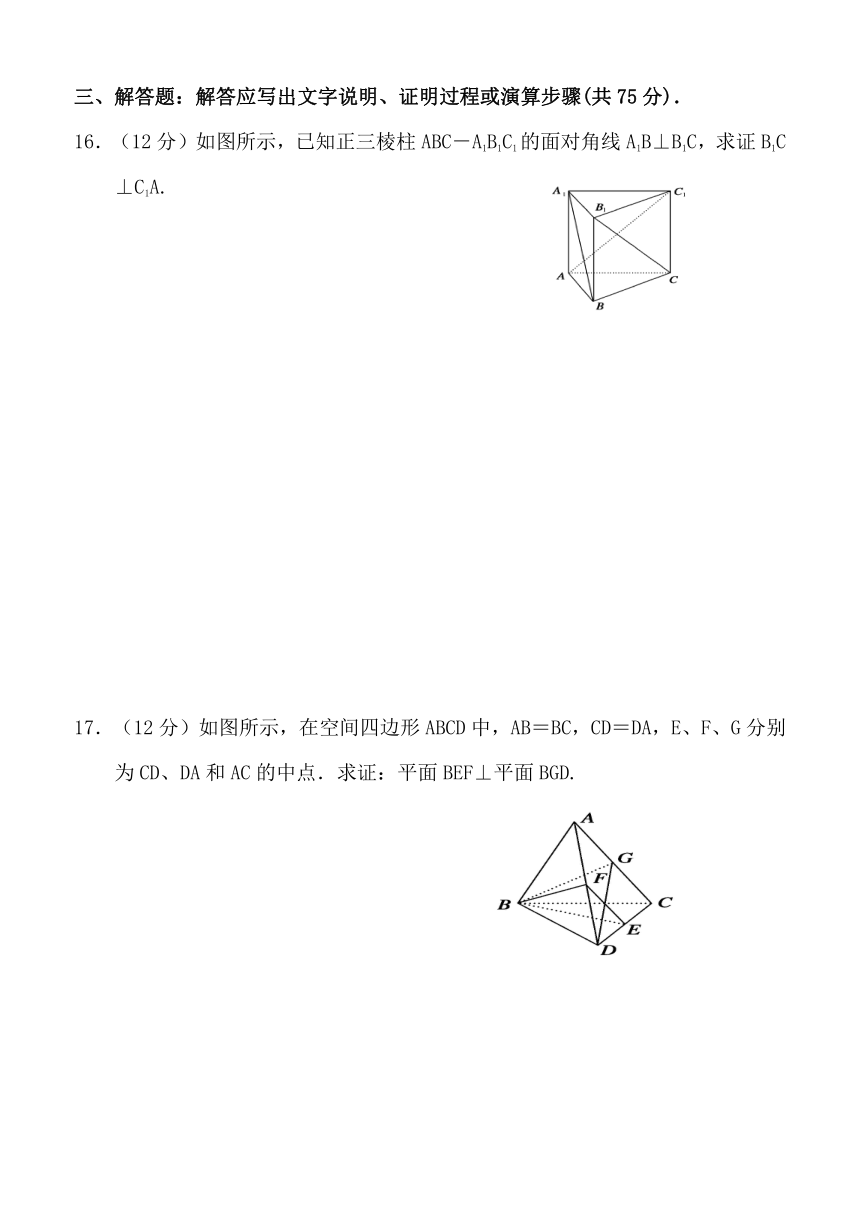
16.(12分)如图所示,已知正三棱柱ABC-A1B1C1的面对角线A1B⊥B1C,求证B1C⊥C1A.
17.(12分)如图所示,在空间四边形AB ( http: / / www.21cnjy.com )CD中,AB=BC,CD=DA,E、F、G分别为CD、DA和AC的中点.求证:平面BEF⊥平面BGD.
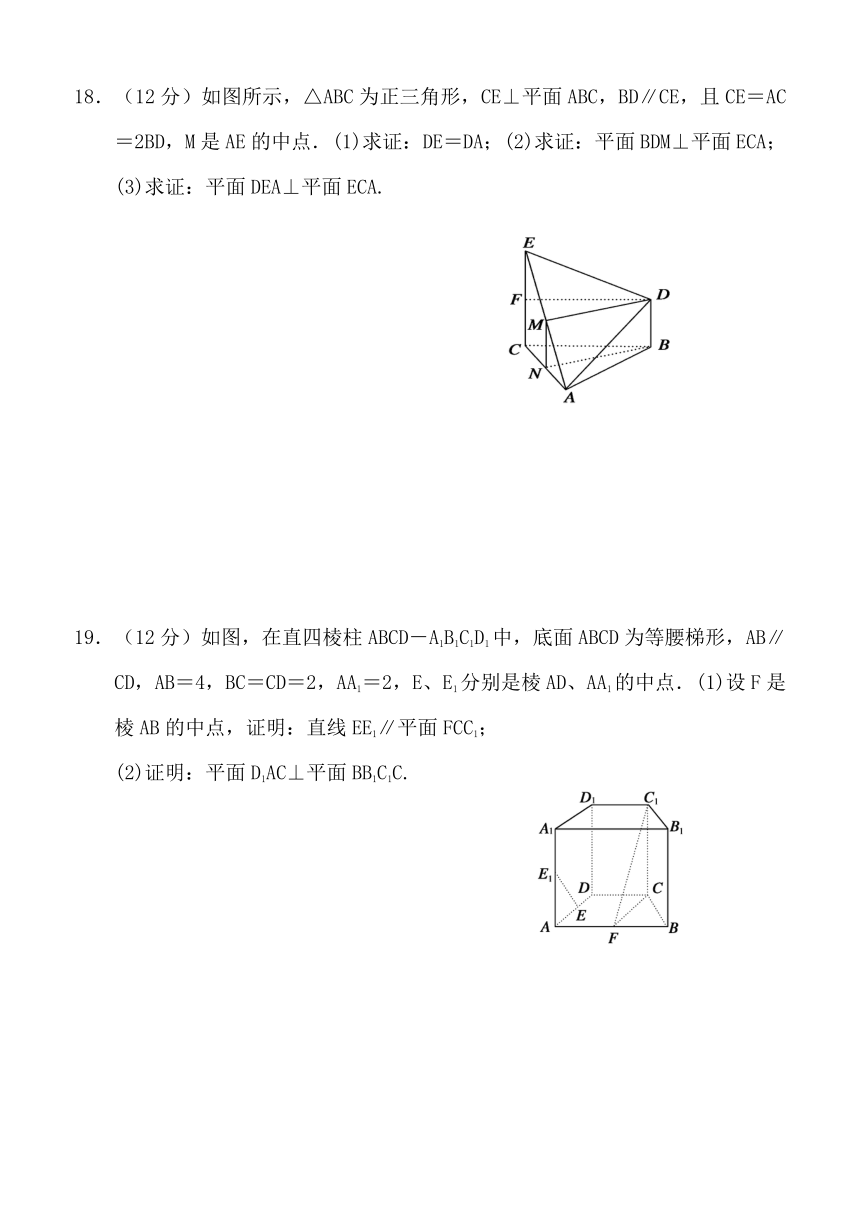
18.(12分)如图所示, ( http: / / www.21cnjy.com )△ABC为正三角形,CE⊥平面ABC,BD∥CE,且CE=AC=2BD,M是AE的中点.(1)求证:DE=DA;(2)求证:平面BDM⊥平面ECA;(3)求证:平面DEA⊥平面ECA.
19.(12分)如图,在直四棱柱ABC ( http: / / www.21cnjy.com )D-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1分别是棱AD、AA1的中点.(1)设F是棱AB的中点,证明:直线EE1∥平面FCC1;
(2)证明:平面D1AC⊥平面BB1C1C.
20.(13分)如图,在四棱锥P ( http: / / www.21cnjy.com )ABCD中,底面ABCD是边长为a的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD边的中点.(1)求证:BG⊥平面PAD;(2)求证:AD⊥PB;(3)若E为BC边的中点,能否在棱PC上找一点F,使得平面DEF⊥平面ABCD,并证明你的结论.
21.(14分)如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥ DG,EF∥DG,且AB=AD=DE=DG=2,AC=EF=1.(1)求证:BF∥平面ACGD;(2)求二面角A EG D的正切值.
北师大版必修2第一章《垂直关系》单元测试题答案
一、选择题:
1.[答案] D[解析] 当两点所在直线垂直于平面时,可作无数个;否则,有且仅有1个.
2.[答案] A[解析] 思路解析:∵PA⊥平面ABCD, ∴PA⊥BC.又
∵BC⊥AB,PA∩AB=A,∴PC⊥平面PAB,从而平面PBC⊥平面PAB.
由AD⊥PA,AD⊥AB,PA∩AB=A得AD⊥平面PAB.
∵AD平面PAD,∴平面PAD⊥平面PAB.
3. [答案] C [解析] 折叠后BD=DC=,且∠BDC为二面角的平面角, ∠BDC=90°, ∴BC=.取BC中点E,连结DE,则DE⊥BC,进一步易证AE⊥BC,AE的长为所求距离.
∵AD=,DE=BC=,∴AE=.
4.[答案]A 解析:思路解析:∵PA⊥平面ABCD, ∴PA⊥BC.又
∵BC⊥AB,PA∩AB=A,∴PC⊥平面PAB,从而平面PBC⊥平面PAB.
由AD⊥PA,AD⊥AB,PA∩AB=A得AD⊥平面PAB.
∵AD平面PAD,∴平面PAD⊥平面PAB.
5.[答案] D[解析] A不正确,若点P和直线a确定平面,当b∥时,满足条件的直线不存在;B不正确,若存在,则有a∥b,这与a、b是异面直线矛盾;C不正确,只有a、b垂直时,才能作出满足条件的平面.只有D正确.
6. [答案] C [解析] 由面面平行的判定定理,知②错误;由线面垂直的判定定理知④错误.
7.[答案] B[解析] 若a与b异面时,A、C错;当a与b不垂直时,D错,故选B.
8.[答案] D[解析] 如图所示,∵E、F、G、H分别为AB、BC、CD、DA的中点,∴EFAC,HGAC,∴四边形EFGH是平行四边形,又EH=BD,BD=AC,∴EH=EF,∴四边形EFGH是菱形.取BD中点M,连结AM、CM,∵AB=AD, ∴AM⊥BD,
又CB=CD,∴CM⊥BD,
又AM∩CM=M,∴BD⊥平面ACM,∴BD⊥AC.
又EF∥AC,BD∥EH,∴EF⊥EH,∴四边形EFGH是正方形.
9.[答案] D[解析] 本小题主要考查线面垂直、面面垂直、线线平行和线面平行.点C若在内,则有AC⊥,若不在内,则AC不垂直于,这是面面垂直的性质,故选D.
10.[答案] B[解析] 可以墙角为例知A错;B中,由⊥,由内有直线b⊥,而∥,则内有a∥b,则a⊥,⊥.
二、填空题:
11. [答案] MN⊥AB[解析] 如图所示,由长方体的性质知,平面BCC1B1⊥平面ABCD,交线为BC.
∵MN在平面BCC1B1内,且MN⊥BC,
∴MN⊥平面ABCD,而AB 平面ABCD,
∴MN⊥AB.
12.[答案] ②③④ ①(答案不惟一)
13.[答案] BM⊥PC(其它合理即可)
[解析]∵四边形ABCD的边长相等,
∴四边形为菱形.∴AC⊥BD,
又∵PA⊥面ABCD,∴PA⊥BD,∴BD⊥面PAC,∴BD⊥PC.
若PC⊥面BMD,则PC垂直于面BMD中两条相交直线.
∴当BM⊥PC时,PC⊥面BDM.∴面PCD⊥面BDM.
14. [答案]①④⑤ [解析] ( http: / / www.21cnjy.com ) ①④易判断,⑤中△PMN是正三角形且AM=AP=AN,因此,三棱锥A-PMN是正三棱锥,所以图⑤中l⊥平面MNP,由此法还可否定③.∵AM≠AP≠AN,也易否定②.
15.[答案]直线 [解析] 过点A与AB垂直的所有直线都在同一个平面内,∵AB是的斜线,∴与不平行.从而与的所有公共点都在同一条直线上,即与的交线上.从而内所有过点A与相交的直线,其交点都在此交线上.
三、解答题:
16.[解析] 如图所示,连结A1C,交AC1于点D,则点D是A1C的中点.
取BC的中点N,连结AN、DN,则DN∥A1B.
又A1B⊥B1C,∴B1C⊥DN.
又△ABC是正三角形, ∴AN⊥BC.
又平面ABC⊥平面BB1C1C,平面ABCD∩平面BB1C1C=BC,AN 平面ABC,
∴AN⊥平面BB1C1C.又B1C 平面BB1C1C,
∴B1C⊥AN.
又AN 平面AND,DN 平面AND,AN∩DN=N,
∴B1C⊥平面AND.
又C1A 平面AND,∴B1C⊥AC1.
17.[解析] ∵AB=BC,CD=AD,G是AC的中点,
∴BG⊥AC,DG⊥AC.
∴AC⊥平面BGD.又EF∥AC,
∴EF⊥平面BGD.又EF 平面BEF,
∴平面BDG⊥平面BEF.
18.[解析] (1)取EC的中点F,连结DF.
∵CE⊥平面ABC,∴CE⊥BC.
易知DF∥BC,∴CE⊥DF.
∵BD∥CE,∴BD∥平面ABC.
在Rt△EFD和Rt△DBA中,EF=CE=DB,DF=BC=AB,
∴Rt△EFD≌Rt△DBA.故DE=DA.
(2)取AC的中点N,连结MN、BN,则MNCF.
∵BDCF, ∴MNBD, ∴N∈平面BDM.
∵EC⊥平面ABC, ∴EC⊥BN.
又∵AC⊥BN,EC∩AC=C, ∴BN⊥平面ECA.
又∵BN 平面BDM, ∴平面BDM⊥平面ECA.
(3)∵DM∥BN,BN⊥平面ECA, ∴DM⊥平面ECA.
又∵DM 平面DEA,∴平面DEA⊥平面ECA.
19.[解析](1)解法一:取A1B1的中点F1,连结FF1、C1F1,
∵FF1∥BB1∥CC1,∴F1∈平面FCC1,
∴平面FCC1即为平面C1CFF1,
连结A1D、F1C,∴A1F1D1C1CD,
∴四边形A1DCF1为平行四边形,
∴A1D∥F1C.
又∵EE1∥A1D,∴EE1∥F1C,
∵EE1平面FCC1,F1C 平面FCC1,
∴EE1∥平面FCC1.
解法二:∵F为AB的中点,CD=2,AB=4,AB∥CD,
∴CDAF,∴四边形AFCD为平行四边形,∴AD∥FC.
又CC1∥DD1,FC∩CC1=C,FC 平面FCC1,CC1 平面FCC1,
∴平面ADD1A1∥平面FCC1,
又EE1 平面ADD1A1,∴EE1∥平面FCC1.
(2)证明:连结AC,在△FBC中,FC=BC=FB,
又F为AB的中点,∴AF=FC=FB,
∴∠ACB=90°,即AC⊥BC.
又AC⊥CC1,且CC1∩BC=C,
∴AC⊥平面BB1C1C,而AC 平面D1AC;
故平面D1AC⊥平面BB1C1C.
20.(1)证明:∵在菱形ABCD中,∠DAB=60°,G为AD边的中点,
∴BG⊥AD.
又∵平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD.
(2)证明:连接PG,则PG⊥AD,
由(1)得BG⊥AD,
又∵PG∩BG=G,BG平面PBG,
PG平面PBG,
∴AD⊥平面PBG.
∵PB平面PBG,∴AD⊥PB.
(3)解:当F为PC的中点时,满足平面DEF⊥平面ABCD.
证明如下:
取PC的中点F,连接DE,EF,DF,则由平面几何知识,
在△PBC中,EF∥PB,
在菱形ABCD中,GB∥DE,
而EF平面DEF,ED平面DEF,
EF∩DE=E,
PB平面PGB,GB平面PGB,
PB∩GB=B,
∴平面DEF∥平面PGB.
又∵侧面PAD为正三角形,G为AD的中点,∴PG⊥AD.
又∵侧面PAD所在平面垂直于底面ABCD,
∴PG⊥平面ABCD,而PG平面PGB,
∴平面PGB⊥平面ABCD.
故平面DEF⊥平面ABCD.
21.(1)证明:设DG的中点为M,连接AM,FM,则由已知条件易证四边形DEFM是平行四边形,
∴MF∥DE,且MF=DE.
∵平面ABC∥平面DEFG,平面ABED分别交平面ABC,平面DEFG于AB,DE,∴AB∥DE,又AB=DE,
∴MF∥AB,且MF=AB,
∴四边形ABFM是平行四边形,即BF∥AM.又BF平面ACGD,AM平面ACGD,故BF∥平面ACGD.
(2)解:连接AE,AG,EG,
∵AD⊥平面DEFG,
∴AD⊥DG,AD⊥DE.
∵AD=ED=DG,∴AE=AG.
取EG的中点H,连接AH,DH,有AH⊥EG,DH⊥EG,
则∠AHD是二面角A EG D的平面角.
∵在Rt△ADH中,由AD=DE=DG=2,得DH=.
∴tan∠AHD==,
故二面角A EG D的正切值为.
班级: 姓名:
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.经过平面外两点作与此平面垂直的平面,则这样的平面( ).
A.只能作一个 B.只能作两个
C.可以作无数个 D.可作一个或无数个
2.如图,设P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( )
A. 平面PAB与平面PBC、平面PAD都垂直
B. 它们两两都垂直
C. 平面PAB与平面PBC垂直、与平面PAD不垂直
D. 平面PAB与平面PBC、平面PAD都不垂直
3. 如图等边三角形ABC的边长为1,BC边上的高为AD,若沿AD折成直二面角,则A到BC的距离是 ( )
A.1 B. C. D.
4.如图,设P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( )
A. 平面PAB与平面PBC、平面PAD都垂直
B. 它们两两都垂直
C. 平面PAB与平面PBC垂直、与平面PAD不垂直
D. 平面PAB与平面PBC、平面PAD都不垂直
5.设a、b是异面直线,下列命题正确的是( )
A.过不在a、b上的一点P一定可以作一条直线和a、b都相交
B.过不在a、b上的一点P一定可以作一个平面和a、b都垂直
C.过a一定可以作一个平面与b垂直
D.过a一定可以作一个平面与b平行
6. 设,为两个不重合的平面,、、为两两不重合的直线,给出下列四个命题:
①若∥,,则∥;
②若 , ,∥,∥,则∥;
③若∥,⊥,则⊥;
④若 ,,且⊥,⊥,则⊥.
其中正确命题的序号是( )
A.①③④ B.①②③ C.①③ D.②④
7.对两条不相交的空间直线a与b,必存在平面,使得( )
A.a ,b B.a ,b∥
C.a⊥,b⊥ D.a ,b⊥
8.空间四边形ABCD中,若AB=BC= ( http: / / www.21cnjy.com )CD=DA=AC=BC,E、F、G、H分别是AB、BC、CD、DA的中点.则四边形EFGH的形状是( )
A.平行四边形 B.长方形 C.菱形 D.正方形
9.已知平面⊥平面,∩=,点A∈,A l,直线AB∥,直线AC⊥,直线m∥,m∥,则下列四种位置关系中,不一定成立的是( )
A.AB∥m B.AC⊥m C.AB∥ D.AC⊥
10.已知平面、、,则下列命题中正确的是( )
A.⊥,⊥,则∥
B.∥,⊥,则⊥
C.∩=a,∩=b,⊥,则a⊥b
D.⊥,∩=a,a⊥b,则b⊥
二、填空题:请把答案填在题中横线上(每小题5分,共25分).
11.长方体ABCD-A1B1C1D1中,MN在平面BCC1B1内,MN⊥BC于M,则MN与AB的位置关系为_________.
12.、是两个不同的平面,、是平面、外的两条不同直线,给出四个结论:①⊥;②⊥;③⊥;④⊥.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题__________________.
13.如图所示,在四棱锥P-ABCD中,P ( http: / / www.21cnjy.com )A⊥底面ABCD.底面各边都相等,M是PC上的一动点,当点M满足______时,平面MBD⊥平面PCD.(注:只要填写一个你认为正确的即可)
14.下列五个正方体图形中,是正方体的一条对角线, 点M、N、P分别为其所在棱的中点,能得出⊥面MNP的图形的序号是________(写出所有符合要求的图形的序号).
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
15.平面的斜线AB交于点B,过定点A的动直线与AB垂直,且交于点C,则动点C的轨迹为____.(填直线、圆、其它曲线)
三、解答题:解答应写出文字说明、证明过程或演算步骤(共75分).
16.(12分)如图所示,已知正三棱柱ABC-A1B1C1的面对角线A1B⊥B1C,求证B1C⊥C1A.
17.(12分)如图所示,在空间四边形AB ( http: / / www.21cnjy.com )CD中,AB=BC,CD=DA,E、F、G分别为CD、DA和AC的中点.求证:平面BEF⊥平面BGD.
18.(12分)如图所示, ( http: / / www.21cnjy.com )△ABC为正三角形,CE⊥平面ABC,BD∥CE,且CE=AC=2BD,M是AE的中点.(1)求证:DE=DA;(2)求证:平面BDM⊥平面ECA;(3)求证:平面DEA⊥平面ECA.
19.(12分)如图,在直四棱柱ABC ( http: / / www.21cnjy.com )D-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1分别是棱AD、AA1的中点.(1)设F是棱AB的中点,证明:直线EE1∥平面FCC1;
(2)证明:平面D1AC⊥平面BB1C1C.
20.(13分)如图,在四棱锥P ( http: / / www.21cnjy.com )ABCD中,底面ABCD是边长为a的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD边的中点.(1)求证:BG⊥平面PAD;(2)求证:AD⊥PB;(3)若E为BC边的中点,能否在棱PC上找一点F,使得平面DEF⊥平面ABCD,并证明你的结论.
21.(14分)如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥ DG,EF∥DG,且AB=AD=DE=DG=2,AC=EF=1.(1)求证:BF∥平面ACGD;(2)求二面角A EG D的正切值.
北师大版必修2第一章《垂直关系》单元测试题答案
一、选择题:
1.[答案] D[解析] 当两点所在直线垂直于平面时,可作无数个;否则,有且仅有1个.
2.[答案] A[解析] 思路解析:∵PA⊥平面ABCD, ∴PA⊥BC.又
∵BC⊥AB,PA∩AB=A,∴PC⊥平面PAB,从而平面PBC⊥平面PAB.
由AD⊥PA,AD⊥AB,PA∩AB=A得AD⊥平面PAB.
∵AD平面PAD,∴平面PAD⊥平面PAB.
3. [答案] C [解析] 折叠后BD=DC=,且∠BDC为二面角的平面角, ∠BDC=90°, ∴BC=.取BC中点E,连结DE,则DE⊥BC,进一步易证AE⊥BC,AE的长为所求距离.
∵AD=,DE=BC=,∴AE=.
4.[答案]A 解析:思路解析:∵PA⊥平面ABCD, ∴PA⊥BC.又
∵BC⊥AB,PA∩AB=A,∴PC⊥平面PAB,从而平面PBC⊥平面PAB.
由AD⊥PA,AD⊥AB,PA∩AB=A得AD⊥平面PAB.
∵AD平面PAD,∴平面PAD⊥平面PAB.
5.[答案] D[解析] A不正确,若点P和直线a确定平面,当b∥时,满足条件的直线不存在;B不正确,若存在,则有a∥b,这与a、b是异面直线矛盾;C不正确,只有a、b垂直时,才能作出满足条件的平面.只有D正确.
6. [答案] C [解析] 由面面平行的判定定理,知②错误;由线面垂直的判定定理知④错误.
7.[答案] B[解析] 若a与b异面时,A、C错;当a与b不垂直时,D错,故选B.
8.[答案] D[解析] 如图所示,∵E、F、G、H分别为AB、BC、CD、DA的中点,∴EFAC,HGAC,∴四边形EFGH是平行四边形,又EH=BD,BD=AC,∴EH=EF,∴四边形EFGH是菱形.取BD中点M,连结AM、CM,∵AB=AD, ∴AM⊥BD,
又CB=CD,∴CM⊥BD,
又AM∩CM=M,∴BD⊥平面ACM,∴BD⊥AC.
又EF∥AC,BD∥EH,∴EF⊥EH,∴四边形EFGH是正方形.
9.[答案] D[解析] 本小题主要考查线面垂直、面面垂直、线线平行和线面平行.点C若在内,则有AC⊥,若不在内,则AC不垂直于,这是面面垂直的性质,故选D.
10.[答案] B[解析] 可以墙角为例知A错;B中,由⊥,由内有直线b⊥,而∥,则内有a∥b,则a⊥,⊥.
二、填空题:
11. [答案] MN⊥AB[解析] 如图所示,由长方体的性质知,平面BCC1B1⊥平面ABCD,交线为BC.
∵MN在平面BCC1B1内,且MN⊥BC,
∴MN⊥平面ABCD,而AB 平面ABCD,
∴MN⊥AB.
12.[答案] ②③④ ①(答案不惟一)
13.[答案] BM⊥PC(其它合理即可)
[解析]∵四边形ABCD的边长相等,
∴四边形为菱形.∴AC⊥BD,
又∵PA⊥面ABCD,∴PA⊥BD,∴BD⊥面PAC,∴BD⊥PC.
若PC⊥面BMD,则PC垂直于面BMD中两条相交直线.
∴当BM⊥PC时,PC⊥面BDM.∴面PCD⊥面BDM.
14. [答案]①④⑤ [解析] ( http: / / www.21cnjy.com ) ①④易判断,⑤中△PMN是正三角形且AM=AP=AN,因此,三棱锥A-PMN是正三棱锥,所以图⑤中l⊥平面MNP,由此法还可否定③.∵AM≠AP≠AN,也易否定②.
15.[答案]直线 [解析] 过点A与AB垂直的所有直线都在同一个平面内,∵AB是的斜线,∴与不平行.从而与的所有公共点都在同一条直线上,即与的交线上.从而内所有过点A与相交的直线,其交点都在此交线上.
三、解答题:
16.[解析] 如图所示,连结A1C,交AC1于点D,则点D是A1C的中点.
取BC的中点N,连结AN、DN,则DN∥A1B.
又A1B⊥B1C,∴B1C⊥DN.
又△ABC是正三角形, ∴AN⊥BC.
又平面ABC⊥平面BB1C1C,平面ABCD∩平面BB1C1C=BC,AN 平面ABC,
∴AN⊥平面BB1C1C.又B1C 平面BB1C1C,
∴B1C⊥AN.
又AN 平面AND,DN 平面AND,AN∩DN=N,
∴B1C⊥平面AND.
又C1A 平面AND,∴B1C⊥AC1.
17.[解析] ∵AB=BC,CD=AD,G是AC的中点,
∴BG⊥AC,DG⊥AC.
∴AC⊥平面BGD.又EF∥AC,
∴EF⊥平面BGD.又EF 平面BEF,
∴平面BDG⊥平面BEF.
18.[解析] (1)取EC的中点F,连结DF.
∵CE⊥平面ABC,∴CE⊥BC.
易知DF∥BC,∴CE⊥DF.
∵BD∥CE,∴BD∥平面ABC.
在Rt△EFD和Rt△DBA中,EF=CE=DB,DF=BC=AB,
∴Rt△EFD≌Rt△DBA.故DE=DA.
(2)取AC的中点N,连结MN、BN,则MNCF.
∵BDCF, ∴MNBD, ∴N∈平面BDM.
∵EC⊥平面ABC, ∴EC⊥BN.
又∵AC⊥BN,EC∩AC=C, ∴BN⊥平面ECA.
又∵BN 平面BDM, ∴平面BDM⊥平面ECA.
(3)∵DM∥BN,BN⊥平面ECA, ∴DM⊥平面ECA.
又∵DM 平面DEA,∴平面DEA⊥平面ECA.
19.[解析](1)解法一:取A1B1的中点F1,连结FF1、C1F1,
∵FF1∥BB1∥CC1,∴F1∈平面FCC1,
∴平面FCC1即为平面C1CFF1,
连结A1D、F1C,∴A1F1D1C1CD,
∴四边形A1DCF1为平行四边形,
∴A1D∥F1C.
又∵EE1∥A1D,∴EE1∥F1C,
∵EE1平面FCC1,F1C 平面FCC1,
∴EE1∥平面FCC1.
解法二:∵F为AB的中点,CD=2,AB=4,AB∥CD,
∴CDAF,∴四边形AFCD为平行四边形,∴AD∥FC.
又CC1∥DD1,FC∩CC1=C,FC 平面FCC1,CC1 平面FCC1,
∴平面ADD1A1∥平面FCC1,
又EE1 平面ADD1A1,∴EE1∥平面FCC1.
(2)证明:连结AC,在△FBC中,FC=BC=FB,
又F为AB的中点,∴AF=FC=FB,
∴∠ACB=90°,即AC⊥BC.
又AC⊥CC1,且CC1∩BC=C,
∴AC⊥平面BB1C1C,而AC 平面D1AC;
故平面D1AC⊥平面BB1C1C.
20.(1)证明:∵在菱形ABCD中,∠DAB=60°,G为AD边的中点,
∴BG⊥AD.
又∵平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD.
(2)证明:连接PG,则PG⊥AD,
由(1)得BG⊥AD,
又∵PG∩BG=G,BG平面PBG,
PG平面PBG,
∴AD⊥平面PBG.
∵PB平面PBG,∴AD⊥PB.
(3)解:当F为PC的中点时,满足平面DEF⊥平面ABCD.
证明如下:
取PC的中点F,连接DE,EF,DF,则由平面几何知识,
在△PBC中,EF∥PB,
在菱形ABCD中,GB∥DE,
而EF平面DEF,ED平面DEF,
EF∩DE=E,
PB平面PGB,GB平面PGB,
PB∩GB=B,
∴平面DEF∥平面PGB.
又∵侧面PAD为正三角形,G为AD的中点,∴PG⊥AD.
又∵侧面PAD所在平面垂直于底面ABCD,
∴PG⊥平面ABCD,而PG平面PGB,
∴平面PGB⊥平面ABCD.
故平面DEF⊥平面ABCD.
21.(1)证明:设DG的中点为M,连接AM,FM,则由已知条件易证四边形DEFM是平行四边形,
∴MF∥DE,且MF=DE.
∵平面ABC∥平面DEFG,平面ABED分别交平面ABC,平面DEFG于AB,DE,∴AB∥DE,又AB=DE,
∴MF∥AB,且MF=AB,
∴四边形ABFM是平行四边形,即BF∥AM.又BF平面ACGD,AM平面ACGD,故BF∥平面ACGD.
(2)解:连接AE,AG,EG,
∵AD⊥平面DEFG,
∴AD⊥DG,AD⊥DE.
∵AD=ED=DG,∴AE=AG.
取EG的中点H,连接AH,DH,有AH⊥EG,DH⊥EG,
则∠AHD是二面角A EG D的平面角.
∵在Rt△ADH中,由AD=DE=DG=2,得DH=.
∴tan∠AHD==,
故二面角A EG D的正切值为.
