江西省吉安三中高中数学北师大版必修2第一章《空间图形的基本关系与公理》单元测试
文档属性
| 名称 | 江西省吉安三中高中数学北师大版必修2第一章《空间图形的基本关系与公理》单元测试 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-17 00:00:00 | ||
图片预览

文档简介
北师大版必修2第一章《空间图形的基本关系与公理》
单元测试题
班级: 姓名:
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.下列命题中,正确命题的个数为( )
①平面的基本性质1可用集合符号叙述为:若A∈,B∈,且A∈,B∈,则必有∈;
②四边形的两条对角线必相交于一点;
③用平行四边形表示的平面,以平行四边形的四条边作为平面的边界线;
④平行四边形是平面图形.
A.1个 B.2个 C.3个 D.4个
2.若三条直线两两相交,则由这三条直线所确定的平面的个数是( )
A.1个 B.2个 C.3个 D.1个或3个
3.已知空间四点A、B、C、D确定惟一一个平面,那么这四个点中( )
A.必定只有三点共线 B.必有三点不共线
C.至少有三点共线 D.不可能有三点共线
4.有两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形( )
A.全等 B.相似 C.有一个角相等 D.全等或相似
5.分别和两条异面直线都相交的两条直线的位置关系是( )
A.异面 B.相交 C.平行 D.异面或相交
6.如图所示,设E、F、G、H依次是空间 ( http: / / www.21cnjy.com )四边形ABCD边AB、BC、CD、DA上除端点外的点,==λ,==μ,则下列结论中不正确的为( )
A.当λ=μ时,四边形EFGH是平行四边形
B.当λ≠μ时,四边形EFGH是梯形
C.当λ≠μ时,四边形EFGH一定不是平行四边形
D.当λ=μ时,四边形EFGH是梯形
7.a、b、c是三条直线,若a与b异面,b与c异面,则a与c的位置关系( )
A.异面 B.平行 C.相交 D.都有可能
8.在空间中有下列四个命题:①有两组对边相 ( http: / / www.21cnjy.com )等的四边形是平行四边形;②四边相等的四边形是菱形;③两组对边分别平行的四边形是平行四边形;④连接空间四边形各边中点的四边形一定是梯形.其中正确命题的个数为( )
A.1 B.2 C.3 D.4
9.已知a、b是异面直线,直线c平行于直线a,那么c与b( )
A.一定是异面直线 B.一定是相交直线
C.不可能是平行直线 D.不可能是相交直线
10.下列说法中正确的是( )
A.空间中没有交点的两条直线是平行直线
B.一条直线和两条平行直线中的一条相交,则它和另一条也相交
C.空间四条直线a、b、c、d,如果a∥b,c∥d,且a∥d,那么b∥c
D.分别在两个平面内的直线是平行直线
二、填空题:请把答案填在题中横线上(每小题5分,共25分).
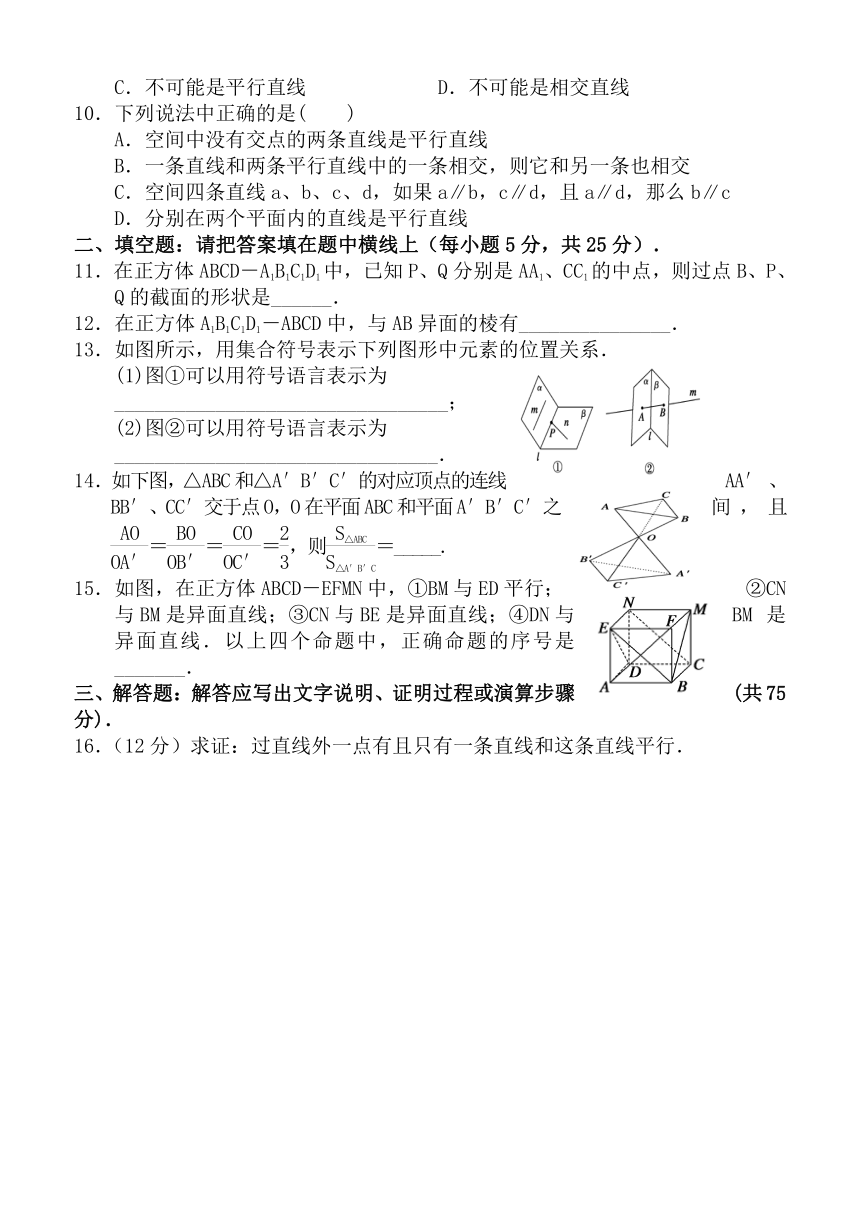
11.在正方体ABCD-A1B1C1D1中,已知P、Q分别是AA1、CC1的中点,则过点B、P、Q的截面的形状是______.
12.在正方体A1B1C1D1-ABCD中,与AB异面的棱有_______________.
13.如图所示,用集合符号表示下列图形中元素的位置关系.
(1)图①可以用符号语言表示为
_________________________________;
(2)图②可以用符号语言表示为
________________________________.
14.如下图,△ABC和△A′B′C′的对 ( http: / / www.21cnjy.com )应顶点的连线AA′、BB′、CC′交于点O,O在平面ABC和平面A′B′C′之间,且===,则=_____.
15.如图,在正方体ABC ( http: / / www.21cnjy.com )D-EFMN中,①BM与ED平行;②CN与BM是异面直线;③CN与BE是异面直线;④DN与BM是异面直线.以上四个命题中,正确命题的序号是_______.
三、解答题:解答应写出文字说明、证明过程或演算步骤(共75分).
16.(12分)求证:过直线外一点有且只有一条直线和这条直线平行.
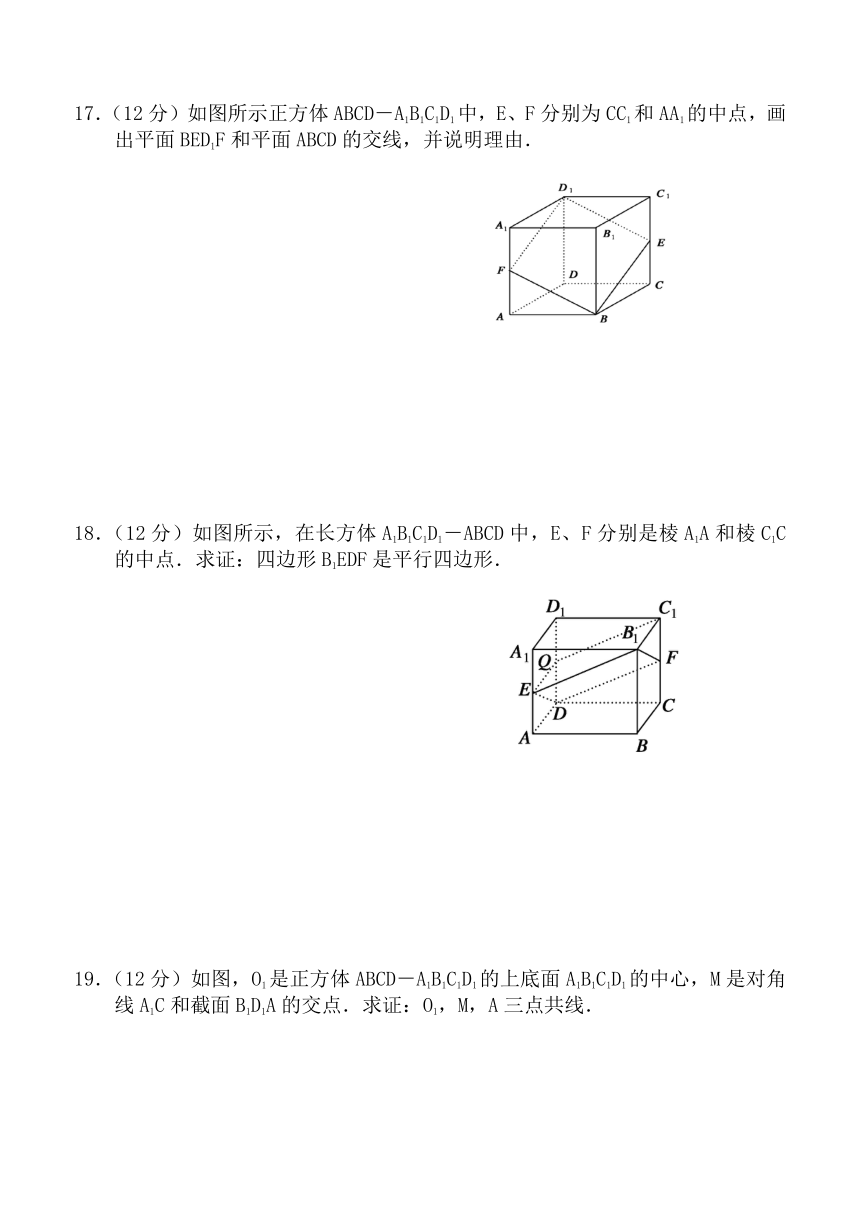
17.(12分)如图所示正方体ABCD ( http: / / www.21cnjy.com )-A1B1C1D1中,E、F分别为CC1和AA1的中点,画出平面BED1F和平面ABCD的交线,并说明理由.
18.(12分)如图所示,在长方体A1B1C1D1-ABCD中,E、F分别是棱A1A和棱C1C的中点.求证:四边形B1EDF是平行四边形.
19.(12分)如图,O1是正方体ABCD-A1B1C1D1的上底面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点.求证:O1,M,A三点共线.
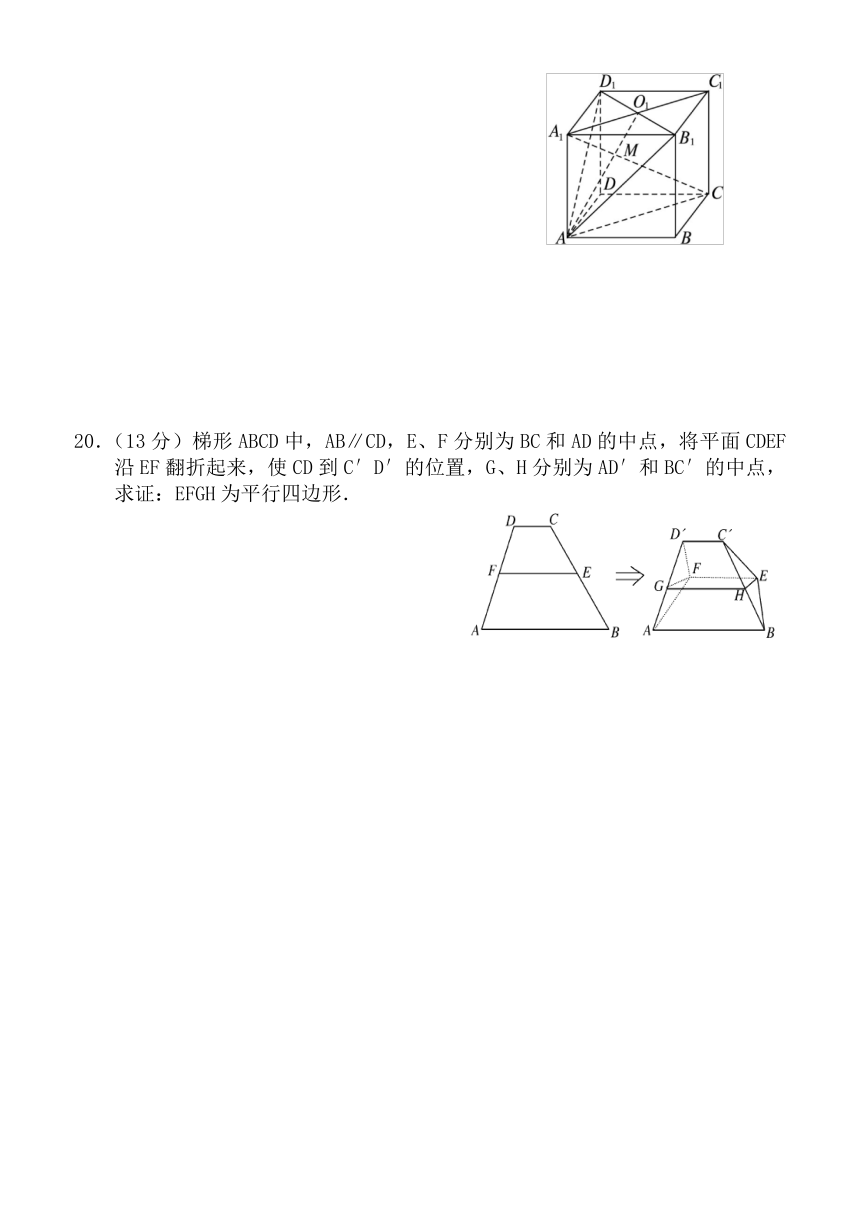
20.(13分)梯形ABCD中,A ( http: / / www.21cnjy.com )B∥CD,E、F分别为BC和AD的中点,将平面CDEF沿EF翻折起来,使CD到C′D′的位置,G、H分别为AD′和BC′的中点,求证:EFGH为平行四边形.
( http: / / www.21cnjy.com )
21.(14分)如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;(2)求证:∠BMC=∠B1M1C1.
北师大版必修2第一章《空间图形的基本关系与公理》
单元测试题答案
一、选择题:
1.[答案]A[解析] ①中,l∈ ( http: / / www.21cnjy.com )α不对,应为l α;②中,当四边形的四个顶点不共面时,两条对角线不能相交;③中,平面是无限延展的,用平行四边形表示平面,平行四边形的边并不表示平面的边界线;④平行四边形是平面图形(原理:两条平行直线确定一个平面),故只有④正确.
2.[答案]D[解析] 如图(1)所示的三条两两相交直线确定一个平面;如图(2)所示的三条两两相交直线确定三个平面.
3.[答案]B[解析] 四点A、B、C、D确 ( http: / / www.21cnjy.com )定惟一一个平面,则AB与CD相交或平行,AB∥CD时,选项A、C错,AB与CD相交于点A时,D错.
4.[答案]D
5.[答案]D[解析]a,b为异面直线,c,d分别与a,b都相交.图(1)中c,d异面,图(2)中c,d相交.
6.[答案]D[解析] 由 ( http: / / www.21cnjy.com )==λ,得EH∥BD,且=λ,同理得FG∥BD且=μ,当λ=μ时,EF綊FG.当λ≠μ时,EF∥FG,但EH≠FG,故A、B、C都对,只有D错误.
7.[答案]D[解析] 直线a与c的位置关系有以下三种情形(如下图):
( http: / / www.21cnjy.com )
∴直线a与c的位置关系可能平行(如图(1));可能相交(如图(2));可能异面(如图(3)),故选D.
8. [答案] A[解析 ( http: / / www.21cnjy.com )] 四边相等或两组对边相等的四边形可以是空间四边形,故①②错误,连接空间四边形的各边中点构成的四边形是平行四边形,故④错,易知③对,由此选A.
9.[答案]C[解析] 如图所示,图(1)中,b与c相交,图(2)中b与c异面,假如b∥c,∵a∥c,∴a∥b这与a,b异面矛盾,
∴b与c不可能为平行直线.
10.[答案]C[解析] A、B中,两直线可能异面,D中两直线可能相交,也可能异面.
二、填空题:
11.[答案]菱形 [解析] 先证截面BPD1Q是平行四边形,再证是菱形.
12.[答案]A1D1、DD1、CC1、C1B1
13.[答案] (1)∩=, , ,∩=P,m∥
(2) ∩=,∩=A,∩=B
14.[答案][解析] 由题设条件知===,
∴△ABC∽△A′B′C′.∴=.
15.[答案] ②④[解析] 观察图形 ( http: / / www.21cnjy.com ),根据异面直线的定义可知,BM与ED是异面直线,CN与BM是异面直线,CN与BE不是异面直线,DN与BM是异面直线,故①、③错误,②、④正确.即正确命题的序号是②、④.
三、解答题
16.已知:点P 直线a.求证:过点P和直线a平行的直线b有且只有一条.
[解析] ∵P a,∴点P和直线a确定一个平面α,在平面α内过点P作直线b与直线a平行(由平面几何知识),故存在.
假设过点P,还有一条直线c与a平行.
∵a∥ b,a∥c,
∴b∥c,这与b、c共点P矛盾,故假设不成立,因此直线b惟一.
即过直线外一点有且只有一条直线和这条直线平行.
17.[解析] 如图所示,在平面ADD1A1内延长D1F与DA,交于一点P,则P∈平面BED1F,
∵DA 平面ABCD,∴P∈平面ABCD,
∴P是平面ABCD与平面BED1F的一个公共点,
又B是两平面的一个公共点,
∴PB为两平面的交线.
18.[解析] 设Q是D1D的中点,连结EQ、QC1,
∵E是A1A的中点,∴EQA1D1.
在矩形A1B1C1D1中,有A1D1B1C1.
由基本性质4,得EQ//B1C1.
∴四边形EQC1B1是平行四边形.∴B1E//C1Q.
又由F、Q分别是矩形C1CDD1中CC1、D1D两边的中点.得QD//C1F.
∴四边形DQC1F是平行四边形,从而C1QFD.
由基本性质4,得B1EFD,
所以四边形B1EDF是平行四边形.
19.证明:因为上底面中A1C1∩B1D1=O1,A1C1平面A1C1CA,B1D1平面AB1D1,所以,O1是平面A1C1CA与平面AB1D1的公共点.
又因为A1C∩平面AB1D1=M,A1C平面A1C1CA,
所以,M是平面A1C1CA与平面AB1D1的公共点.
又因为A∈平面AB1D1,A∈平面A1C1CA,
所以,A是平面A1C1CA与平面AB1D1的公共点.
所以,O1,M,A都是平面A1C1CA与平面AB1D1的公共点,由公理3可知,O1,M,A三点共线.
20.[解析] ∵梯形ABCD中,AB∥CD,
E、F分别为BC、AD的中点,
∴EF∥AB且EF=(AB+CD),
又C′D′∥EF,EF∥AB,∴C′D′∥AB.
∵G、H分别为AD′、BC′的中点,
( http: / / www.21cnjy.com )
∴GH∥AB且GH=(AB+C′D′)=(AB+CD),
∴GH綊EF,∴EFGH为平行四边形.
21.证明:(1)在正方形ADD1A1中,M,M1分别为AD,A1D1的中点,
∴MM1=AA1,MM1∥AA1.
又∵AA1=BB1,AA1∥BB1,
∴MM1∥BB1,且MM1=BB1,
∴四边形BB1M1M为平行四边形.
(2)方法一:由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角,
∴∠BMC=∠B1M1C1.
方法二:由(1)知四边形BB1M1M为平行四边形,
∴B1M1=BM.
同理可得四边形CC1M1M为平行四边形.
∴C1M1=CM.
又∵B1C1=BC,∴△BCM≌△B1C1M1.
∴∠BMC=∠B1M1C1.
单元测试题
班级: 姓名:
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.下列命题中,正确命题的个数为( )
①平面的基本性质1可用集合符号叙述为:若A∈,B∈,且A∈,B∈,则必有∈;
②四边形的两条对角线必相交于一点;
③用平行四边形表示的平面,以平行四边形的四条边作为平面的边界线;
④平行四边形是平面图形.
A.1个 B.2个 C.3个 D.4个
2.若三条直线两两相交,则由这三条直线所确定的平面的个数是( )
A.1个 B.2个 C.3个 D.1个或3个
3.已知空间四点A、B、C、D确定惟一一个平面,那么这四个点中( )
A.必定只有三点共线 B.必有三点不共线
C.至少有三点共线 D.不可能有三点共线
4.有两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形( )
A.全等 B.相似 C.有一个角相等 D.全等或相似
5.分别和两条异面直线都相交的两条直线的位置关系是( )
A.异面 B.相交 C.平行 D.异面或相交
6.如图所示,设E、F、G、H依次是空间 ( http: / / www.21cnjy.com )四边形ABCD边AB、BC、CD、DA上除端点外的点,==λ,==μ,则下列结论中不正确的为( )
A.当λ=μ时,四边形EFGH是平行四边形
B.当λ≠μ时,四边形EFGH是梯形
C.当λ≠μ时,四边形EFGH一定不是平行四边形
D.当λ=μ时,四边形EFGH是梯形
7.a、b、c是三条直线,若a与b异面,b与c异面,则a与c的位置关系( )
A.异面 B.平行 C.相交 D.都有可能
8.在空间中有下列四个命题:①有两组对边相 ( http: / / www.21cnjy.com )等的四边形是平行四边形;②四边相等的四边形是菱形;③两组对边分别平行的四边形是平行四边形;④连接空间四边形各边中点的四边形一定是梯形.其中正确命题的个数为( )
A.1 B.2 C.3 D.4
9.已知a、b是异面直线,直线c平行于直线a,那么c与b( )
A.一定是异面直线 B.一定是相交直线
C.不可能是平行直线 D.不可能是相交直线
10.下列说法中正确的是( )
A.空间中没有交点的两条直线是平行直线
B.一条直线和两条平行直线中的一条相交,则它和另一条也相交
C.空间四条直线a、b、c、d,如果a∥b,c∥d,且a∥d,那么b∥c
D.分别在两个平面内的直线是平行直线
二、填空题:请把答案填在题中横线上(每小题5分,共25分).
11.在正方体ABCD-A1B1C1D1中,已知P、Q分别是AA1、CC1的中点,则过点B、P、Q的截面的形状是______.
12.在正方体A1B1C1D1-ABCD中,与AB异面的棱有_______________.
13.如图所示,用集合符号表示下列图形中元素的位置关系.
(1)图①可以用符号语言表示为
_________________________________;
(2)图②可以用符号语言表示为
________________________________.
14.如下图,△ABC和△A′B′C′的对 ( http: / / www.21cnjy.com )应顶点的连线AA′、BB′、CC′交于点O,O在平面ABC和平面A′B′C′之间,且===,则=_____.
15.如图,在正方体ABC ( http: / / www.21cnjy.com )D-EFMN中,①BM与ED平行;②CN与BM是异面直线;③CN与BE是异面直线;④DN与BM是异面直线.以上四个命题中,正确命题的序号是_______.
三、解答题:解答应写出文字说明、证明过程或演算步骤(共75分).
16.(12分)求证:过直线外一点有且只有一条直线和这条直线平行.
17.(12分)如图所示正方体ABCD ( http: / / www.21cnjy.com )-A1B1C1D1中,E、F分别为CC1和AA1的中点,画出平面BED1F和平面ABCD的交线,并说明理由.
18.(12分)如图所示,在长方体A1B1C1D1-ABCD中,E、F分别是棱A1A和棱C1C的中点.求证:四边形B1EDF是平行四边形.
19.(12分)如图,O1是正方体ABCD-A1B1C1D1的上底面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点.求证:O1,M,A三点共线.
20.(13分)梯形ABCD中,A ( http: / / www.21cnjy.com )B∥CD,E、F分别为BC和AD的中点,将平面CDEF沿EF翻折起来,使CD到C′D′的位置,G、H分别为AD′和BC′的中点,求证:EFGH为平行四边形.
( http: / / www.21cnjy.com )
21.(14分)如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;(2)求证:∠BMC=∠B1M1C1.
北师大版必修2第一章《空间图形的基本关系与公理》
单元测试题答案
一、选择题:
1.[答案]A[解析] ①中,l∈ ( http: / / www.21cnjy.com )α不对,应为l α;②中,当四边形的四个顶点不共面时,两条对角线不能相交;③中,平面是无限延展的,用平行四边形表示平面,平行四边形的边并不表示平面的边界线;④平行四边形是平面图形(原理:两条平行直线确定一个平面),故只有④正确.
2.[答案]D[解析] 如图(1)所示的三条两两相交直线确定一个平面;如图(2)所示的三条两两相交直线确定三个平面.
3.[答案]B[解析] 四点A、B、C、D确 ( http: / / www.21cnjy.com )定惟一一个平面,则AB与CD相交或平行,AB∥CD时,选项A、C错,AB与CD相交于点A时,D错.
4.[答案]D
5.[答案]D[解析]a,b为异面直线,c,d分别与a,b都相交.图(1)中c,d异面,图(2)中c,d相交.
6.[答案]D[解析] 由 ( http: / / www.21cnjy.com )==λ,得EH∥BD,且=λ,同理得FG∥BD且=μ,当λ=μ时,EF綊FG.当λ≠μ时,EF∥FG,但EH≠FG,故A、B、C都对,只有D错误.
7.[答案]D[解析] 直线a与c的位置关系有以下三种情形(如下图):
( http: / / www.21cnjy.com )
∴直线a与c的位置关系可能平行(如图(1));可能相交(如图(2));可能异面(如图(3)),故选D.
8. [答案] A[解析 ( http: / / www.21cnjy.com )] 四边相等或两组对边相等的四边形可以是空间四边形,故①②错误,连接空间四边形的各边中点构成的四边形是平行四边形,故④错,易知③对,由此选A.
9.[答案]C[解析] 如图所示,图(1)中,b与c相交,图(2)中b与c异面,假如b∥c,∵a∥c,∴a∥b这与a,b异面矛盾,
∴b与c不可能为平行直线.
10.[答案]C[解析] A、B中,两直线可能异面,D中两直线可能相交,也可能异面.
二、填空题:
11.[答案]菱形 [解析] 先证截面BPD1Q是平行四边形,再证是菱形.
12.[答案]A1D1、DD1、CC1、C1B1
13.[答案] (1)∩=, , ,∩=P,m∥
(2) ∩=,∩=A,∩=B
14.[答案][解析] 由题设条件知===,
∴△ABC∽△A′B′C′.∴=.
15.[答案] ②④[解析] 观察图形 ( http: / / www.21cnjy.com ),根据异面直线的定义可知,BM与ED是异面直线,CN与BM是异面直线,CN与BE不是异面直线,DN与BM是异面直线,故①、③错误,②、④正确.即正确命题的序号是②、④.
三、解答题
16.已知:点P 直线a.求证:过点P和直线a平行的直线b有且只有一条.
[解析] ∵P a,∴点P和直线a确定一个平面α,在平面α内过点P作直线b与直线a平行(由平面几何知识),故存在.
假设过点P,还有一条直线c与a平行.
∵a∥ b,a∥c,
∴b∥c,这与b、c共点P矛盾,故假设不成立,因此直线b惟一.
即过直线外一点有且只有一条直线和这条直线平行.
17.[解析] 如图所示,在平面ADD1A1内延长D1F与DA,交于一点P,则P∈平面BED1F,
∵DA 平面ABCD,∴P∈平面ABCD,
∴P是平面ABCD与平面BED1F的一个公共点,
又B是两平面的一个公共点,
∴PB为两平面的交线.
18.[解析] 设Q是D1D的中点,连结EQ、QC1,
∵E是A1A的中点,∴EQA1D1.
在矩形A1B1C1D1中,有A1D1B1C1.
由基本性质4,得EQ//B1C1.
∴四边形EQC1B1是平行四边形.∴B1E//C1Q.
又由F、Q分别是矩形C1CDD1中CC1、D1D两边的中点.得QD//C1F.
∴四边形DQC1F是平行四边形,从而C1QFD.
由基本性质4,得B1EFD,
所以四边形B1EDF是平行四边形.
19.证明:因为上底面中A1C1∩B1D1=O1,A1C1平面A1C1CA,B1D1平面AB1D1,所以,O1是平面A1C1CA与平面AB1D1的公共点.
又因为A1C∩平面AB1D1=M,A1C平面A1C1CA,
所以,M是平面A1C1CA与平面AB1D1的公共点.
又因为A∈平面AB1D1,A∈平面A1C1CA,
所以,A是平面A1C1CA与平面AB1D1的公共点.
所以,O1,M,A都是平面A1C1CA与平面AB1D1的公共点,由公理3可知,O1,M,A三点共线.
20.[解析] ∵梯形ABCD中,AB∥CD,
E、F分别为BC、AD的中点,
∴EF∥AB且EF=(AB+CD),
又C′D′∥EF,EF∥AB,∴C′D′∥AB.
∵G、H分别为AD′、BC′的中点,
( http: / / www.21cnjy.com )
∴GH∥AB且GH=(AB+C′D′)=(AB+CD),
∴GH綊EF,∴EFGH为平行四边形.
21.证明:(1)在正方形ADD1A1中,M,M1分别为AD,A1D1的中点,
∴MM1=AA1,MM1∥AA1.
又∵AA1=BB1,AA1∥BB1,
∴MM1∥BB1,且MM1=BB1,
∴四边形BB1M1M为平行四边形.
(2)方法一:由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角,
∴∠BMC=∠B1M1C1.
方法二:由(1)知四边形BB1M1M为平行四边形,
∴B1M1=BM.
同理可得四边形CC1M1M为平行四边形.
∴C1M1=CM.
又∵B1C1=BC,∴△BCM≌△B1C1M1.
∴∠BMC=∠B1M1C1.
