江西省吉安三中高中数学北师大版必修2第一章《直观图》单元测试题
文档属性
| 名称 | 江西省吉安三中高中数学北师大版必修2第一章《直观图》单元测试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-17 00:00:00 | ||
图片预览



文档简介
北师大版必修2第一章《直观图》单元测试题
班级: 姓名:
一、选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.关于斜二测画法画直观图说法不正确的是 ( )
A.在实物图中取坐标系不同,所得的直观图有可能不同
B.平行于坐标轴的线段在直观图中仍然平行于坐标轴
C.平行于坐标轴的线段长度在直观图中仍然保持不变
D.斜二测坐标系取的角可能是135°
2.下列说法正确的是( )
A.互相垂直的两条直线的直观图一定是互相垂直的两条直线
B.梯形的直观图可能是平行四边形
C.矩形的直观图可能是梯形
D.正方形的直观图可能是平行四边形3.如右图所示,该直观图表示的平面图形为( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.正三角形
4.下列几种说法正确的个数是( )
①相等的角在直观图中对应的角仍然相等
②相等的线段在直观图中对应的线段仍然相等
③平行的线段在直观图中对应的线段仍然平行
④线段的中点在直观图中仍然是线段的中点
A.1 B.2 C.3 D.4
5.一个三角形在其直观图中对应一个边长为1正三角形,原三角形的面积为 ( )
A. B. C. D.
6.水平放置的矩形ABCD长AB=4,宽BC=2,以AB、AD为轴作出斜二测直观图A′B′C′D′,则四边形A′B′C′D′的面积为( )
A.4 B.2 C.4 D.2
7.如图,正方形O′A′B′C′的边长为a cm(a>0),它是一个水平放置的平面图形的直观图,则它的原图形OABC的周长是( )
A.8a cm B.6a cm
C.(2a+2a) cm D.4a cm
8.已知正△ABC的边长为a,以它的一边为x轴,对应的高线为y轴,画出它的水平放置的直观图△A′B′C′,则△A′B′C′的面积是( )
A.a2 B.a2 C.a2 D.a2
9.一个建筑物上部为四棱锥,下部为长方体 ( http: / / www.21cnjy.com ),且四棱锥的底面与长方体的上底面尺寸一样,已知长方体的长、宽、高分别为20m,5m,10m,四棱锥的高为8m,若按1:500的比例画出它的直观图,那么直观图中,长方体的长、宽、高和四棱锥的高应分别为( )
A.4cm,1cm,2cm,1.6cm B.4cm,0.5cm,2cm,0.8cm
C.4cm,0.5cm,2cm,1.6cm D.2cm,0.5cm,1cm,0.8cm
10.如图所示是水平放置的三角形的直观图,A′B′∥y′轴,则原图形中△ABC是( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰直角三角形
二、填空题: 请把答案填在题中横线上(每小题5分,共25分).
11.利用斜二测画法得到的:①三角形的直观 ( http: / / www.21cnjy.com )图一定是三角形;②正方形的直观图一定是菱形;③等腰梯形的直观图可以是平行四边形;④菱形的直观图一定是菱形.以上结论正确的个数是________.
12.一个平面四边形的斜二测画法的直观图是一个边长为a的正方形,则原平面四边形的面积等于 .
13. 如图所示的是水平放置的三角形ABC ( http: / / www.21cnjy.com )在直角坐标系中的直观图,其中D′是A′C′的中点,且∠A′C′B′≠30°,则原图形中与线段BD的长相等的线段有________条.
14.水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为________.
15.在棱长为1的正方体AC1中,对角线AC1在六个面上的投影长度总和是________.
三、解答题: 解答应写出文字说明、证明过程或演算步骤(共75分).
16.(12分)如图所示的平行四边形A′B′C′D′是一个平面图形的直观图,且∠D′A′B′=45°,请画出它的实际图形.
17.(12分)画出一个正三棱台的直观图(尺寸:上、下底面边长分别为1 cm,2 cm,高为2 cm).
18.(12分)如图为某一 ( http: / / www.21cnjy.com )几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.
(1)沿图中虚线将它们折叠起来,使P、Q、R、S四点重合,请画出其直观图.
(2)试问需要几个这样的几何体才能拼成一个棱长为6的正方体ABCD-A1B1C1D1?
19.(12分)如图,等腰直角三角形△O′A′B′是△AOB的直观图,∠B′=90°,它的斜边长为O′A′=a,求△AOB的面积.
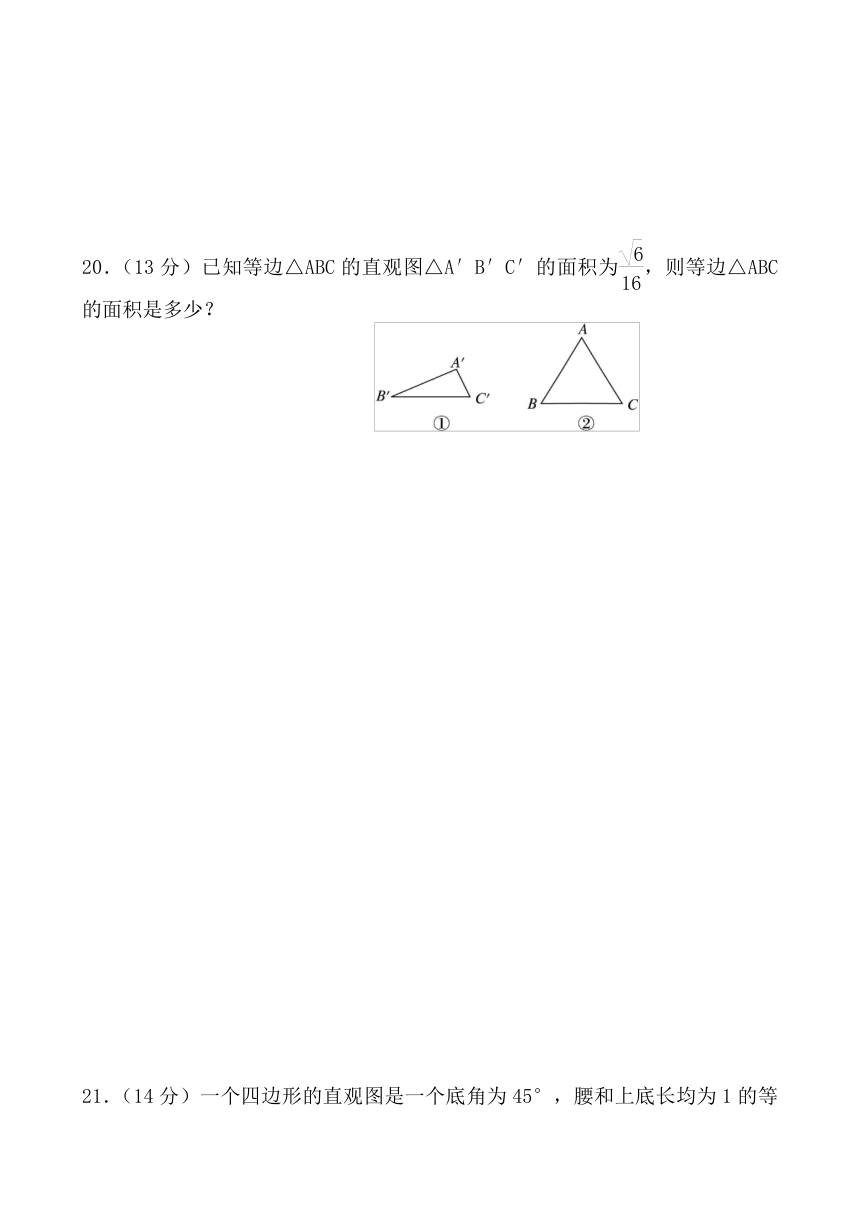
20.(13分)已知等边△ABC的直观图△A′B′C′的面积为,则等边△ABC的面积是多少?
21.(14分)一个四边形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,求原四边形的面积.
① ②
北师大版必修2第一章《直观图》单元测试题答案
一、选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.[答案]C
2.[答案]D3.[答案]C
4.[答案]B
5.[答案]A
6.[答案]B[解析] 平行线在斜二测 ( http: / / www.21cnjy.com )直观图中仍为平行线,∴四边形A′B′C′D′为平行四边形,∠D′A′B′=45°,A′B′=4, A′D′=×2=1,∴D′E=1×sin45°=,
∴S四边形A′B′C′D′=A′B′·D′E=4×=2.
7.[答案]A[解析] 由斜二测画 ( http: / / www.21cnjy.com )法的规则可知,在原图形中OB=2a,OA=a,且OA⊥OB,∴AB=3a,∴OABC的周长为2(a+3a)=8a cm.
8.[答案]D[解析] 如图为△ABC及其直观图A′B′C′.
则有A′B′=AB=a,O′C′=OC=·a=a,∠B′O′C′=45°,
∴S△A′B′C′=A′B′·O′C′·sin45°
=a×a×=a2,故选D.
9.[答案]C[解析] 由比例尺可 ( http: / / www.21cnjy.com )知,长方体的长、宽、高和四棱锥的高应分别为4cm,1cm,2cm和1.6cm,再结合直观图,图形的尺寸应为4cm,0.5cm,2cm,1.6cm.
10.[答案] C[解析] 本题主要考查由直 ( http: / / www.21cnjy.com )观图还原为原图,将斜二测画法逆用,即与x′O′y′坐标轴平行的线与xOy系中坐标轴垂直,且AB=2A′B′,AC=A′C′.如图,故选C.
二、填空题: 请把答案填在题中横线上(每小题5分,共25分).
11.答案:1解析:由斜二 ( http: / / www.21cnjy.com )测画法的规则可知①正确;②错误,是一般的平行四边形;③错误,等腰梯形的直观图不可能是平行四边形;而菱形的直观图也不一定是菱形,④也错误.
12.[答案] 2a2 解析:根据斜二测画法画平面图形的直观图的规则,可以得出一个平面图形的面积S与它的直观图的面积S′之间的关系是S′=S,本题中直观图的面积为a2,所以原平面四边形的面积等于=2a2.
13. [答案]2[解析] △ABC为直角三角形,由D为AC中点,∴BD =AD=CD.∴与BD的长相等的线段有两条.
14.[答案][解析] 原图中AC=3,BC=4,且△ABC为直角三角形,故斜边上的中线长为=.
15.[答案] 6[解析]AC1在六个面上的投影均为每个面的对角线,因此投影长度总和是6.
三、解答题: 解答应写出文字说明、证明过程或演算步骤(共75分).
16.[解析] ①在直观图A′B′C′中建立坐标系x′A′y′,再建立一个直角坐标系xOy,如图所示.
②在x轴上截取线段AB=A′B′,在y轴上截取线段AD,使AD=2A′D′.
③过B作BC∥AD,过D作DC∥AB,使BC与DC交于点C,则四边形ABCD为四边形A′B′C′D′的实际图形.
17.思路分析:先画出上、下底面(正三角形)的直观图,再画出整个正三棱台的直观图.
解:(1)画轴,以底面△ABC的中心O为原点,OC所在直线为y轴,平行于AB的直线为x 轴,使∠xOy=45°,垂直于x轴的直线为z轴.
(2)画下底面,在xOy平面上画△ABC的直观图,在y轴上量取OC= cm,OD= cm.
过D作AB∥x轴,AB=2 cm,且以D为中点,连接AC,BC,则△ABC为下底面三角形的直观图.
(3)画上底面,在z轴上截取OO′=2 cm,
过O′作x′轴∥x轴,y′轴∥y轴,在 ( http: / / www.21cnjy.com )y′轴上量取O′C′= cm,O′D′= cm,过D′作A′B′∥x′轴,A′B′=1 cm,且以D′ 为中点,则△A′B′C′为上底面三角形的直观图.
(4)连线成图,连接AA′,BB′,CC′,并擦去辅助线,则三棱台ABC A′B′C′即为所要画的正三棱台的直观图.
18.解:(1)它是有一条侧棱垂直于底面的四棱锥,其直观图如图,PD=AD=DC=CB=BA=6,PC=PA=6,PB=6
(2)由题意,PD⊥平面ABCD,则VP ABCD=×6×6×6=72,VABCD A1B1C1D1=6×6×6=216,
∵216=72×3
∴需要3个这样的几何体可以拼成一个棱长为6的正方体ABCD-A1B1C1D1
19.[解析]根据斜二测画法的规则,∠AOB=90°,
又△A′O′B′为等腰直角三角形,
∴O′B′=a,
∴OB=2O′B′=a,
∴S△AOB=a·a=a2.
20.解:按照斜二测画法的规则,把如图 ( http: / / www.21cnjy.com )①等边△ABC的直观图△A′B′C′还原为如图②等边△ABC,设AB=x,则B′C′=x,等边△ABC的高为x,
所以△A′B′C′的高为×x=x,
所以△A′B′C′的面积为×x×x=x2=,
解得x=1,
所以△ABC的面积为×x×x=x2=.
21.思路分析:由直观图确定原来的图形的形状及数量关系,关键要把握“横坐标不变,纵坐标减半”的原理,逆推即可.
解:如图①是四边形的直观图,取B′ ( http: / / www.21cnjy.com )C′所在直线为x′轴,因为∠A′B′C′=45°,所以取B′A′所在直线为y′轴,过D′作D′E′∥A′B′,D′E′交B′C′于E′,则B′E′=A′D′=1.
① ②
又因为梯形为等腰梯形,
所以△E′D′C′为等腰直角三角形,
所以E′C′=,所以B′C′=1+.
再建立一个直角坐标系xBy,如图②所示,在x轴上截取线段BC=B′C′=1+,在y轴上截取线段BA=2B′A′=2,过A作AD∥BC,截取AD=A′D′=1,连接CD,则四边形ABCD就是四边形A′B′C′D′的实际图形,四边形ABCD为直角梯形,上底AD=1,下底BC=1+,高AB=2,所以S梯形ABCD=AB·(AD+BC)=×2×(1+1+)=2+.
班级: 姓名:
一、选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.关于斜二测画法画直观图说法不正确的是 ( )
A.在实物图中取坐标系不同,所得的直观图有可能不同
B.平行于坐标轴的线段在直观图中仍然平行于坐标轴
C.平行于坐标轴的线段长度在直观图中仍然保持不变
D.斜二测坐标系取的角可能是135°
2.下列说法正确的是( )
A.互相垂直的两条直线的直观图一定是互相垂直的两条直线
B.梯形的直观图可能是平行四边形
C.矩形的直观图可能是梯形
D.正方形的直观图可能是平行四边形3.如右图所示,该直观图表示的平面图形为( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.正三角形
4.下列几种说法正确的个数是( )
①相等的角在直观图中对应的角仍然相等
②相等的线段在直观图中对应的线段仍然相等
③平行的线段在直观图中对应的线段仍然平行
④线段的中点在直观图中仍然是线段的中点
A.1 B.2 C.3 D.4
5.一个三角形在其直观图中对应一个边长为1正三角形,原三角形的面积为 ( )
A. B. C. D.
6.水平放置的矩形ABCD长AB=4,宽BC=2,以AB、AD为轴作出斜二测直观图A′B′C′D′,则四边形A′B′C′D′的面积为( )
A.4 B.2 C.4 D.2
7.如图,正方形O′A′B′C′的边长为a cm(a>0),它是一个水平放置的平面图形的直观图,则它的原图形OABC的周长是( )
A.8a cm B.6a cm
C.(2a+2a) cm D.4a cm
8.已知正△ABC的边长为a,以它的一边为x轴,对应的高线为y轴,画出它的水平放置的直观图△A′B′C′,则△A′B′C′的面积是( )
A.a2 B.a2 C.a2 D.a2
9.一个建筑物上部为四棱锥,下部为长方体 ( http: / / www.21cnjy.com ),且四棱锥的底面与长方体的上底面尺寸一样,已知长方体的长、宽、高分别为20m,5m,10m,四棱锥的高为8m,若按1:500的比例画出它的直观图,那么直观图中,长方体的长、宽、高和四棱锥的高应分别为( )
A.4cm,1cm,2cm,1.6cm B.4cm,0.5cm,2cm,0.8cm
C.4cm,0.5cm,2cm,1.6cm D.2cm,0.5cm,1cm,0.8cm
10.如图所示是水平放置的三角形的直观图,A′B′∥y′轴,则原图形中△ABC是( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰直角三角形
二、填空题: 请把答案填在题中横线上(每小题5分,共25分).
11.利用斜二测画法得到的:①三角形的直观 ( http: / / www.21cnjy.com )图一定是三角形;②正方形的直观图一定是菱形;③等腰梯形的直观图可以是平行四边形;④菱形的直观图一定是菱形.以上结论正确的个数是________.
12.一个平面四边形的斜二测画法的直观图是一个边长为a的正方形,则原平面四边形的面积等于 .
13. 如图所示的是水平放置的三角形ABC ( http: / / www.21cnjy.com )在直角坐标系中的直观图,其中D′是A′C′的中点,且∠A′C′B′≠30°,则原图形中与线段BD的长相等的线段有________条.
14.水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为________.
15.在棱长为1的正方体AC1中,对角线AC1在六个面上的投影长度总和是________.
三、解答题: 解答应写出文字说明、证明过程或演算步骤(共75分).
16.(12分)如图所示的平行四边形A′B′C′D′是一个平面图形的直观图,且∠D′A′B′=45°,请画出它的实际图形.
17.(12分)画出一个正三棱台的直观图(尺寸:上、下底面边长分别为1 cm,2 cm,高为2 cm).
18.(12分)如图为某一 ( http: / / www.21cnjy.com )几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.
(1)沿图中虚线将它们折叠起来,使P、Q、R、S四点重合,请画出其直观图.
(2)试问需要几个这样的几何体才能拼成一个棱长为6的正方体ABCD-A1B1C1D1?
19.(12分)如图,等腰直角三角形△O′A′B′是△AOB的直观图,∠B′=90°,它的斜边长为O′A′=a,求△AOB的面积.
20.(13分)已知等边△ABC的直观图△A′B′C′的面积为,则等边△ABC的面积是多少?
21.(14分)一个四边形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,求原四边形的面积.
① ②
北师大版必修2第一章《直观图》单元测试题答案
一、选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.[答案]C
2.[答案]D3.[答案]C
4.[答案]B
5.[答案]A
6.[答案]B[解析] 平行线在斜二测 ( http: / / www.21cnjy.com )直观图中仍为平行线,∴四边形A′B′C′D′为平行四边形,∠D′A′B′=45°,A′B′=4, A′D′=×2=1,∴D′E=1×sin45°=,
∴S四边形A′B′C′D′=A′B′·D′E=4×=2.
7.[答案]A[解析] 由斜二测画 ( http: / / www.21cnjy.com )法的规则可知,在原图形中OB=2a,OA=a,且OA⊥OB,∴AB=3a,∴OABC的周长为2(a+3a)=8a cm.
8.[答案]D[解析] 如图为△ABC及其直观图A′B′C′.
则有A′B′=AB=a,O′C′=OC=·a=a,∠B′O′C′=45°,
∴S△A′B′C′=A′B′·O′C′·sin45°
=a×a×=a2,故选D.
9.[答案]C[解析] 由比例尺可 ( http: / / www.21cnjy.com )知,长方体的长、宽、高和四棱锥的高应分别为4cm,1cm,2cm和1.6cm,再结合直观图,图形的尺寸应为4cm,0.5cm,2cm,1.6cm.
10.[答案] C[解析] 本题主要考查由直 ( http: / / www.21cnjy.com )观图还原为原图,将斜二测画法逆用,即与x′O′y′坐标轴平行的线与xOy系中坐标轴垂直,且AB=2A′B′,AC=A′C′.如图,故选C.
二、填空题: 请把答案填在题中横线上(每小题5分,共25分).
11.答案:1解析:由斜二 ( http: / / www.21cnjy.com )测画法的规则可知①正确;②错误,是一般的平行四边形;③错误,等腰梯形的直观图不可能是平行四边形;而菱形的直观图也不一定是菱形,④也错误.
12.[答案] 2a2 解析:根据斜二测画法画平面图形的直观图的规则,可以得出一个平面图形的面积S与它的直观图的面积S′之间的关系是S′=S,本题中直观图的面积为a2,所以原平面四边形的面积等于=2a2.
13. [答案]2[解析] △ABC为直角三角形,由D为AC中点,∴BD =AD=CD.∴与BD的长相等的线段有两条.
14.[答案][解析] 原图中AC=3,BC=4,且△ABC为直角三角形,故斜边上的中线长为=.
15.[答案] 6[解析]AC1在六个面上的投影均为每个面的对角线,因此投影长度总和是6.
三、解答题: 解答应写出文字说明、证明过程或演算步骤(共75分).
16.[解析] ①在直观图A′B′C′中建立坐标系x′A′y′,再建立一个直角坐标系xOy,如图所示.
②在x轴上截取线段AB=A′B′,在y轴上截取线段AD,使AD=2A′D′.
③过B作BC∥AD,过D作DC∥AB,使BC与DC交于点C,则四边形ABCD为四边形A′B′C′D′的实际图形.
17.思路分析:先画出上、下底面(正三角形)的直观图,再画出整个正三棱台的直观图.
解:(1)画轴,以底面△ABC的中心O为原点,OC所在直线为y轴,平行于AB的直线为x 轴,使∠xOy=45°,垂直于x轴的直线为z轴.
(2)画下底面,在xOy平面上画△ABC的直观图,在y轴上量取OC= cm,OD= cm.
过D作AB∥x轴,AB=2 cm,且以D为中点,连接AC,BC,则△ABC为下底面三角形的直观图.
(3)画上底面,在z轴上截取OO′=2 cm,
过O′作x′轴∥x轴,y′轴∥y轴,在 ( http: / / www.21cnjy.com )y′轴上量取O′C′= cm,O′D′= cm,过D′作A′B′∥x′轴,A′B′=1 cm,且以D′ 为中点,则△A′B′C′为上底面三角形的直观图.
(4)连线成图,连接AA′,BB′,CC′,并擦去辅助线,则三棱台ABC A′B′C′即为所要画的正三棱台的直观图.
18.解:(1)它是有一条侧棱垂直于底面的四棱锥,其直观图如图,PD=AD=DC=CB=BA=6,PC=PA=6,PB=6
(2)由题意,PD⊥平面ABCD,则VP ABCD=×6×6×6=72,VABCD A1B1C1D1=6×6×6=216,
∵216=72×3
∴需要3个这样的几何体可以拼成一个棱长为6的正方体ABCD-A1B1C1D1
19.[解析]根据斜二测画法的规则,∠AOB=90°,
又△A′O′B′为等腰直角三角形,
∴O′B′=a,
∴OB=2O′B′=a,
∴S△AOB=a·a=a2.
20.解:按照斜二测画法的规则,把如图 ( http: / / www.21cnjy.com )①等边△ABC的直观图△A′B′C′还原为如图②等边△ABC,设AB=x,则B′C′=x,等边△ABC的高为x,
所以△A′B′C′的高为×x=x,
所以△A′B′C′的面积为×x×x=x2=,
解得x=1,
所以△ABC的面积为×x×x=x2=.
21.思路分析:由直观图确定原来的图形的形状及数量关系,关键要把握“横坐标不变,纵坐标减半”的原理,逆推即可.
解:如图①是四边形的直观图,取B′ ( http: / / www.21cnjy.com )C′所在直线为x′轴,因为∠A′B′C′=45°,所以取B′A′所在直线为y′轴,过D′作D′E′∥A′B′,D′E′交B′C′于E′,则B′E′=A′D′=1.
① ②
又因为梯形为等腰梯形,
所以△E′D′C′为等腰直角三角形,
所以E′C′=,所以B′C′=1+.
再建立一个直角坐标系xBy,如图②所示,在x轴上截取线段BC=B′C′=1+,在y轴上截取线段BA=2B′A′=2,过A作AD∥BC,截取AD=A′D′=1,连接CD,则四边形ABCD就是四边形A′B′C′D′的实际图形,四边形ABCD为直角梯形,上底AD=1,下底BC=1+,高AB=2,所以S梯形ABCD=AB·(AD+BC)=×2×(1+1+)=2+.
