人教版八年级上册第十二章 直角三角形 课件(共22张PPT)
文档属性
| 名称 | 人教版八年级上册第十二章 直角三角形 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 708.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 17:03:39 | ||
图片预览


文档简介
(共22张PPT)
专题三 直角三角形
八 年 级 数 学
内容提要
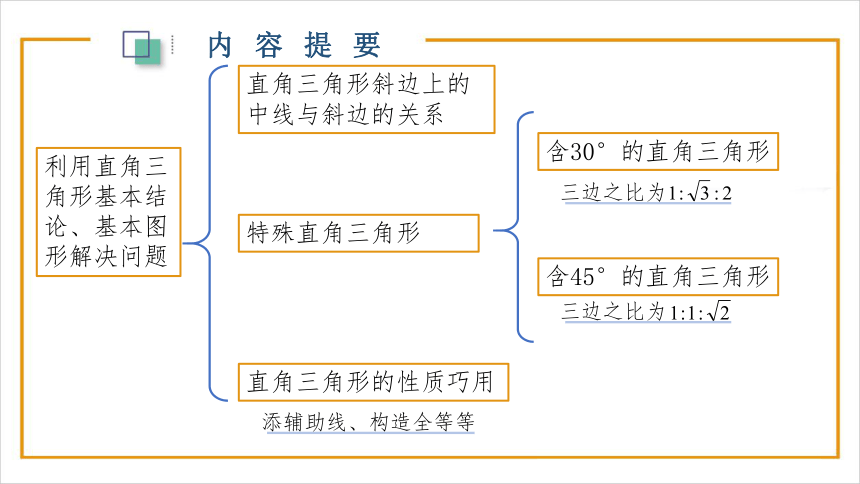
利用直角三角形基本结论、基本图形解决问题
直角三角形斜边上的 中线与斜边的关系
特殊直角三角形
含30°的直角三角形
含45°的直角三角形
三边之比为
三边之比为
直角三角形的性质巧用
添辅助线、构造全等等
课前练习
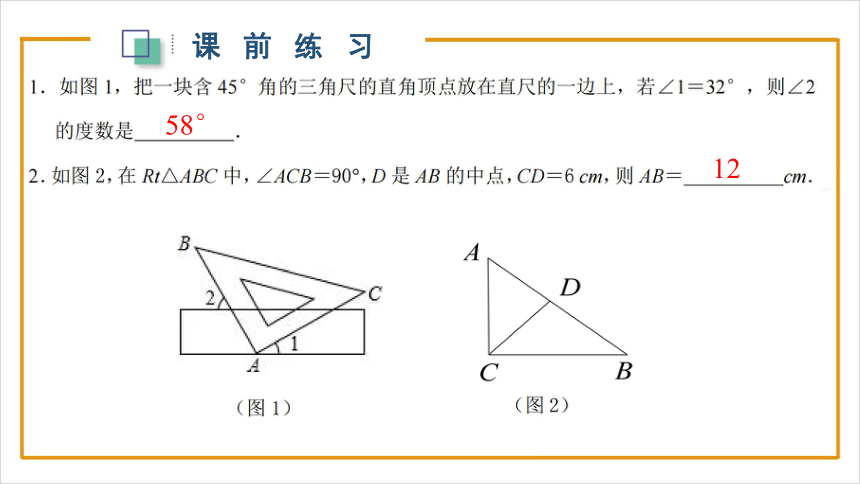
58°
12
课前练习
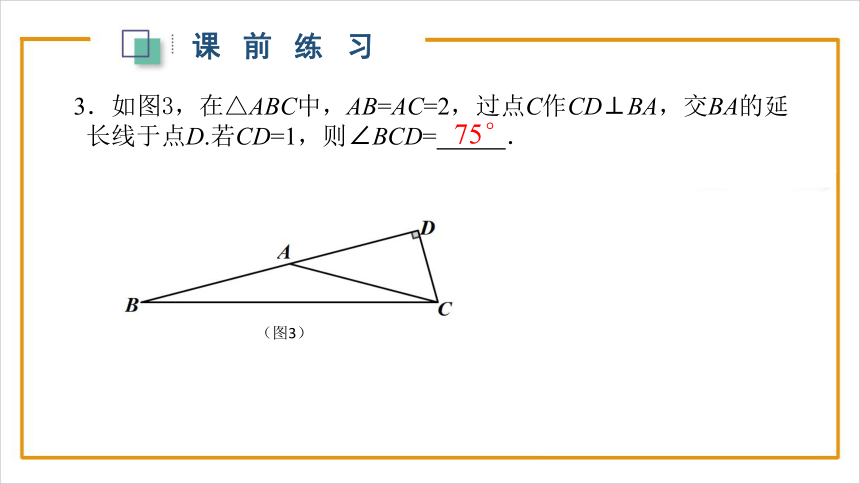
3.如图3,在△ABC中,AB=AC=2,过点C作CD⊥BA,交BA的延长线于点D.若CD=1,则∠BCD= .
(图3)
75°
例题精析
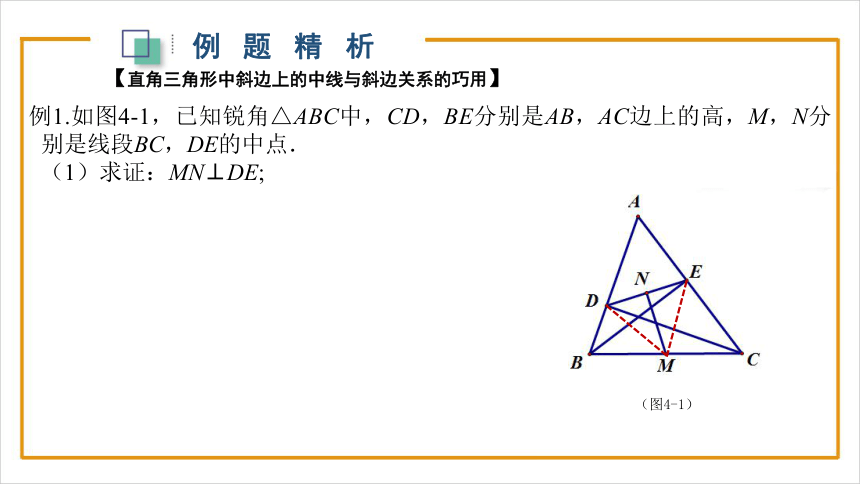
例1.如图4-1,已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE;
【直角三角形中斜边上的中线与斜边关系的巧用】
(图4-1)
例题精析
例1.如图4-1,已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE;
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想;
【直角三角形中斜边上的中线与斜边关系的巧用】
(图4-1)
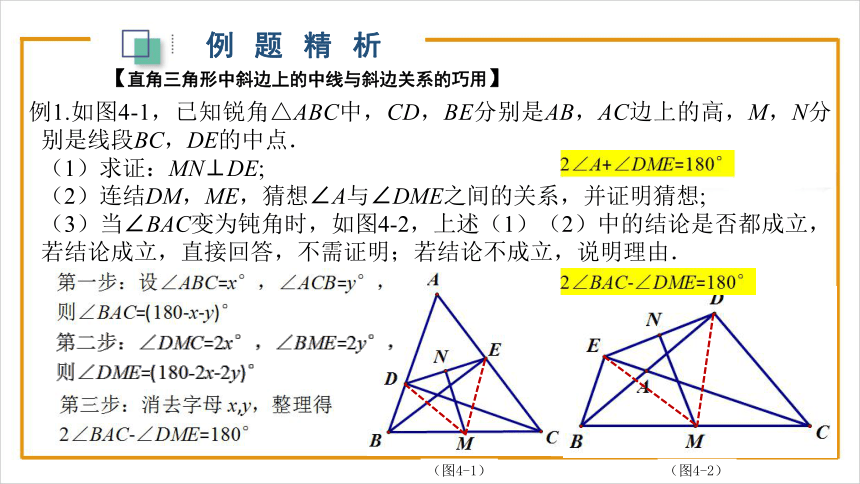
例题精析
例1.如图4-1,已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE;
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想;
(3)当∠BAC变为钝角时,如图4-2,上述(1)(2)中的结论是否都成立,若结论成立,直接回答,不需证明;若结论不成立,说明理由.
【直角三角形中斜边上的中线与斜边关系的巧用】
(图4-1)
(图4-2)
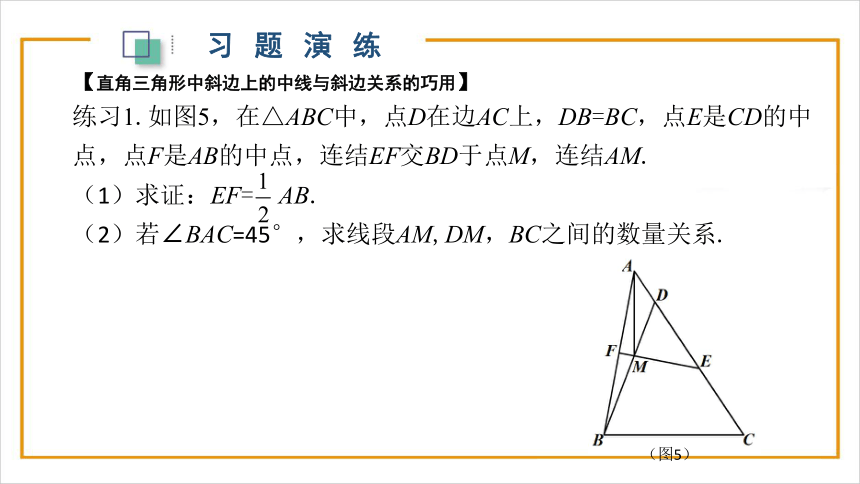
习题演练
【直角三角形中斜边上的中线与斜边关系的巧用】
练习1.如图5,在△ABC中,点D在边AC上,DB=BC,点E是CD的中点,点F是AB的中点,连结EF交BD于点M,连结AM.
(1)求证:EF= AB.
(2)若∠BAC=45°,求线段AM,DM,BC之间的数量关系.
(图5)
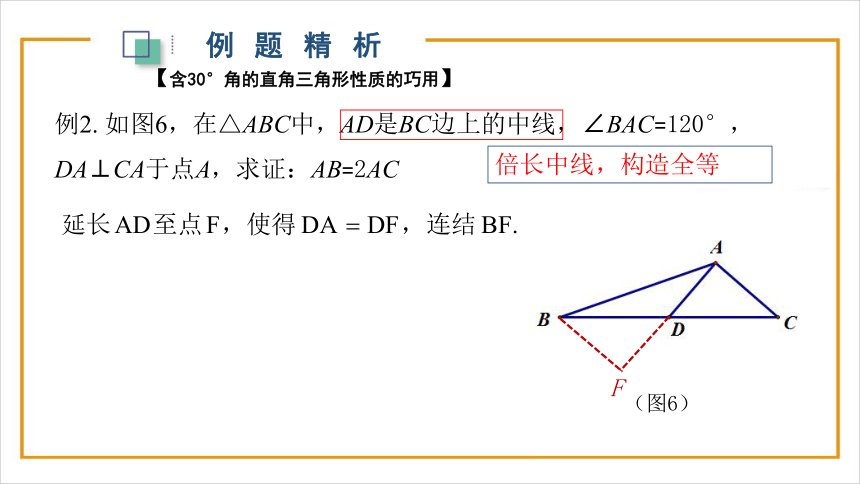
例2. 如图6,在△ABC中,AD是BC边上的中线,∠BAC=120°,DA⊥CA于点A,求证:AB=2AC
例题精析
【含30°角的直角三角形性质的巧用】
(图6)
F
倍长中线,构造全等
习题演练
【含30°角的直角三角形性质的巧用】
练习2.如图7,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=12,DE=4,求BC的长.
(图7)
等边三角形
例3.喜欢数学的小婷同学在家用几何画板研究几何图形:
(1)她首先绘制了一个以线段AB为斜边的等腰直角三角形ABC,如图8-1,然后以AB中点E为顶点作直角∠DEF分别交AC,BC于点D和点F,她通过度量发现DE和EF的长度是一样的,你知道为什么吗?请你证明.
例题精析
【等腰直角三角形知识的巧用】
(图8-1)
角:内角为90°、45°、45°
边:三边比例:1:1:
线:三线合一且斜边上的中线是斜边的一半
例3.喜欢数学的小婷同学在家用几何画板研究几何图形:
(1)她首先绘制了一个以线段AB为斜边的等腰直角三角形ABC,如图8-1,然后以AB中点E为顶点作直角∠DEF分别交AC,BC于点D和点F,她通过度量发现DE和EF的长度是一样的,你知道为什么吗?请你证明.
例题精析
【等腰直角三角形知识的巧用】
(图8-1)
角:内角为90°、45°、45°
边:三边比例:1:1:
线:三线合一且斜边上的中线是斜边的一半
例3.(2)接下来,小婷同学又绘制了一个一般的直角△ABC,如图8-2,以斜边AB中点E为顶点作直角DEF,分别交AC、BC于点D 、F ,且点A与点G关于直线DE成轴对称,连接DG,FG,小婷同学通过度量发现∠DGF始终是直角,请你证明这个结论.
例题精析
【等腰直角三角形知识的巧用】
(图8-2)
图形全等:边、角相等.
例3.(3)小婷同学发现,如果将题(2)中的一般直角△ABC改成等腰直角△ABC,其他条件不变,如图8-3,无论如何拖动点D,四边形DEFG的面积始终等于4,请问当CD=1时,四边形EDGF的周长为 .
例题精析
【等腰直角三角形知识的巧用】
(图8-3)
例3.(3)小婷同学发现,如果将题(2)中的一般直角△ABC改成等腰直角△ABC,其他条件不变,如图8-3,无论如何拖动点D,四边形DEFG的面积始终等于4,请问当CD=1时,四边形EDGF的周长为 .
例题精析
【等腰直角三角形知识的巧用】
(图8-3)
H
习题演练
【等腰直角三角形知识的巧用】
练习3.如图9,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在的直线于点F.
(1)当点E在线段BD上移动时,如图9-1,求证:BC-DE= DF.
(图9-1)
习题演练
【等腰直角三角形知识的巧用】
练习3.如图9,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在的直线于点F.
(1)当点E在线段BD上移动时,如图9-1,求证:BC-DE= DF.
(2)当点E在直线BD上移动时,如图9-2、图9-3,线段BC,DE与DF又有怎样的数量关系?请直接写出你的猜想.
(图9-1)
(图9-3)
(图9-2)
习题演练
【等腰直角三角形知识的巧用】
练习3.如图9,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在的直线于点F.
(1)当点E在线段BD上移动时,如图9-1,求证:BC-DE= DF.
(2)当点E在直线BD上移动时,如图9-2、图9-3,线段BC,DE与DF又有怎样的数量关系?请直接写出你的猜想.
(图9-1)
(图9-3)
(图9-2)
课后练习
1.如图10,在△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连结BD,DE,BE.有下列结论:①∠ECA=165°;②BE=BC;③AD=BE;④CD=BD.其中正确的结论是 .
(图10)
2.如图11,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求BQ的长.
课后练习
(图11)
3.如图,已知△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,D为AB边的中点,将等腰直角△DMN的45°角的顶点放置于D点,其斜边及一条直角边分别与△ABC的AC、BC边相交于点E、F(点E不与点C、A重合;点F不与点C、B重合),连结EF,以D点为旋转中心旋转等腰直角△DMN,问△CEF的周长是否发生变化?说明理由.
P
课后练习
习题演练
【等腰直角三角形知识的巧用】
P
专题三 直角三角形
八 年 级 数 学
内容提要
利用直角三角形基本结论、基本图形解决问题
直角三角形斜边上的 中线与斜边的关系
特殊直角三角形
含30°的直角三角形
含45°的直角三角形
三边之比为
三边之比为
直角三角形的性质巧用
添辅助线、构造全等等
课前练习
58°
12
课前练习
3.如图3,在△ABC中,AB=AC=2,过点C作CD⊥BA,交BA的延长线于点D.若CD=1,则∠BCD= .
(图3)
75°
例题精析
例1.如图4-1,已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE;
【直角三角形中斜边上的中线与斜边关系的巧用】
(图4-1)
例题精析
例1.如图4-1,已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE;
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想;
【直角三角形中斜边上的中线与斜边关系的巧用】
(图4-1)
例题精析
例1.如图4-1,已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE;
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想;
(3)当∠BAC变为钝角时,如图4-2,上述(1)(2)中的结论是否都成立,若结论成立,直接回答,不需证明;若结论不成立,说明理由.
【直角三角形中斜边上的中线与斜边关系的巧用】
(图4-1)
(图4-2)
习题演练
【直角三角形中斜边上的中线与斜边关系的巧用】
练习1.如图5,在△ABC中,点D在边AC上,DB=BC,点E是CD的中点,点F是AB的中点,连结EF交BD于点M,连结AM.
(1)求证:EF= AB.
(2)若∠BAC=45°,求线段AM,DM,BC之间的数量关系.
(图5)
例2. 如图6,在△ABC中,AD是BC边上的中线,∠BAC=120°,DA⊥CA于点A,求证:AB=2AC
例题精析
【含30°角的直角三角形性质的巧用】
(图6)
F
倍长中线,构造全等
习题演练
【含30°角的直角三角形性质的巧用】
练习2.如图7,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=12,DE=4,求BC的长.
(图7)
等边三角形
例3.喜欢数学的小婷同学在家用几何画板研究几何图形:
(1)她首先绘制了一个以线段AB为斜边的等腰直角三角形ABC,如图8-1,然后以AB中点E为顶点作直角∠DEF分别交AC,BC于点D和点F,她通过度量发现DE和EF的长度是一样的,你知道为什么吗?请你证明.
例题精析
【等腰直角三角形知识的巧用】
(图8-1)
角:内角为90°、45°、45°
边:三边比例:1:1:
线:三线合一且斜边上的中线是斜边的一半
例3.喜欢数学的小婷同学在家用几何画板研究几何图形:
(1)她首先绘制了一个以线段AB为斜边的等腰直角三角形ABC,如图8-1,然后以AB中点E为顶点作直角∠DEF分别交AC,BC于点D和点F,她通过度量发现DE和EF的长度是一样的,你知道为什么吗?请你证明.
例题精析
【等腰直角三角形知识的巧用】
(图8-1)
角:内角为90°、45°、45°
边:三边比例:1:1:
线:三线合一且斜边上的中线是斜边的一半
例3.(2)接下来,小婷同学又绘制了一个一般的直角△ABC,如图8-2,以斜边AB中点E为顶点作直角DEF,分别交AC、BC于点D 、F ,且点A与点G关于直线DE成轴对称,连接DG,FG,小婷同学通过度量发现∠DGF始终是直角,请你证明这个结论.
例题精析
【等腰直角三角形知识的巧用】
(图8-2)
图形全等:边、角相等.
例3.(3)小婷同学发现,如果将题(2)中的一般直角△ABC改成等腰直角△ABC,其他条件不变,如图8-3,无论如何拖动点D,四边形DEFG的面积始终等于4,请问当CD=1时,四边形EDGF的周长为 .
例题精析
【等腰直角三角形知识的巧用】
(图8-3)
例3.(3)小婷同学发现,如果将题(2)中的一般直角△ABC改成等腰直角△ABC,其他条件不变,如图8-3,无论如何拖动点D,四边形DEFG的面积始终等于4,请问当CD=1时,四边形EDGF的周长为 .
例题精析
【等腰直角三角形知识的巧用】
(图8-3)
H
习题演练
【等腰直角三角形知识的巧用】
练习3.如图9,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在的直线于点F.
(1)当点E在线段BD上移动时,如图9-1,求证:BC-DE= DF.
(图9-1)
习题演练
【等腰直角三角形知识的巧用】
练习3.如图9,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在的直线于点F.
(1)当点E在线段BD上移动时,如图9-1,求证:BC-DE= DF.
(2)当点E在直线BD上移动时,如图9-2、图9-3,线段BC,DE与DF又有怎样的数量关系?请直接写出你的猜想.
(图9-1)
(图9-3)
(图9-2)
习题演练
【等腰直角三角形知识的巧用】
练习3.如图9,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在的直线于点F.
(1)当点E在线段BD上移动时,如图9-1,求证:BC-DE= DF.
(2)当点E在直线BD上移动时,如图9-2、图9-3,线段BC,DE与DF又有怎样的数量关系?请直接写出你的猜想.
(图9-1)
(图9-3)
(图9-2)
课后练习
1.如图10,在△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连结BD,DE,BE.有下列结论:①∠ECA=165°;②BE=BC;③AD=BE;④CD=BD.其中正确的结论是 .
(图10)
2.如图11,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求BQ的长.
课后练习
(图11)
3.如图,已知△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,D为AB边的中点,将等腰直角△DMN的45°角的顶点放置于D点,其斜边及一条直角边分别与△ABC的AC、BC边相交于点E、F(点E不与点C、A重合;点F不与点C、B重合),连结EF,以D点为旋转中心旋转等腰直角△DMN,问△CEF的周长是否发生变化?说明理由.
P
课后练习
习题演练
【等腰直角三角形知识的巧用】
P
