人教版数学九年级上册 24.1.4 圆周角 课件(共23张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.1.4 圆周角 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 753.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 19:25:39 | ||
图片预览


文档简介
(共23张PPT)
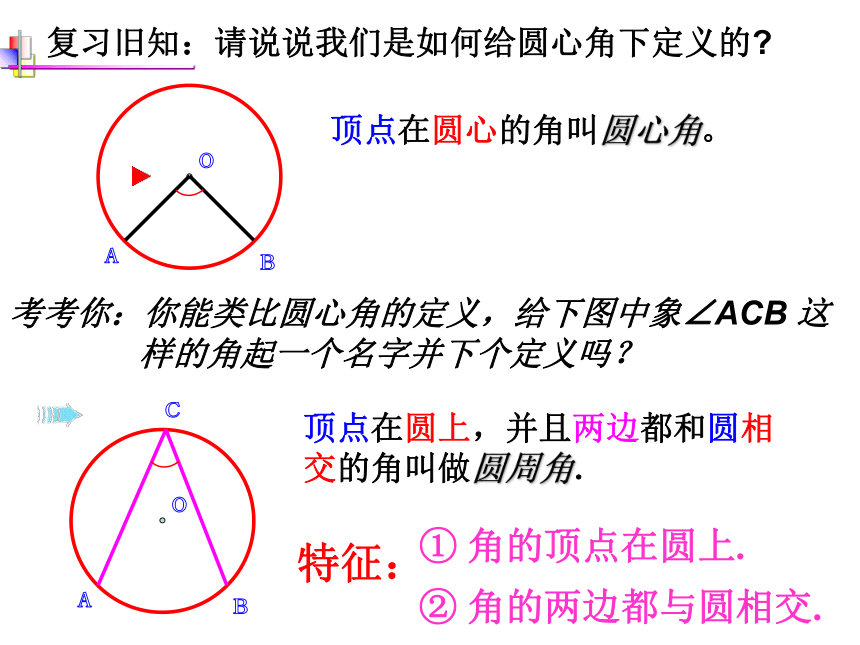
复习旧知:请说说我们是如何给圆心角下定义的
顶点在圆心的角叫圆心角。
考考你:你能类比圆心角的定义,给下图中象∠ACB 这
样的角起一个名字并下个定义吗?
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
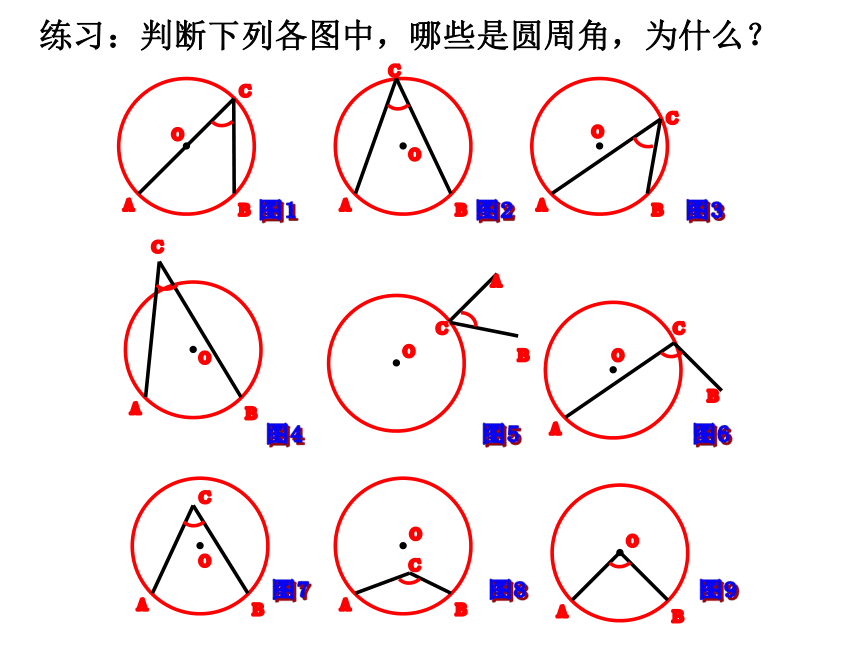
练习:判断下列各图中,哪些是圆周角,为什么?
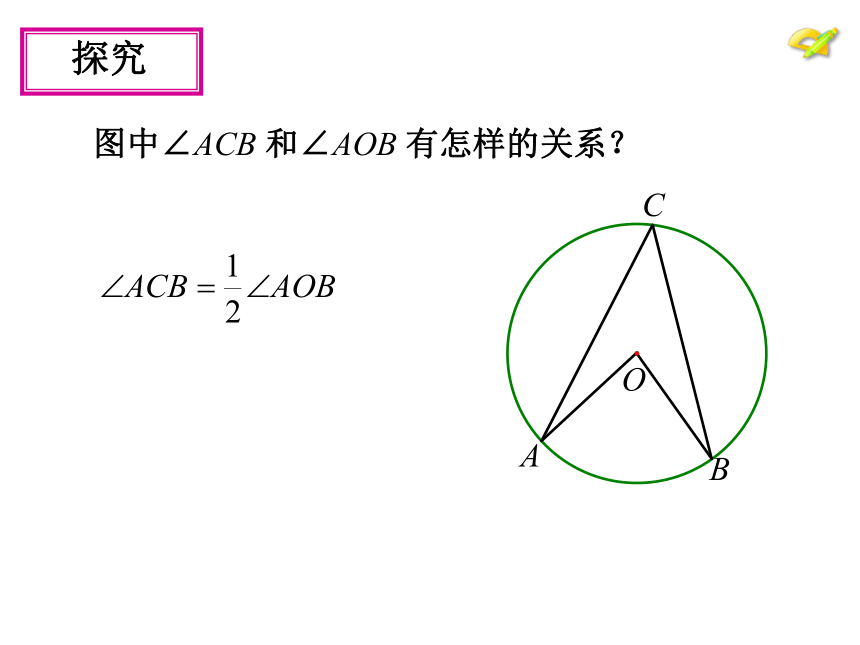
图中∠ACB 和∠AOB 有怎样的关系?
探究
B
C
O
A
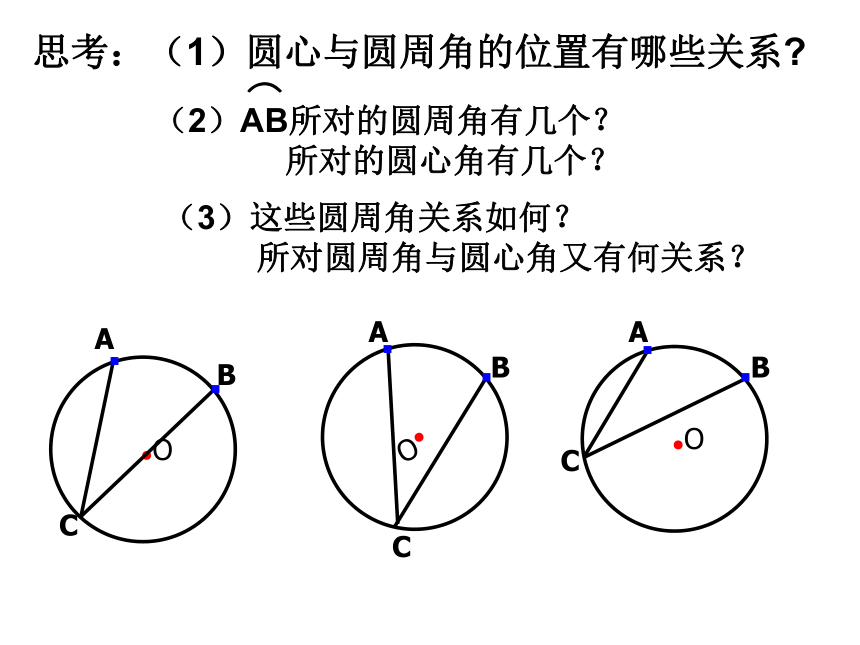
思考:(1)圆心与圆周角的位置有哪些关系
●O
A
C
B
●O
A
C
B
●O
A
C
B
·
·
·
·
·
·
⌒
(2)AB所对的圆周角有几个?
所对的圆心角有几个?
(3)这些圆周角关系如何?
所对圆周角与圆心角又有何关系?
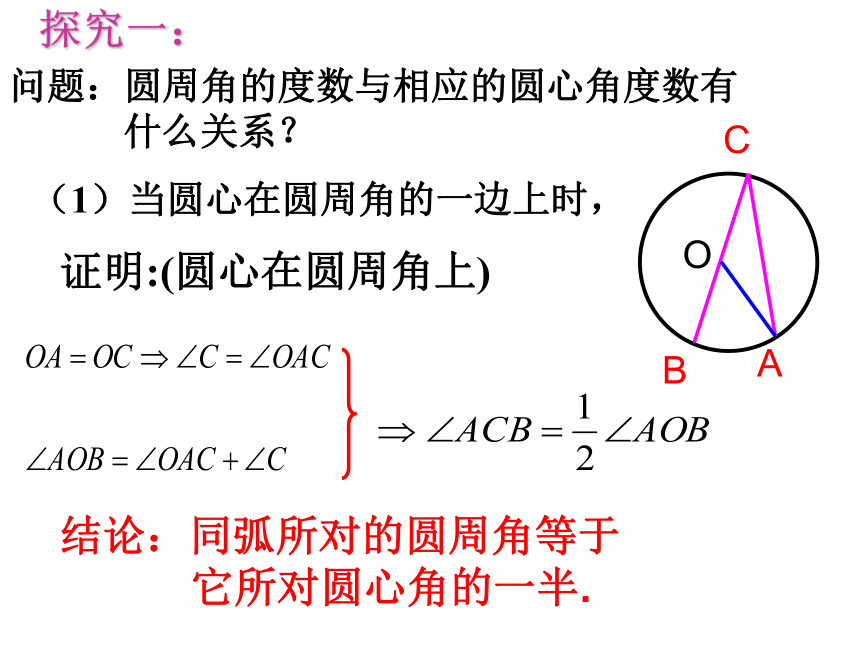
问题:圆周角的度数与相应的圆心角度数有
什么关系?
(1)当圆心在圆周角的一边上时,
探究一:
证明:(圆心在圆周角上)
结论:同弧所对的圆周角等于
它所对圆心角的一半.
A
O
B
C
(2).当圆心在圆周角内部时,
提示:能否转化为1的情况
过点C作直径CD.由1可得:
∴ ∠ACB = ∠AOB.
∠ACD = ∠AOD,∠BCD = ∠BOD,
●O
A
C
B
D
结论: 同弧所对的圆周角等于
它所对圆心角的一半.
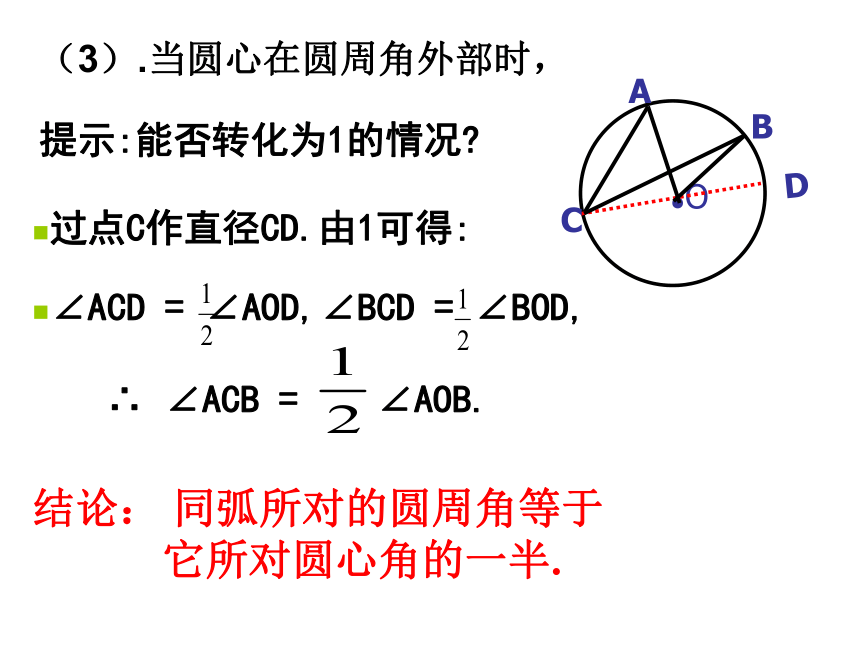
(3).当圆心在圆周角外部时,
提示:能否转化为1的情况
过点C作直径CD.由1可得:
∴ ∠ACB = ∠AOB.
∠ACD = ∠AOD,∠BCD = ∠BOD,
●O
D
A
C
B
结论: 同弧所对的圆周角等于
它所对圆心角的一半.
·
A
B
C
D
E
O
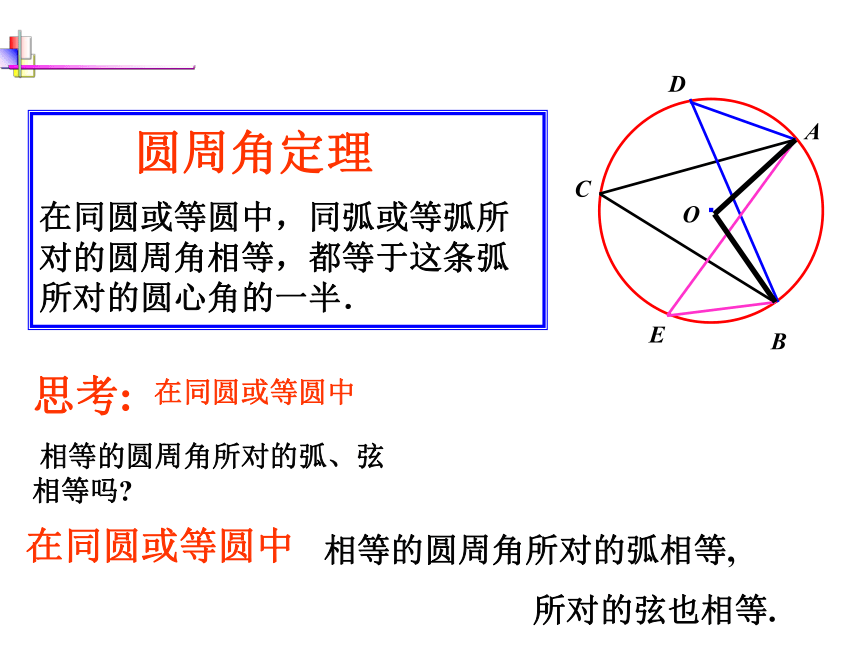
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
思考:
相等的圆周角所对的弧、弦相等吗
在同圆或等圆中
在同圆或等圆中
相等的圆周角所对的弧相等,
所对的弦也相等.
2.如图,圆心角∠AOB=100°,
则∠ACB= ;
O
A
B
C
1.求圆中角X的度数
B
A
O
.
70°
x
A
O
.
X
120°
130°
x=35°
x=120°
练习:
3.试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠1=∠4
∠2=∠7
∠3=∠6
∠5=∠8
练习:
方法点拔:由同弧来找相等的圆周角
4.已知⊙O中弦AB等于半径,则弦AB所对的圆心角的度数是____,圆周角的度数是___________.
O
A
B
60°
30°
或150°
练习:
A
C
B
E
D
同圆或等圆中,同弦或等弦所对的圆周角相等或互补。
练习5. 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。
问船在航行时怎样才能保证不进入暗礁区
(1)当船与两个灯塔的夹角∠α大于“危险角”时,船是否进入暗礁区?为什么?
(2)当船与两个灯塔的夹角∠α小于“危险角”时,船是否进入暗礁区?为什么?
小结: 圆外角<圆周角 <圆内角
A
B
O
C
如图,AB是直径,则∠ACB=____
90 度
直径(或半圆)所对的圆周角是直角。
90度的圆周角所对的弦是直径。
圆周角定理的推论:
想一想
三、应用举例
解
例1 如图,AB是⊙O的直径,∠A=80°.
求∠ABC的度数.
因为AB是⊙O的直径,而直径所对的圆周角是直角,所以
∠ABC=180°-∠A-∠ACB
=180°-80°-90°
=10°
例2.如图AB是⊙O的直径,M是劣弧AC的中点,弦BM与 AC相交于点D,若∠ABC=2∠A。
求证:AD=2DC。
证明:∵ AB是⊙O的直径
∴∠C是直角
∴∠A+∠ABC=90°
又∵ ∠ABC=2∠A
∴ ∠ABC=60° ∠A=30°
而M是劣弧AC的中点
∴ ∠CBM= ∠ABM=30°
∴ ∠A= ∠ABM
∴AD=DB
在RT△BCD中, ∠CBM =30°
∴BD=2DC
∴ AD=2DC
A
B
C
D
O
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
四边形ABCD是⊙O的内接四边形;
四边形ABCD是⊙O的内接四边形,你能说出它们对角的关系吗
A
B
C
D
O
圆内接四边形的对角互补。
例3: 如图,AB是⊙O的直径AB=10cm,
弦AC=6cm,∠ACB的平分线交⊙O于点D . 求 BC, AD ,BD 的长.
10
6
例4:如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,求∠BCD的度数.
A
B
O
C
D
40°
50°
课堂小结
1. 【圆周角的定义】
2. 【圆周角的性质】
(1)在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;
(3)半圆或直径所对的圆周角是直角;
顶点在圆上,两边都与圆相交的角叫做圆周角。
(2)在同圆(或等圆)中,相等的圆周角所对的弧相等;
(4) 90°的圆周角所对的弦是圆的直径。
复习旧知:请说说我们是如何给圆心角下定义的
顶点在圆心的角叫圆心角。
考考你:你能类比圆心角的定义,给下图中象∠ACB 这
样的角起一个名字并下个定义吗?
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
练习:判断下列各图中,哪些是圆周角,为什么?
图中∠ACB 和∠AOB 有怎样的关系?
探究
B
C
O
A
思考:(1)圆心与圆周角的位置有哪些关系
●O
A
C
B
●O
A
C
B
●O
A
C
B
·
·
·
·
·
·
⌒
(2)AB所对的圆周角有几个?
所对的圆心角有几个?
(3)这些圆周角关系如何?
所对圆周角与圆心角又有何关系?
问题:圆周角的度数与相应的圆心角度数有
什么关系?
(1)当圆心在圆周角的一边上时,
探究一:
证明:(圆心在圆周角上)
结论:同弧所对的圆周角等于
它所对圆心角的一半.
A
O
B
C
(2).当圆心在圆周角内部时,
提示:能否转化为1的情况
过点C作直径CD.由1可得:
∴ ∠ACB = ∠AOB.
∠ACD = ∠AOD,∠BCD = ∠BOD,
●O
A
C
B
D
结论: 同弧所对的圆周角等于
它所对圆心角的一半.
(3).当圆心在圆周角外部时,
提示:能否转化为1的情况
过点C作直径CD.由1可得:
∴ ∠ACB = ∠AOB.
∠ACD = ∠AOD,∠BCD = ∠BOD,
●O
D
A
C
B
结论: 同弧所对的圆周角等于
它所对圆心角的一半.
·
A
B
C
D
E
O
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
思考:
相等的圆周角所对的弧、弦相等吗
在同圆或等圆中
在同圆或等圆中
相等的圆周角所对的弧相等,
所对的弦也相等.
2.如图,圆心角∠AOB=100°,
则∠ACB= ;
O
A
B
C
1.求圆中角X的度数
B
A
O
.
70°
x
A
O
.
X
120°
130°
x=35°
x=120°
练习:
3.试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠1=∠4
∠2=∠7
∠3=∠6
∠5=∠8
练习:
方法点拔:由同弧来找相等的圆周角
4.已知⊙O中弦AB等于半径,则弦AB所对的圆心角的度数是____,圆周角的度数是___________.
O
A
B
60°
30°
或150°
练习:
A
C
B
E
D
同圆或等圆中,同弦或等弦所对的圆周角相等或互补。
练习5. 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。
问船在航行时怎样才能保证不进入暗礁区
(1)当船与两个灯塔的夹角∠α大于“危险角”时,船是否进入暗礁区?为什么?
(2)当船与两个灯塔的夹角∠α小于“危险角”时,船是否进入暗礁区?为什么?
小结: 圆外角<圆周角 <圆内角
A
B
O
C
如图,AB是直径,则∠ACB=____
90 度
直径(或半圆)所对的圆周角是直角。
90度的圆周角所对的弦是直径。
圆周角定理的推论:
想一想
三、应用举例
解
例1 如图,AB是⊙O的直径,∠A=80°.
求∠ABC的度数.
因为AB是⊙O的直径,而直径所对的圆周角是直角,所以
∠ABC=180°-∠A-∠ACB
=180°-80°-90°
=10°
例2.如图AB是⊙O的直径,M是劣弧AC的中点,弦BM与 AC相交于点D,若∠ABC=2∠A。
求证:AD=2DC。
证明:∵ AB是⊙O的直径
∴∠C是直角
∴∠A+∠ABC=90°
又∵ ∠ABC=2∠A
∴ ∠ABC=60° ∠A=30°
而M是劣弧AC的中点
∴ ∠CBM= ∠ABM=30°
∴ ∠A= ∠ABM
∴AD=DB
在RT△BCD中, ∠CBM =30°
∴BD=2DC
∴ AD=2DC
A
B
C
D
O
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
四边形ABCD是⊙O的内接四边形;
四边形ABCD是⊙O的内接四边形,你能说出它们对角的关系吗
A
B
C
D
O
圆内接四边形的对角互补。
例3: 如图,AB是⊙O的直径AB=10cm,
弦AC=6cm,∠ACB的平分线交⊙O于点D . 求 BC, AD ,BD 的长.
10
6
例4:如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,求∠BCD的度数.
A
B
O
C
D
40°
50°
课堂小结
1. 【圆周角的定义】
2. 【圆周角的性质】
(1)在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;
(3)半圆或直径所对的圆周角是直角;
顶点在圆上,两边都与圆相交的角叫做圆周角。
(2)在同圆(或等圆)中,相等的圆周角所对的弧相等;
(4) 90°的圆周角所对的弦是圆的直径。
同课章节目录
