人教版数学九年级上册24.4 弧长和扇形公式 课件(共32张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.4 弧长和扇形公式 课件(共32张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 19:27:58 | ||
图片预览







文档简介
(共32张PPT)
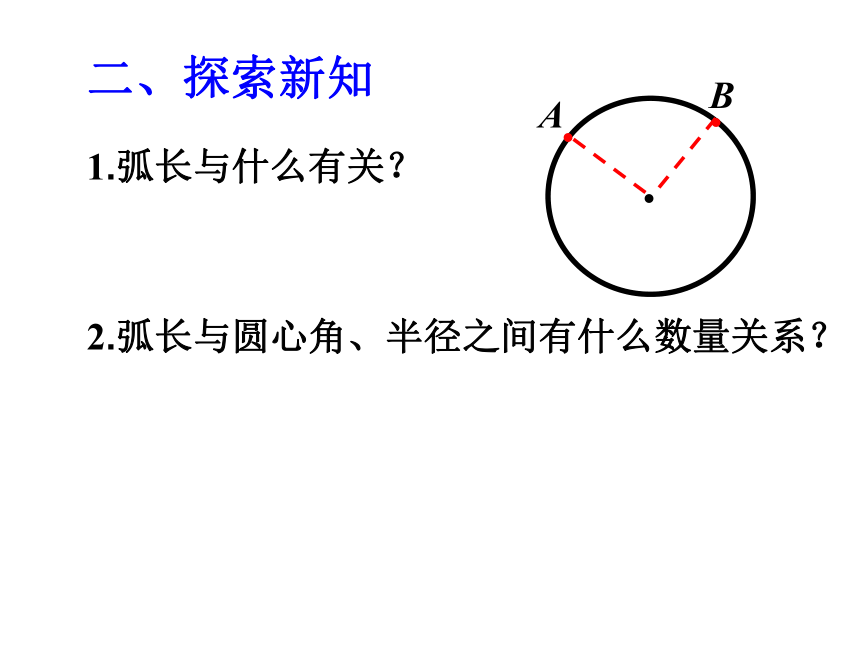
一、温故知新
1.弧的定义是什么?
2.对于弧这个几何元素,我们往往要计算什么量?
弧的度数
弧的长度即弧长
A
B
24.4.1弧长和扇形面积
二、探索新知
1.弧长与什么有关?
A
B
2.弧长与圆心角、半径之间有什么数量关系?
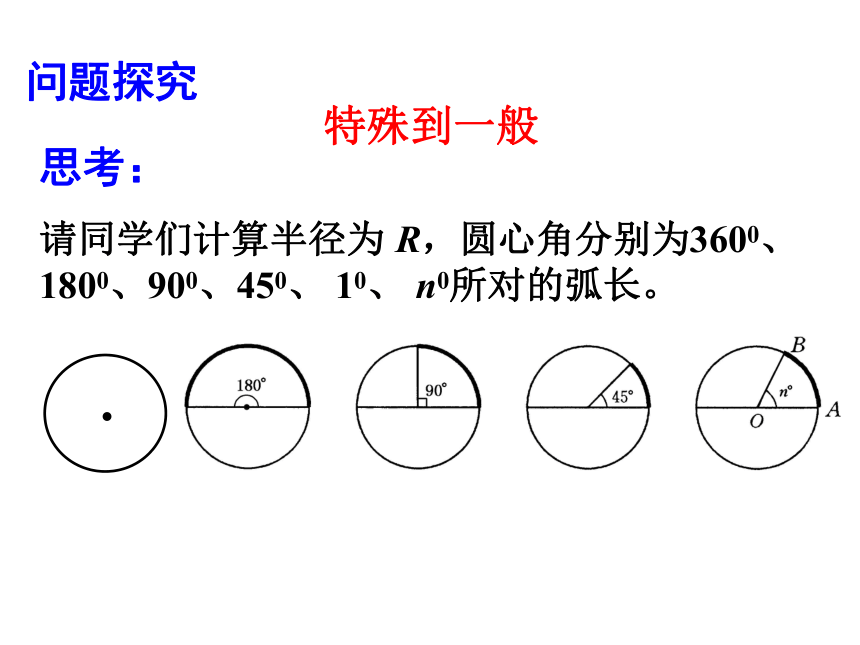
问题探究
思考:
请同学们计算半径为 R,圆心角分别为3600、 1800、900、450、 10、 n0所对的弧长。
特殊到一般
1800
900
450
n0
圆心角占整个周角的
所对弧长是
比 例
结论:
如果弧长为l,圆心角度数为n°,圆的半径
为R,那么,弧长的计算公式为:
注:(1)进行计算时,要注意公式中n的意义,n表示1°圆心角的倍数,它是不带单位的;
(2)区分弧、弧的度数、弧长三概念.
度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
例1.已知圆弧的半径为50厘米,圆心角为60°,求此圆弧的长度。
解:
=
(cm)
答:此圆弧的长度为
cm
三、知识应用
练一练
1.半径为3cm,弧长是 cm,该弧所对的圆心角是多少度?
2.圆心角为3000,所对的弧长为10 m,求该圆的半径.
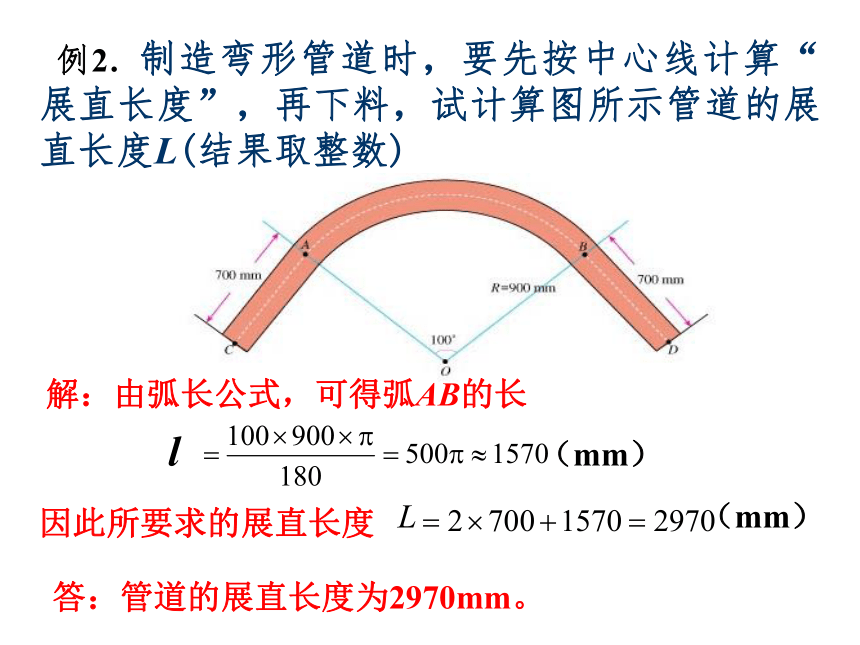
例2. 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(结果取整数)
解:由弧长公式,可得弧AB的长
l (mm)
因此所要求的展直长度
L (mm)
答:管道的展直长度为2970mm。
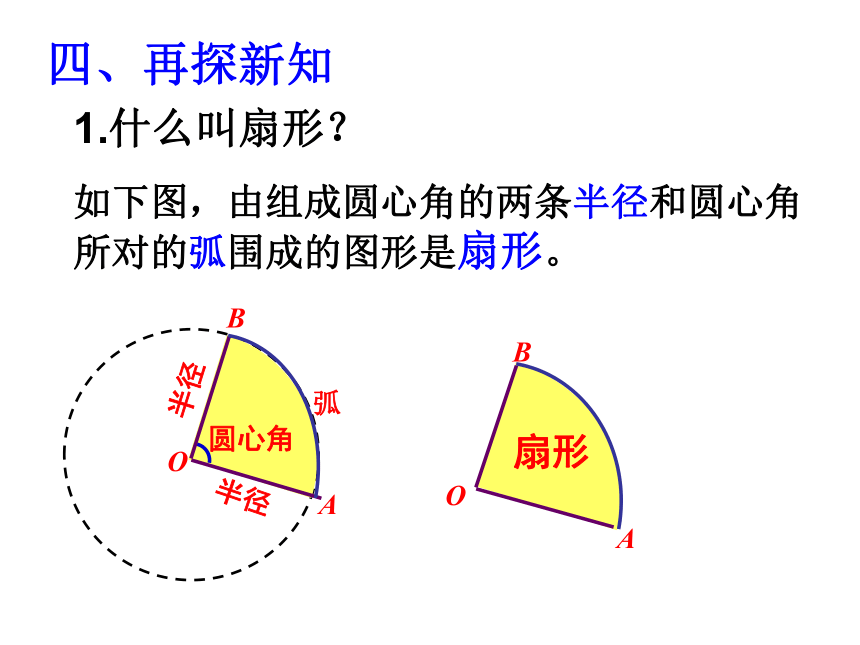
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
四、再探新知
1.什么叫扇形?
2.类比于弧长的推导过程,你能推导扇形的面积公式吗?
扇形面积公式
若设⊙O半径为R,圆心角为n°的扇形的面积S扇形,则
注意:
公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
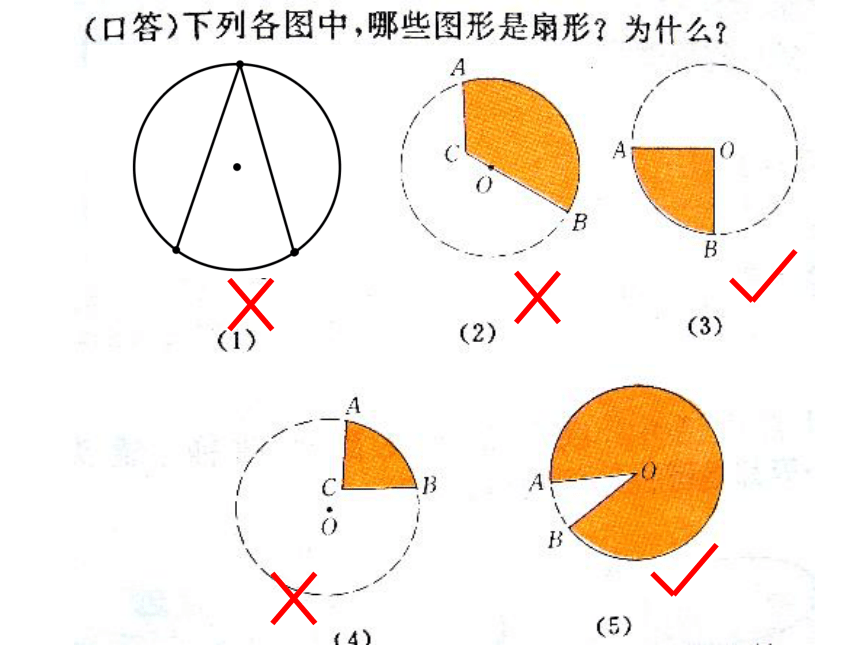
1.已知扇形的圆心角为120°,半径为2,则这个扇形的面积为多少?
五、应用新知
2.已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是______cm2,
问题:扇形的弧长公式与面积公式有联系吗?
2.已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是______cm2,
3.如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。(精确到0.01m)。
0
B
A
C
D
弓形的面积 = S扇- S△
变式:如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.9m,求截面上有水部分的面积。
0
A
B
D
C
E
弓形的面积 = S扇+ S△
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
规律提升
0
0
弓形的面积是扇形的面积与三角形
面积的和或差
4.如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中阴影部分的面积是多少?
B
5.如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图①的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图②位置时,顶点A1所经过的路径长为 .
三要素:旋转中心、旋转方向、旋转角
图①
图②
通过本节课的学到了什么?
体会分享
课外思考题
1. O 中, ,AB=3,
求弧AB的长.
2.如图,矩形ABCD中,AB=4,AB=3,该矩形在直线l上向右作无滑动翻滚,第一次翻滚时点A到达点A1,第二次翻滚时遇有小木块挡住了,点A1到达点A2 , A 2D1E=30 0 ,求两次翻滚点A经过的路径长.
3. O中,弦BC∥OA,AB
切 O于点B,AB=3 ,OA=2 ,求弧BC的长.
5.正三角形ABC中,AB=1,正三角形ABC在一条直线上做无滑动滚动,若滚动一周,求点A经过的路径的长度。
一、温故知新
1.弧的定义是什么?
2.对于弧这个几何元素,我们往往要计算什么量?
弧的度数
弧的长度即弧长
A
B
24.4.1弧长和扇形面积
二、探索新知
1.弧长与什么有关?
A
B
2.弧长与圆心角、半径之间有什么数量关系?
问题探究
思考:
请同学们计算半径为 R,圆心角分别为3600、 1800、900、450、 10、 n0所对的弧长。
特殊到一般
1800
900
450
n0
圆心角占整个周角的
所对弧长是
比 例
结论:
如果弧长为l,圆心角度数为n°,圆的半径
为R,那么,弧长的计算公式为:
注:(1)进行计算时,要注意公式中n的意义,n表示1°圆心角的倍数,它是不带单位的;
(2)区分弧、弧的度数、弧长三概念.
度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
例1.已知圆弧的半径为50厘米,圆心角为60°,求此圆弧的长度。
解:
=
(cm)
答:此圆弧的长度为
cm
三、知识应用
练一练
1.半径为3cm,弧长是 cm,该弧所对的圆心角是多少度?
2.圆心角为3000,所对的弧长为10 m,求该圆的半径.
例2. 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(结果取整数)
解:由弧长公式,可得弧AB的长
l (mm)
因此所要求的展直长度
L (mm)
答:管道的展直长度为2970mm。
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
四、再探新知
1.什么叫扇形?
2.类比于弧长的推导过程,你能推导扇形的面积公式吗?
扇形面积公式
若设⊙O半径为R,圆心角为n°的扇形的面积S扇形,则
注意:
公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
1.已知扇形的圆心角为120°,半径为2,则这个扇形的面积为多少?
五、应用新知
2.已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是______cm2,
问题:扇形的弧长公式与面积公式有联系吗?
2.已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是______cm2,
3.如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。(精确到0.01m)。
0
B
A
C
D
弓形的面积 = S扇- S△
变式:如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.9m,求截面上有水部分的面积。
0
A
B
D
C
E
弓形的面积 = S扇+ S△
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
规律提升
0
0
弓形的面积是扇形的面积与三角形
面积的和或差
4.如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中阴影部分的面积是多少?
B
5.如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图①的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图②位置时,顶点A1所经过的路径长为 .
三要素:旋转中心、旋转方向、旋转角
图①
图②
通过本节课的学到了什么?
体会分享
课外思考题
1. O 中, ,AB=3,
求弧AB的长.
2.如图,矩形ABCD中,AB=4,AB=3,该矩形在直线l上向右作无滑动翻滚,第一次翻滚时点A到达点A1,第二次翻滚时遇有小木块挡住了,点A1到达点A2 , A 2D1E=30 0 ,求两次翻滚点A经过的路径长.
3. O中,弦BC∥OA,AB
切 O于点B,AB=3 ,OA=2 ,求弧BC的长.
5.正三角形ABC中,AB=1,正三角形ABC在一条直线上做无滑动滚动,若滚动一周,求点A经过的路径的长度。
同课章节目录
