人教版九年级下册 27.1 图形的相似 课件(27张PPT)
文档属性
| 名称 | 人教版九年级下册 27.1 图形的相似 课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
27.1 图形的相似(2)
人教版 数学 九年级 下册
全等图形:
指能够完全重合的两个图形,
观察
即它们的形状和大小完全相同。
复习旧知
知识点 1
相似图形的定义
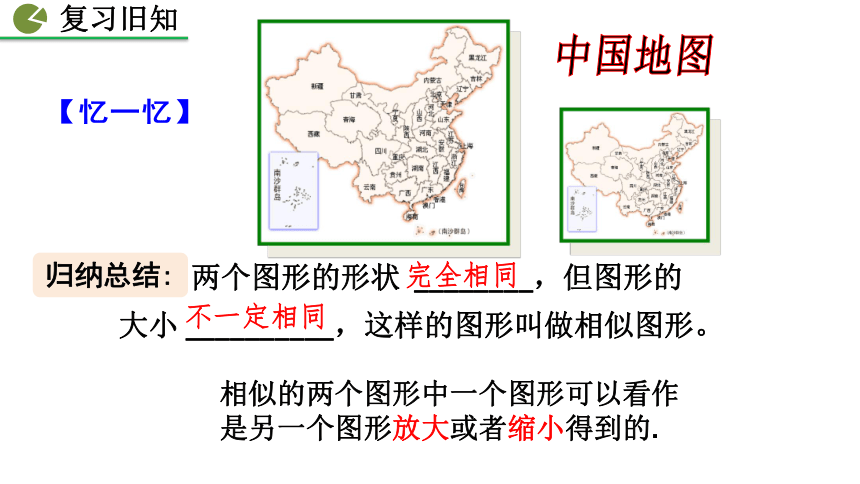
两个图形的形状 ________,但图形的大小 __________,这样的图形叫做相似图形。
完全相同
不一定相同
归纳总结:
中国地图
【忆一忆】
相似的两个图形中一个图形可以看作是另一个图形放大或者缩小得到的.
复习旧知
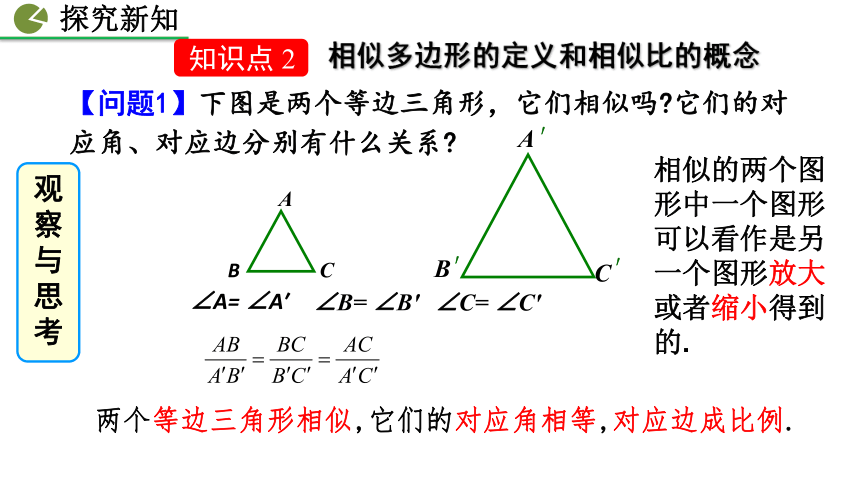
【问题1】下图是两个等边三角形,它们相似吗 它们的对应角、对应边分别有什么关系
B
C
A
B
′
C
A
′
′
∠A= ∠A′
∠B= ∠B′
∠C= ∠C′
两个等边三角形相似,它们的对应角相等,对应边成比例.
探究新知
观
察
与
思
考
知识点 2
相似多边形的定义和相似比的概念
相似的两个图形中一个图形可以看作是另一个图形放大或者缩小得到的.
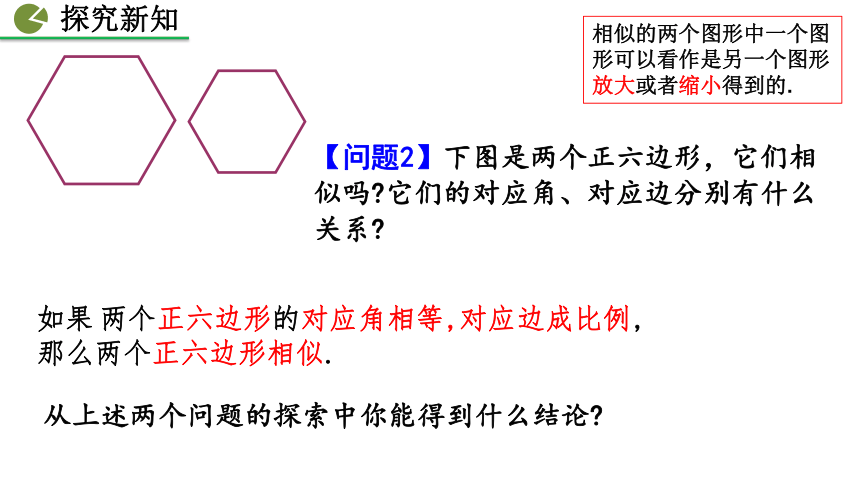
两个正六边形的对应角相等,对应边成比例,
从上述两个问题的探索中你能得到什么结论
探究新知
相似的两个图形中一个图形可以看作是另一个图形放大或者缩小得到的.
如果
那么两个正六边形相似.
【问题2】下图是两个正六边形,它们相似吗 它们的对应角、对应边分别有什么关系
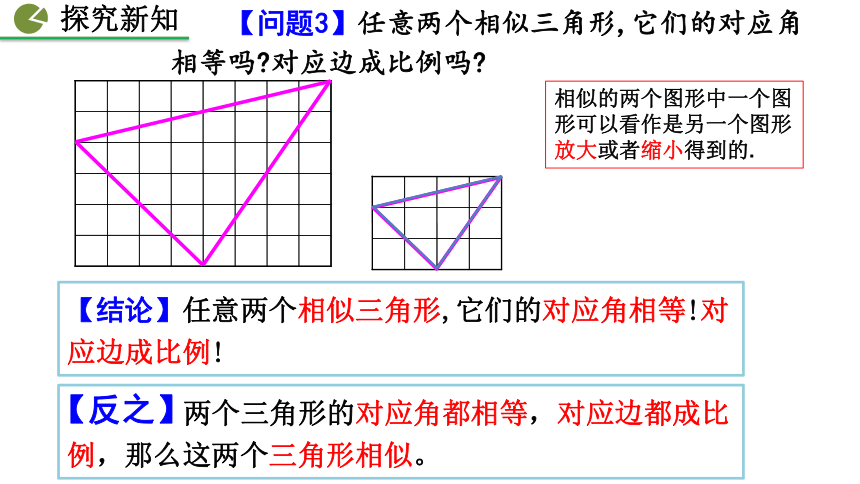
【问题3】任意两个相似三角形,它们的对应角相等吗 对应边成比例吗
【结论】任意两个相似三角形,它们的对应角相等!对应边成比例!
探究新知
相似的两个图形中一个图形可以看作是另一个图形放大或者缩小得到的.
两个三角形的对应角都相等,对应边都成比例,那么这两个三角形相似。
【反之】
1.相似多边形的性质:
相似多边形对应边成比例,对应角相等.
符号语言(以四边形为例)---性质应用:
∵四边形ABCD ∽四边形A′B′C′D′
(相似多边形的对应边成比例,对应角相等)
归纳总结
“∽”表示相似,读作相似于。
符号语言(以四边形为例)---定义法:
∴四边形ABCD ∽四边形A′B′C′D′
(对应角相等,对应边成比例的两个多边形相似)
2.相似多边形定义:如果两个多边形的对应角相等,对应边成比例,那么这两个多边形就叫做相似多边形。
归纳总结
“∽”表示相似,读作相似于。
在四边形ABCD 和四边形A′B′C′D′中,
两个多边形的对应角相等,对应边成比例,那么这两个多边形叫做相似多边形.
相似多边形的对应边的比叫作相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的性质:
相似多边形的定义:
对比归纳:
注意:相似比为1时,相似的两个图形全等,因此全等图形是一种特殊的相似图形.
(相似比有顺序)
2.若△ABC与△ A′B′C′ 相似,且AB:A′B′=1:2
则△ABC与△ A′B′C′的相似比是 ,
△ A′B′C′与△ABC的相似比是 .
2
练一练
1.下列给定的6种情况的图形中能够确定图形相似的概率是 .
A.两个半径不相等的圆 B.所有的等边三角形
C.所有的等腰三角形 D.所有的正方形
E.所有的等腰梯形 F.所有的正六边形
例1.如图,△ABC与△DEF相似,∠A= ∠D= 40°,∠C=30°,求∠E和∠F的度数.
解:∵△ABC ∽ △DEF,
∴∠F=∠C=30°
又∵∠D=∠A=40°
∴∠E=180°-∠D-∠F=110°
D
E
F
A
B
C
应用新知
例2 如图,四边形 ABCD 和 EFGH 相似,求角α, 的大小和EH的长度 x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
应用新知
β
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,
∴ 它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
应用新知
∵ 四边形ABCD和EFGH相似,
∴它们的对应边成比例,由此可得
解得 x = 28 .
,即 .
应用新知
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
利用相似多边形的定义求线段、角的值。
教材练习
1.在比例尺为1:10000000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离。
巩固练习
2.如图所示的两个三角形相似吗?为什么?
3. 如图所示的两个五边形相似,求未知边a、b、c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
教材练习
1.在比例尺为1:10000000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离。
解:设两地的实际距离为Xkm,
∵比例尺=图上距离:实际距离
∴1:10000000=0.0003:x
∴x=3000
答:两地的实际距离为3000km。
巩固练习
2、如图所示的两个三角形相似吗?为什么?
解:如图所示,∠A= ∠A′=900
AB=AC=5, A′B′= A′C′=10,
∴∠B= ∠C=450, ∠B′= ∠C′=450,
再由勾股定理得到,
∴∠A= ∠A′,∠B= ∠B′,∠C= ∠C′
∴两个三角形相似。
A
B
C
A′
B′
C′
巩固练习
3. 如图所示的两个五边形相似,求未知边a、b、c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
巩固练习
解:相似多边形的对应边的比相等,由此可得
, , , ,
解得:a=3,b=4.5,c=4,d=6.
所以未知边a,b,c,d的长度分别为3,4.5,4,6.
4.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
巩固练习
C
5.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边为( )
A.3cm B.4cm C.4.5cm D.5cm
C
巩固练习
6. 如图所示的两个矩形相似吗?为什么?如果相似,相似比是多少?
G
F
E
H
1.5
1
A
D
C
B
3
2
解:矩形ABCD相似于矩形EFGH
因为它们的对应角相等,对应边成比例.
相似比为: .
巩固练习
7、如图,把矩形 ABCD 对折,折痕为 EF,若矩形ABCD 与矩形 EABF 相似,AB = 1.
A
B
C
D
E
F
解:∵ E 是 AD 的中点,
∴ .
又∵矩形 ABCD 与矩形 EABF相似,AB=1,
∴ ,
∴ AB2 = AE·BC,
∴ .
解得
拓广探索题
课堂检测
(1)求BC长;
(2)求矩形 ABFE 与矩形 ABCD 的相似比.
A
B
C
D
E
F
解:矩形 ABEF 与矩形ABCD
的相似比为:
拓广探索题
课堂检测
相似图形
形状相同的图形叫做相似图形
相似图形的大小不一定相同
相似多边形对应边的比叫做相似比
对应角相等,对应边成比例
图形的相似
相似多边形
课堂小结
课后作业
作业
内容
教材配套作业
自主安排
1、线段的比:两条线段的比,就是两条线段长度的比.
2、成比例线段:对于四条线段a,b,c,d,如果其中两条线段的比与另两条线段的比相等,如 = (即ad=bc),我们就说这四条线段a,b,c,d是成比例线段,简称比例线段.
注意:(1)四条线段a,b,c,d成比例,
记作a:b=c:d或 = ;
(2)若四条线段满足 ,
则有ad=bc.
说明:
注意
(1)度量单位要相同;
(2)比例线段具有顺序性;
(3)比值不带单位。
动手做一做:
(1)以下各组是四条线段的长,成比例线段的是( )
A. 4,8,3,5
B. 4,8,3,6
D. 8,4,1,3
C. 3,4,5,6
(2)已知线段a=2cm,b=3cm,c=6cm,且a、b、c、d成比例,则d= cm;若a、b、d、c成比例,则d= cm。
4
9
B
27.1 图形的相似(2)
人教版 数学 九年级 下册
全等图形:
指能够完全重合的两个图形,
观察
即它们的形状和大小完全相同。
复习旧知
知识点 1
相似图形的定义
两个图形的形状 ________,但图形的大小 __________,这样的图形叫做相似图形。
完全相同
不一定相同
归纳总结:
中国地图
【忆一忆】
相似的两个图形中一个图形可以看作是另一个图形放大或者缩小得到的.
复习旧知
【问题1】下图是两个等边三角形,它们相似吗 它们的对应角、对应边分别有什么关系
B
C
A
B
′
C
A
′
′
∠A= ∠A′
∠B= ∠B′
∠C= ∠C′
两个等边三角形相似,它们的对应角相等,对应边成比例.
探究新知
观
察
与
思
考
知识点 2
相似多边形的定义和相似比的概念
相似的两个图形中一个图形可以看作是另一个图形放大或者缩小得到的.
两个正六边形的对应角相等,对应边成比例,
从上述两个问题的探索中你能得到什么结论
探究新知
相似的两个图形中一个图形可以看作是另一个图形放大或者缩小得到的.
如果
那么两个正六边形相似.
【问题2】下图是两个正六边形,它们相似吗 它们的对应角、对应边分别有什么关系
【问题3】任意两个相似三角形,它们的对应角相等吗 对应边成比例吗
【结论】任意两个相似三角形,它们的对应角相等!对应边成比例!
探究新知
相似的两个图形中一个图形可以看作是另一个图形放大或者缩小得到的.
两个三角形的对应角都相等,对应边都成比例,那么这两个三角形相似。
【反之】
1.相似多边形的性质:
相似多边形对应边成比例,对应角相等.
符号语言(以四边形为例)---性质应用:
∵四边形ABCD ∽四边形A′B′C′D′
(相似多边形的对应边成比例,对应角相等)
归纳总结
“∽”表示相似,读作相似于。
符号语言(以四边形为例)---定义法:
∴四边形ABCD ∽四边形A′B′C′D′
(对应角相等,对应边成比例的两个多边形相似)
2.相似多边形定义:如果两个多边形的对应角相等,对应边成比例,那么这两个多边形就叫做相似多边形。
归纳总结
“∽”表示相似,读作相似于。
在四边形ABCD 和四边形A′B′C′D′中,
两个多边形的对应角相等,对应边成比例,那么这两个多边形叫做相似多边形.
相似多边形的对应边的比叫作相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的性质:
相似多边形的定义:
对比归纳:
注意:相似比为1时,相似的两个图形全等,因此全等图形是一种特殊的相似图形.
(相似比有顺序)
2.若△ABC与△ A′B′C′ 相似,且AB:A′B′=1:2
则△ABC与△ A′B′C′的相似比是 ,
△ A′B′C′与△ABC的相似比是 .
2
练一练
1.下列给定的6种情况的图形中能够确定图形相似的概率是 .
A.两个半径不相等的圆 B.所有的等边三角形
C.所有的等腰三角形 D.所有的正方形
E.所有的等腰梯形 F.所有的正六边形
例1.如图,△ABC与△DEF相似,∠A= ∠D= 40°,∠C=30°,求∠E和∠F的度数.
解:∵△ABC ∽ △DEF,
∴∠F=∠C=30°
又∵∠D=∠A=40°
∴∠E=180°-∠D-∠F=110°
D
E
F
A
B
C
应用新知
例2 如图,四边形 ABCD 和 EFGH 相似,求角α, 的大小和EH的长度 x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
应用新知
β
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,
∴ 它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
应用新知
∵ 四边形ABCD和EFGH相似,
∴它们的对应边成比例,由此可得
解得 x = 28 .
,即 .
应用新知
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
利用相似多边形的定义求线段、角的值。
教材练习
1.在比例尺为1:10000000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离。
巩固练习
2.如图所示的两个三角形相似吗?为什么?
3. 如图所示的两个五边形相似,求未知边a、b、c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
教材练习
1.在比例尺为1:10000000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离。
解:设两地的实际距离为Xkm,
∵比例尺=图上距离:实际距离
∴1:10000000=0.0003:x
∴x=3000
答:两地的实际距离为3000km。
巩固练习
2、如图所示的两个三角形相似吗?为什么?
解:如图所示,∠A= ∠A′=900
AB=AC=5, A′B′= A′C′=10,
∴∠B= ∠C=450, ∠B′= ∠C′=450,
再由勾股定理得到,
∴∠A= ∠A′,∠B= ∠B′,∠C= ∠C′
∴两个三角形相似。
A
B
C
A′
B′
C′
巩固练习
3. 如图所示的两个五边形相似,求未知边a、b、c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
巩固练习
解:相似多边形的对应边的比相等,由此可得
, , , ,
解得:a=3,b=4.5,c=4,d=6.
所以未知边a,b,c,d的长度分别为3,4.5,4,6.
4.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
巩固练习
C
5.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边为( )
A.3cm B.4cm C.4.5cm D.5cm
C
巩固练习
6. 如图所示的两个矩形相似吗?为什么?如果相似,相似比是多少?
G
F
E
H
1.5
1
A
D
C
B
3
2
解:矩形ABCD相似于矩形EFGH
因为它们的对应角相等,对应边成比例.
相似比为: .
巩固练习
7、如图,把矩形 ABCD 对折,折痕为 EF,若矩形ABCD 与矩形 EABF 相似,AB = 1.
A
B
C
D
E
F
解:∵ E 是 AD 的中点,
∴ .
又∵矩形 ABCD 与矩形 EABF相似,AB=1,
∴ ,
∴ AB2 = AE·BC,
∴ .
解得
拓广探索题
课堂检测
(1)求BC长;
(2)求矩形 ABFE 与矩形 ABCD 的相似比.
A
B
C
D
E
F
解:矩形 ABEF 与矩形ABCD
的相似比为:
拓广探索题
课堂检测
相似图形
形状相同的图形叫做相似图形
相似图形的大小不一定相同
相似多边形对应边的比叫做相似比
对应角相等,对应边成比例
图形的相似
相似多边形
课堂小结
课后作业
作业
内容
教材配套作业
自主安排
1、线段的比:两条线段的比,就是两条线段长度的比.
2、成比例线段:对于四条线段a,b,c,d,如果其中两条线段的比与另两条线段的比相等,如 = (即ad=bc),我们就说这四条线段a,b,c,d是成比例线段,简称比例线段.
注意:(1)四条线段a,b,c,d成比例,
记作a:b=c:d或 = ;
(2)若四条线段满足 ,
则有ad=bc.
说明:
注意
(1)度量单位要相同;
(2)比例线段具有顺序性;
(3)比值不带单位。
动手做一做:
(1)以下各组是四条线段的长,成比例线段的是( )
A. 4,8,3,5
B. 4,8,3,6
D. 8,4,1,3
C. 3,4,5,6
(2)已知线段a=2cm,b=3cm,c=6cm,且a、b、c、d成比例,则d= cm;若a、b、d、c成比例,则d= cm。
4
9
B
