生长数学视域下的特殊四边形十字架模型探究 课件 21张
文档属性
| 名称 | 生长数学视域下的特殊四边形十字架模型探究 课件 21张 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 21:18:33 | ||
图片预览






文档简介
(共21张PPT)
生长数学视域下的
特殊四边形十字架模型探究
教育即生长,生长本身就是目的。
——杜威
生长数学下复习课的内涵
生长数学下的复习课,基于生命视角重构数学教育价值,由生长源(元问题)出发,运用多维生长路径不断发现新问题,在问题解决过程中,形成核心知识间的关联与结构关系,归纳方法规律,领悟数学思想,积累活动经验,提升思维品质,实现生命成长。
复习不是知识、方法简单的重复,而是自主建构、不断知新、不断生长 过程。
1.生长性 所谓生长性,由生长源(元问题)出发,基于基础与经验,在解决问题过程中不断产生新问题,不断生长新的数学知识、方法、经验、思维。元问题可以是核心问题、基本图形,也可以是基本思想方法,具有根基性、生长性等特征。
2.结构性 知识结构性和整体性;教学的结构性,复习不是单一的“教师知识结构+中考试题”,而是“重建学生知识结构+师生创编(改编)的问题链;思维的结构性。
3.层次性 问题设计层次性;思维层次性(从低阶思维向高阶思维发展)。
生长数学下复习课的特征
特殊四边形中“十字架”模型的探究
案例:生长数学下复习课教学
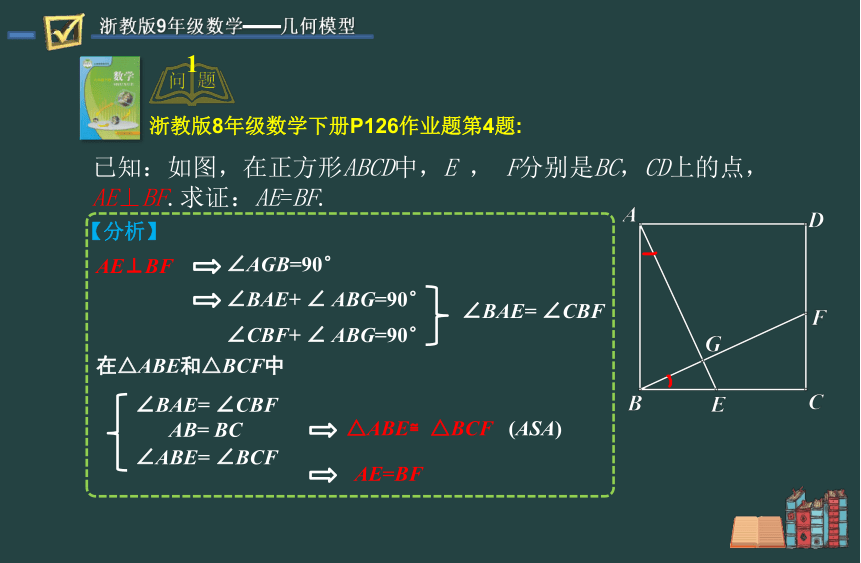
已知:如图,在正方形ABCD中,E , F分别是BC,CD上的点,AE⊥BF.求证:AE=BF.
浙教版9年级数学——几何模型
浙教版8年级数学下册P126作业题第4题:
问 题
【分析】
AE⊥BF
∠AGB=90°
∠BAE+ ∠ ABG=90°
∠CBF+ ∠ ABG=90°
∠BAE= ∠CBF
在△ABE和△BCF中
∠BAE= ∠CBF
AB= BC
∠ABE= ∠BCF
△ABE≌△BCF (ASA)
AE=BF
1
浙教版9年级数学——几何模型
变 式
1
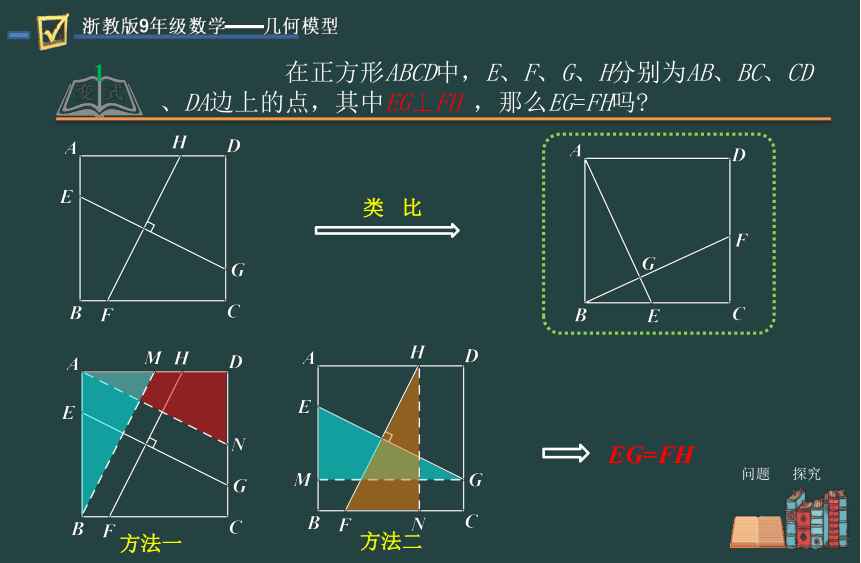
在正方形ABCD中,E、F、G、H分别为AB、BC、CD、DA边上的点,其中EG⊥FH ,那么EG=FH吗
EG=FH
类 比
方法一
方法二
问题 探究
浙教版9年级数学——几何模型
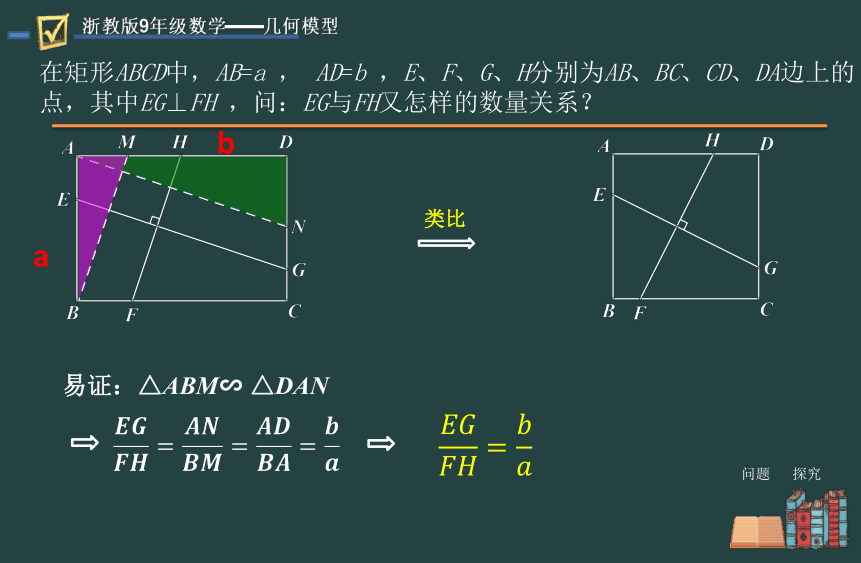
在矩形ABCD中,AB=a , AD=b ,E、F、G、H分别为AB、BC、CD、DA边上的点,其中EG⊥FH ,问:EG与FH又怎样的数量关系?
问题 探究
类比
易证:△ABM∽ △DAN
b
a
浙教版9年级数学——几何模型
1.如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的中点E处,折痕为FG ,点F、G分别在边AD,BC上,则折痕FG的长度为 .
2.如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的点E处,折痕为FG ,若FG的长为5,则线段CE的长为 .
连接AE,由轴对称的性质可得:FG⊥AE.
由十字架模型,易得:FG=AE
由十字架模型,易得:FG=AE
在Rt△ADE中,AE=FG=5 , AD=4
根据勾股定理:DE=3
所以,CE=4-DE=4-3=1
1
浙教版9年级数学——几何模型
根据折叠,我们可知:EF⊥BD.
由十字架模型,可得:
浙教版9年级数学——几何模型
问题 探究
如图,在Rt△ABC中,∠C=90°,AC=BC,D为BC的中点,CF⊥AD于E点,延长CE交AB于F ,则AF:FB= .
构造正方形AGBC
延长CF交BG于点H
十字架模型
△ACD≌△CBH
△ACF∽△BHF
2:1
例题1
浙教版9年级数学——几何模型
构造矩形BEDF
△ABE是等腰直角三角形
BE=AE=1
DE=AE+AD=1+2=3
浙教版9年级数学——几何模型
△ABC≌△ADC
△CDE∽△DAF
AF=
x
y
2x
2y
10
10
5
5
5+x=2y
2x+y=10
x=3
y=4
浙教版9年级数学——几何模型
十字架模型
AE=BF
构造模型
基本结论
模型应用
解题策略
知识 方法 经验
思维
生长型数学复习,关键找准生长源,形成生长链。它不只是数学知识的内部再生长,内容重构重组,也是思想方法经验积累式生长、学生思维的递进式生长,更是思维品质、生命品质的生长.
生长数学复习课堂的教学思考
1.生长,需要放慢节奏、静心等待
学生的思维处于形象思维为主的发展阶段,数学教学需要一个“慢”的过程。在教学中,教师应本着自然生长的心态,减少教学的浮躁与功利,“等一等”、“放一放”,留出独立思考的时间和空间,多一些自己探讨的经历和体会,多一些对知识的理解与提升,多一些与他人交流合作的机会和体验,多一些对思想方法的深思和顿悟,在数学课堂上慢慢生长,促进孩子自然生长。
生长数学复习课堂的教学思考
2.生长,需要理解宽容、真诚纳错
在新课程背景下,错误本身乃是“达到真理的一个必然的环节”(黑格尔语)。当课堂上学生出现差错时,教师的智慧不应是简单否定,或见弊就避,而应本着尊重、理解、欣赏、宽容的心态,直面学生的困惑,接纳学生的错误,帮助学生澄清困惑,让学生安全地、体面地、有尊严地矫正错误。
3.生长,需要完善学生的认知结构
知识的教学过程经历着从无到有、从小到大、从弱到强、从隐到明、从分到合的培育过程,在教学过程中,任何一个生长环节出现“裂痕”,都可能影响学生认知结构的形成和发展。
因此我们要从数学知识体系高度“结构化”的特点和学生认知结构的形成、发展规律出发,站在整体、系统和结构的高度把握和处理教材,在知识的联系中寻找交接点,巧妙地为高一层次的知识亮相蓄能造势。
4.生长,需要丰盈学生的活动体验
教师要引领学生用他自己的认知方式、思维方式去经历、体验、复演人类创造知识的生动历程,洞悉数学的本来面目,孕育数学的眼光和素养。在享受自己劳动成果的过程中,对数学学习产生一份积极的情感,其活动积累的体验会使学生获得学习数学、建构数学思想方法的后劲。
结 语
数学教学的主体是学生,学生的最大特性是“生长性”,如何让学生在知识生长、思维提升的过程中享受数学学习的乐趣,体验数学特有的魅力,激发自由创造的潜能,滋养数学内在的理性精神,需要教师的精铺巧设与智慧引领。
只要我们基于学生的发展需要,洞察学生的学习心理,循着寻求知识的真实轨迹行进,相信学生的生长一定是自然而有力的。
感谢倾听!
生长数学视域下的
特殊四边形十字架模型探究
教育即生长,生长本身就是目的。
——杜威
生长数学下复习课的内涵
生长数学下的复习课,基于生命视角重构数学教育价值,由生长源(元问题)出发,运用多维生长路径不断发现新问题,在问题解决过程中,形成核心知识间的关联与结构关系,归纳方法规律,领悟数学思想,积累活动经验,提升思维品质,实现生命成长。
复习不是知识、方法简单的重复,而是自主建构、不断知新、不断生长 过程。
1.生长性 所谓生长性,由生长源(元问题)出发,基于基础与经验,在解决问题过程中不断产生新问题,不断生长新的数学知识、方法、经验、思维。元问题可以是核心问题、基本图形,也可以是基本思想方法,具有根基性、生长性等特征。
2.结构性 知识结构性和整体性;教学的结构性,复习不是单一的“教师知识结构+中考试题”,而是“重建学生知识结构+师生创编(改编)的问题链;思维的结构性。
3.层次性 问题设计层次性;思维层次性(从低阶思维向高阶思维发展)。
生长数学下复习课的特征
特殊四边形中“十字架”模型的探究
案例:生长数学下复习课教学
已知:如图,在正方形ABCD中,E , F分别是BC,CD上的点,AE⊥BF.求证:AE=BF.
浙教版9年级数学——几何模型
浙教版8年级数学下册P126作业题第4题:
问 题
【分析】
AE⊥BF
∠AGB=90°
∠BAE+ ∠ ABG=90°
∠CBF+ ∠ ABG=90°
∠BAE= ∠CBF
在△ABE和△BCF中
∠BAE= ∠CBF
AB= BC
∠ABE= ∠BCF
△ABE≌△BCF (ASA)
AE=BF
1
浙教版9年级数学——几何模型
变 式
1
在正方形ABCD中,E、F、G、H分别为AB、BC、CD、DA边上的点,其中EG⊥FH ,那么EG=FH吗
EG=FH
类 比
方法一
方法二
问题 探究
浙教版9年级数学——几何模型
在矩形ABCD中,AB=a , AD=b ,E、F、G、H分别为AB、BC、CD、DA边上的点,其中EG⊥FH ,问:EG与FH又怎样的数量关系?
问题 探究
类比
易证:△ABM∽ △DAN
b
a
浙教版9年级数学——几何模型
1.如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的中点E处,折痕为FG ,点F、G分别在边AD,BC上,则折痕FG的长度为 .
2.如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的点E处,折痕为FG ,若FG的长为5,则线段CE的长为 .
连接AE,由轴对称的性质可得:FG⊥AE.
由十字架模型,易得:FG=AE
由十字架模型,易得:FG=AE
在Rt△ADE中,AE=FG=5 , AD=4
根据勾股定理:DE=3
所以,CE=4-DE=4-3=1
1
浙教版9年级数学——几何模型
根据折叠,我们可知:EF⊥BD.
由十字架模型,可得:
浙教版9年级数学——几何模型
问题 探究
如图,在Rt△ABC中,∠C=90°,AC=BC,D为BC的中点,CF⊥AD于E点,延长CE交AB于F ,则AF:FB= .
构造正方形AGBC
延长CF交BG于点H
十字架模型
△ACD≌△CBH
△ACF∽△BHF
2:1
例题1
浙教版9年级数学——几何模型
构造矩形BEDF
△ABE是等腰直角三角形
BE=AE=1
DE=AE+AD=1+2=3
浙教版9年级数学——几何模型
△ABC≌△ADC
△CDE∽△DAF
AF=
x
y
2x
2y
10
10
5
5
5+x=2y
2x+y=10
x=3
y=4
浙教版9年级数学——几何模型
十字架模型
AE=BF
构造模型
基本结论
模型应用
解题策略
知识 方法 经验
思维
生长型数学复习,关键找准生长源,形成生长链。它不只是数学知识的内部再生长,内容重构重组,也是思想方法经验积累式生长、学生思维的递进式生长,更是思维品质、生命品质的生长.
生长数学复习课堂的教学思考
1.生长,需要放慢节奏、静心等待
学生的思维处于形象思维为主的发展阶段,数学教学需要一个“慢”的过程。在教学中,教师应本着自然生长的心态,减少教学的浮躁与功利,“等一等”、“放一放”,留出独立思考的时间和空间,多一些自己探讨的经历和体会,多一些对知识的理解与提升,多一些与他人交流合作的机会和体验,多一些对思想方法的深思和顿悟,在数学课堂上慢慢生长,促进孩子自然生长。
生长数学复习课堂的教学思考
2.生长,需要理解宽容、真诚纳错
在新课程背景下,错误本身乃是“达到真理的一个必然的环节”(黑格尔语)。当课堂上学生出现差错时,教师的智慧不应是简单否定,或见弊就避,而应本着尊重、理解、欣赏、宽容的心态,直面学生的困惑,接纳学生的错误,帮助学生澄清困惑,让学生安全地、体面地、有尊严地矫正错误。
3.生长,需要完善学生的认知结构
知识的教学过程经历着从无到有、从小到大、从弱到强、从隐到明、从分到合的培育过程,在教学过程中,任何一个生长环节出现“裂痕”,都可能影响学生认知结构的形成和发展。
因此我们要从数学知识体系高度“结构化”的特点和学生认知结构的形成、发展规律出发,站在整体、系统和结构的高度把握和处理教材,在知识的联系中寻找交接点,巧妙地为高一层次的知识亮相蓄能造势。
4.生长,需要丰盈学生的活动体验
教师要引领学生用他自己的认知方式、思维方式去经历、体验、复演人类创造知识的生动历程,洞悉数学的本来面目,孕育数学的眼光和素养。在享受自己劳动成果的过程中,对数学学习产生一份积极的情感,其活动积累的体验会使学生获得学习数学、建构数学思想方法的后劲。
结 语
数学教学的主体是学生,学生的最大特性是“生长性”,如何让学生在知识生长、思维提升的过程中享受数学学习的乐趣,体验数学特有的魅力,激发自由创造的潜能,滋养数学内在的理性精神,需要教师的精铺巧设与智慧引领。
只要我们基于学生的发展需要,洞察学生的学习心理,循着寻求知识的真实轨迹行进,相信学生的生长一定是自然而有力的。
感谢倾听!
同课章节目录
