探究辅助圆的基本模型 课件16张

(共16张PPT)
探究辅助圆的基本模型
初三第二轮专题复习课
情境引入
球 门
A1
M
N
A2
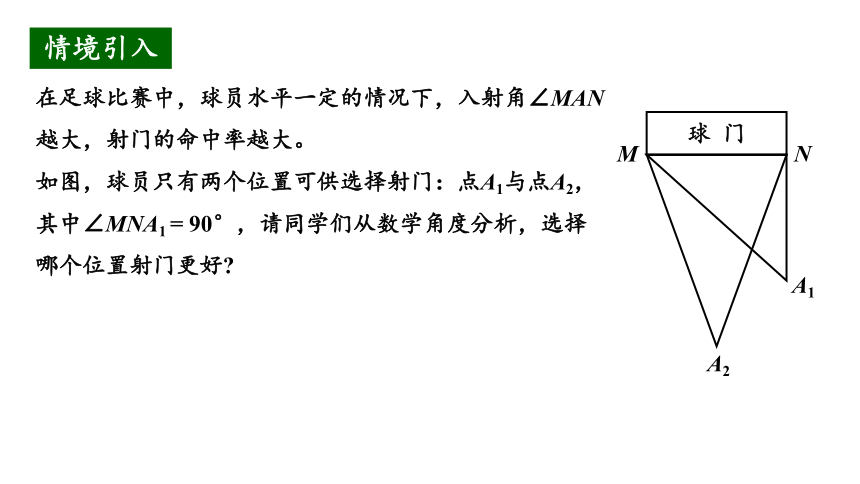
在足球比赛中，球员水平一定的情况下，入射角∠MAN越大，射门的命中率越大。
如图，球员只有两个位置可供选择射门：点A1与点A2，其中∠MNA1 = 90°，请同学们从数学角度分析，选择哪个位置射门更好
模型探究
探究1.
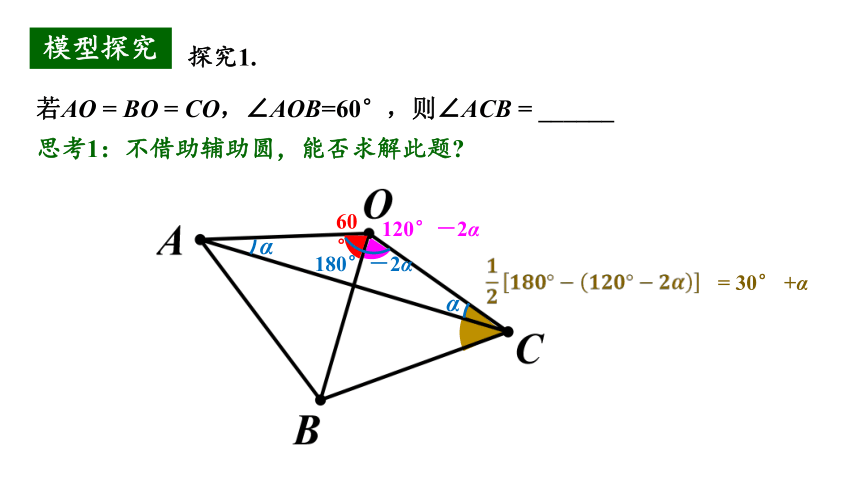
若AO = BO = CO，∠AOB=60°，则∠ACB = ______
思考1：不借助辅助圆，能否求解此题
60°
α
α
180°－2α
120°－2α
= 30° +α
模型探究
探究1.
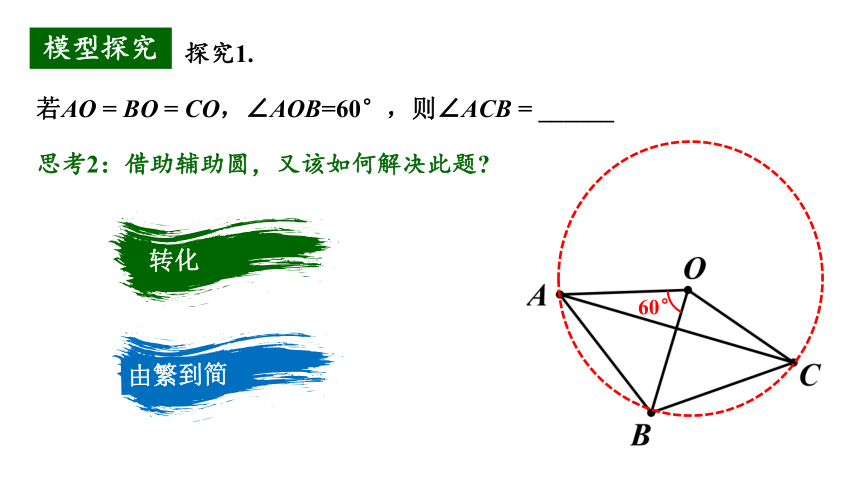
若AO = BO = CO，∠AOB=60°，则∠ACB = ______
思考2：借助辅助圆，又该如何解决此题
60°
转化
由繁到简
模型应用
1. 如图，△PAC为等边三角形，点A，点B关于直线l对称，其中点A，点B在x轴上，点C在y轴上，点P在直线l上，求线段OC和线段OB的数量关系
模型探究
探究2.
已知点C为线段AB外一动点，∠ACB=90°，AB=2，动点C在运动过程中所经过的路径是什么 如何画图
.
O
模型应用
2.如图，在正方形ABCD中，AB=2，点E，F分别为边DC，CB上的点，且始终保持DE=CF，连接AE和DF交于点P，求线段CP的最小值
.
O
P’
.
1
2
小组活动
活动1：已知点C为定线段AB上方的动点，∠ACB=80°，探究动点C的运动路径
活动2：已知点D为定线段AB下方的动点，∠ADB=100°，探究动点D的运动路径
C
A
B
D
A
B
图1
图2
探究3.
O
3. 如图，点A(2，0)，点B(6，0)，点P为x轴上方的动点， ∠APB=60°，
求点P的运动路径的长度
模型应用
.
H
O
240°
模型归纳
在以上的探究活动中，图形虽没有“圆”，但在探究过程中却用到“圆”
像这样，根据条件构造出“圆”的问题，称为“辅助圆问题”
复杂问题
简单问题
数学建模
基本图形
1审题
已知信息
2标注
辅助线
3添加
解题步骤
基本模型
4判断
模型归纳
情境再现
球 门
A1
M
N
A2
.
O
.
B
在足球比赛中，球员水平一定的情况下，入射角∠MAN越大，射门的命中率越大。
如图，球员只有两个位置可供选择射门：点A1与点A2，其中∠MNA1 = 90°，请同学们从数学角度分析，选择哪个位置射门更好
知
识
点
辅助圆模型
数学思想
数学建模
转化
课堂小结
由繁到简
聚焦中考
2021年湖州第9题
如图，已知在矩形ABCD中，AB = 1，BC = ，点P是AD边上的一个动点，连结BP，点C关于直线BP的对称点为C’，当点P运动时，点C’也随之运动，若点P从点A运动到点D，则线段CC’扫过的区域的面积是( )
A. π B. C. D.2π
波利亚（George Polya）
数学典故
“如果你希望从自己的努力中，取得最大的收获，就要从已经解决的问题中找出那些对处理将来问题可能有用的特征。”