人教版数学九年级下册第二十八章——解直角三角形及其应用 课件30张
文档属性
| 名称 | 人教版数学九年级下册第二十八章——解直角三角形及其应用 课件30张 |  | |
| 格式 | pptx | ||
| 文件大小 | 26.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 21:27:57 | ||
图片预览










文档简介
(共30张PPT)
核心素养视野下的数学教学研究
——解直角三角形及其应用
人教版数学九年级下册第三单元异步教研
目录
CONTENTS
一
二
三
数学核心素养理念的解读
解直角三角形中的核心素养
在课堂中如何落实核心素养
数学核心素养
理念的解读
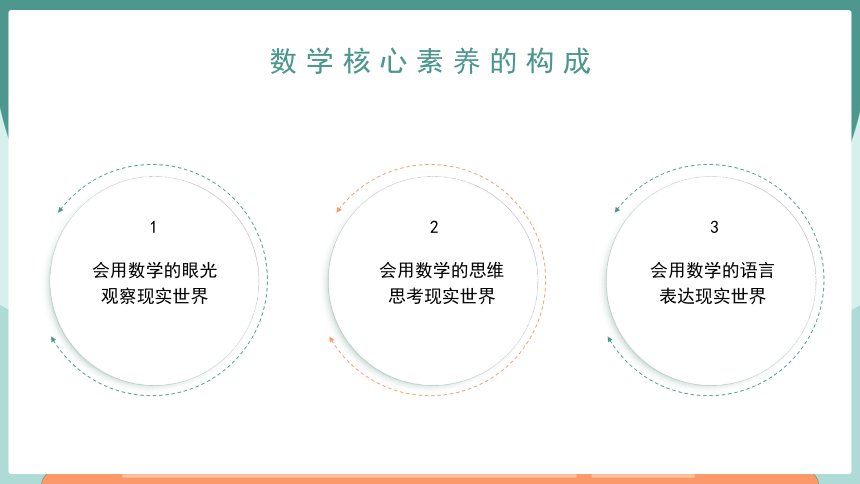
数学核心素养的构成
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
1
2
3
数学核心素养的主要表现
数学核心素养具有整体性、一致性和阶段性,初中阶段侧重对概念的理解。
数学眼光
数学思维
数学语言
培养学生数学抽象能力,体现了数学的一般性特征。
培养学生数学逻辑推理能力,体现了数学的严谨性特征。
是让学生建立数学模型,体现了数学应用广泛性特征。
数学核心素养的主要表现
小学11个关键词:
数学眼光:符号意识、数感、量感、 几何直观、空间观念、创新意识;
数学思维:推理意识、运算能力;
数学语言:模型意识、数据意识、应用意识
数学眼光:抽象能力、几何直观、空间观念、创新意识;
数学思维:推理能力、运算能力;
数学语言:模型观念、数据观念、应用意识
初中9个关键词:
A
B
C
A
B
C
《解直角三角形》中核心素养解读
新课标中提出的要求
【内容要求】
1、利用相似的直角三角形,探索并认识锐角三角函数(sin A,cos A,tan A),知道30, 45, 60角的三角函数值。
2、会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它的对应锐角
3、能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题
【学业要求】
1、在直观理解和掌握图形与几何基本事实的基础上,经历得到和验证数学结论的过程,感悟具有传递性的数学逻辑,形成几何直观和推理能力。
2、知道直角三角形的边角关系,理解锐角三角函数,能用锐角三角函数解决简单的实际问题。
3、在具体现实情境中,学会从几何的角度发现问题和提出问题,经历用几何直观和逻辑推理分析问题和解决问题的过程,培养应用意识和创新意识,提升几何直观、空间观念、抽象能力、推理能力等。
数学的眼光观察现实世界—几何直观/抽象能力
几何直观
学生要能够感知各种几何图形及其组成元素,依据图形的特征进行分类;能够建立形与数的联系,构建数学问题的直观模型;利用图表分析实际情境与数学问题,探索解决问题的思路。在解直角三角形中,学生需要学会分析实际情境,寻找直角三角形解决问题。
抽象能力
学生需要能够根据物体特征抽象出几何图形,根据几何图形想像出所描述的实际物体。空间观念有助于学生理解现实生活中空间物体的形态与结构,是形成空间想象力的经验基础。解直角三角形中的题目类型多数为现实生活中的实际问题,学生需要学会从实际问题抽象出几何图形。
数学的眼光观察现实世界—几何直观/抽象能力
在本单元的引言中已经体现出学生所需的核心素养,本单元需要学生能够结合数与形之间的关系,分析实际情境,解决实际问题。
数学的思维思考现实世界—推理能力
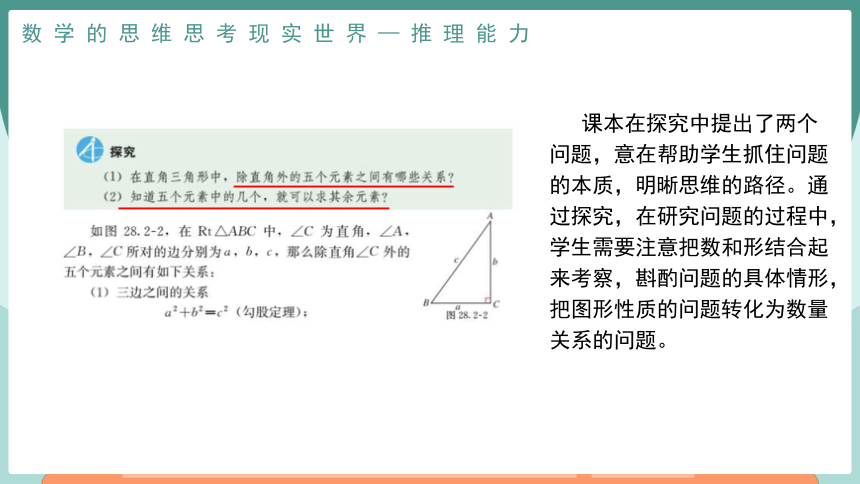
推理能力
推理能力主要是指从一些事实和命题出发,依据规则推出其他命题或结论的能力。学生需要理解逻辑推理在形成数学概念、法则、定理和解决问题中的重要性;需要理解命题的结构与联系,探索并表述论证过程。
课本在探究中提出了两个问题,意在帮助学生抓住问题的本质,明晰思维的路径。通过探究,在研究问题的过程中,学生需要注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题。
数学的思维思考现实世界—推理能力
数学的思维思考现实世界—推理能力
在例题后,课本归纳总结出了利用解直角三角形的知识解决实际问题的一般过程,引导学生从具体的问题解决中概括出一般结论,形成数学的方法和策略,经历数学“再发现”过程,发展质疑问难的批判性思维。
结合
数学的思维思考现实世界—推理能力
数学的语言表达现实世界—模型观念/应用意识
模型观念
模型观念主要是指对运用数学模型解决实际问题有清晰的认识。对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题。在解直角三角形中,学生需要学会从具体情境中抽象出数学模型,感悟数学应用的普遍性。
应用意识
应用意识主要指有意识地利用数学的概念、原理、和方法解释现实世界中的现象和规律,解决现实世界中的问题。学生需要能够感悟现实生活中蕴含着大量的与数量和图形有关的问题,可以用数学的方法予以解决。
数学的语言表达现实世界—模型观念/应用意识
课本中给出了三个与生活相关的例题,都是从实际问题中抽象出数学模型进行解决,归结为建立直角三角形模型问题。学生需要能够从实际情境中抽象出核心变量、变量的规律及变量之间的关系。
数学的语言表达现实世界—模型观念/应用意识
在课堂中如何培养核心素养
教学导语:同学们,在本章引言中提出了关于比萨斜塔的问题,我们已经学习了锐角三角函数的相关知识,现在你能利用已有知识解决这个问题了吗?你能发现什么?
【设计意图】帮助学生在回顾前一节知识的同时,和本节课的相关知识建立通道。从问题中的指向捕捉真正有价值的内容,引导数学的思考,培育学生的理性思维和抽象能力。
在课堂中如何培养核心素养
A
B
C
师:将上述问题推广到一般情形,就是:已知直角三角形的斜边和一条直角边,求它的锐角的度数。那么在直角三角形中知道几个条件可以求解呢?
【设计意图】重视发散性问题的归纳,培育学生理性思维。学生面对发散性问题时,需要找到它的数学视角才能全面、准确地回答该问题。此时学生作答后教师的提炼能帮助学生看到问题的数学本质,从问题指向中捕捉真正有价值的内容,引导数学的思考,培育学生的理性思维。
(预设)学生可以说出其中几种答案,但是无法有效归类,教师归纳学生发言后,从角到边带领学生总结:
1、知道一个角(不能)
2、知道两个角(不能)
3、知道一角一边(可以)
4、知道两边(可以)
师:从以上探究过程中可以发现在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
在课堂中如何培养核心素养
在课堂中如何培养核心素养
(1)如何引导学生从实际情景中提出和发现问题.
(2)如何引导学生从实际问题中抽象、简化或结构化建立合理的数学模型.
(3)弧PQ 长与哪些量有关,如何启发学生求弧PQ 长转化为解直角三角形
(4)如何真正地实现数学建模的意义
在课堂中如何培养核心素养
【设计意图】在问题中仅呈现图(1),不给出其它的图示,目的是创造真实的情境,让学生经历抽象、概括和符号化、简约化的过程.如问题中2用抽象的眼光看,地球抽象成球,飞船抽象成点,得到图(2).结合题意用数学符号语言简约化的描述,飞船用点A表示,飞船离地球最近的点为 B,飞船能看到地球最远的点C,用圆弧表示最近点与最远点的距离,得到图(3).求弧BC的长关键是求∠θ,从而转化为图(4)解 Rt△AOC.
在课堂中如何培养核心素养
课本所给的三道例题,其基本核心解决方法都是作垂线,并且模型基本相似,可以总结出几个其他的模型,帮助学生拓展思路,解决更多的实际问题,借此培养学生的抽象能力与模型观念
在课堂中如何培养核心素养
【设计意图】课堂上突破难点时,通常通过一个问题的解决难以达到目的,所以教师通过类似问题数量的增加、已有问题的变式、探究视角的深入等方式设置问题串,逐步揭示研究对象的本质。
师:同学们在完成了这三道例题后,从总体的角度来分析,你有发现什么吗?从数学模型的角度,你有什么收获吗?你又可以从中提出什么变式吗?
引导学生在两种模型的基础上拓展思维,寻找更多的模型,并引导学生归纳出这类模型的破题思路,培养学生的抽象能力和模型观念
共边异侧双直角三角形
共边同侧双直角三角形
平移
平移
……
平移
平移
……
在课堂中如何培养核心素养
在课堂中如何培养核心素养
教材上的很多练习都是经典问题,也是“重要习题”。各级各类考试命题时往往都强调要“回归教材”,这就出现了很多考题需要从教材例题、习题中找到原型或“影子”,这就引导教师要重视教材习题的教学运用。而教材中的问题又给学生提供了新的模型,教师可以让学生模仿前面的归纳过程,自行去试一试归纳模型。
如图,在电线杆上的C处引拉线CE,CF固定电线杆. 拉线CE和地面成60°角,在离电线杆6米的A处测得AC与水平面的夹角为30°,已知A与地面的距离为1.5米,求拉线CE的长.(结果保留根号)
变式举例
如图,某防洪指挥部发现长江边一处防洪大堤 (横断面为梯形ABCD) 急需加固,背水坡的坡角为45°,高10米.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽 2米,加固后背水坡EF的坡比 .求加固后坝底增加的宽度AF. (结果保留根号)
A
B
C
D
E
F
45°
在课堂中如何培养核心素养
【设计意图】教师引导、调整学生探究方向与难度,学生尝试逐步深入分析,对分析得到的信息加工处理。在这样的过程中,学生的问题意识增强,分析问题、解决问题的能力增强,特别是在积极主动的探索与思考中,学生的创新意识 、应用意识在具体情境中被激发。
解直角三角形实际应用题的常见图形类型及辅助线作法
在课堂中如何培养核心素养
目前,大多数问题都来源于日常生活,而生活化的背景可以让学生学会将问题建模,抽象出问题本质,解决问题。
在课堂中如何培养核心素养
问题是数学的心脏,在问题的解决过程中,不仅让学生获得“四基”“四能”,而且在探索实践中发展学生的数学核心素养,体现“教师是培养数学核心素养的主体,课堂是培养数学核心素养的主渠道 ” 。因此,教师应该以问题为载体,以学生深度理解概念为显性目标,优化对问题的处理,最终达成提升学生数学核心素养的终极目标。
教研共同体浙江张宗余名师团队
谢谢倾听
核心素养视野下的数学教学研究
——解直角三角形及其应用
人教版数学九年级下册第三单元异步教研
目录
CONTENTS
一
二
三
数学核心素养理念的解读
解直角三角形中的核心素养
在课堂中如何落实核心素养
数学核心素养
理念的解读
数学核心素养的构成
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
1
2
3
数学核心素养的主要表现
数学核心素养具有整体性、一致性和阶段性,初中阶段侧重对概念的理解。
数学眼光
数学思维
数学语言
培养学生数学抽象能力,体现了数学的一般性特征。
培养学生数学逻辑推理能力,体现了数学的严谨性特征。
是让学生建立数学模型,体现了数学应用广泛性特征。
数学核心素养的主要表现
小学11个关键词:
数学眼光:符号意识、数感、量感、 几何直观、空间观念、创新意识;
数学思维:推理意识、运算能力;
数学语言:模型意识、数据意识、应用意识
数学眼光:抽象能力、几何直观、空间观念、创新意识;
数学思维:推理能力、运算能力;
数学语言:模型观念、数据观念、应用意识
初中9个关键词:
A
B
C
A
B
C
《解直角三角形》中核心素养解读
新课标中提出的要求
【内容要求】
1、利用相似的直角三角形,探索并认识锐角三角函数(sin A,cos A,tan A),知道30, 45, 60角的三角函数值。
2、会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它的对应锐角
3、能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题
【学业要求】
1、在直观理解和掌握图形与几何基本事实的基础上,经历得到和验证数学结论的过程,感悟具有传递性的数学逻辑,形成几何直观和推理能力。
2、知道直角三角形的边角关系,理解锐角三角函数,能用锐角三角函数解决简单的实际问题。
3、在具体现实情境中,学会从几何的角度发现问题和提出问题,经历用几何直观和逻辑推理分析问题和解决问题的过程,培养应用意识和创新意识,提升几何直观、空间观念、抽象能力、推理能力等。
数学的眼光观察现实世界—几何直观/抽象能力
几何直观
学生要能够感知各种几何图形及其组成元素,依据图形的特征进行分类;能够建立形与数的联系,构建数学问题的直观模型;利用图表分析实际情境与数学问题,探索解决问题的思路。在解直角三角形中,学生需要学会分析实际情境,寻找直角三角形解决问题。
抽象能力
学生需要能够根据物体特征抽象出几何图形,根据几何图形想像出所描述的实际物体。空间观念有助于学生理解现实生活中空间物体的形态与结构,是形成空间想象力的经验基础。解直角三角形中的题目类型多数为现实生活中的实际问题,学生需要学会从实际问题抽象出几何图形。
数学的眼光观察现实世界—几何直观/抽象能力
在本单元的引言中已经体现出学生所需的核心素养,本单元需要学生能够结合数与形之间的关系,分析实际情境,解决实际问题。
数学的思维思考现实世界—推理能力
推理能力
推理能力主要是指从一些事实和命题出发,依据规则推出其他命题或结论的能力。学生需要理解逻辑推理在形成数学概念、法则、定理和解决问题中的重要性;需要理解命题的结构与联系,探索并表述论证过程。
课本在探究中提出了两个问题,意在帮助学生抓住问题的本质,明晰思维的路径。通过探究,在研究问题的过程中,学生需要注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题。
数学的思维思考现实世界—推理能力
数学的思维思考现实世界—推理能力
在例题后,课本归纳总结出了利用解直角三角形的知识解决实际问题的一般过程,引导学生从具体的问题解决中概括出一般结论,形成数学的方法和策略,经历数学“再发现”过程,发展质疑问难的批判性思维。
结合
数学的思维思考现实世界—推理能力
数学的语言表达现实世界—模型观念/应用意识
模型观念
模型观念主要是指对运用数学模型解决实际问题有清晰的认识。对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题。在解直角三角形中,学生需要学会从具体情境中抽象出数学模型,感悟数学应用的普遍性。
应用意识
应用意识主要指有意识地利用数学的概念、原理、和方法解释现实世界中的现象和规律,解决现实世界中的问题。学生需要能够感悟现实生活中蕴含着大量的与数量和图形有关的问题,可以用数学的方法予以解决。
数学的语言表达现实世界—模型观念/应用意识
课本中给出了三个与生活相关的例题,都是从实际问题中抽象出数学模型进行解决,归结为建立直角三角形模型问题。学生需要能够从实际情境中抽象出核心变量、变量的规律及变量之间的关系。
数学的语言表达现实世界—模型观念/应用意识
在课堂中如何培养核心素养
教学导语:同学们,在本章引言中提出了关于比萨斜塔的问题,我们已经学习了锐角三角函数的相关知识,现在你能利用已有知识解决这个问题了吗?你能发现什么?
【设计意图】帮助学生在回顾前一节知识的同时,和本节课的相关知识建立通道。从问题中的指向捕捉真正有价值的内容,引导数学的思考,培育学生的理性思维和抽象能力。
在课堂中如何培养核心素养
A
B
C
师:将上述问题推广到一般情形,就是:已知直角三角形的斜边和一条直角边,求它的锐角的度数。那么在直角三角形中知道几个条件可以求解呢?
【设计意图】重视发散性问题的归纳,培育学生理性思维。学生面对发散性问题时,需要找到它的数学视角才能全面、准确地回答该问题。此时学生作答后教师的提炼能帮助学生看到问题的数学本质,从问题指向中捕捉真正有价值的内容,引导数学的思考,培育学生的理性思维。
(预设)学生可以说出其中几种答案,但是无法有效归类,教师归纳学生发言后,从角到边带领学生总结:
1、知道一个角(不能)
2、知道两个角(不能)
3、知道一角一边(可以)
4、知道两边(可以)
师:从以上探究过程中可以发现在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
在课堂中如何培养核心素养
在课堂中如何培养核心素养
(1)如何引导学生从实际情景中提出和发现问题.
(2)如何引导学生从实际问题中抽象、简化或结构化建立合理的数学模型.
(3)弧PQ 长与哪些量有关,如何启发学生求弧PQ 长转化为解直角三角形
(4)如何真正地实现数学建模的意义
在课堂中如何培养核心素养
【设计意图】在问题中仅呈现图(1),不给出其它的图示,目的是创造真实的情境,让学生经历抽象、概括和符号化、简约化的过程.如问题中2用抽象的眼光看,地球抽象成球,飞船抽象成点,得到图(2).结合题意用数学符号语言简约化的描述,飞船用点A表示,飞船离地球最近的点为 B,飞船能看到地球最远的点C,用圆弧表示最近点与最远点的距离,得到图(3).求弧BC的长关键是求∠θ,从而转化为图(4)解 Rt△AOC.
在课堂中如何培养核心素养
课本所给的三道例题,其基本核心解决方法都是作垂线,并且模型基本相似,可以总结出几个其他的模型,帮助学生拓展思路,解决更多的实际问题,借此培养学生的抽象能力与模型观念
在课堂中如何培养核心素养
【设计意图】课堂上突破难点时,通常通过一个问题的解决难以达到目的,所以教师通过类似问题数量的增加、已有问题的变式、探究视角的深入等方式设置问题串,逐步揭示研究对象的本质。
师:同学们在完成了这三道例题后,从总体的角度来分析,你有发现什么吗?从数学模型的角度,你有什么收获吗?你又可以从中提出什么变式吗?
引导学生在两种模型的基础上拓展思维,寻找更多的模型,并引导学生归纳出这类模型的破题思路,培养学生的抽象能力和模型观念
共边异侧双直角三角形
共边同侧双直角三角形
平移
平移
……
平移
平移
……
在课堂中如何培养核心素养
在课堂中如何培养核心素养
教材上的很多练习都是经典问题,也是“重要习题”。各级各类考试命题时往往都强调要“回归教材”,这就出现了很多考题需要从教材例题、习题中找到原型或“影子”,这就引导教师要重视教材习题的教学运用。而教材中的问题又给学生提供了新的模型,教师可以让学生模仿前面的归纳过程,自行去试一试归纳模型。
如图,在电线杆上的C处引拉线CE,CF固定电线杆. 拉线CE和地面成60°角,在离电线杆6米的A处测得AC与水平面的夹角为30°,已知A与地面的距离为1.5米,求拉线CE的长.(结果保留根号)
变式举例
如图,某防洪指挥部发现长江边一处防洪大堤 (横断面为梯形ABCD) 急需加固,背水坡的坡角为45°,高10米.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽 2米,加固后背水坡EF的坡比 .求加固后坝底增加的宽度AF. (结果保留根号)
A
B
C
D
E
F
45°
在课堂中如何培养核心素养
【设计意图】教师引导、调整学生探究方向与难度,学生尝试逐步深入分析,对分析得到的信息加工处理。在这样的过程中,学生的问题意识增强,分析问题、解决问题的能力增强,特别是在积极主动的探索与思考中,学生的创新意识 、应用意识在具体情境中被激发。
解直角三角形实际应用题的常见图形类型及辅助线作法
在课堂中如何培养核心素养
目前,大多数问题都来源于日常生活,而生活化的背景可以让学生学会将问题建模,抽象出问题本质,解决问题。
在课堂中如何培养核心素养
问题是数学的心脏,在问题的解决过程中,不仅让学生获得“四基”“四能”,而且在探索实践中发展学生的数学核心素养,体现“教师是培养数学核心素养的主体,课堂是培养数学核心素养的主渠道 ” 。因此,教师应该以问题为载体,以学生深度理解概念为显性目标,优化对问题的处理,最终达成提升学生数学核心素养的终极目标。
教研共同体浙江张宗余名师团队
谢谢倾听
