4.5相似三角形判定定理的证明同步练习(含答案) 2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 4.5相似三角形判定定理的证明同步练习(含答案) 2024-2025学年北师大版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 371.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
*5相似三角形判定定理的证明
基础题目
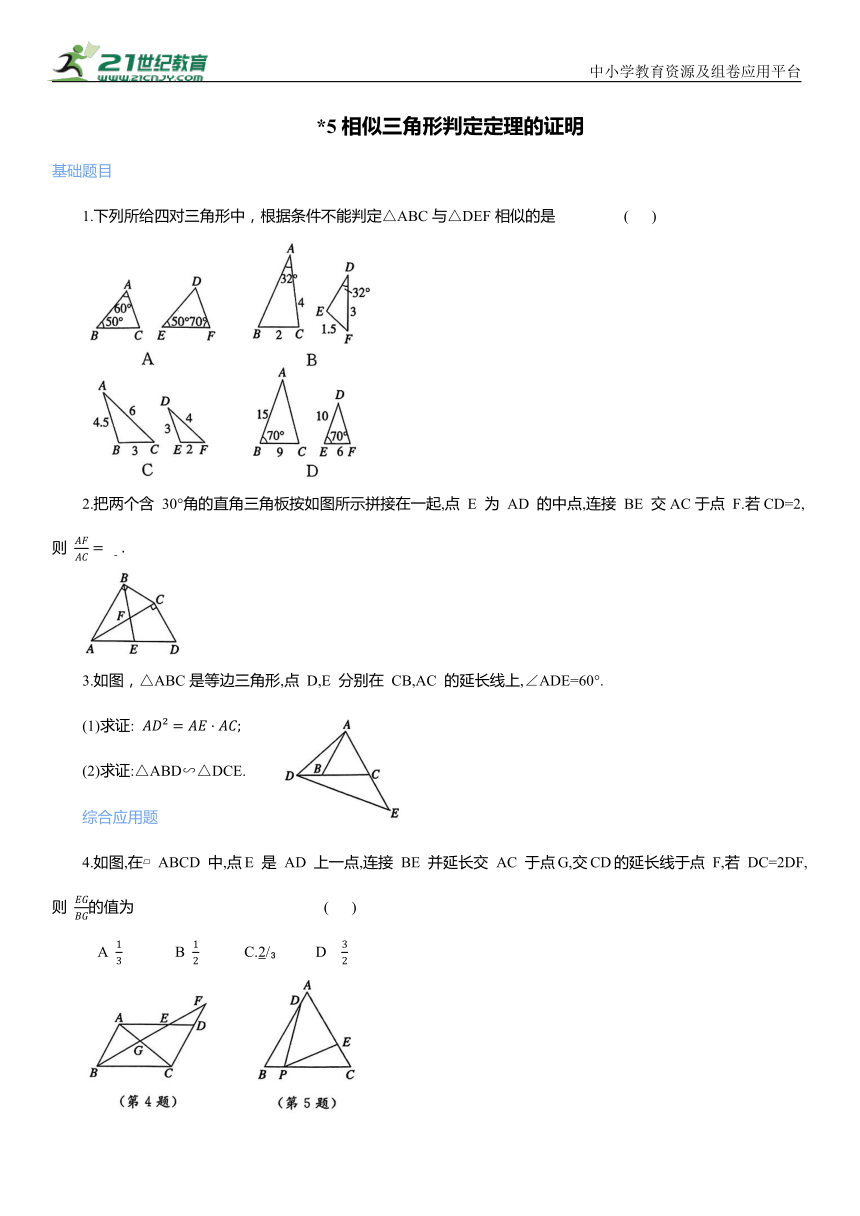
1.下列所给四对三角形中,根据条件不能判定△ABC与△DEF相似的是 ( )
2.把两个含 30°角的直角三角板按如图所示拼接在一起,点 E 为 AD 的中点,连接 BE 交AC于点 F.若CD=2,则
3.如图,△ABC是等边三角形,点 D,E 分别在 CB,AC 的延长线上,∠ADE=60°.
(1)求证:
(2)求证:△ABD∽△DCE.
综合应用题
4.如图,在 ABCD 中,点E 是 AD 上一点,连接 BE 并延长交 AC 于点G,交CD的延长线于点 F,若 DC=2DF,则 的值为 ( )
A B C.2/ D
5.如图,△ABC 是边长为7 cm的等边三角形,BD=6 cm,CE=2 cm,P 为 BC上的动点,以 0.25 cm/s的速度从 B向C运动,假设 P 点运动的时间为t s,当t= 时,△BDP 与△CPE相似.
6如图,四边形ABCD为平行四边形,E为边 AD 上一点,连接 AC,BE,它们相交于点 F,且∠ACB=∠ABE.
(1)求证:
(2)若AE=2,EF=1,CF=4,求AB的长.
7(1)如图①,在 Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为 D,求AD的长.
(2)如图②,△ABC中,AC=14,BC=6,点 D,E分别在线段AB,AC 上,∠EDB=∠ACB=60°,DE=2,求AD 的长.
创新拓展题
8.【问题探究】
课外兴趣小组活动时,同学们在解决如下问题:如图①,在矩形 ABCD中,点 E,F 分别是边DC,BC上的点,连接AE,DF,且AE⊥DF 于点G,若AB=6,BC=8,求 的值.
(1)请你帮助同学们解决上述问题.
【初步运用】
(2)如图②,在△ABC中, 点 D 为AC的中点,连接 BD,过点 A 作 AE⊥BD于点E,交BC于点 F,求 的值.
【灵活运用】
(3)如图③,在四边形 ABCD 中,∠BAD=90°, 点 E,F 分别在边AB,AD 上,且 DE⊥CF,垂足为 G,则
*5相似三角形判定定理的证明
1. B
2 【点拨】如图,连接CE
∵∠CAD=30°,∠ACD=90°,E是AD的中点,
易得
∴∠ACE=∠CAE=30°.
∵∠BAC=30°,∠ABC=90°,
∴∠BAC=∠ACE,易得
∴AB∥CE.∴∠ABF=∠CEF.∴△ABF∽△CEF.
3.【证明】(1)∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ADE=60°,∴∠ADE=∠ACB.
又∵∠DAC=∠EAD,
∴△ACD∽△ADE.
(2)由(1)得△ACD∽△ADE,∴∠ADC=∠E.
∵△ABC是等边三角形,∴∠ACD=∠ABC=60°.
∴∠ABD=∠ECD=120°.
又∵∠ADB=∠E,
∴△ABD∽△DCE.
4. C 【点拨】∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC.∴∠FED=∠FBC,∠FDE=∠FCB.
∴△DEF∽△CBF.
··器=ぴ.∵DC=2DF,∴CF=3DF.
‥器 .‥器 .∵AD∥BC,∴∠GAE=∠GCB∠GEA=∠GBC.
故选 C.
5.12 或 16 或 21 【点拨】易得∠B=∠C.若△BDP∽△CPE,则 或4 cm. 或
若△BDP∽△CEP,则
综上所述,当t=12 或 16 或 21 时,△BDP 与△CPE相似.
6.(1)【证明】∵四边形ABCD为平行四边形,
∴AD∥BC.
∴∠DAC=∠ACB.
又∵∠ACB=∠ABE,
∴∠DAC=∠ABE.
又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
∴EA: EB=EF: EA.
(2)【解】
∴BF=BE-EF=4-1=3.
∵AE∥BC,
即 解得
∵△EAF∽△EBA,
即
7.【解】(1)∵ED⊥AB,∴∠ADE=90°=∠C.
又∵∠A=∠A,
∵AB=10,AC=8,AE=5,
解得AD=4.
(2)在AC上截取CH=CB,连接BH.
∵∠ACB=60°,
∴△BCH为等边三角形.
∴CH=BH=BC=6,∠CHB=60°.
∴AH=AC-CH=8,∠AHB=120°.
∵∠EDB=60°,
∴∠ADE=120°.∴∠ADE=∠AHB.
又∵∠A=∠A,
∴△ADE∽△AHB.∴BB=AB,即 解得
8.【解】(1)∵AE⊥DF,∴∠EGD=90°.
∴∠EDG+∠DEG=90°.
∵四边形ABCD为矩形,
∴AB=CD=6,BC=AD=8,∠C=∠ADE=90°.
∴∠EDG+∠DFC=90°.∴∠DEG=∠DFC.
(2)构造如图①所示矩形ABHC,延长AF交CH 于点G,由(1)中结论可得△ABD∽△CAG.
∴设AB=3k,AC=4k.
∵点 D为AC 的中点,
在 Rt△ABD中,根据勾股定理可得
∵△ABD∽△CAG,
则 解得
∵四边形ABHC为矩形,∴AB∥CG.
∴∠BAF=∠CGF,∠ABF=∠GCF.
∴△ABF∽△GCF.
即
解得
(3 【点拨】连接 BD,构造如图②所示的矩形AMND过点 N作NP∥CF,交AD于点P,连接 BD.
∵AB=BC,AD=CD,BD=BD,
∴△ABD≌△CBD.
∴∠BCD=∠A=90°.
∴∠BCM+∠DCN=90°.
∵四边形 AMND 为矩形,
∴MN=AD,DN=AM,AD∥MN,∠M=∠MND=90°.
∴∠BCM+∠CBM=90°,∴∠DCN=∠CBM.
又∵∠M=∠CND=90°,∴△DCN∽△CBM.
∴设AB=BC=3k,AD=CD=4k.
设 BM=3x,CN=4x,
则CM=MN-CN=AD-CN=4k-4x,DN=AM=AB+BM=3k+3x,
整理得
由(1)中结论可得
∵NP∥CF,CN∥PF,
∴四边形 FCNP 为平行四边形,
*5相似三角形判定定理的证明
基础题目
1.下列所给四对三角形中,根据条件不能判定△ABC与△DEF相似的是 ( )
2.把两个含 30°角的直角三角板按如图所示拼接在一起,点 E 为 AD 的中点,连接 BE 交AC于点 F.若CD=2,则
3.如图,△ABC是等边三角形,点 D,E 分别在 CB,AC 的延长线上,∠ADE=60°.
(1)求证:
(2)求证:△ABD∽△DCE.
综合应用题
4.如图,在 ABCD 中,点E 是 AD 上一点,连接 BE 并延长交 AC 于点G,交CD的延长线于点 F,若 DC=2DF,则 的值为 ( )
A B C.2/ D
5.如图,△ABC 是边长为7 cm的等边三角形,BD=6 cm,CE=2 cm,P 为 BC上的动点,以 0.25 cm/s的速度从 B向C运动,假设 P 点运动的时间为t s,当t= 时,△BDP 与△CPE相似.
6如图,四边形ABCD为平行四边形,E为边 AD 上一点,连接 AC,BE,它们相交于点 F,且∠ACB=∠ABE.
(1)求证:
(2)若AE=2,EF=1,CF=4,求AB的长.
7(1)如图①,在 Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为 D,求AD的长.
(2)如图②,△ABC中,AC=14,BC=6,点 D,E分别在线段AB,AC 上,∠EDB=∠ACB=60°,DE=2,求AD 的长.
创新拓展题
8.【问题探究】
课外兴趣小组活动时,同学们在解决如下问题:如图①,在矩形 ABCD中,点 E,F 分别是边DC,BC上的点,连接AE,DF,且AE⊥DF 于点G,若AB=6,BC=8,求 的值.
(1)请你帮助同学们解决上述问题.
【初步运用】
(2)如图②,在△ABC中, 点 D 为AC的中点,连接 BD,过点 A 作 AE⊥BD于点E,交BC于点 F,求 的值.
【灵活运用】
(3)如图③,在四边形 ABCD 中,∠BAD=90°, 点 E,F 分别在边AB,AD 上,且 DE⊥CF,垂足为 G,则
*5相似三角形判定定理的证明
1. B
2 【点拨】如图,连接CE
∵∠CAD=30°,∠ACD=90°,E是AD的中点,
易得
∴∠ACE=∠CAE=30°.
∵∠BAC=30°,∠ABC=90°,
∴∠BAC=∠ACE,易得
∴AB∥CE.∴∠ABF=∠CEF.∴△ABF∽△CEF.
3.【证明】(1)∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ADE=60°,∴∠ADE=∠ACB.
又∵∠DAC=∠EAD,
∴△ACD∽△ADE.
(2)由(1)得△ACD∽△ADE,∴∠ADC=∠E.
∵△ABC是等边三角形,∴∠ACD=∠ABC=60°.
∴∠ABD=∠ECD=120°.
又∵∠ADB=∠E,
∴△ABD∽△DCE.
4. C 【点拨】∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC.∴∠FED=∠FBC,∠FDE=∠FCB.
∴△DEF∽△CBF.
··器=ぴ.∵DC=2DF,∴CF=3DF.
‥器 .‥器 .∵AD∥BC,∴∠GAE=∠GCB∠GEA=∠GBC.
故选 C.
5.12 或 16 或 21 【点拨】易得∠B=∠C.若△BDP∽△CPE,则 或4 cm. 或
若△BDP∽△CEP,则
综上所述,当t=12 或 16 或 21 时,△BDP 与△CPE相似.
6.(1)【证明】∵四边形ABCD为平行四边形,
∴AD∥BC.
∴∠DAC=∠ACB.
又∵∠ACB=∠ABE,
∴∠DAC=∠ABE.
又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
∴EA: EB=EF: EA.
(2)【解】
∴BF=BE-EF=4-1=3.
∵AE∥BC,
即 解得
∵△EAF∽△EBA,
即
7.【解】(1)∵ED⊥AB,∴∠ADE=90°=∠C.
又∵∠A=∠A,
∵AB=10,AC=8,AE=5,
解得AD=4.
(2)在AC上截取CH=CB,连接BH.
∵∠ACB=60°,
∴△BCH为等边三角形.
∴CH=BH=BC=6,∠CHB=60°.
∴AH=AC-CH=8,∠AHB=120°.
∵∠EDB=60°,
∴∠ADE=120°.∴∠ADE=∠AHB.
又∵∠A=∠A,
∴△ADE∽△AHB.∴BB=AB,即 解得
8.【解】(1)∵AE⊥DF,∴∠EGD=90°.
∴∠EDG+∠DEG=90°.
∵四边形ABCD为矩形,
∴AB=CD=6,BC=AD=8,∠C=∠ADE=90°.
∴∠EDG+∠DFC=90°.∴∠DEG=∠DFC.
(2)构造如图①所示矩形ABHC,延长AF交CH 于点G,由(1)中结论可得△ABD∽△CAG.
∴设AB=3k,AC=4k.
∵点 D为AC 的中点,
在 Rt△ABD中,根据勾股定理可得
∵△ABD∽△CAG,
则 解得
∵四边形ABHC为矩形,∴AB∥CG.
∴∠BAF=∠CGF,∠ABF=∠GCF.
∴△ABF∽△GCF.
即
解得
(3 【点拨】连接 BD,构造如图②所示的矩形AMND过点 N作NP∥CF,交AD于点P,连接 BD.
∵AB=BC,AD=CD,BD=BD,
∴△ABD≌△CBD.
∴∠BCD=∠A=90°.
∴∠BCM+∠DCN=90°.
∵四边形 AMND 为矩形,
∴MN=AD,DN=AM,AD∥MN,∠M=∠MND=90°.
∴∠BCM+∠CBM=90°,∴∠DCN=∠CBM.
又∵∠M=∠CND=90°,∴△DCN∽△CBM.
∴设AB=BC=3k,AD=CD=4k.
设 BM=3x,CN=4x,
则CM=MN-CN=AD-CN=4k-4x,DN=AM=AB+BM=3k+3x,
整理得
由(1)中结论可得
∵NP∥CF,CN∥PF,
∴四边形 FCNP 为平行四边形,
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
