4.2 平行线分线段成比例同步练习(含答案) 2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 4.2 平行线分线段成比例同步练习(含答案) 2024-2025学年北师大版九年级数学上册 | 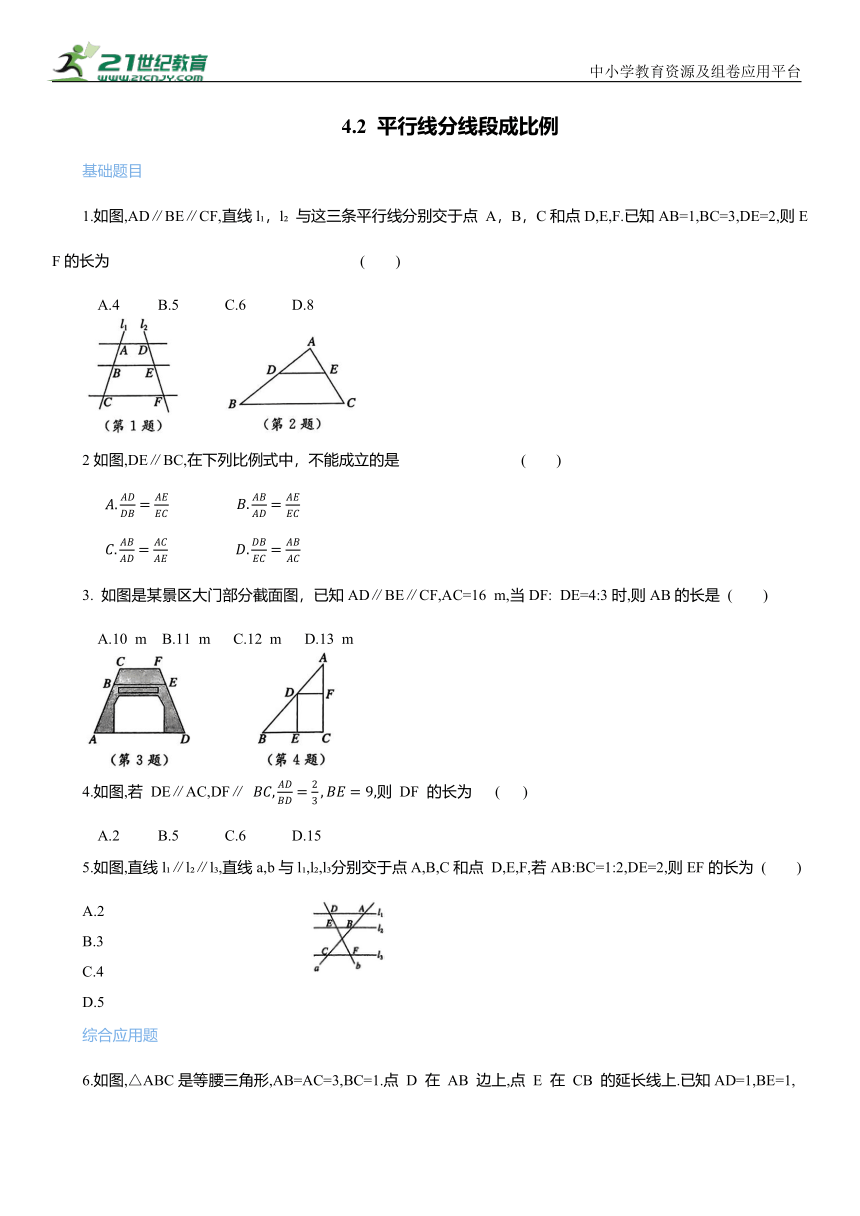 | |
| 格式 | docx | ||
| 文件大小 | 416.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 10:04:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
4.2 平行线分线段成比例
基础题目
1.如图,AD∥BE∥CF,直线l ,l 与这三条平行线分别交于点 A,B,C和点D,E,F.已知AB=1,BC=3,DE=2,则EF的长为 ( )
A.4 B.5 C.6 D.8
2如图,DE∥BC,在下列比例式中,不能成立的是 ( )
3. 如图是某景区大门部分截面图,已知AD∥BE∥CF,AC=16 m,当DF: DE=4:3时,则AB的长是 ( )
A.10 m B.11 m C.12 m D.13 m
4.如图,若 DE∥AC,DF∥ 则 DF 的长为 ( )
A.2 B.5 C.6 D.15
5.如图,直线l ∥l ∥l ,直线a,b与l ,l ,l 分别交于点A,B,C和点 D,E,F,若AB:BC=1:2,DE=2,则EF的长为 ( )
A.2
B.3
C.4
D.5
综合应用题
6.如图,△ABC是等腰三角形,AB=AC=3,BC=1.点 D 在 AB 边上,点 E 在 CB 的延长线上.已知AD=1,BE=1,连接ED并延长交AC于点 F,则线段AF 的长为 ( )
A B C D.1
7.如图,在△ABC中,D 是BC边上的中点,AF: FD=1:2,BF的延长线交 AC于点 E,则AE: CE 的值为 ( )
A B C D
8如图是一架梯子的示意图,其中 ,且 AB=BC=CD,为使其更稳固,在A,D 间加绑一条安全绳(线段 AD ),量得 AE=0.4 m,则
9.在△ABC中,AB=6,AC=9,点 D在边 AB所在的直线上,且 AD=2,过点 D 作 DE∥BC交边AC 所在直线于点 E,则 CE 的长为 .
10.如图,已知AC∥FE∥BD,求证:
11. 如图,在矩形ABCD中,AB=5,BC=4,动点 P 从点 B出发,以每秒2个单位长度的速度,沿射线 BC方向运动,动点 Q从点 C出发,以每秒1个单位长度的速度,沿线段CD方向运动.点P和点Q同时出发,当点 Q到达点D 时,两点同时停止运动,设运动时间为 t秒(t>0).
(1)用含 t的代数式表示线段CP 的长;
(2)当PQ与矩形的对角线平行时,求t的值,
创新拓展题
12.一般地,有如下基本事实:
两条直线被一组平行线所截,所得的对应
线段成比例.
【问题原型】如图①,在矩形 ABCD 中,点 E为边 AB 的中点,过点 E 作 EF ∥AD 交边DC 于点F,点 P,Q分别在矩形的边AD,BC上,连接PQ交EF于点M.求证:PM=QM.【结论应用】在【问题原型】的基础上,点R 在边BC 上(不与点Q重合),连接PR 交EF 于点 N.
(1)如图②,若MN=4,则线段QR 的长为 ;
(2)当点 Q 与点B 重合,点R 与点 C 重合时,如图③,若BC=10,且△PMN周长的最小值为12,则边AB的长为 .
2 平行线分线段成比例
1. C 2. B 3. C 4. C 5. C
6. B 【点拨】取 CF的中点G,连接 BG.
∵BC=1,BE=1,
∴点 B为EC 的中点.
∴BG是△CEF的中位线.
∴BG∥EF.
∴CG=FG=2AF.
∴AC=AF+FG+CG=5AF=3.
7. C 【点拨】如图,过点 D作 DM∥BE,交 AC于点 M.
∵D 是 BC 边上的中点,
∴BD=CD.
∵DM∥BE,
∴CE=EM+CM=2EM.
8.1.2 【点拨】
又∵AE=0.4m ,
9.6或12 【点拨】如图①,当点 D 在边AB 上时,∵AB=6,AC=9,AD=2,∴BD=4.∵DE∥BC,.. BB=≌C,即 解得CE=6;如图②,当点 D 在边 BA 的延长线上时,∵AB=6,AC=9,AD=2,
∴BD=8.∵DE∥BC,
即 解得 CE=12.
综上所述,CE的长为6或12.
10.【证明】∵AC∥EF,
∵FE∥BD,
①+②,得 即
11.【解】(1)∵四边形ABCD为矩形,AB=5,BC=4,∴CD=AB=5,AD=BC=4,AD∥BC.
∵点Q在CD上运动,运动的速度为每秒1个单位长度,
且点 Q到达点D 时停止运动,
∴点Q从点C运动到点D 所用的时间为5÷1=5(秒),且 CQ=t.
∴0∵动点P从点B出发,以每秒2个单位长度的速度,运动时间为l秒(t>0),
∴BP=2t.
①当0②当2(2)当PQ与矩形ABCD 的对角平行时,有以下两种情况:①当 PQ∥BD时,此时点 P 在线段BC 上,如图①,
则0根据平行线分线段成比例定理,得CP:CB=CQ:CD,即(4-2t):4=t:5,解得
②当PQ∥AC时,此时点 P在BC 的延长线上,设 PQ的延长线交AD 于点M,如图②,
则2∵AD∥BC,PQ∥AC,
∴四边形 ACPM为平行四边形.
∴AM=CP=2t-4.
根据平行线分线段成比例定理,得AM:AD=CQ:CD.即(2t-4):4=t:5,解得
综上所述,当PQ与矩形的对角线平行时,t的值 或
12.【问题原型】【证明】∵点E为边AB 的中点,
∴AE=BE.
∵四边形ABCD是矩形,∴AD∥BC.
∵EF∥AD,∴AD∥EF∥BC.
∴PM=QM.
【结论应用】(1)8
(2) 【点拨】如图所示
作点 C 关于 AD 的对称点 G,连接PG,BG,∴PG=PC.
∴PB+PC=PB+PG≥BG.
∴当点 P 在BG 上时,PB+PC取得最小值.
又∵PD∥BC,D是CG的中点,∴点 P是BG 的中点.
∴PB=PG=PC,易证P是AD的中点.
即当 P是AD的中点时,△PBC的周长取得最小值.
根据(1)的结论得出 MN 是△PQR 的中位线.
又∵BC=10,且△PMN周长的最小值为12,
易得△PBC 的周长为 24.
∴PB+PC=24-10=14.
∴PB=7.
4.2 平行线分线段成比例
基础题目
1.如图,AD∥BE∥CF,直线l ,l 与这三条平行线分别交于点 A,B,C和点D,E,F.已知AB=1,BC=3,DE=2,则EF的长为 ( )
A.4 B.5 C.6 D.8
2如图,DE∥BC,在下列比例式中,不能成立的是 ( )
3. 如图是某景区大门部分截面图,已知AD∥BE∥CF,AC=16 m,当DF: DE=4:3时,则AB的长是 ( )
A.10 m B.11 m C.12 m D.13 m
4.如图,若 DE∥AC,DF∥ 则 DF 的长为 ( )
A.2 B.5 C.6 D.15
5.如图,直线l ∥l ∥l ,直线a,b与l ,l ,l 分别交于点A,B,C和点 D,E,F,若AB:BC=1:2,DE=2,则EF的长为 ( )
A.2
B.3
C.4
D.5
综合应用题
6.如图,△ABC是等腰三角形,AB=AC=3,BC=1.点 D 在 AB 边上,点 E 在 CB 的延长线上.已知AD=1,BE=1,连接ED并延长交AC于点 F,则线段AF 的长为 ( )
A B C D.1
7.如图,在△ABC中,D 是BC边上的中点,AF: FD=1:2,BF的延长线交 AC于点 E,则AE: CE 的值为 ( )
A B C D
8如图是一架梯子的示意图,其中 ,且 AB=BC=CD,为使其更稳固,在A,D 间加绑一条安全绳(线段 AD ),量得 AE=0.4 m,则
9.在△ABC中,AB=6,AC=9,点 D在边 AB所在的直线上,且 AD=2,过点 D 作 DE∥BC交边AC 所在直线于点 E,则 CE 的长为 .
10.如图,已知AC∥FE∥BD,求证:
11. 如图,在矩形ABCD中,AB=5,BC=4,动点 P 从点 B出发,以每秒2个单位长度的速度,沿射线 BC方向运动,动点 Q从点 C出发,以每秒1个单位长度的速度,沿线段CD方向运动.点P和点Q同时出发,当点 Q到达点D 时,两点同时停止运动,设运动时间为 t秒(t>0).
(1)用含 t的代数式表示线段CP 的长;
(2)当PQ与矩形的对角线平行时,求t的值,
创新拓展题
12.一般地,有如下基本事实:
两条直线被一组平行线所截,所得的对应
线段成比例.
【问题原型】如图①,在矩形 ABCD 中,点 E为边 AB 的中点,过点 E 作 EF ∥AD 交边DC 于点F,点 P,Q分别在矩形的边AD,BC上,连接PQ交EF于点M.求证:PM=QM.【结论应用】在【问题原型】的基础上,点R 在边BC 上(不与点Q重合),连接PR 交EF 于点 N.
(1)如图②,若MN=4,则线段QR 的长为 ;
(2)当点 Q 与点B 重合,点R 与点 C 重合时,如图③,若BC=10,且△PMN周长的最小值为12,则边AB的长为 .
2 平行线分线段成比例
1. C 2. B 3. C 4. C 5. C
6. B 【点拨】取 CF的中点G,连接 BG.
∵BC=1,BE=1,
∴点 B为EC 的中点.
∴BG是△CEF的中位线.
∴BG∥EF.
∴CG=FG=2AF.
∴AC=AF+FG+CG=5AF=3.
7. C 【点拨】如图,过点 D作 DM∥BE,交 AC于点 M.
∵D 是 BC 边上的中点,
∴BD=CD.
∵DM∥BE,
∴CE=EM+CM=2EM.
8.1.2 【点拨】
又∵AE=0.4m ,
9.6或12 【点拨】如图①,当点 D 在边AB 上时,∵AB=6,AC=9,AD=2,∴BD=4.∵DE∥BC,.. BB=≌C,即 解得CE=6;如图②,当点 D 在边 BA 的延长线上时,∵AB=6,AC=9,AD=2,
∴BD=8.∵DE∥BC,
即 解得 CE=12.
综上所述,CE的长为6或12.
10.【证明】∵AC∥EF,
∵FE∥BD,
①+②,得 即
11.【解】(1)∵四边形ABCD为矩形,AB=5,BC=4,∴CD=AB=5,AD=BC=4,AD∥BC.
∵点Q在CD上运动,运动的速度为每秒1个单位长度,
且点 Q到达点D 时停止运动,
∴点Q从点C运动到点D 所用的时间为5÷1=5(秒),且 CQ=t.
∴0
∴BP=2t.
①当0
则0
②当PQ∥AC时,此时点 P在BC 的延长线上,设 PQ的延长线交AD 于点M,如图②,
则2
∴四边形 ACPM为平行四边形.
∴AM=CP=2t-4.
根据平行线分线段成比例定理,得AM:AD=CQ:CD.即(2t-4):4=t:5,解得
综上所述,当PQ与矩形的对角线平行时,t的值 或
12.【问题原型】【证明】∵点E为边AB 的中点,
∴AE=BE.
∵四边形ABCD是矩形,∴AD∥BC.
∵EF∥AD,∴AD∥EF∥BC.
∴PM=QM.
【结论应用】(1)8
(2) 【点拨】如图所示
作点 C 关于 AD 的对称点 G,连接PG,BG,∴PG=PC.
∴PB+PC=PB+PG≥BG.
∴当点 P 在BG 上时,PB+PC取得最小值.
又∵PD∥BC,D是CG的中点,∴点 P是BG 的中点.
∴PB=PG=PC,易证P是AD的中点.
即当 P是AD的中点时,△PBC的周长取得最小值.
根据(1)的结论得出 MN 是△PQR 的中位线.
又∵BC=10,且△PMN周长的最小值为12,
易得△PBC 的周长为 24.
∴PB+PC=24-10=14.
∴PB=7.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
