第四章图形的相似全章热门考点整合应用(含答案) 2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 第四章图形的相似全章热门考点整合应用(含答案) 2024-2025学年北师大版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 635.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 10:09:32 | ||
图片预览



文档简介
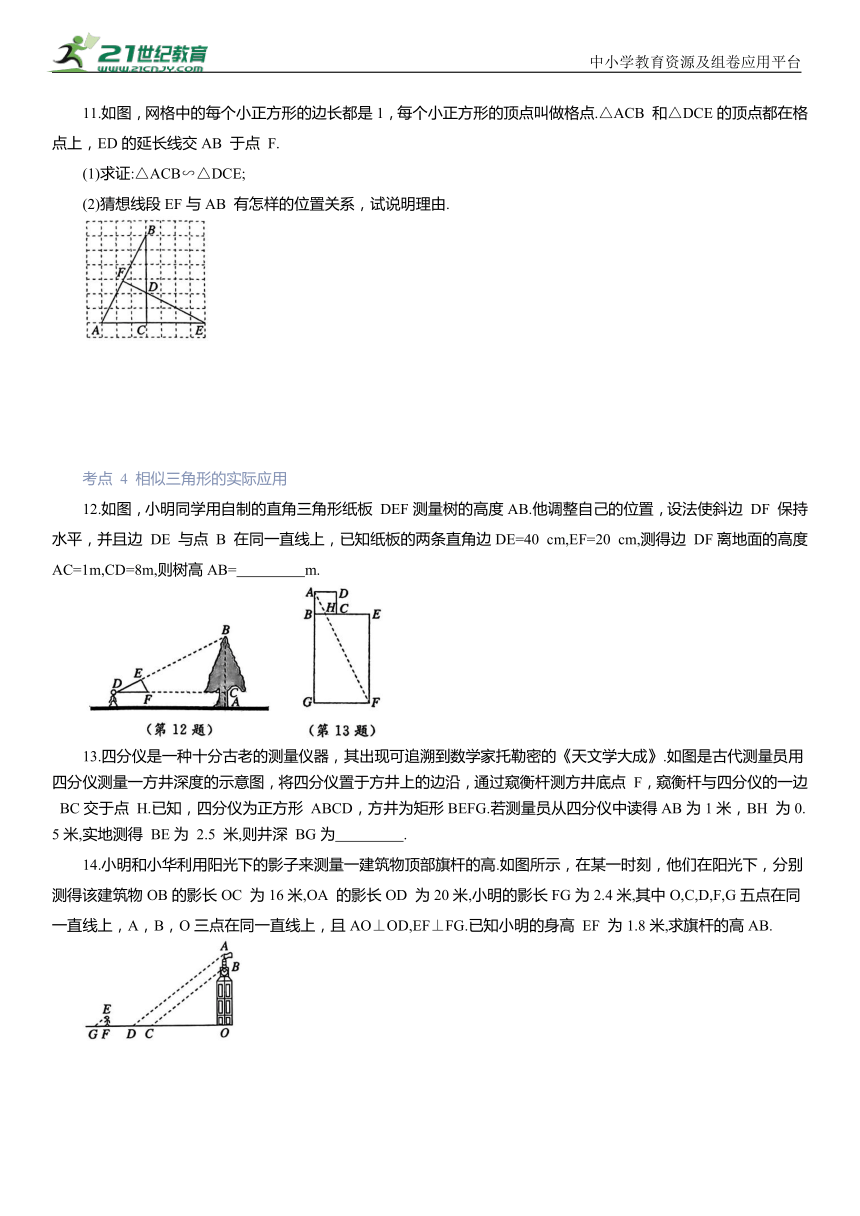
第四章图形的相似全章热门考点整合应用
核心考点整合
考点1 成比例线段及平行线分线段成比例
1.如图,l ∥l ∥l ,若 则 DE等于 ( )
A.4 B.6 C.8 D.9
2.如图,l ∥l ∥l ,两条直线与这三条平行线分别交于点A,B,C和点 D,E,F,若 则 的值为 ( )
A B C D
3.已知线段x,y,z,且
(1)求 的值;
(2)如果线段 x,y,z满足 3x--4y+5z=54,求x--2y+z的值.
考点 2 相似多边形及黄金分割
4.如图,有甲,乙,丙三个矩形,其中相似的是 ( )
A.甲与丙 B.甲与乙
C.乙与丙 D.三个矩形都不相似
5.,红透的枫叶总能牵动人们无尽的思绪,所以诗人杜牧说:“停车坐爱枫林晚,霜叶红于二月花”.如图是两片形状相同的枫叶图案,则x的值为 .
6.新视角 新定义题 定义:如图①,点C 在线段 AB上,若满足AC =BC·AB,则称点C为线段AB的黄金分割点.
运用:如图②,△ABC中,AB=AC,∠B=72°,∠ACB的平分线CD交AB 于点 D.
(1)求证:点D是线段AB 的黄金分割点;
(2)若AC=2,求 BC的长.
考点 3 相似三角形的判定和性质
7.如图,P为Rt△ABC斜边AB 上任意一点(除A,B外),过点 P 作直线截△ABC,使截得的新三角形与△ABC相似,满足这样条件的直线的作法共有 ( )
A.1种
B.2种
C.3种
D.4 种
8.已知△ABC∽△A'B'C',AD,A'D'分别是△ABC和△A'B'C'的角平分线,且 AD:. 下面给出的四个结论中,正确的结论有 ( )
①③
A.1个 B.2个 C.3个 D.4个
9.如图,将△ABC 绕点 A按逆时针方向旋转得到△ADE,点C的对应点E恰好落在边 BC的延长线上,AD 与 BE 相交 于 点 F,若 则
10.如图,在矩形 ABCD中,M为BC上一点,EM⊥AM交AD的延长线于点 E.
(1)求证:△ABM∽△EMA;
(2)若AB=4,BM=3,求AE的值.
11.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB 和△DCE的顶点都在格点上,ED的延长线交AB 于点 F.
(1)求证:△ACB∽△DCE;
(2)猜想线段EF与AB 有怎样的位置关系,试说明理由.
考点 4 相似三角形的实际应用
12.如图,小明同学用自制的直角三角形纸板 DEF测量树的高度AB.他调整自己的位置,设法使斜边 DF 保持水平,并且边 DE 与点 B 在同一直线上,已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边 DF离地面的高度AC=1m,CD=8m,则树高AB= m.
13.四分仪是一种十分古老的测量仪器,其出现可追溯到数学家托勒密的《天文学大成》.如图是古代测量员用四分仪测量一方井深度的示意图,将四分仪置于方井上的边沿,通过窥衡杆测方井底点 F,窥衡杆与四分仪的一边 BC交于点 H.已知,四分仪为正方形 ABCD,方井为矩形BEFG.若测量员从四分仪中读得AB为1米,BH 为0.5米,实地测得 BE为 2.5 米,则井深 BG为 .
14.小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC 为16米,OA 的影长OD 为20米,小明的影长FG为2.4米,其中O,C,D,F,G五点在同一直线上,A,B,O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高 EF 为1.8米,求旗杆的高AB.
考点 5 位似
15.在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点△ABC,△DEF成位似关系,则位似中心的坐标为 ( )
A.(--1,0) B.(0,0)
C.(0,1) D.(1,0)
16.如图,△ABO的顶点坐标是A(2,6),B(3,1),O(0,0),以点O为位似中心,将△ABO缩小为原来 ,得到△A'B'O,则点A'的标为 .
17.如图,A,B,O三点都在方格纸的格点上,请按要求在方格纸内作图.
(1)在图①中以点O为位似中心,作线段 AB 的位似图形CD,使其长度为AB的2倍.
(2)已知△OPQ的三边比为1:2 ,在图②画格点△ABD,使△ABD与△OPQ相似.
中小学教育资源及组卷应用平台
1. B 2. A
3. 【解
∴设x=3k,y=4k,z=5k.
(2)∵3x-4y+5z=54,
∴9k-16k+25k=54.
∴k=3.∴x=9,y=12,z=15.
∴x-2y+z=9-24+15=0.
4. A 5.11
6.(1)【证明】∵∠B=72°,AB=AC,
∴∠ACB=∠B=72°.
∴∠A=36°.
∵CD平分∠ACB,
∴∠A=∠ACD,∠CDB=72°.
∴AD=CD,∠CDB=∠B.
∴BC=CD.∴BC=AD.
∵∠B=∠B,∠BCD=∠A=36°,
∴△BAC∽△BCD.
∴BC: AB=BD: BC.
∴AD:AB=BD:AD.
∴点 D 是线段 AB 的黄金分割点.
(2)【解】∵点D是线段AB 的黄金分割点,
由(1)知BC=AD,
7. C 【点拨】如图,过点 P可作PE∥BC或PE ∥AC,所得三角形与△ABC相似.过点 P 还可作 PE'⊥AB,可得 90°,∠A=∠A,
∴△APE'∽△ACB.
∴共有 3 种.故选 C.
8. B 【点拨】∵△ABC∽△A'B'C',AD 和A'D'分别是△ABC,△A'B'C'的角平分线,且AD: ∴正确的结论有2个.
故选 B.
9 【点拨】由旋转得
设点A 到BE的距离为h,则
10.(1)【证明】∵四边形ABCD为矩形,
∴∠B=9Q°,AD∥BC.
∴∠EAM=∠AMB.
∵EM⊥AM,
∴∠AME=90°.
∴∠B=∠AME.
∴△ABM∽△EMA.
(2)【解】∵AB=4,BM=3,∠B=90°,
∵△ABM∽△EMA,
11.(1)【证明】∵AC=3,CD=2,BC=6,CE=4,
又∵∠ACB=∠DCE=90°,
∴△ACB∽△DCE.
(2)【解】猜想线段 EF⊥AB.理由如下:
∵△ACB∽△DCE,∴∠B=∠E.
∵∠ACB=90°,∴∠A+∠B=90°.∴∠A+∠E=90°.
∴∠AFE=90°,即 EF⊥AB.
12.5 【点拨】∵∠DEF=∠BCD=90°,∠D=∠D,
∵DE=40 cm=0. 4m ,EF=20cm=0.2m,CD=8m,
∴AB=AC+BC=1+4=5(m).
13.4米 【点拨】∵四边形ABCD是正方形,
∴∠ABC=90°.
∵BE=2.5米,BH=0.5米,
∴HE=BE-BH=2.5-0.5=2(米).
∵四边形 BEFG是矩形,
∴BG=EF,∠BEF=90°.
∴∠ABH=∠FEH=90°.
又∵∠AHB=∠FHE,
∴△ABH∽△FEH.
∴EF=4米.∴BG=4米.
14.【解】∵AD∥EG,
∴∠ADO=∠EGF.
∵AO⊥OD,EF⊥FG,∴∠AOD=∠EFG≈90°,
∴△AOD∽△EFG
即
∴AO=15米.
∵AD∥BC,
∴∠BCO=∠ADO,∠DAO=∠CBO.
∴△BOC∽△AOD.
即
∴BO=12米.
∴AB=AO-BO=15-12=3(米).
∴旗杆的高AB 是 3 米.
15. A
16. ,2)或 【点拨】∵以原点O为位似中心,把△ABO缩小为原来 ,可以得到△A'B'O,点 的坐标为(2,6),∴点A'的坐标是 或 ,即 ,2)或
17.【解】(1)如图①,线段CD即为所求.(答案不唯一)
(2)如图②,△ABD 即为所求(答案不唯一).
核心考点整合
考点1 成比例线段及平行线分线段成比例
1.如图,l ∥l ∥l ,若 则 DE等于 ( )
A.4 B.6 C.8 D.9
2.如图,l ∥l ∥l ,两条直线与这三条平行线分别交于点A,B,C和点 D,E,F,若 则 的值为 ( )
A B C D
3.已知线段x,y,z,且
(1)求 的值;
(2)如果线段 x,y,z满足 3x--4y+5z=54,求x--2y+z的值.
考点 2 相似多边形及黄金分割
4.如图,有甲,乙,丙三个矩形,其中相似的是 ( )
A.甲与丙 B.甲与乙
C.乙与丙 D.三个矩形都不相似
5.,红透的枫叶总能牵动人们无尽的思绪,所以诗人杜牧说:“停车坐爱枫林晚,霜叶红于二月花”.如图是两片形状相同的枫叶图案,则x的值为 .
6.新视角 新定义题 定义:如图①,点C 在线段 AB上,若满足AC =BC·AB,则称点C为线段AB的黄金分割点.
运用:如图②,△ABC中,AB=AC,∠B=72°,∠ACB的平分线CD交AB 于点 D.
(1)求证:点D是线段AB 的黄金分割点;
(2)若AC=2,求 BC的长.
考点 3 相似三角形的判定和性质
7.如图,P为Rt△ABC斜边AB 上任意一点(除A,B外),过点 P 作直线截△ABC,使截得的新三角形与△ABC相似,满足这样条件的直线的作法共有 ( )
A.1种
B.2种
C.3种
D.4 种
8.已知△ABC∽△A'B'C',AD,A'D'分别是△ABC和△A'B'C'的角平分线,且 AD:. 下面给出的四个结论中,正确的结论有 ( )
①③
A.1个 B.2个 C.3个 D.4个
9.如图,将△ABC 绕点 A按逆时针方向旋转得到△ADE,点C的对应点E恰好落在边 BC的延长线上,AD 与 BE 相交 于 点 F,若 则
10.如图,在矩形 ABCD中,M为BC上一点,EM⊥AM交AD的延长线于点 E.
(1)求证:△ABM∽△EMA;
(2)若AB=4,BM=3,求AE的值.
11.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB 和△DCE的顶点都在格点上,ED的延长线交AB 于点 F.
(1)求证:△ACB∽△DCE;
(2)猜想线段EF与AB 有怎样的位置关系,试说明理由.
考点 4 相似三角形的实际应用
12.如图,小明同学用自制的直角三角形纸板 DEF测量树的高度AB.他调整自己的位置,设法使斜边 DF 保持水平,并且边 DE 与点 B 在同一直线上,已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边 DF离地面的高度AC=1m,CD=8m,则树高AB= m.
13.四分仪是一种十分古老的测量仪器,其出现可追溯到数学家托勒密的《天文学大成》.如图是古代测量员用四分仪测量一方井深度的示意图,将四分仪置于方井上的边沿,通过窥衡杆测方井底点 F,窥衡杆与四分仪的一边 BC交于点 H.已知,四分仪为正方形 ABCD,方井为矩形BEFG.若测量员从四分仪中读得AB为1米,BH 为0.5米,实地测得 BE为 2.5 米,则井深 BG为 .
14.小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC 为16米,OA 的影长OD 为20米,小明的影长FG为2.4米,其中O,C,D,F,G五点在同一直线上,A,B,O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高 EF 为1.8米,求旗杆的高AB.
考点 5 位似
15.在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点△ABC,△DEF成位似关系,则位似中心的坐标为 ( )
A.(--1,0) B.(0,0)
C.(0,1) D.(1,0)
16.如图,△ABO的顶点坐标是A(2,6),B(3,1),O(0,0),以点O为位似中心,将△ABO缩小为原来 ,得到△A'B'O,则点A'的标为 .
17.如图,A,B,O三点都在方格纸的格点上,请按要求在方格纸内作图.
(1)在图①中以点O为位似中心,作线段 AB 的位似图形CD,使其长度为AB的2倍.
(2)已知△OPQ的三边比为1:2 ,在图②画格点△ABD,使△ABD与△OPQ相似.
中小学教育资源及组卷应用平台
1. B 2. A
3. 【解
∴设x=3k,y=4k,z=5k.
(2)∵3x-4y+5z=54,
∴9k-16k+25k=54.
∴k=3.∴x=9,y=12,z=15.
∴x-2y+z=9-24+15=0.
4. A 5.11
6.(1)【证明】∵∠B=72°,AB=AC,
∴∠ACB=∠B=72°.
∴∠A=36°.
∵CD平分∠ACB,
∴∠A=∠ACD,∠CDB=72°.
∴AD=CD,∠CDB=∠B.
∴BC=CD.∴BC=AD.
∵∠B=∠B,∠BCD=∠A=36°,
∴△BAC∽△BCD.
∴BC: AB=BD: BC.
∴AD:AB=BD:AD.
∴点 D 是线段 AB 的黄金分割点.
(2)【解】∵点D是线段AB 的黄金分割点,
由(1)知BC=AD,
7. C 【点拨】如图,过点 P可作PE∥BC或PE ∥AC,所得三角形与△ABC相似.过点 P 还可作 PE'⊥AB,可得 90°,∠A=∠A,
∴△APE'∽△ACB.
∴共有 3 种.故选 C.
8. B 【点拨】∵△ABC∽△A'B'C',AD 和A'D'分别是△ABC,△A'B'C'的角平分线,且AD: ∴正确的结论有2个.
故选 B.
9 【点拨】由旋转得
设点A 到BE的距离为h,则
10.(1)【证明】∵四边形ABCD为矩形,
∴∠B=9Q°,AD∥BC.
∴∠EAM=∠AMB.
∵EM⊥AM,
∴∠AME=90°.
∴∠B=∠AME.
∴△ABM∽△EMA.
(2)【解】∵AB=4,BM=3,∠B=90°,
∵△ABM∽△EMA,
11.(1)【证明】∵AC=3,CD=2,BC=6,CE=4,
又∵∠ACB=∠DCE=90°,
∴△ACB∽△DCE.
(2)【解】猜想线段 EF⊥AB.理由如下:
∵△ACB∽△DCE,∴∠B=∠E.
∵∠ACB=90°,∴∠A+∠B=90°.∴∠A+∠E=90°.
∴∠AFE=90°,即 EF⊥AB.
12.5 【点拨】∵∠DEF=∠BCD=90°,∠D=∠D,
∵DE=40 cm=0. 4m ,EF=20cm=0.2m,CD=8m,
∴AB=AC+BC=1+4=5(m).
13.4米 【点拨】∵四边形ABCD是正方形,
∴∠ABC=90°.
∵BE=2.5米,BH=0.5米,
∴HE=BE-BH=2.5-0.5=2(米).
∵四边形 BEFG是矩形,
∴BG=EF,∠BEF=90°.
∴∠ABH=∠FEH=90°.
又∵∠AHB=∠FHE,
∴△ABH∽△FEH.
∴EF=4米.∴BG=4米.
14.【解】∵AD∥EG,
∴∠ADO=∠EGF.
∵AO⊥OD,EF⊥FG,∴∠AOD=∠EFG≈90°,
∴△AOD∽△EFG
即
∴AO=15米.
∵AD∥BC,
∴∠BCO=∠ADO,∠DAO=∠CBO.
∴△BOC∽△AOD.
即
∴BO=12米.
∴AB=AO-BO=15-12=3(米).
∴旗杆的高AB 是 3 米.
15. A
16. ,2)或 【点拨】∵以原点O为位似中心,把△ABO缩小为原来 ,可以得到△A'B'O,点 的坐标为(2,6),∴点A'的坐标是 或 ,即 ,2)或
17.【解】(1)如图①,线段CD即为所求.(答案不唯一)
(2)如图②,△ABD 即为所求(答案不唯一).
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
