相似三角形的性质及应用 同步练习(含答案) 2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 相似三角形的性质及应用 同步练习(含答案) 2024-2025学年北师大版九年级数学上册 | 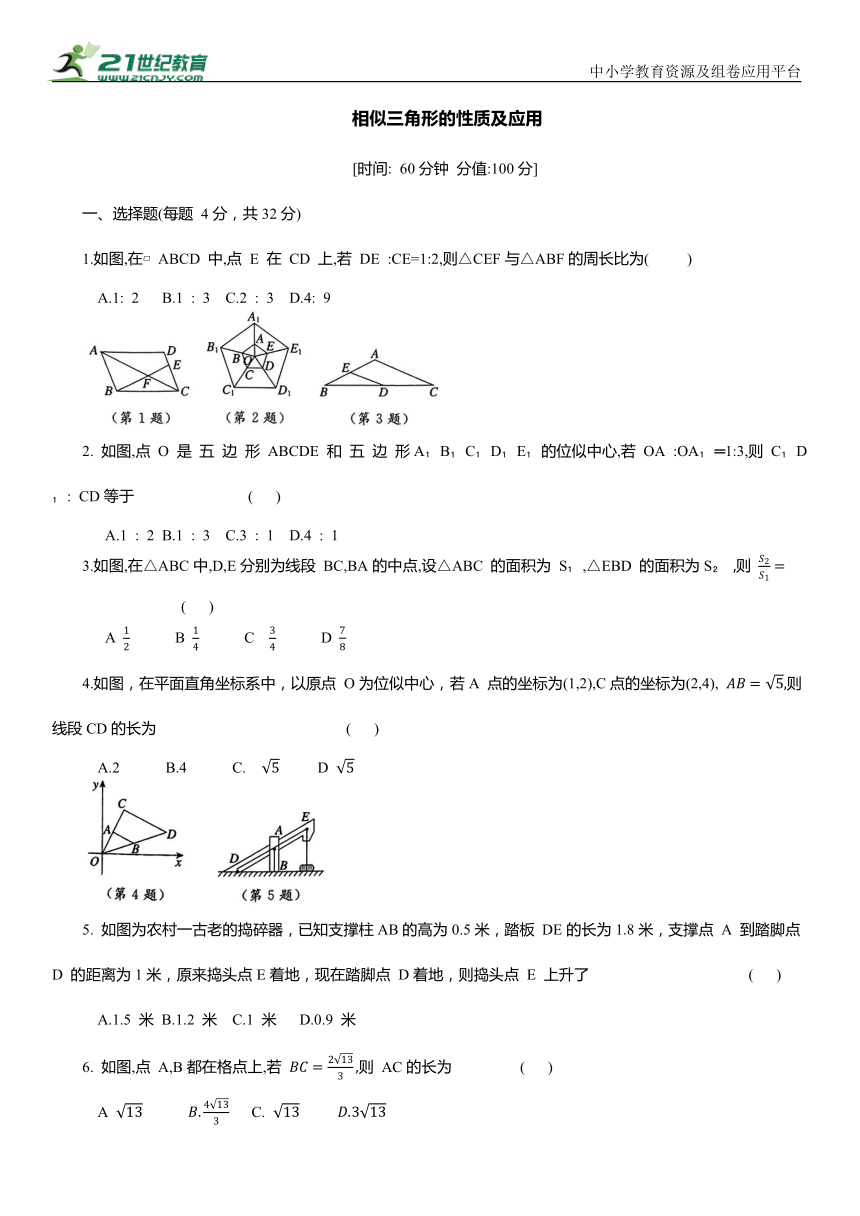 | |
| 格式 | docx | ||
| 文件大小 | 652.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 10:14:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
相似三角形的性质及应用
[时间: 60分钟 分值:100分]
一、选择题(每题 4分,共32分)
1.如图,在 ABCD 中,点 E 在 CD 上,若 DE :CE=1:2,则△CEF与△ABF的周长比为( )
A.1: 2 B.1 : 3 C.2 : 3 D.4: 9
2. 如图,点 O 是 五 边 形 ABCDE 和 五 边 形A B C D E 的位似中心,若 OA :OA ═1:3,则 C D : CD等于 ( )
A.1 : 2 B.1 : 3 C.3 : 1 D.4 : 1
3.如图,在△ABC中,D,E分别为线段 BC,BA的中点,设△ABC 的面积为 S ,△EBD 的面积为S ,则 ( )
A B C D
4.如图,在平面直角坐标系中,以原点 O为位似中心,若A 点的坐标为(1,2),C点的坐标为(2,4), 则线段CD的长为 ( )
A.2 B.4 C. D
5. 如图为农村一古老的捣碎器,已知支撑柱AB的高为0.5米,踏板 DE的长为1.8米,支撑点 A 到踏脚点 D 的距离为1米,原来捣头点E着地,现在踏脚点 D着地,则捣头点 E 上升了 ( )
A.1.5 米 B.1.2 米 C.1 米 D.0.9 米
6. 如图,点 A,B都在格点上,若 则 AC的长为 ( )
A C.
7.由12个有公共顶点 O的直角三角形拼成如图所示的图形.∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB =1,则图中与△AOB位似的三角形的面积为 ( )
D.
8.如图是一个由A,B,C三种相似的直角三角形纸片(C与B,B与A的相似比相同)拼成的矩形,相邻纸片之间互不重叠也无缝隙,其中A,B,C的纸片的面积分别 S ,S ,S ,若 S > ,则这个矩形的面积一定可以表示为
( )
A.4S B.6S
二、填空题(每题5分,共20分)
9.如图,在平面直角坐标系中,△ABC与△A B C 位似,原点 O是位似中心,且 3.若A(9,3),则 A 的坐标是 .
10.如果两个相似三角形的最长边分别是 35 cm和14 cm,它们的周长之差为 60 cm,那么这两个三角形的周长分别是 .
11.如图,在△ABC中,AC=BC=16,点 D在AB上,点 E 在BC上,点B关于直线DE 的轴对称点为点 B',连接DB',EB',分别与AC相交于F 点,G点,若AF=8,DF=7,B'F=4,,则CG的长度为 .
12.如图,在 Rt△ABC中,∠C=90°,AC=3,BC=1,将△ABC 绕点 A 逆时针方向旋转90°,得到△AB'C'.连接 BB',交AC于点 D,则 的值为 .
三、解答题( 共48分 )
13.(14 分)如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点都在格点上,其坐标分别为A(-4,—4),B(6,-6),C(0,-2).
(1)请以点 O 为位似中心,画出符合条件的△ABC的所有位似图形,使之与△ABC的相似比为1: 2.
(2)△ABC内一点P(m,n),经过如此位似变化后,对应点的坐标是 .
14.(16 分)乐乐去西安旅游时当他看见宏伟的古城墙后,他想要测量城墙的高度.如图,他拿着一根笔直的小棍
BC,站在距城墙约 30米的点 N处(即 EN=30米),把手臂向前伸直且让小棍 BC竖直,BC∥DE,乐乐看到点 B 和城墙顶端 D 在一条直线上,点C 和底端 E 在一条直线上.已知乐乐的臂长 CM约为 60厘米,小棍 BC 的长为 24 厘米,AN⊥EN,CM⊥AN,DE⊥EN,求城墙的高度 DE.
15.(18 分)如图,四边形 ABCD 为菱形,M 为BC上一点,连接AM交对角线 BD于点G,并且∠ABC=2∠BAM.
(1)求证:AG=BG;
(2)若 M 为 BC 的中点,S△BGM=1,求△ADG 的面积.
7 相似三角形的性质
测素质
一、1. C 【点拨】∵四边形. ABCD是平行四边形,∴DC∥AB,CD=AB.∴易得△CEF∽△ABF.∵DE:CE=1:2,∴EC:DC=EC:AB=2:3.∴△CEF与△ABF的周长比为2:3.故选 C.
2. C 【点拨】由题意可得五边形 ABCDE 与五边形A B C D E 的相似比为1:3,
即C D :CD=3:1.故选 C.
3. B 【点拨】由已知条件可知 又因为∠B=∠B,所以△EBD∽△ABC.所以 故选 B.
4. C
5. D 【点拨】示意图如图所示.
由题意可得AB∥EF,
∴∠DAB=∠DEF,∠ABD=∠EFD.
∴△DAB∽△DEF.
∴EF=0.9米,即捣头点E上升了0.9米.故选 D.
6. B
7. C 【点拨】在 Rt△AOB中,
同理
同理
由位似图形的概念可知,△GOH 与△AOB 位似,且相似比为
故选 C.
8. A 【点拨】如图,由A,B,C三种直角三角形相似,设C与 B, B 与 A 的 相 似 比 为 k, EF = m, 则 GH = mk,FH=mk .
∴EH=m(1+k ),
FK= km(1+k ).
由题意得
整理得
或 (舍去).
∴这个矩形的面积:
故选 A.
二、9.(3,1)
10.100m和40cm 【点拨】∵两个相似三角形的相似比为 ∴它们的周长比
∴可设较大三角形的周长为 5x cm,则较小三角形的周长为 2x cm.
∵它们的周长之差为60cm,∴5x-2x=60,解得x=20.
∴这两个三角形的周长分别为 100 cm 和40 cm.
11.4.5 【点拨】∵AC=BC=16,∴∠A=∠B.
由折叠的性质可得∠B=∠B',∴∠A=∠B'.
又∵∠AFD=∠B'FG,∴△AFD∽△B'FG.
即 解得 GF=3.5.
∴CG=AC-AF-GF=4.5.
12.5 【 点拨 】如图,过点 D 作 DF⊥AB 于点 F,则∠AFD=90°,
∴∠C=∠AFD=90°.
∵∠ACB=90°,AC=3,BC=1,
∵将△ABC绕点 A 逆时针方向旋转90°得到△AB'C',
∴△ABB'是等腰直角三角形..
又∵DF⊥AB,∴∠FDB=45°.
∴△DFB是等腰直角三角形.∴DF=BF.
∵∠C=∠AFD=90°,∠CAB=∠FAD,
∴△AFD∽△ACB.
即DF =AF .∴AF=3DF.
又∵
三、13.【解】(1)如图所示,△A B C ,△A B C 为所求.
或
14.【解】如图,过点 A 作AH⊥DE 于点 H,交 BC于点G.
则AG=CM=60厘米=0.6米,AH=NE=30米.
由题意得BC=24厘米=0.24米,BC∥DE,
∴∠ABC=∠ADE,∠ACB=∠AED.
∴△ABC∽△ADE.
即 解得 DE=12米.
因此,城墙的高度 DE 为12米.
15.(1)【证明】∵四边形ABCD为菱形,∴BD平分∠ABC.
∴∠ABC=2∠ABG.
又∵∠ABC=2∠BAM,∴∠BAG=∠ABG.
∴AG=BG.
(2)【解】∵四边形ABCD为菱形,∴AD∥BC,AD=BC.
∴∠GAD=∠GMB.
又∵∠AGD=∠BGM,∴△BGM∽△DGA.
∵M为BC的中点,
∴△BGM与△DGA的相似比为1: 2.
相似三角形的性质及应用
[时间: 60分钟 分值:100分]
一、选择题(每题 4分,共32分)
1.如图,在 ABCD 中,点 E 在 CD 上,若 DE :CE=1:2,则△CEF与△ABF的周长比为( )
A.1: 2 B.1 : 3 C.2 : 3 D.4: 9
2. 如图,点 O 是 五 边 形 ABCDE 和 五 边 形A B C D E 的位似中心,若 OA :OA ═1:3,则 C D : CD等于 ( )
A.1 : 2 B.1 : 3 C.3 : 1 D.4 : 1
3.如图,在△ABC中,D,E分别为线段 BC,BA的中点,设△ABC 的面积为 S ,△EBD 的面积为S ,则 ( )
A B C D
4.如图,在平面直角坐标系中,以原点 O为位似中心,若A 点的坐标为(1,2),C点的坐标为(2,4), 则线段CD的长为 ( )
A.2 B.4 C. D
5. 如图为农村一古老的捣碎器,已知支撑柱AB的高为0.5米,踏板 DE的长为1.8米,支撑点 A 到踏脚点 D 的距离为1米,原来捣头点E着地,现在踏脚点 D着地,则捣头点 E 上升了 ( )
A.1.5 米 B.1.2 米 C.1 米 D.0.9 米
6. 如图,点 A,B都在格点上,若 则 AC的长为 ( )
A C.
7.由12个有公共顶点 O的直角三角形拼成如图所示的图形.∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB =1,则图中与△AOB位似的三角形的面积为 ( )
D.
8.如图是一个由A,B,C三种相似的直角三角形纸片(C与B,B与A的相似比相同)拼成的矩形,相邻纸片之间互不重叠也无缝隙,其中A,B,C的纸片的面积分别 S ,S ,S ,若 S > ,则这个矩形的面积一定可以表示为
( )
A.4S B.6S
二、填空题(每题5分,共20分)
9.如图,在平面直角坐标系中,△ABC与△A B C 位似,原点 O是位似中心,且 3.若A(9,3),则 A 的坐标是 .
10.如果两个相似三角形的最长边分别是 35 cm和14 cm,它们的周长之差为 60 cm,那么这两个三角形的周长分别是 .
11.如图,在△ABC中,AC=BC=16,点 D在AB上,点 E 在BC上,点B关于直线DE 的轴对称点为点 B',连接DB',EB',分别与AC相交于F 点,G点,若AF=8,DF=7,B'F=4,,则CG的长度为 .
12.如图,在 Rt△ABC中,∠C=90°,AC=3,BC=1,将△ABC 绕点 A 逆时针方向旋转90°,得到△AB'C'.连接 BB',交AC于点 D,则 的值为 .
三、解答题( 共48分 )
13.(14 分)如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点都在格点上,其坐标分别为A(-4,—4),B(6,-6),C(0,-2).
(1)请以点 O 为位似中心,画出符合条件的△ABC的所有位似图形,使之与△ABC的相似比为1: 2.
(2)△ABC内一点P(m,n),经过如此位似变化后,对应点的坐标是 .
14.(16 分)乐乐去西安旅游时当他看见宏伟的古城墙后,他想要测量城墙的高度.如图,他拿着一根笔直的小棍
BC,站在距城墙约 30米的点 N处(即 EN=30米),把手臂向前伸直且让小棍 BC竖直,BC∥DE,乐乐看到点 B 和城墙顶端 D 在一条直线上,点C 和底端 E 在一条直线上.已知乐乐的臂长 CM约为 60厘米,小棍 BC 的长为 24 厘米,AN⊥EN,CM⊥AN,DE⊥EN,求城墙的高度 DE.
15.(18 分)如图,四边形 ABCD 为菱形,M 为BC上一点,连接AM交对角线 BD于点G,并且∠ABC=2∠BAM.
(1)求证:AG=BG;
(2)若 M 为 BC 的中点,S△BGM=1,求△ADG 的面积.
7 相似三角形的性质
测素质
一、1. C 【点拨】∵四边形. ABCD是平行四边形,∴DC∥AB,CD=AB.∴易得△CEF∽△ABF.∵DE:CE=1:2,∴EC:DC=EC:AB=2:3.∴△CEF与△ABF的周长比为2:3.故选 C.
2. C 【点拨】由题意可得五边形 ABCDE 与五边形A B C D E 的相似比为1:3,
即C D :CD=3:1.故选 C.
3. B 【点拨】由已知条件可知 又因为∠B=∠B,所以△EBD∽△ABC.所以 故选 B.
4. C
5. D 【点拨】示意图如图所示.
由题意可得AB∥EF,
∴∠DAB=∠DEF,∠ABD=∠EFD.
∴△DAB∽△DEF.
∴EF=0.9米,即捣头点E上升了0.9米.故选 D.
6. B
7. C 【点拨】在 Rt△AOB中,
同理
同理
由位似图形的概念可知,△GOH 与△AOB 位似,且相似比为
故选 C.
8. A 【点拨】如图,由A,B,C三种直角三角形相似,设C与 B, B 与 A 的 相 似 比 为 k, EF = m, 则 GH = mk,FH=mk .
∴EH=m(1+k ),
FK= km(1+k ).
由题意得
整理得
或 (舍去).
∴这个矩形的面积:
故选 A.
二、9.(3,1)
10.100m和40cm 【点拨】∵两个相似三角形的相似比为 ∴它们的周长比
∴可设较大三角形的周长为 5x cm,则较小三角形的周长为 2x cm.
∵它们的周长之差为60cm,∴5x-2x=60,解得x=20.
∴这两个三角形的周长分别为 100 cm 和40 cm.
11.4.5 【点拨】∵AC=BC=16,∴∠A=∠B.
由折叠的性质可得∠B=∠B',∴∠A=∠B'.
又∵∠AFD=∠B'FG,∴△AFD∽△B'FG.
即 解得 GF=3.5.
∴CG=AC-AF-GF=4.5.
12.5 【 点拨 】如图,过点 D 作 DF⊥AB 于点 F,则∠AFD=90°,
∴∠C=∠AFD=90°.
∵∠ACB=90°,AC=3,BC=1,
∵将△ABC绕点 A 逆时针方向旋转90°得到△AB'C',
∴△ABB'是等腰直角三角形..
又∵DF⊥AB,∴∠FDB=45°.
∴△DFB是等腰直角三角形.∴DF=BF.
∵∠C=∠AFD=90°,∠CAB=∠FAD,
∴△AFD∽△ACB.
即DF =AF .∴AF=3DF.
又∵
三、13.【解】(1)如图所示,△A B C ,△A B C 为所求.
或
14.【解】如图,过点 A 作AH⊥DE 于点 H,交 BC于点G.
则AG=CM=60厘米=0.6米,AH=NE=30米.
由题意得BC=24厘米=0.24米,BC∥DE,
∴∠ABC=∠ADE,∠ACB=∠AED.
∴△ABC∽△ADE.
即 解得 DE=12米.
因此,城墙的高度 DE 为12米.
15.(1)【证明】∵四边形ABCD为菱形,∴BD平分∠ABC.
∴∠ABC=2∠ABG.
又∵∠ABC=2∠BAM,∴∠BAG=∠ABG.
∴AG=BG.
(2)【解】∵四边形ABCD为菱形,∴AD∥BC,AD=BC.
∴∠GAD=∠GMB.
又∵∠AGD=∠BGM,∴△BGM∽△DGA.
∵M为BC的中点,
∴△BGM与△DGA的相似比为1: 2.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
