投影与视图 同步练习(含答案) 2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 投影与视图 同步练习(含答案) 2024-2025学年北师大版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 638.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 15:44:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
投影与视图
[时间:60分钟 分值:100分]
一、选择题(每题4分,共32分)
1.下列说法正确的是( )
A.物体在太阳光下产生的投影是物体的正投影
B.正投影一定是平行投影
C.物体在灯光下产生的投影是物体的正投影
D.正投影可能是中心投影
2.新趋势跨学科 唐代李白《日出行》中云:“日出东方隈,似从地底来”.描述的是看日出的景象,意思是太阳从东方升起,似从地底而来,如图所示,此时观测到地平线和太阳所成的视图可能是 ( )
3.小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是 ( )
4.如图,箭头所指的是某陶艺工作室用于垫放陶器的5块相同的耐火砖搭成的几何体,它的主视图是 ( )
5.如图,它是由五个相同的正方体搭成的几何体,这个几何体的主视图是 ( )
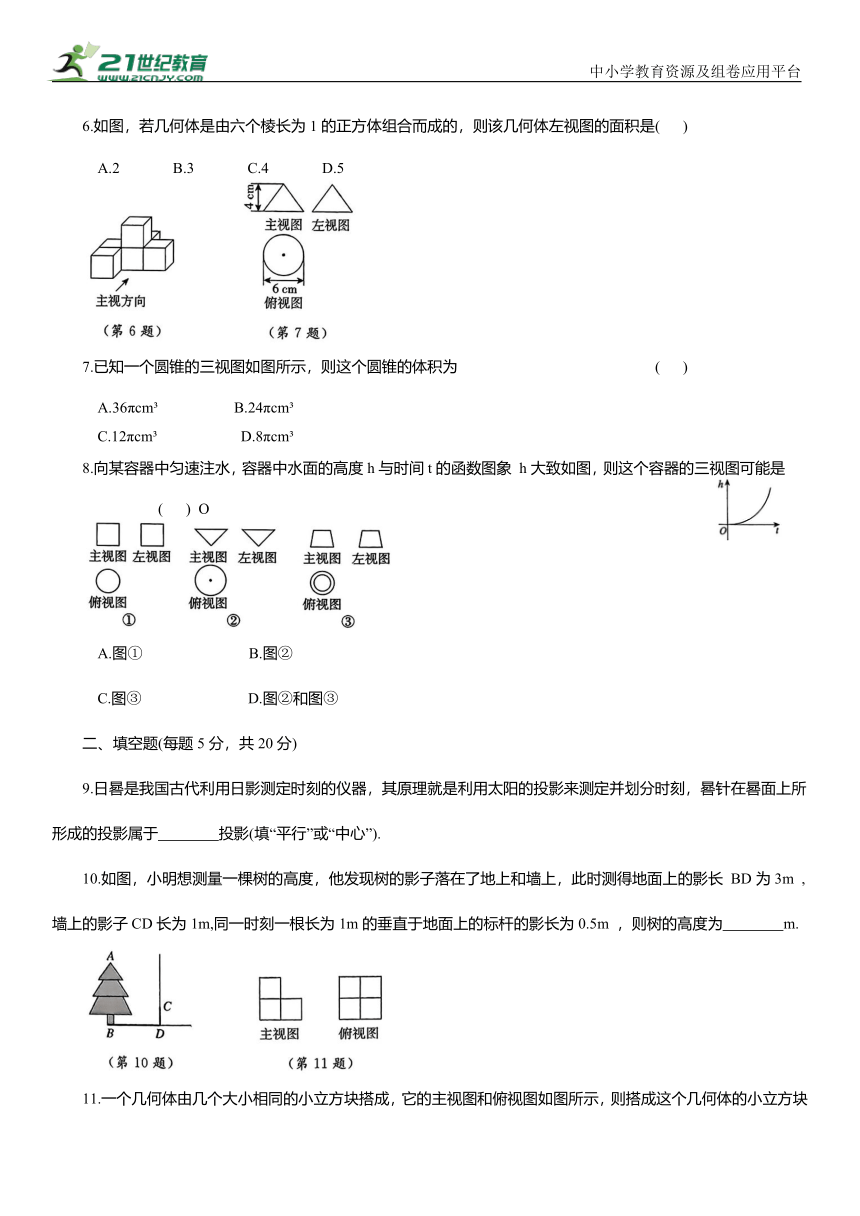
6.如图,若几何体是由六个棱长为1的正方体组合而成的,则该几何体左视图的面积是( )
A.2 B.3 C.4 D.5
7.已知一个圆锥的三视图如图所示,则这个圆锥的体积为 ( )
A.36πcm B.24πcm
C.12πcm D.8πcm
8.向某容器中匀速注水,容器中水面的高度h与时间t的函数图象 h大致如图,则这个容器的三视图可能是 ( ) O
A.图① B.图②
C.图③ D.图②和图③
二、填空题(每题5分,共20分)
9.日晷是我国古代利用日影测定时刻的仪器,其原理就是利用太阳的投影来测定并划分时刻,晷针在晷面上所形成的投影属于 投影(填“平行”或“中心”).
10.如图,小明想测量一棵树的高度,他发现树的影子落在了地上和墙上,此时测得地面上的影长 BD为3m ,墙上的影子CD长为1m,同一时刻一根长为1m的垂直于地面上的标杆的影长为0.5m ,则树的高度为 m.
11.一个几何体由几个大小相同的小立方块搭成,它的主视图和俯视图如图所示,则搭成这个几何体的小立方块最多有 个.
12.如图,长方体的一个底面ABCD 在投影面 P上,M,N分别是侧棱 BF,CG的中点,矩形EFGH与矩形 EMNH 的投影 都 是 矩 形ABCD,设它们的面积分别是 S ,S ,S,则 S ,S ,S的关系是 (用“=”“>”或“<”连接).
三、解答题 ( 共48分 )
13.(12分) 画出如图所示的几何体的三视图.
14(12分)如图,路灯下一墙墩(用线段AB表示)的影子是 BC,小明(用线段DE表示)的影子是EF,在M处有一棵小树,它的影子是 MN.
(1)画出路灯的位置(用点P 表示);
(2)在图中画出表示小树的线段.
15,(12分)一个几何体由大小相同的小正方体搭成,俯视图如图所示,其中小正方形中的数字表示在该位置的小正方体个数.
(1)请画出这个几何体的主视图和左视图.
(2)若小正方体的棱长为2,求该几何体的体积和表面积.
16.(12分) 如图,明明利用家门口路灯的灯光来测量该路灯的高度,明明在 A 处时,亮亮测得明明的影长 AM 为 2米,明明向前走 2 米到B 处时,亮亮测得明明的影长 BM'为1 米,已知明明的身高 AA'(BB')为 1.72米.
(1)求路灯高 CD.
(2)在此路灯下,明明在直线 MC 上运动,明明应由点 A前进或后退多少米,亮亮恰好测得明明的影长是其身高的2倍
一、 1. B
2. B 【点拨】地平线以上的太阳能看见,地平线以下的太阳看不见,根据看得见的轮廓线用实线,看不见的轮廓线用虚线对各选项进行判断.
3. B 【点拨】当等边三角形木框所在面与太阳光平行时,其投影是线段;当等边三角形木框所在面与太阳光有一定角度时,其投影是三角形;无论如何放置都得不到一个点.故选 B.
4. D 5. B
6. C 【点拨】该几何体左视图分上下两层,其中下层有3个正方形,上层中间有1个正方形,共4 个正方形.
∵正方体的棱长为1,∴该几何体左视图的面积为4.故选 C.
7. C 【点拨】观察三视图,得圆锥的底面半径为6÷2=3( cm),高为4 cm,所以圆锥的体积为 故选 C.
8. C 【点拨】分析函数图象可知,注水速度越来越快,所以容器开口越来越小,只有图③符合.故选C.
二、9.平行 10.7 11.6
【点拨】∵立体图形是一个长方体,∴矩形 EFGH的面积等于矩形ABCD的面积,即
∵EF三、13.【解】如图所示.
14.【解】(1)如图,点 P 是路灯的位置.
(2)如图,线段 MG 表示小树.
15.【解】(1)如图所示.
(2)∵小正方体的棱长为2,
∴每个小正方体的体积为2×2×2=8.
∴该几何体的体积为(1+2+1+3+1+4)×8=96.
∵小正方体的棱长为2,
∴每个小正方体的每个面的面积为2×2=4.
∴该几何体的表面积为(12+18+14)×4=176.
【解】(1)由题意知 AA'∥CD,AB=2 米,∴易得△MAA'∽△MCD.
即
同理易得△M'BB'∽△M'CD,
即 由①②可得 BC=2米,CD=5.16米.
∴路灯高CD 为5.16 米.
(2)根据中心投影可得离点光源越远,影长越长,则明明应由点A后退.如图,依题意得 EE'=1.72米,NE=2EE'=3.44 米.
设明明应由点A后退x米,即AE=x米.
依题意易得
解得x=2.88.
∴明明应由点A后退2.88米,亮亮恰好测得明明的影长是其身高的2倍.
投影与视图
[时间:60分钟 分值:100分]
一、选择题(每题4分,共32分)
1.下列说法正确的是( )
A.物体在太阳光下产生的投影是物体的正投影
B.正投影一定是平行投影
C.物体在灯光下产生的投影是物体的正投影
D.正投影可能是中心投影
2.新趋势跨学科 唐代李白《日出行》中云:“日出东方隈,似从地底来”.描述的是看日出的景象,意思是太阳从东方升起,似从地底而来,如图所示,此时观测到地平线和太阳所成的视图可能是 ( )
3.小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是 ( )
4.如图,箭头所指的是某陶艺工作室用于垫放陶器的5块相同的耐火砖搭成的几何体,它的主视图是 ( )
5.如图,它是由五个相同的正方体搭成的几何体,这个几何体的主视图是 ( )
6.如图,若几何体是由六个棱长为1的正方体组合而成的,则该几何体左视图的面积是( )
A.2 B.3 C.4 D.5
7.已知一个圆锥的三视图如图所示,则这个圆锥的体积为 ( )
A.36πcm B.24πcm
C.12πcm D.8πcm
8.向某容器中匀速注水,容器中水面的高度h与时间t的函数图象 h大致如图,则这个容器的三视图可能是 ( ) O
A.图① B.图②
C.图③ D.图②和图③
二、填空题(每题5分,共20分)
9.日晷是我国古代利用日影测定时刻的仪器,其原理就是利用太阳的投影来测定并划分时刻,晷针在晷面上所形成的投影属于 投影(填“平行”或“中心”).
10.如图,小明想测量一棵树的高度,他发现树的影子落在了地上和墙上,此时测得地面上的影长 BD为3m ,墙上的影子CD长为1m,同一时刻一根长为1m的垂直于地面上的标杆的影长为0.5m ,则树的高度为 m.
11.一个几何体由几个大小相同的小立方块搭成,它的主视图和俯视图如图所示,则搭成这个几何体的小立方块最多有 个.
12.如图,长方体的一个底面ABCD 在投影面 P上,M,N分别是侧棱 BF,CG的中点,矩形EFGH与矩形 EMNH 的投影 都 是 矩 形ABCD,设它们的面积分别是 S ,S ,S,则 S ,S ,S的关系是 (用“=”“>”或“<”连接).
三、解答题 ( 共48分 )
13.(12分) 画出如图所示的几何体的三视图.
14(12分)如图,路灯下一墙墩(用线段AB表示)的影子是 BC,小明(用线段DE表示)的影子是EF,在M处有一棵小树,它的影子是 MN.
(1)画出路灯的位置(用点P 表示);
(2)在图中画出表示小树的线段.
15,(12分)一个几何体由大小相同的小正方体搭成,俯视图如图所示,其中小正方形中的数字表示在该位置的小正方体个数.
(1)请画出这个几何体的主视图和左视图.
(2)若小正方体的棱长为2,求该几何体的体积和表面积.
16.(12分) 如图,明明利用家门口路灯的灯光来测量该路灯的高度,明明在 A 处时,亮亮测得明明的影长 AM 为 2米,明明向前走 2 米到B 处时,亮亮测得明明的影长 BM'为1 米,已知明明的身高 AA'(BB')为 1.72米.
(1)求路灯高 CD.
(2)在此路灯下,明明在直线 MC 上运动,明明应由点 A前进或后退多少米,亮亮恰好测得明明的影长是其身高的2倍
一、 1. B
2. B 【点拨】地平线以上的太阳能看见,地平线以下的太阳看不见,根据看得见的轮廓线用实线,看不见的轮廓线用虚线对各选项进行判断.
3. B 【点拨】当等边三角形木框所在面与太阳光平行时,其投影是线段;当等边三角形木框所在面与太阳光有一定角度时,其投影是三角形;无论如何放置都得不到一个点.故选 B.
4. D 5. B
6. C 【点拨】该几何体左视图分上下两层,其中下层有3个正方形,上层中间有1个正方形,共4 个正方形.
∵正方体的棱长为1,∴该几何体左视图的面积为4.故选 C.
7. C 【点拨】观察三视图,得圆锥的底面半径为6÷2=3( cm),高为4 cm,所以圆锥的体积为 故选 C.
8. C 【点拨】分析函数图象可知,注水速度越来越快,所以容器开口越来越小,只有图③符合.故选C.
二、9.平行 10.7 11.6
【点拨】∵立体图形是一个长方体,∴矩形 EFGH的面积等于矩形ABCD的面积,即
∵EF
14.【解】(1)如图,点 P 是路灯的位置.
(2)如图,线段 MG 表示小树.
15.【解】(1)如图所示.
(2)∵小正方体的棱长为2,
∴每个小正方体的体积为2×2×2=8.
∴该几何体的体积为(1+2+1+3+1+4)×8=96.
∵小正方体的棱长为2,
∴每个小正方体的每个面的面积为2×2=4.
∴该几何体的表面积为(12+18+14)×4=176.
【解】(1)由题意知 AA'∥CD,AB=2 米,∴易得△MAA'∽△MCD.
即
同理易得△M'BB'∽△M'CD,
即 由①②可得 BC=2米,CD=5.16米.
∴路灯高CD 为5.16 米.
(2)根据中心投影可得离点光源越远,影长越长,则明明应由点A后退.如图,依题意得 EE'=1.72米,NE=2EE'=3.44 米.
设明明应由点A后退x米,即AE=x米.
依题意易得
解得x=2.88.
∴明明应由点A后退2.88米,亮亮恰好测得明明的影长是其身高的2倍.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
