6.2 反比例函数的图象与性质 同步练习(含答案) 2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 6.2 反比例函数的图象与性质 同步练习(含答案) 2024-2025学年北师大版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 826.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 10:37:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
6.2 反比例函数的图象与性质
反比例函数的图象
基础题目
1.反比例函数 的图象可能是 ( )
2.已知反比例函数 (k≠0)的图象经过点(3,4),则该反比例函数的图象也一定经过点 ( )
B.(2,5)
C.(4,3) D.(2,-3)
3.小明对“保温杯的保温性能”进行实验,分别取①和②两种带有液晶显示的保温杯用于实验,两保温杯中分别倒入质量和初始温度相同的热水,然后置于冷藏箱中,根据实验数据作出水温随时间变化的图象如图所示,下面说法错误的是 ( )
A.两图象均不是反比例函数图象
B.5 min时,①号保温杯中水的温度较高
C.8 min时,②号保温杯中水的温度约是 20℃
D.②号保温杯比①号保温杯的保温性能好
4.已知反比例函数 的图象经过点(a,7),则a的值为 .
5.已知反比例函数 的图象经过点(--3,--2),则k= ,此图象位于第 象限内.
6.反比例函数 的图象分布情况如图所示,则k的值可以是 (写出一个符合条件的k值即可).
综合应用题
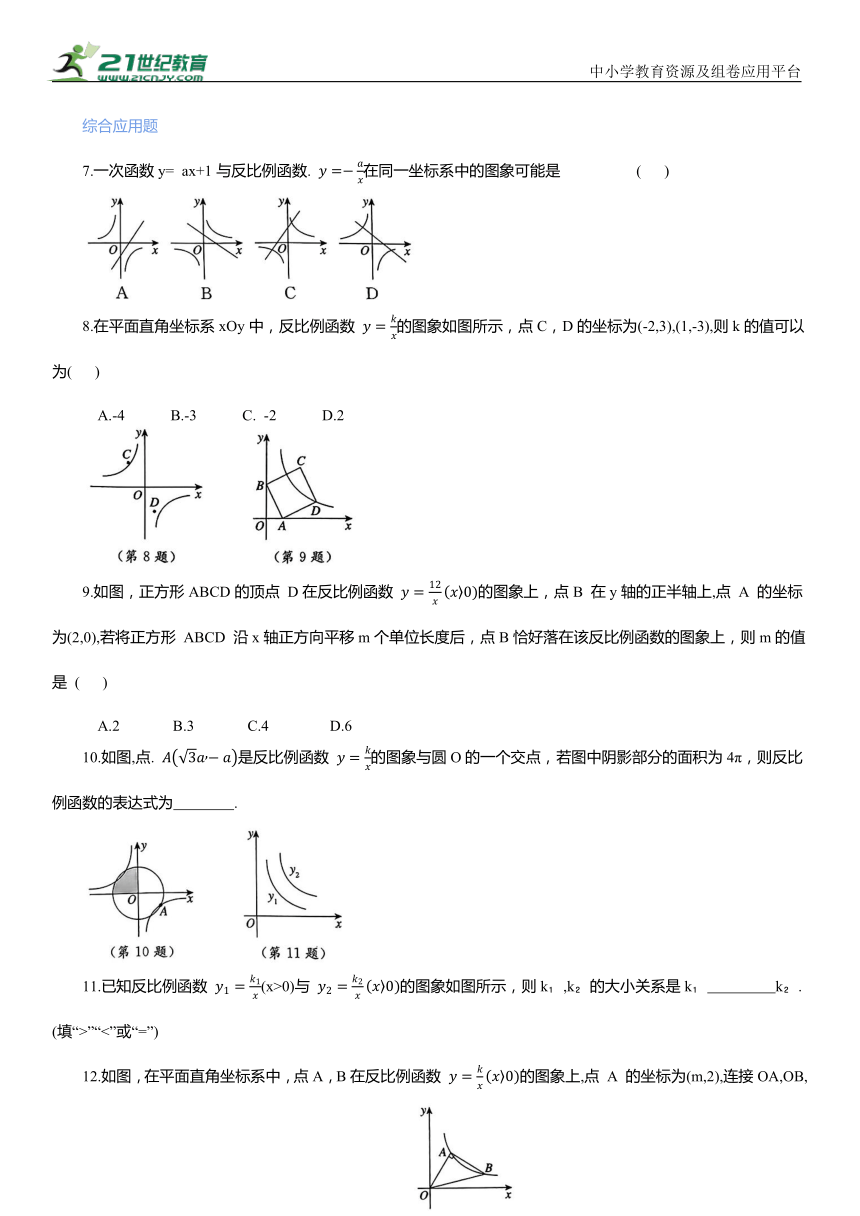
7.一次函数y= ax+1与反比例函数. 在同一坐标系中的图象可能是 ( )
8.在平面直角坐标系xOy中,反比例函数 的图象如图所示,点C,D的坐标为(-2,3),(1,-3),则k的值可以为( )
A.-4 B.-3 C. -2 D.2
9.如图,正方形ABCD的顶点 D在反比例函数 的图象上,点B 在y轴的正半轴上,点 A 的坐标为(2,0),若将正方形 ABCD 沿x轴正方向平移m个单位长度后,点B恰好落在该反比例函数的图象上,则m的值是 ( )
A.2 B.3 C.4 D.6
10.如图,点. 是反比例函数 的图象与圆O的一个交点,若图中阴影部分的面积为4π,则反比例函数的表达式为 .
11.已知反比例函数 (x>0)与 的图象如图所示,则k ,k 的大小关系是k k .(填“>”“<”或“=”)
12.如图,在平面直角坐标系中,点A,B在反比例函数 的图象上,点 A 的坐标为(m,2),连接OA,OB,AB.若OA=AB,∠OAB = 90°, 则 k 的 值为 .
13.已知反比例函数 的图象的一支如图所示,它经过点(3,-2).
(1)求这个反比例函数的表达式,并补画该函数图象的另一支;
(2)当y≤5,且 y≠0时,求自变量x的取值范围.
创新拓展题
14.已知反比例函数 (m为常数)的图象位于第一、三象限内.
(1)求m的取值范围.
(2)如图,若该反比例函数的图象经过平行四边形 ABOD 的顶点 D,点A,B的坐标分别为(0,5),(-3,0).
①求反比例函数的表达式.
②设点 P 是该反比例函数图象上的一点,若OD=OP,则点 P 的坐标为 ;若以D,O,P为顶点的三角形是等腰三角形,则满足条件的点 P 有 个.
反比例函数的性质
基础题目
1 下列函数中,函数值 y 随x的增大而减小的是 ( )
A. y=6x B. y=-6x
2.下列关于反比例函数y= 结论正确的是 ( )
A.图象必经过点(2,4)
B.图象在一、三象限内
C. y随x的增大而增大
D.图象关于原点中心对称
3. 若点 A(—3,y ),B(—1,y )都在反比例函数 的图象上,则 y y (填“>”或“<”).
4.如图,P为反比例函数 图象上的一点,过点 P 作 PA⊥y轴,垂足为点A.若△PAO的面积为4,则k=
5.若反比例函数 当x<0时,y随x 的增大而增大,则k的取值范围是 .
6.已知反比例函数的图象如图所示.
(1)k的值是 ;
(2)点 B(-2,4) 这个函数的图象上;(填“在”或“不在”)
(3)在第二象限内,y随x 的增大而 .(填“增大”或“减小”)
综合应用题
7.已知反比例函数 的图象经过平移后可以得到函数 的图象,关于新函数 下列结论正确的是( )
A.当x>0时,y随x的增大而增大
B.该函数的图象与 y轴有交点
C.该函数图象与 x轴的交点为(1,0)
D.当 时,y的取值范围是08.如图,正方形四个顶点分别位于两个反比例函数 和 的图象的四个分支上,则实数n的值为 ( )
A.—3 C D.3
9.如图,矩形OABC与反比例函数 是非零常数,x>0)的图象交于点M,N,与反比例函数 是非零常数,x>0)的图象交于点 B,连接OM,ON.若四边形 OMBN 的面积为3,则 ( )
A.3 B.-3 C
10.如图,正方形ABCD的顶点分别在反比例函数 和 的图象上.若 BD∥y轴,点 D 的横坐标为3,则
A.36 B.18
C.12 D.9
11.对于平面直角坐标系xOy中的图形 M 和直线 m,给出如下定义:若图形M上有一点到直线m的距离为d,则称这个点为图形M到直线m的“d距点”.如图,双曲线C: 和直线 l:y=-x+n,若双曲线 C到直线 l 的‘ 距点”只有2个,则n的取值范围是 .
创新拓展题
12. 新考法 分类讨论法 设 函数 (k>0).
(1)当2≤x≤3时,函数y 的最大值是a,函数y 的最小值是a-4,求a和k 的值.
(2)设m≠0,且m≠-1,当x=m时, 当x=m+1时, .圆圆说:“p一定大于q”.你认为圆圆的说法正确吗 为什么
2 反比例函数的图象与性质
第1课时 反比例函数的图象
1. C 2. C 3. D 4.2 5.6;一、三
6.1(答案不唯一) 7. B 8. A
9. B 【点拨】如图所示,过点 D作DF⊥x轴于点 F.∵A(2,0),∴OA=2.
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°.
∴∠BAO+∠DAF=90°.
∵DF⊥x轴,∴∠DFA=90°.
∴∠DAF+∠ADF=90°.
∴∠BAO=∠ADF.
又∵∠AOB=∠DFA=90°,
∴△AOB≌△DFA(AAS).
∴DF=AO=2,OB=AF.
∵点 D在反比例函数 的图象上,
∴点 D 的坐标为(6,2).
∴OF=6.
∴OB=AF=4.
∴B(0,4).
∵将正方形ABCD 沿x轴正方向平移m个单位长度后,点 B 恰好落在该反比例函数的图象上,
∴4m=12,解得m=3.
故选 B.
【点拨】如图所示,过点 A作AD⊥y轴于点D,过点 B作BC⊥DA交DA 的延长线于点C,则∠C=∠CDO=90°.
∵∠OAB=90°,
∠CBA.
又∵OA=AB,∴△DAO≌△CBA.
∴DA=CB,AC=OD.
∵点 A的坐标为(m,2),
∴AC=OD=2,BC=AD=m.
∴易得B(2+m,2-m).
∵点 A,B在反比例函数 的图象上,
∴2m=(2+m)(2-m),
解得 或 (舍去).
13.【解】(1)把点(3,-2)的坐标代入 得 解得 k=-6,
∴这个反比例函数的表达式为
补画该函数图象的另一支如图.
(2)当y=5时, 解得 ∴当y≤5,且 y≠0时, 或x>0.
14.【解】(1)根据题意,得1—2m>0,解得
(2)①∵B(-3,0),∴OB=3.
∵四边形ABOD为平行四边形,
∴AD∥OB,AD=OB=3.
∵点A的坐标为(0,5),
∴OA=5.
∴点 D 的坐标为(3,5).
∵点 D在反比例函数 的图象上,
∴1-2m=3×5=15.
∴反比例函数的表达式为
②(-3,-5),(-5,-3),(5,3);4
第2课时 反比例函数的性质
1. B 2. D 3.> 4.-8 5. k<2
6.(1)-2 (2)不在 (3)增大
7. C 【点拨】A.当x>0时,y随x的增大而减小,本选项错误,不符合题意;
B.该函数的图象与y轴无限接近,但是没有交点,故本选项错误,不符合题意;
C.该函数图象与x轴的交点为(1,0),故本选项正确,符合题意;
D.当 时,y的取值范围是y≥1,故本选项错误,不符合题意.
故选 C.
8. A 【点拨】如图,连接正方形ABEF的对角线BF,AE,
易知对角线交于原点O,过点A,B分别作x轴的垂线,垂足分别为C,D.由图知
∵四边形ABEF 是正方形,
∴AO=BO,∠AOB=∠BDO=∠ACO=90°.
∴∠CAO=90°-∠AOC=∠BOD.
∴△AOC≌△OBD(AAS).
即
∵点 A在第二象限内,∴n=-3.故选 A.
9. B 【点拨】∵y ,y 的图象均在第一象限内,
∵点 M,N均在反比例函数 是非零常数,x>0)的图象上,
∵矩形OABC的顶点 B 在反比例函数 是非零常数,x>0)的图象上,
故选 B.
10. B 【点拨】如图,连接AC交 BD 于点E.
∵四边形ABCD是正方形,
∴AE=BE=DE,AC⊥BD.
设AE≈BE≈DE=m(m>0),D(3,ω),
∵BD∥y轴,∴易得B(3,a+2m),A(3+m,a+m).
∵点 A,B都在反比例函数 的图象上,
∴k =3(a+2m)=(3+m)(a+m).
∵m>0,∴m=3-a.∴B(3,6-a).
∵B(3,6-a)在反比例函数 的图象上,D(3,a)在 的图象上,
故选 B.
11.212.【解】(1)x≠3
(2
(3)如图所示.
(4)当x>3时y随x 的增大而减小(答案不唯一)
(5)y13.【解】(1)∵k>0,2≤x≤3,
∴y 随x的增大而减小,y 随x的增大而增大.
∴当x=2时,y 有最大值,最大值为
当x=2时,y 有最小值,最小值为
由①②得a=2,k=4.
(2)圆圆的说法不正确,理由如下:
当x=m时, 当x=m+1时
当m<-1时,
当--1当m>0时,
综上所述,圆圆的说法不正确,
6.2 反比例函数的图象与性质
反比例函数的图象
基础题目
1.反比例函数 的图象可能是 ( )
2.已知反比例函数 (k≠0)的图象经过点(3,4),则该反比例函数的图象也一定经过点 ( )
B.(2,5)
C.(4,3) D.(2,-3)
3.小明对“保温杯的保温性能”进行实验,分别取①和②两种带有液晶显示的保温杯用于实验,两保温杯中分别倒入质量和初始温度相同的热水,然后置于冷藏箱中,根据实验数据作出水温随时间变化的图象如图所示,下面说法错误的是 ( )
A.两图象均不是反比例函数图象
B.5 min时,①号保温杯中水的温度较高
C.8 min时,②号保温杯中水的温度约是 20℃
D.②号保温杯比①号保温杯的保温性能好
4.已知反比例函数 的图象经过点(a,7),则a的值为 .
5.已知反比例函数 的图象经过点(--3,--2),则k= ,此图象位于第 象限内.
6.反比例函数 的图象分布情况如图所示,则k的值可以是 (写出一个符合条件的k值即可).
综合应用题
7.一次函数y= ax+1与反比例函数. 在同一坐标系中的图象可能是 ( )
8.在平面直角坐标系xOy中,反比例函数 的图象如图所示,点C,D的坐标为(-2,3),(1,-3),则k的值可以为( )
A.-4 B.-3 C. -2 D.2
9.如图,正方形ABCD的顶点 D在反比例函数 的图象上,点B 在y轴的正半轴上,点 A 的坐标为(2,0),若将正方形 ABCD 沿x轴正方向平移m个单位长度后,点B恰好落在该反比例函数的图象上,则m的值是 ( )
A.2 B.3 C.4 D.6
10.如图,点. 是反比例函数 的图象与圆O的一个交点,若图中阴影部分的面积为4π,则反比例函数的表达式为 .
11.已知反比例函数 (x>0)与 的图象如图所示,则k ,k 的大小关系是k k .(填“>”“<”或“=”)
12.如图,在平面直角坐标系中,点A,B在反比例函数 的图象上,点 A 的坐标为(m,2),连接OA,OB,AB.若OA=AB,∠OAB = 90°, 则 k 的 值为 .
13.已知反比例函数 的图象的一支如图所示,它经过点(3,-2).
(1)求这个反比例函数的表达式,并补画该函数图象的另一支;
(2)当y≤5,且 y≠0时,求自变量x的取值范围.
创新拓展题
14.已知反比例函数 (m为常数)的图象位于第一、三象限内.
(1)求m的取值范围.
(2)如图,若该反比例函数的图象经过平行四边形 ABOD 的顶点 D,点A,B的坐标分别为(0,5),(-3,0).
①求反比例函数的表达式.
②设点 P 是该反比例函数图象上的一点,若OD=OP,则点 P 的坐标为 ;若以D,O,P为顶点的三角形是等腰三角形,则满足条件的点 P 有 个.
反比例函数的性质
基础题目
1 下列函数中,函数值 y 随x的增大而减小的是 ( )
A. y=6x B. y=-6x
2.下列关于反比例函数y= 结论正确的是 ( )
A.图象必经过点(2,4)
B.图象在一、三象限内
C. y随x的增大而增大
D.图象关于原点中心对称
3. 若点 A(—3,y ),B(—1,y )都在反比例函数 的图象上,则 y y (填“>”或“<”).
4.如图,P为反比例函数 图象上的一点,过点 P 作 PA⊥y轴,垂足为点A.若△PAO的面积为4,则k=
5.若反比例函数 当x<0时,y随x 的增大而增大,则k的取值范围是 .
6.已知反比例函数的图象如图所示.
(1)k的值是 ;
(2)点 B(-2,4) 这个函数的图象上;(填“在”或“不在”)
(3)在第二象限内,y随x 的增大而 .(填“增大”或“减小”)
综合应用题
7.已知反比例函数 的图象经过平移后可以得到函数 的图象,关于新函数 下列结论正确的是( )
A.当x>0时,y随x的增大而增大
B.该函数的图象与 y轴有交点
C.该函数图象与 x轴的交点为(1,0)
D.当 时,y的取值范围是0
A.—3 C D.3
9.如图,矩形OABC与反比例函数 是非零常数,x>0)的图象交于点M,N,与反比例函数 是非零常数,x>0)的图象交于点 B,连接OM,ON.若四边形 OMBN 的面积为3,则 ( )
A.3 B.-3 C
10.如图,正方形ABCD的顶点分别在反比例函数 和 的图象上.若 BD∥y轴,点 D 的横坐标为3,则
A.36 B.18
C.12 D.9
11.对于平面直角坐标系xOy中的图形 M 和直线 m,给出如下定义:若图形M上有一点到直线m的距离为d,则称这个点为图形M到直线m的“d距点”.如图,双曲线C: 和直线 l:y=-x+n,若双曲线 C到直线 l 的‘ 距点”只有2个,则n的取值范围是 .
创新拓展题
12. 新考法 分类讨论法 设 函数 (k>0).
(1)当2≤x≤3时,函数y 的最大值是a,函数y 的最小值是a-4,求a和k 的值.
(2)设m≠0,且m≠-1,当x=m时, 当x=m+1时, .圆圆说:“p一定大于q”.你认为圆圆的说法正确吗 为什么
2 反比例函数的图象与性质
第1课时 反比例函数的图象
1. C 2. C 3. D 4.2 5.6;一、三
6.1(答案不唯一) 7. B 8. A
9. B 【点拨】如图所示,过点 D作DF⊥x轴于点 F.∵A(2,0),∴OA=2.
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°.
∴∠BAO+∠DAF=90°.
∵DF⊥x轴,∴∠DFA=90°.
∴∠DAF+∠ADF=90°.
∴∠BAO=∠ADF.
又∵∠AOB=∠DFA=90°,
∴△AOB≌△DFA(AAS).
∴DF=AO=2,OB=AF.
∵点 D在反比例函数 的图象上,
∴点 D 的坐标为(6,2).
∴OF=6.
∴OB=AF=4.
∴B(0,4).
∵将正方形ABCD 沿x轴正方向平移m个单位长度后,点 B 恰好落在该反比例函数的图象上,
∴4m=12,解得m=3.
故选 B.
【点拨】如图所示,过点 A作AD⊥y轴于点D,过点 B作BC⊥DA交DA 的延长线于点C,则∠C=∠CDO=90°.
∵∠OAB=90°,
∠CBA.
又∵OA=AB,∴△DAO≌△CBA.
∴DA=CB,AC=OD.
∵点 A的坐标为(m,2),
∴AC=OD=2,BC=AD=m.
∴易得B(2+m,2-m).
∵点 A,B在反比例函数 的图象上,
∴2m=(2+m)(2-m),
解得 或 (舍去).
13.【解】(1)把点(3,-2)的坐标代入 得 解得 k=-6,
∴这个反比例函数的表达式为
补画该函数图象的另一支如图.
(2)当y=5时, 解得 ∴当y≤5,且 y≠0时, 或x>0.
14.【解】(1)根据题意,得1—2m>0,解得
(2)①∵B(-3,0),∴OB=3.
∵四边形ABOD为平行四边形,
∴AD∥OB,AD=OB=3.
∵点A的坐标为(0,5),
∴OA=5.
∴点 D 的坐标为(3,5).
∵点 D在反比例函数 的图象上,
∴1-2m=3×5=15.
∴反比例函数的表达式为
②(-3,-5),(-5,-3),(5,3);4
第2课时 反比例函数的性质
1. B 2. D 3.> 4.-8 5. k<2
6.(1)-2 (2)不在 (3)增大
7. C 【点拨】A.当x>0时,y随x的增大而减小,本选项错误,不符合题意;
B.该函数的图象与y轴无限接近,但是没有交点,故本选项错误,不符合题意;
C.该函数图象与x轴的交点为(1,0),故本选项正确,符合题意;
D.当 时,y的取值范围是y≥1,故本选项错误,不符合题意.
故选 C.
8. A 【点拨】如图,连接正方形ABEF的对角线BF,AE,
易知对角线交于原点O,过点A,B分别作x轴的垂线,垂足分别为C,D.由图知
∵四边形ABEF 是正方形,
∴AO=BO,∠AOB=∠BDO=∠ACO=90°.
∴∠CAO=90°-∠AOC=∠BOD.
∴△AOC≌△OBD(AAS).
即
∵点 A在第二象限内,∴n=-3.故选 A.
9. B 【点拨】∵y ,y 的图象均在第一象限内,
∵点 M,N均在反比例函数 是非零常数,x>0)的图象上,
∵矩形OABC的顶点 B 在反比例函数 是非零常数,x>0)的图象上,
故选 B.
10. B 【点拨】如图,连接AC交 BD 于点E.
∵四边形ABCD是正方形,
∴AE=BE=DE,AC⊥BD.
设AE≈BE≈DE=m(m>0),D(3,ω),
∵BD∥y轴,∴易得B(3,a+2m),A(3+m,a+m).
∵点 A,B都在反比例函数 的图象上,
∴k =3(a+2m)=(3+m)(a+m).
∵m>0,∴m=3-a.∴B(3,6-a).
∵B(3,6-a)在反比例函数 的图象上,D(3,a)在 的图象上,
故选 B.
11.2
(2
(3)如图所示.
(4)当x>3时y随x 的增大而减小(答案不唯一)
(5)y
∴y 随x的增大而减小,y 随x的增大而增大.
∴当x=2时,y 有最大值,最大值为
当x=2时,y 有最小值,最小值为
由①②得a=2,k=4.
(2)圆圆的说法不正确,理由如下:
当x=m时, 当x=m+1时
当m<-1时,
当--1
综上所述,圆圆的说法不正确,
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
