23.3相似三角形——九年级数学华东师大版(2012)上册课前导学(含答案)
文档属性
| 名称 | 23.3相似三角形——九年级数学华东师大版(2012)上册课前导学(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 427.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 10:43:44 | ||
图片预览



文档简介
23.3相似三角形
——九年级数学华东师大版(2012)上册课前导学
一、知识详解
相似三角形的判定
1.在相似多边形中,最简单的就是相似 形.
在与中,如果,,,
且.即三个角分别相等,三条边成比例.我们就说与相似,记作 ,相似比为 .相似用符号“ ”表示,读作“相似于”.
2.平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形 .
3.三边 的两个三角形相似.
符号语言表示:
如图,在和中,
∵ ,
∴.
4.两边 且夹角 的两个三角形相似;
符号语言表示:
如图,在和中,
∵ ,,
∴ .
相似三角形的性质
5.如图, ,相似比为k,和分别是和的高,求证.
证明:∵ ,
∴ .
又和都是直角三角形,
∴ .
∴
由此可得:相似三角形对应高的比等于 .
6.证明相似三角形对应中线的比、对应角平分线的比也等于相似比k.于是得:角形对应高的比、对应中线的比、对应角平分线的比都等于 .
7.相似三角形的面积之比与相似比有什么关系?
证明:若,相似比为k,和分别是和的对应高.
.
二、题目速练
1.如图,,若,,则GF的长为( )
A.2 B.3 C.4 D.1.5
2.如图,在矩形ABCD中,E、F分别是DC、BC边上的点,且,则下列结论正确的是( )
A. B.
C. D.
3.如图所示,给出下列条件:①;②;③;④.其中能够判定的个数为( )
A.1 B.2 C.3 D.4
4.如图,,,BD相交于点E,,,,则BD的长为( )
A. B.4 C. D.6
5.已知,且相似比为,若中BC边上的中线,则中EF边上的中线________.
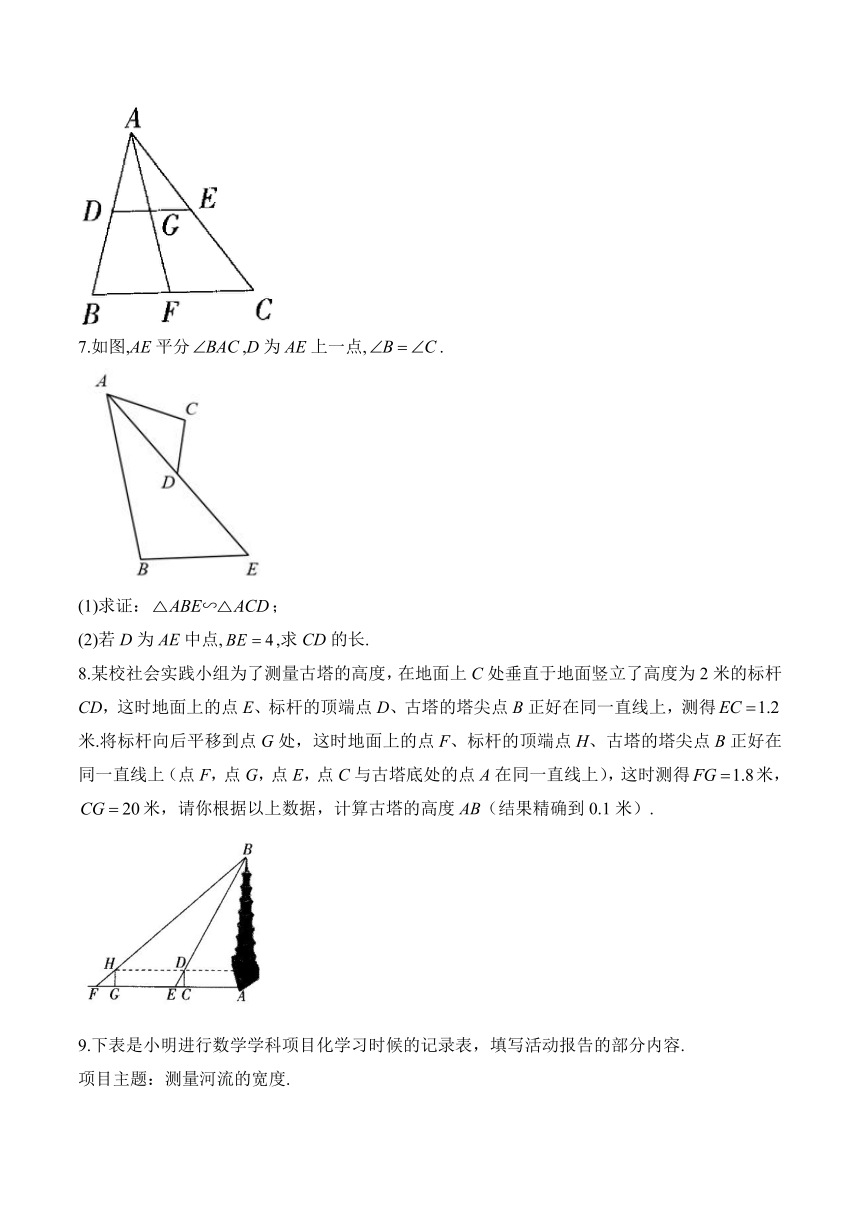
6.如图,已知,且,是的平分线,交DE于点G,交BC于点F,则___________.
7.如图,AE平分,D为AE上一点,.
(1)求证:;
(2)若D为AE中点,,求CD的长.
8.某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E、标杆的顶端点D、古塔的塔尖点B正好在同一直线上,测得米.将标杆向后平移到点G处,这时地面上的点F、标杆的顶端点H、古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得米,米,请你根据以上数据,计算古塔的高度AB(结果精确到0.1米).
9.下表是小明进行数学学科项目化学习时候的记录表,填写活动报告的部分内容.
项目主题:测量河流的宽度.
项目探究:河流宽度不能直接测量,需要借助一些工具,比如:小镜子,标杆,皮尺,自制的直角三角形模板…,各组确定方案后,选择测量工具,画出测量示意图,并进行实地测量,得到具体数据,从而计算出河流的宽度.
项目成果:下面是小明进行交流展示的部分测量方案及测量数据:
题目 测量河流宽度
目标示意图
测量数据 ,,
请你参与这个项目学习,并完成下列任务
(1)任务一:请你借助小明的测量数据,计算河流的宽度;
(2)任务二:请你写出这个方案中求河流的宽度时用的数学知识______(定出一条即可);
(3)任务三:请你再设计一个与小明不同的测量方案,并画图简要说明一下。
答案及解析
一、知识详解
1.三角;;;
2.相似
3.成比例
4.成比例;相等
5.;;相似比
6.相似比
7.
二、题目速练
1.答案:B
解析:∵,
∴,
∴,即点G为DB的中点,
∵,点G为DB的中点,
∴,
故选:B.
2.答案:C
解析:四边形ABCD是矩形,,又,
即;
,
.
故选:C.
3.答案:C
解析:有三个.
①,再加上为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
②,再加上为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
③中不是已知的比例线段的夹角,不正确
④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定;
故选:C.
4.答案:C
解析:,,,即,,.故选C.
5.答案:6
解析:由相似三角形对应中线的比等于相似比可得,即,.
6.答案:1
解析:,
,
,,
是的平分线,
,.
7.答案:(1)证明见解析
(2)CD的长为2
解析:(1)证明∵AE平分,
∴,
在与中,
∵,
,
∴;
(2)∵D为AE中点,
∴,
∵,
∴,
∴,
∴CD的长为2.
8.答案:68.7米
解析:根据题意得,,,,.,,,解得米,,米.答:古塔的高度AB约为68.7米.
9.答案:(1)
(2)相似三角形对应边成比例
(3)见解析
解析:(1)由题知,
.
,
又,,,
解得:.
答:河流的宽度为.
(2)由题意得:相似三角形的对应边成比例(答案不唯一,合理即可);
(3)(答案不唯一,合理即可).在河对岸找一个参照物A,站在A的正对面B的位置,沿着河岸向东走一段距离,到达C处,在C处坚立一竹竿,然后继续向东行走到D处,使得,再沿着与河岸垂直的位置行走,当走到与AC共线时停下,位置记为E,这时的长度即表示河流的宽度.
——九年级数学华东师大版(2012)上册课前导学
一、知识详解
相似三角形的判定
1.在相似多边形中,最简单的就是相似 形.
在与中,如果,,,
且.即三个角分别相等,三条边成比例.我们就说与相似,记作 ,相似比为 .相似用符号“ ”表示,读作“相似于”.
2.平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形 .
3.三边 的两个三角形相似.
符号语言表示:
如图,在和中,
∵ ,
∴.
4.两边 且夹角 的两个三角形相似;
符号语言表示:
如图,在和中,
∵ ,,
∴ .
相似三角形的性质
5.如图, ,相似比为k,和分别是和的高,求证.
证明:∵ ,
∴ .
又和都是直角三角形,
∴ .
∴
由此可得:相似三角形对应高的比等于 .
6.证明相似三角形对应中线的比、对应角平分线的比也等于相似比k.于是得:角形对应高的比、对应中线的比、对应角平分线的比都等于 .
7.相似三角形的面积之比与相似比有什么关系?
证明:若,相似比为k,和分别是和的对应高.
.
二、题目速练
1.如图,,若,,则GF的长为( )
A.2 B.3 C.4 D.1.5
2.如图,在矩形ABCD中,E、F分别是DC、BC边上的点,且,则下列结论正确的是( )
A. B.
C. D.
3.如图所示,给出下列条件:①;②;③;④.其中能够判定的个数为( )
A.1 B.2 C.3 D.4
4.如图,,,BD相交于点E,,,,则BD的长为( )
A. B.4 C. D.6
5.已知,且相似比为,若中BC边上的中线,则中EF边上的中线________.
6.如图,已知,且,是的平分线,交DE于点G,交BC于点F,则___________.
7.如图,AE平分,D为AE上一点,.
(1)求证:;
(2)若D为AE中点,,求CD的长.
8.某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E、标杆的顶端点D、古塔的塔尖点B正好在同一直线上,测得米.将标杆向后平移到点G处,这时地面上的点F、标杆的顶端点H、古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得米,米,请你根据以上数据,计算古塔的高度AB(结果精确到0.1米).
9.下表是小明进行数学学科项目化学习时候的记录表,填写活动报告的部分内容.
项目主题:测量河流的宽度.
项目探究:河流宽度不能直接测量,需要借助一些工具,比如:小镜子,标杆,皮尺,自制的直角三角形模板…,各组确定方案后,选择测量工具,画出测量示意图,并进行实地测量,得到具体数据,从而计算出河流的宽度.
项目成果:下面是小明进行交流展示的部分测量方案及测量数据:
题目 测量河流宽度
目标示意图
测量数据 ,,
请你参与这个项目学习,并完成下列任务
(1)任务一:请你借助小明的测量数据,计算河流的宽度;
(2)任务二:请你写出这个方案中求河流的宽度时用的数学知识______(定出一条即可);
(3)任务三:请你再设计一个与小明不同的测量方案,并画图简要说明一下。
答案及解析
一、知识详解
1.三角;;;
2.相似
3.成比例
4.成比例;相等
5.;;相似比
6.相似比
7.
二、题目速练
1.答案:B
解析:∵,
∴,
∴,即点G为DB的中点,
∵,点G为DB的中点,
∴,
故选:B.
2.答案:C
解析:四边形ABCD是矩形,,又,
即;
,
.
故选:C.
3.答案:C
解析:有三个.
①,再加上为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
②,再加上为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
③中不是已知的比例线段的夹角,不正确
④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定;
故选:C.
4.答案:C
解析:,,,即,,.故选C.
5.答案:6
解析:由相似三角形对应中线的比等于相似比可得,即,.
6.答案:1
解析:,
,
,,
是的平分线,
,.
7.答案:(1)证明见解析
(2)CD的长为2
解析:(1)证明∵AE平分,
∴,
在与中,
∵,
,
∴;
(2)∵D为AE中点,
∴,
∵,
∴,
∴,
∴CD的长为2.
8.答案:68.7米
解析:根据题意得,,,,.,,,解得米,,米.答:古塔的高度AB约为68.7米.
9.答案:(1)
(2)相似三角形对应边成比例
(3)见解析
解析:(1)由题知,
.
,
又,,,
解得:.
答:河流的宽度为.
(2)由题意得:相似三角形的对应边成比例(答案不唯一,合理即可);
(3)(答案不唯一,合理即可).在河对岸找一个参照物A,站在A的正对面B的位置,沿着河岸向东走一段距离,到达C处,在C处坚立一竹竿,然后继续向东行走到D处,使得,再沿着与河岸垂直的位置行走,当走到与AC共线时停下,位置记为E,这时的长度即表示河流的宽度.
