人教版九年级数学上册第二十四章圆单元测试卷(含解析)
文档属性
| 名称 | 人教版九年级数学上册第二十四章圆单元测试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-27 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级数学上册
第二十四章圆单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
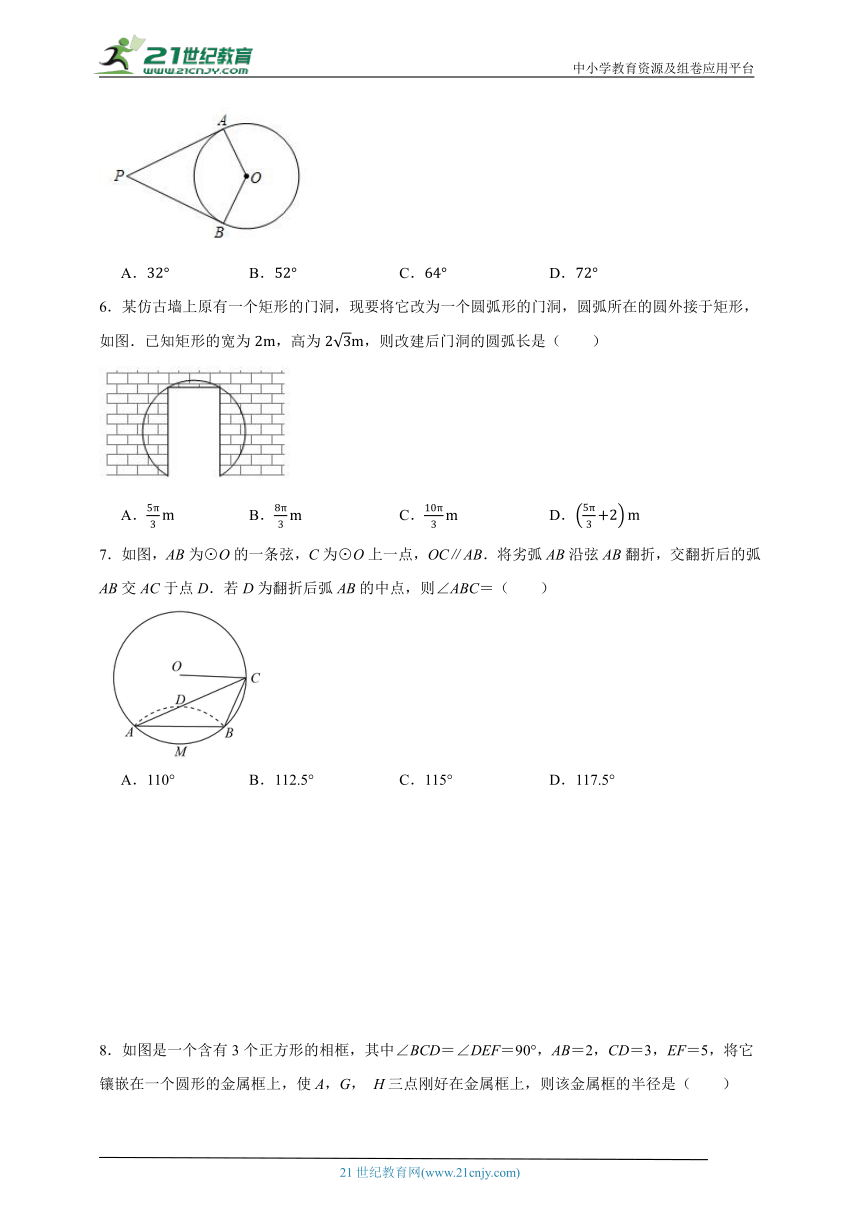
1.已知的半径为3,点O到直线m的距离为d,若直线m与公共点的个数为2个,则d可取( )
A.0 B.3 C.3.5 D.4
2.已知的半径等于5,圆心到直线的距离为4,那么直线与的公共点的个数是( )
A.0 B.1 C.2 D.无法确定
3.已知如图,点为扇形弧上一动点,,,过点作,,的内心为,设,若点运动时,使得,则点的运动路径长为( )
A. B. C. D.
4.如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为( )
A.π B.π C.π D.π
5.如图,PA,PB是的切线,A、B为切点,若,则的度数为( )
A. B. C. D.
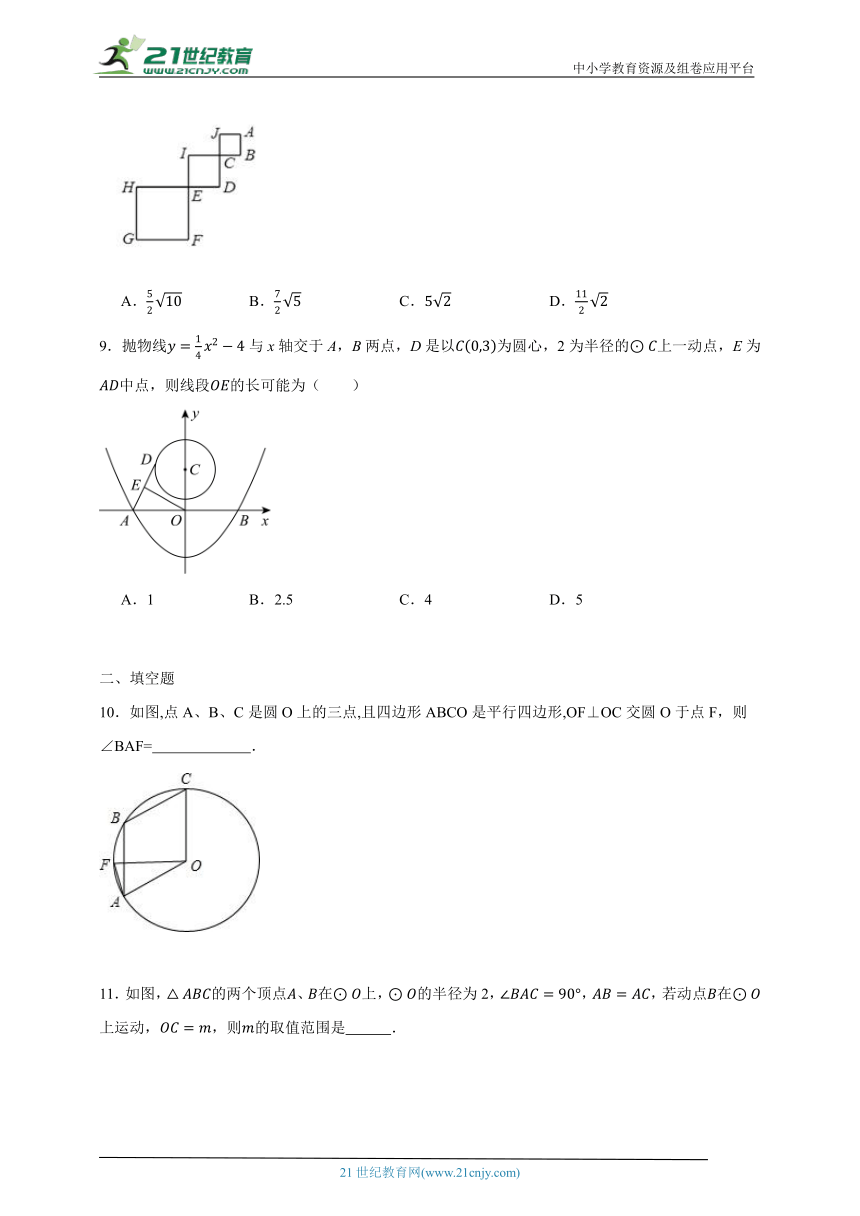
6.某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为,高为,则改建后门洞的圆弧长是( )
A. B. C. D.
7.如图,AB为⊙O的一条弦,C为⊙O上一点,OC∥AB.将劣弧AB沿弦AB翻折,交翻折后的弧AB交AC于点D.若D为翻折后弧AB的中点,则∠ABC=( )
A.110° B.112.5° C.115° D.117.5°
8.如图是一个含有3个正方形的相框,其中∠BCD=∠DEF=90°,AB=2,CD=3,EF=5,将它镶嵌在一个圆形的金属框上,使A,G, H三点刚好在金属框上,则该金属框的半径是( )
A. B. C. D.
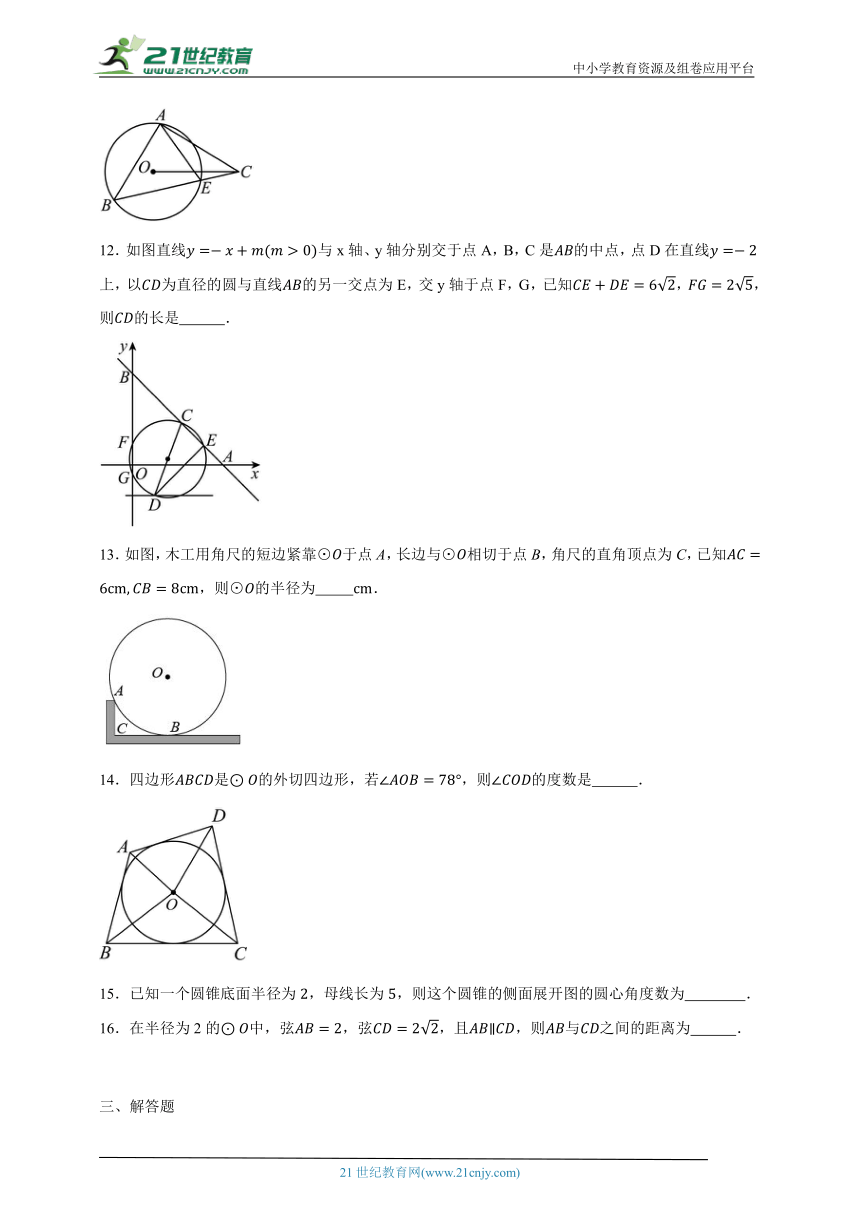
9.抛物线与x轴交于A,B两点,D是以为圆心,2为半径的上一动点,E为中点,则线段的长可能为( )
A.1 B.2.5 C.4 D.5
二、填空题
10.如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF= .
11.如图,的两个顶点、在上,的半径为2,,,若动点在上运动,,则的取值范围是 .
12.如图直线与x轴、y轴分别交于点A,B,C是的中点,点D在直线上,以为直径的圆与直线的另一交点为E,交y轴于点F,G,已知,,则的长是 .
13.如图,木工用角尺的短边紧靠⊙于点A,长边与⊙相切于点B,角尺的直角顶点为C,已知,则⊙的半径为 .
14.四边形是的外切四边形,若,则的度数是 .
15.已知一个圆锥底面半径为,母线长为,则这个圆锥的侧面展开图的圆心角度数为 .
16.在半径为2的中,弦,弦,且,则与之间的距离为 .
三、解答题
17.如图,C是圆O被直径分成的半圆上一点,过点C作圆O的切线交AB的延长线于点P,连接.
(1)若,求的度数
(2)在(1)的条件下,若,求图中阴影部分的面积(结果保留和根号).
18.如图,点是的内心,的延长线和的外接圆交于点.
(1)如图1,连接,求证:;
(2)如图2,若,求证:.
19.如图,在等腰中,,以为直径的与交于点D,,垂足为E,的延长线与的延长线交于点F.
(1)求证:是的切线;
(2)若的半径为,,求的长.
20.如图,是以为直径的半圆上的两点,,连结.
(1)求证:.
(2)若,,求阴影部分的面积.
21.如图,A,P,B,C是⊙O上的四点,∠APC=∠CPB=60°.
(1)判断△ABC的形状,并证明你的结论;
(2)求证:PA+PB=PC.
22.菱形的顶点B,C,D在上,O在线段上.
(1)如图1,若是的切线,求的大小;
(2)如图2,若,,与交于点E,求的长.
23.如图,在正方形网格中,每个小正方形的顶点称为格点. B,C为格点,以线段为直径的交纵向格线于A点,连接. 仅用无刻度的直尺在给定网格中按要求作图,画图过程用虚线表示,画图结果用实线表示.
(1)在图1中作出圆心O;
(2)在图1中作平分交于D点:
(3)在图1中作绕D点顺时针旋转后的线段;
(4)在图2的中作弦.
24.如图,是的直径,是的弦,,垂足为,为上一点,且,连接交于点,连接.
(1)求证:;
(2)若,,求的长.
25.抛物线y=ax2+2x+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C(0,3),点D(m,3)在抛物线上.
(1)求抛物线的解析式;
(2)如图1,连接BC、BD,点P在对称轴左侧的抛物线上,若∠PBC=∠DBC,求点P的坐标;
(3)如图2,点Q为第四象限抛物线上一点,经过C、D、Q三点作⊙M,⊙M的弦QF∥y轴,求证:点F在定直线上.
参考答案:
1.A
【分析】本题考查了直线与圆的位置关系,当时,直线与圆相离,当时,直线与圆相切,当时,直线与圆相交,据此即可解答.
【详解】解:∵直线m与公共点的个数为2个,
∴直线m与相交,
∴,
故选:A
2.C
【分析】利用直线与圆的位置关系的判断方法得到直线与相交,然后根据相离的定义对各选项进行判断.
【详解】 的的半径为5,圆心到直线的距离为4,
圆心到直线的距离小于半径,
直线与相交,
直线与有2个公共点.
故选:C.
【点睛】本题考查了直线与圆的位置关系:设的半径为,圆心到直线的距离为,则当直线与相交 ;当直线与相切 ;当直线与相离 ;熟练掌握直线与圆的位置关系是解本题的关键.
3.A
【分析】连接交分别为,连接,证明在线段上运动,根据,得出两个端点,进而根据对称性可得是等腰直角三角形,根据含30度角的直角三角形的性质得出的长,根据直角三角形斜边上的中线等于斜边的一半,求得的长,进而即可求解.
【详解】解:如图,连接交分别为,连接,
∵,,
∴
∵,
∴,,
∴,
∴是等边三角形,
∵的内心为,
∴,
设,
则,,
∵的内心为,
∴
∴
∴
∴,
∴在上运动,
∵,如图,当时,重合,
则
当时,如图,
同理可得,
∴,
根据对称性可得是等腰直角三角形,
过点作于点,如图,
∴在中,,,,
∴在中,.
即点的运动路径长为.
故选:A.
【点睛】本题考查了等边三角形的性质与判定,三角形内心的性质,找到点的运动轨迹是解题的关键.
4.A
【详解】∵AB=5,AC=3,BC=4,∴△ABC为直角三角形.由题意得S△AED=S△ABC,由图形可知S阴影=S△AED+S扇形ADB-S△ABC,∴S阴影=S扇形ADB==π,故选A.
5.B
【分析】根据切线的性质以及四边形的内角和即可求解.
【详解】解:∵PA,PB是的切线,
∴,
,
,
则 ,
故选B.
【点睛】本题考查了切线的性质以及四边形的内角和,掌握切线的性质是解题的关键.
6.C
【分析】利用勾股定理先求得圆弧形的门洞的直径BC,再利用矩形的性质证得是等边三角形,得到,进而求得门洞的圆弧所对的圆心角为,利用弧长公式即可求解.
【详解】如图,连接,,交于点,
∵ ,
∴是直径,
∴,
∵四边形是矩形,
∴,
∵,
∴,
∴是等边三角形,
∴,
∴门洞的圆弧所对的圆心角为 ,
∴改建后门洞的圆弧长是(m),
故选:C
【点睛】本题考查了弧长公式,矩形的性质以及勾股定理的应用,从实际问题转化为数学模型是解题的关键.
7.B
【分析】如图,取 中点,连接,连接,由题意知,且在一条直线上,,,知,根据圆周角定理,等边对等角,三角形内角和定理等可求,,,,,的值,进而求解的值.
【详解】解:如图,取 中点,连接,连接
由题意知,且在一条直线上,,
∴
∴
∵,
∴
∴
∵
∴
∴
∴
∴
故选B.
【点睛】本题考查了垂径定理,圆周角,等边对等角,三角形内角和定理,折叠性质等知识.解题的关键在于对知识的灵活运用.
8.A
【分析】如图,记过A,G, H三点的圆为则是,的垂直平分线的交点, 记的交点为 的交点为 延长交于 为的垂直平分线,结合正方形的性质可得:再设利用勾股定理建立方程,再解方程即可得到答案.
【详解】解:如图,记过A,G, H三点的圆为则是,的垂直平分线的交点,
记的交点为 的交点为 延长交于 为的垂直平分线,结合正方形的性质可得:
四边形为正方形,则
设 而AB=2,CD=3,EF=5,结合正方形的性质可得:
而
又 而
解得:
故选A
【点睛】本题考查的是正方形的性质,三角形外接圆圆心的确定,圆的基本性质,勾股定理的应用,二次根式的化简,确定过A,G, H三点的圆的圆心是解本题的关键.
9.B
【分析】解一元二次方程可得、,即,再利用勾股定理求得,再根据中位线定理可得,进而即可求解.
【详解】解:连接,
设点、,则、是方程的两个根,
解得,,
∴、,
∴,
∵,
∴,
∵E为中点,O为的中点,
∴是的中位线,
∴,
∵,
即,
∴,
∴的长可能为2.5,
故选:B.
【点睛】本题考查解一元二次方程、勾股定理、三角形中位线定理及三角形的三边关系,熟练掌握角形中位线定理及三角形的三边关系是解题的关键.
10.15°
【分析】根据平行四边形的性质和圆的半径相等得到△AOB为等边三角形,根据等腰三角形的三线合一得到∠BOF=∠AOF=30°,根据圆周角定理计算即可.
【详解】解答:
连接OB,
∵四边形ABCO是平行四边形,∴OC=AB,又OA=OB=OC,
∴OA=OB=AB,∴△AOB为等边三角形.
∵OF⊥OC,OC∥AB,∴OF⊥AB,∴∠BOF=∠AOF=30°.
由圆周角定理得 ,
故答案为15°.
11.
【分析】连接,作,且,连接,,,证明得到,再根据勾股定理求得,然后根据两点之间线段最短求解即可.
【详解】解:如图,连接,作,且,连接,,,
∵,
∴,
在和中,
∴,
∴,
在中,,
根据两点之间线段最短得,
∴,
故答案为:.
【点睛】本题主要考查了圆的有关概念、全等三角形的判定与性质、勾股定理、两点之间线段最短、等角的余角相等,添加辅助线构造全等三角形求解是解答的关键.
12.
【分析】如图,设CD的中点为O′,设直线BA交直线y=﹣2于M,直线y=﹣2交y轴于P,作CH⊥OB于H,连接O′F,作AJ⊥DM于J,O′N⊥FG于N.首先利用等腰直角三角形的性质和条件可确定A,B,C的坐标,再设D(m,﹣2),进而可得O′N与O′F的长,而FN=,然后在Rt△O′FN中利用勾股定理构建方程即可求出m,问题即得解决.
【详解】解:如图,设CD的中点为O′,设直线BA交直线y=﹣2于M,直线y=﹣2交y轴于P,作CH⊥OB于H,连接O′F,作AJ⊥DM于J,O′N⊥FG于N.
∵CD是⊙O′的直径,∴∠CED=90°,
∵直线y=﹣x+m(m>0)与x轴、y轴分别交于点A,B,
∴A(m,0),B(0,m),
∴OA=OB,∴∠OAB=45°,
∵OA∥DM,∴∠EMD=∠OAB=45°,
∵∠DEM=90°,∴ED=EM,
∴EC+ED=EC+EM=CM=,
∵JA⊥DM,∴∠AJM=90°,
∴AJ=JM=2,AM=2,
∴BC=CA=4,∴AB=8,∴BO=AO=8,
∴A(8,0),B(0,8),C(4,4),
设D(m,﹣2),则O′((m+4),1),
∴O′N=(m+4),O′F=CD=,
∵O′N⊥FG,∴FN=,
在Rt△O′FN中,由勾股定理,得:,解得m=1,
∴CD=.
故答案为:.
【点睛】本题考查了圆周角定理、等腰直角三角形的判定和性质、勾股定理、垂径定理、一次函数与坐标轴的交点和两点间的距离等知识,解题的关键是添加常用辅助线构造特殊三角形解决问题,具有相当难度,属于中考填空题中的压轴题.
13./
【分析】设圆的半径为rcm,连接OB、OA,过点A作AD⊥OB,垂足为D,利用勾股定理,在Rt△AOD中,得到r2=(r 6)2+82,求出r即可.
【详解】解:连接OB、OA,过点A作AD⊥OB,垂足为D,如图所示:
∵CB与相切于点B,
∴,
∴,
∴四边形ACBD为矩形,
∴,,
设圆的半径为rcm,在Rt△AOD中,根据勾股定理可得:,
即r2=(r 6)2+82,
解得:,
即的半径为.
故答案为:.
【点睛】本题主要考查了切线的性质,矩形的判定和性质,勾股定理,作出辅助线,构造直角三角形,利用勾股定理列出关于半径r的方程,是解题的关键.
14./102度
【分析】本题主要考查了切线长定理,解题的关键是熟练掌握切线长定理及其推论.令四边形与分别相切于点E、F、G、H,连接,通过证明,即可求解.
【详解】解:令四边形与分别相切于点E、F、G、H,
连接,
∵是的外切四边形,
∴,
∵,
∴,
∴,
同理可得:,
∵,
∴,
∴,
∴,
故答案为:.
15./144度
【分析】本题考查了圆锥的有关计算和弧长公式,根据底面周长等于圆锥的侧面展开图的弧长以及弧长公式求解即可,正确理解圆锥的母线长是圆锥侧面展开图的扇形半径,圆锥的底面圆周长是扇形的弧长是解决本题的关键.
【详解】设圆锥的侧面展开图的圆心角的度数为,根据题意,得
,
,
圆锥的侧面展开图的圆心角的度数为,
故答案为:.
16.
【分析】本题考查了勾股定理和垂径定理,解答此题时要注意进行分类讨论,不要漏解.由于弦与的具体位置不能确定,故应分两种情况进行讨论:①弦与在圆心同侧;②弦与在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
【详解】解:①当弦与在圆心同侧时,如图,
过点O作,垂足为F,交于点E,连接,
∵,
∴,
∵,
∴,
∵,
∴由勾股定理得:,,
∴;
②当弦与在圆心异侧时,如图,
过点O作于点E,反向延长交于点F,连接,
同理,,
,
所以与之间的距离是.
故答案为:.
17.(1)的度数是;
(2)阴影部分的面积是.
【分析】本题考查圆的切线性质,直角三角形性质等知识.
(1)由是半圆O的直径,是半圆O的切线,可得,即得,可得,从而,可得的度数;
(2),可得,,即得,再利用阴影部分的面积等于半圆减去即可解题.
【详解】(1)解:∵是半圆O的直径,
∴,
∵是半圆O的切线,
∴,
∴,
∴;
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
答:的度数是;
(2)解:由(1)知,
∵,
∴,,
∴,
∴阴影部分的面积是-2=2π-2,
答:阴影部分的面积是.
18.(1)见解析
(2)见解析
【分析】(1)根据三角形的内心是三角形的内角平分线的交点得到,,再根据圆周角定理和三角形的外角性质得到,进而利用等腰三角形的等角对等边证得结论;
(2)延长至F,使,证明,和得到,,再根据直角三角形的性质解答即可.
【详解】(1)证明:如图1,连接,
∵点是的内心,
∴,,
∵,
∴,
∴ ,
∴;
(2)解:如图2,延长至F,使,
∵点是的内心,,
∴,,
∵,,
∴,
在和中,
,
∴,
∴,,
过D作于G,则,
在中,,则,
∴,
∵,
∴.
【点睛】本题考查了三角形的内心和外接圆,圆周角定理、全等三角形的判定与性质、三角形的外角性质、直角三角形的性质、等腰三角形的判定与性质、圆内接四边形的两对角互补,熟练掌握相关知识的联系与运用,灵活添加辅助线构造全等三角形求解是解答的关键.
19.(1)见解析
(2)
【分析】对于(1),证明:连接,根据等边对等角,得,可知,即可说明,进而得出答案;
对于(2),连接,根据“两角相等的两个三角形相似”,得,再根据相似三角形的对应边成比例得出答案.
【详解】(1)证明:连接,
∵,
∴.
∵,
∴,
∴,
∴.
∵,
∴.
∵是的半径,
∴是的切线;
(2)解:连接,
∵是直径,
∴.
∵,
∴.
∵,
∴,
∴.
∵,
∴.
∵,
∴,
∴.
【点睛】本题主要考查了等腰三角形的性质,相似三角形的性质和判定,切线的判定等,相似三角形的对应边成比例是求线段长的常用方法.
20.(1)答案见解析
(2)
【分析】(1)根据同弧所对的圆周角相等得到∠ACD=∠DBA,根据 ∠CAB=∠DBA得到∠CAB=∠ACD,进而得到结论;
(2)连结OC,OD,证明所求的阴影部分面积与扇形的面积相等,继而得到结论.
【详解】(1)证明:∵=,
∴∠ACD=∠DBA,
又∠CAB=∠DBA,
∴∠CAB=∠ACD,
∴;
(2)解:如图,连结OC,OD.
∵∠ACD=30°,
∴∠ACD=∠CAB=30°,
∴∠AOD=∠COB=60°,
∴∠COD=180°-∠AOD-∠COB=60°.
∵,
∴S△DOC=S△DBC,
∴S阴影=S弓形COD+S△DOC=S弓形COD+S△DBC=S扇形COD,
∵AB=4,
∴OA=2,
∴S扇形COD=.
∴S阴影=.
【点睛】本题主要考查扇形的面积,同弧所对的圆周角相等,平行线的判定,掌握定理以及公式是解题的关键.
21.(1)△ABC是等边三角形,证明见解析;(2)见解析
【分析】(1)利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;
(2)如图所示,在PC取一点E使得AE=AP,先证明△APE是等边三角形,得到AP=PE,∠AEP=60°,可以推出∠AEC=∠APB,然后证明△APB≌△AEC得到BP=CE,即可证明PC=PE+CE=AP+BP.
【详解】解:(1)△ABC是等边三角形.证明如下:
由圆周角定理:∠BAC=∠CPB,∠ABC=∠APC
∵∠APC=∠CPB=60°,
∴∠BAC=∠ABC=60°,
∴∠ACB=180°-∠BAC-∠ABC=180°-60°-60°=60°.
∴△ABC是等边三角形.
(2)如图所示,在PC取一点E使得AE=AP,
∵∠APE=60°,AP=AE,
∴△APE是等边三角形,
∴AP=PE,∠AEP=60°,
∴∠AEC=120°,
又∵∠APC=∠CPB=60°,
∴∠APB=120°,
∴∠AEC=∠APB,
∵△ABC是等边三角形,
∴AB=AC,
又∵∠ABP=∠ACE,
∴△APB≌△AEC(AAS),
∴BP=CE,
∴PC=PE+CE=AP+BP.
【点睛】本题考查了圆周角定理、等边三角形的性质与判定,全等三角形的性质与判定,解题的关键是掌握圆周角定理,正确求出∠ABC=∠BAC=60°.
22.(1)
(2)
【分析】
(1)连接,则可得;由菱形的性质及等腰三角形的性质得,由此可求得,进而求得结果;
(2)连接,过点B作于F,过点O作于N;由菱形的性质及勾股定理可求得的长;设圆的半径的r,则在中由勾股定理可求得r的值;
由面积相等则可求得,再由勾股定理及等腰三角形的性质即可求得.
【详解】(1)解:如图,连接,
∵是的切线,
∴,
即;
∵四边形是菱形,
∴;
∵,
∴,
∴,
∴,
∴,
∴,
∴;
(2)解:如图,连接,过点B作于F,过点O作于N;
∵四边形是菱形,,
∴,
由勾股定理得;
设圆的半径的r,则,
在中,由勾股定理得:,
解得:,
∴;
∵,
∴;
在中,由勾股定理得:,
∵,
∴.
【点睛】本题考查了圆的切线性质,菱形的性质,勾股定理及等腰三角形的性质,综合运用这些性质与定理是解题的关键.
23.(1)见解析
(2)见解析
(3)见解析
(4)见解析
【分析】(1)作线段的垂直平分线交于点O即可;
(2)连接点A和线段的垂直平分线与的交点D即可;
(3)连接,由垂直平分线的性质可得,由直径所对的圆周角为可知,,则点绕D点顺时针旋转后的对应点为点C,连接并延长交于点H,延长交的延长线于点E,则点E即为点绕D点顺时针旋转后的对应点,连接,即为所求;
(4)证明四边形是矩形,则Q是的中点,由垂径定理得到,由可知为三条高的交点,连接,延长交于点M,则,连接,则即为所求.
【详解】(1)如图所示,点O即为所求,
理由如下:由网格的特点可知,点O和点G分别是所在矩形的对角线交点,也是所在格线的中点,
∴垂直平分,
∴,
∴点O即为所求圆心;
(2)如图所示,即为所求,
理由如下:∵,是直径,
∴,
∴,
即平分交于D点;
(3)如图所示,线段即为所求,
理由如下:∵垂直平分,
∴,
∵是直径,
∴,
∴点绕D点顺时针旋转后的对应点为点C,
连接并延长交于点H,
∴是的直径,
∴,
延长交的延长线于点E,
由(2)可知,,
∴,
∴,
∴点E即为点绕D点顺时针旋转后的对应点,连接,即为所求;
(4)如图所示,即为所求,
理由如下:由(1)可知,点A和点N关于直线轴对称,
∴垂直平分,
∴,
则,
∴四边形是矩形,
∴点Q是的中点,
∴,
∵,
∴点T为三条高的交点,
连接,延长交于点M,
∴,
∴.
【点睛】此题考查了圆周角定理、垂径定理、矩形的判定和性质、垂直平分线的判定和性质、三角形的性质等知识,根据相关定理准确作图是解题的关键.
24.(1)详见解析
(2)
【分析】(1)由垂径定理可得,由此可得,根据同弧或等弧对的圆周角相等可得;
(2)连接,由勾股定理可得,则,设,则,在中,根据勾股定理列方程求出x的值,即可知的长.
本题主要考查了圆的相关性质,垂径定理,同弧或等弧对的圆周角相等以及勾股定理,熟练掌握圆的相关性质是解题的关键.
【详解】(1)证明:是的直径,,
,
又,
,
,
.
(2)解:连接,
,
,
又,,
,
,,
,
由(1)可知,
∴;
设,
,
在中,
,
解得:,
,
.
25.(1)
(2)P(,)
(3)证明见解析
【分析】(1)把A、C坐标代入可得关于a、c的二元一次方程组,解方程组求出a、c的值即可得答案;
(2)如图,设BP与y轴交于点E,直线解析式为,根据(1)中解析式可知D、B两点坐标,可得CD//AB,利用ASA可证明△DCB≌△ECB,可得CE=CD,即可得出点E坐标,利用待定系数法可得直线BP的解析式,联立直线BP与抛物线解析式求出交点坐标即可得答案;
(3)如图,连接MD,MF,设Q(m,-m2+2m+3),F(m,t),根据CD、QF为⊙M的弦可得圆心M是CD、QF的垂直平分线的交点,即可表示出点M坐标,根据MD=MF,利用两点间距离公式可得()2+(2-1)2=(m-1)2+()2,整理可得t=2,即可得答案.
【详解】(1)∵A(﹣1,0)、C(0,3)在抛物线y=ax2+2x+c图象上,
∴,
解得:,
∴抛物线解析式为:.
(2)如图,设BP与y轴交于点E,直线解析式为,
∵点D(m,3)在抛物线上,
∴,
解得:,(与点C重合,舍去),
∴D(2,3),
∴CD//AB,CD=2,
当y=0时,,
解得:,,
∴B(3,0),
∴OB=OC,
∴∠OCB=∠OBC=∠DCB=45°,
在△DCB和△ECB中,
∵,
∴△DCB≌△ECB,
∴CE=CD=2,
∴OE=OC-CE=1,
∴E(0,1),
∴,
解得:,
∴直线BP的解析式为,
联立直线BP与抛物线解析式得:,
解得:(舍去),,
∴P(,).
(3)如图,连接MD,MF,设Q(m,-m2+2m+3),F(m,t),
∵CD、QF为⊙M的弦,
∴圆心M是CD、QF的垂直平分线的交点,
∵C(0,3),D(2,3),QF//y轴,
∴M(1,),
∵MD=MF,
∴2+(2-1)2=(m-1)2+()2,
整理得:t=2,
∴点F在定直线y=2上.
【点睛】本题考查待定系数法求二次函数解析式、全等三角形的判定与性质、二次函数与一次函数的交点问题及圆的性质,综合性强,熟练掌握相关知识及定理是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版九年级数学上册
第二十四章圆单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知的半径为3,点O到直线m的距离为d,若直线m与公共点的个数为2个,则d可取( )
A.0 B.3 C.3.5 D.4
2.已知的半径等于5,圆心到直线的距离为4,那么直线与的公共点的个数是( )
A.0 B.1 C.2 D.无法确定
3.已知如图,点为扇形弧上一动点,,,过点作,,的内心为,设,若点运动时,使得,则点的运动路径长为( )
A. B. C. D.
4.如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为( )
A.π B.π C.π D.π
5.如图,PA,PB是的切线,A、B为切点,若,则的度数为( )
A. B. C. D.
6.某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为,高为,则改建后门洞的圆弧长是( )
A. B. C. D.
7.如图,AB为⊙O的一条弦,C为⊙O上一点,OC∥AB.将劣弧AB沿弦AB翻折,交翻折后的弧AB交AC于点D.若D为翻折后弧AB的中点,则∠ABC=( )
A.110° B.112.5° C.115° D.117.5°
8.如图是一个含有3个正方形的相框,其中∠BCD=∠DEF=90°,AB=2,CD=3,EF=5,将它镶嵌在一个圆形的金属框上,使A,G, H三点刚好在金属框上,则该金属框的半径是( )
A. B. C. D.
9.抛物线与x轴交于A,B两点,D是以为圆心,2为半径的上一动点,E为中点,则线段的长可能为( )
A.1 B.2.5 C.4 D.5
二、填空题
10.如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF= .
11.如图,的两个顶点、在上,的半径为2,,,若动点在上运动,,则的取值范围是 .
12.如图直线与x轴、y轴分别交于点A,B,C是的中点,点D在直线上,以为直径的圆与直线的另一交点为E,交y轴于点F,G,已知,,则的长是 .
13.如图,木工用角尺的短边紧靠⊙于点A,长边与⊙相切于点B,角尺的直角顶点为C,已知,则⊙的半径为 .
14.四边形是的外切四边形,若,则的度数是 .
15.已知一个圆锥底面半径为,母线长为,则这个圆锥的侧面展开图的圆心角度数为 .
16.在半径为2的中,弦,弦,且,则与之间的距离为 .
三、解答题
17.如图,C是圆O被直径分成的半圆上一点,过点C作圆O的切线交AB的延长线于点P,连接.
(1)若,求的度数
(2)在(1)的条件下,若,求图中阴影部分的面积(结果保留和根号).
18.如图,点是的内心,的延长线和的外接圆交于点.
(1)如图1,连接,求证:;
(2)如图2,若,求证:.
19.如图,在等腰中,,以为直径的与交于点D,,垂足为E,的延长线与的延长线交于点F.
(1)求证:是的切线;
(2)若的半径为,,求的长.
20.如图,是以为直径的半圆上的两点,,连结.
(1)求证:.
(2)若,,求阴影部分的面积.
21.如图,A,P,B,C是⊙O上的四点,∠APC=∠CPB=60°.
(1)判断△ABC的形状,并证明你的结论;
(2)求证:PA+PB=PC.
22.菱形的顶点B,C,D在上,O在线段上.
(1)如图1,若是的切线,求的大小;
(2)如图2,若,,与交于点E,求的长.
23.如图,在正方形网格中,每个小正方形的顶点称为格点. B,C为格点,以线段为直径的交纵向格线于A点,连接. 仅用无刻度的直尺在给定网格中按要求作图,画图过程用虚线表示,画图结果用实线表示.
(1)在图1中作出圆心O;
(2)在图1中作平分交于D点:
(3)在图1中作绕D点顺时针旋转后的线段;
(4)在图2的中作弦.
24.如图,是的直径,是的弦,,垂足为,为上一点,且,连接交于点,连接.
(1)求证:;
(2)若,,求的长.
25.抛物线y=ax2+2x+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C(0,3),点D(m,3)在抛物线上.
(1)求抛物线的解析式;
(2)如图1,连接BC、BD,点P在对称轴左侧的抛物线上,若∠PBC=∠DBC,求点P的坐标;
(3)如图2,点Q为第四象限抛物线上一点,经过C、D、Q三点作⊙M,⊙M的弦QF∥y轴,求证:点F在定直线上.
参考答案:
1.A
【分析】本题考查了直线与圆的位置关系,当时,直线与圆相离,当时,直线与圆相切,当时,直线与圆相交,据此即可解答.
【详解】解:∵直线m与公共点的个数为2个,
∴直线m与相交,
∴,
故选:A
2.C
【分析】利用直线与圆的位置关系的判断方法得到直线与相交,然后根据相离的定义对各选项进行判断.
【详解】 的的半径为5,圆心到直线的距离为4,
圆心到直线的距离小于半径,
直线与相交,
直线与有2个公共点.
故选:C.
【点睛】本题考查了直线与圆的位置关系:设的半径为,圆心到直线的距离为,则当直线与相交 ;当直线与相切 ;当直线与相离 ;熟练掌握直线与圆的位置关系是解本题的关键.
3.A
【分析】连接交分别为,连接,证明在线段上运动,根据,得出两个端点,进而根据对称性可得是等腰直角三角形,根据含30度角的直角三角形的性质得出的长,根据直角三角形斜边上的中线等于斜边的一半,求得的长,进而即可求解.
【详解】解:如图,连接交分别为,连接,
∵,,
∴
∵,
∴,,
∴,
∴是等边三角形,
∵的内心为,
∴,
设,
则,,
∵的内心为,
∴
∴
∴
∴,
∴在上运动,
∵,如图,当时,重合,
则
当时,如图,
同理可得,
∴,
根据对称性可得是等腰直角三角形,
过点作于点,如图,
∴在中,,,,
∴在中,.
即点的运动路径长为.
故选:A.
【点睛】本题考查了等边三角形的性质与判定,三角形内心的性质,找到点的运动轨迹是解题的关键.
4.A
【详解】∵AB=5,AC=3,BC=4,∴△ABC为直角三角形.由题意得S△AED=S△ABC,由图形可知S阴影=S△AED+S扇形ADB-S△ABC,∴S阴影=S扇形ADB==π,故选A.
5.B
【分析】根据切线的性质以及四边形的内角和即可求解.
【详解】解:∵PA,PB是的切线,
∴,
,
,
则 ,
故选B.
【点睛】本题考查了切线的性质以及四边形的内角和,掌握切线的性质是解题的关键.
6.C
【分析】利用勾股定理先求得圆弧形的门洞的直径BC,再利用矩形的性质证得是等边三角形,得到,进而求得门洞的圆弧所对的圆心角为,利用弧长公式即可求解.
【详解】如图,连接,,交于点,
∵ ,
∴是直径,
∴,
∵四边形是矩形,
∴,
∵,
∴,
∴是等边三角形,
∴,
∴门洞的圆弧所对的圆心角为 ,
∴改建后门洞的圆弧长是(m),
故选:C
【点睛】本题考查了弧长公式,矩形的性质以及勾股定理的应用,从实际问题转化为数学模型是解题的关键.
7.B
【分析】如图,取 中点,连接,连接,由题意知,且在一条直线上,,,知,根据圆周角定理,等边对等角,三角形内角和定理等可求,,,,,的值,进而求解的值.
【详解】解:如图,取 中点,连接,连接
由题意知,且在一条直线上,,
∴
∴
∵,
∴
∴
∵
∴
∴
∴
∴
故选B.
【点睛】本题考查了垂径定理,圆周角,等边对等角,三角形内角和定理,折叠性质等知识.解题的关键在于对知识的灵活运用.
8.A
【分析】如图,记过A,G, H三点的圆为则是,的垂直平分线的交点, 记的交点为 的交点为 延长交于 为的垂直平分线,结合正方形的性质可得:再设利用勾股定理建立方程,再解方程即可得到答案.
【详解】解:如图,记过A,G, H三点的圆为则是,的垂直平分线的交点,
记的交点为 的交点为 延长交于 为的垂直平分线,结合正方形的性质可得:
四边形为正方形,则
设 而AB=2,CD=3,EF=5,结合正方形的性质可得:
而
又 而
解得:
故选A
【点睛】本题考查的是正方形的性质,三角形外接圆圆心的确定,圆的基本性质,勾股定理的应用,二次根式的化简,确定过A,G, H三点的圆的圆心是解本题的关键.
9.B
【分析】解一元二次方程可得、,即,再利用勾股定理求得,再根据中位线定理可得,进而即可求解.
【详解】解:连接,
设点、,则、是方程的两个根,
解得,,
∴、,
∴,
∵,
∴,
∵E为中点,O为的中点,
∴是的中位线,
∴,
∵,
即,
∴,
∴的长可能为2.5,
故选:B.
【点睛】本题考查解一元二次方程、勾股定理、三角形中位线定理及三角形的三边关系,熟练掌握角形中位线定理及三角形的三边关系是解题的关键.
10.15°
【分析】根据平行四边形的性质和圆的半径相等得到△AOB为等边三角形,根据等腰三角形的三线合一得到∠BOF=∠AOF=30°,根据圆周角定理计算即可.
【详解】解答:
连接OB,
∵四边形ABCO是平行四边形,∴OC=AB,又OA=OB=OC,
∴OA=OB=AB,∴△AOB为等边三角形.
∵OF⊥OC,OC∥AB,∴OF⊥AB,∴∠BOF=∠AOF=30°.
由圆周角定理得 ,
故答案为15°.
11.
【分析】连接,作,且,连接,,,证明得到,再根据勾股定理求得,然后根据两点之间线段最短求解即可.
【详解】解:如图,连接,作,且,连接,,,
∵,
∴,
在和中,
∴,
∴,
在中,,
根据两点之间线段最短得,
∴,
故答案为:.
【点睛】本题主要考查了圆的有关概念、全等三角形的判定与性质、勾股定理、两点之间线段最短、等角的余角相等,添加辅助线构造全等三角形求解是解答的关键.
12.
【分析】如图,设CD的中点为O′,设直线BA交直线y=﹣2于M,直线y=﹣2交y轴于P,作CH⊥OB于H,连接O′F,作AJ⊥DM于J,O′N⊥FG于N.首先利用等腰直角三角形的性质和条件可确定A,B,C的坐标,再设D(m,﹣2),进而可得O′N与O′F的长,而FN=,然后在Rt△O′FN中利用勾股定理构建方程即可求出m,问题即得解决.
【详解】解:如图,设CD的中点为O′,设直线BA交直线y=﹣2于M,直线y=﹣2交y轴于P,作CH⊥OB于H,连接O′F,作AJ⊥DM于J,O′N⊥FG于N.
∵CD是⊙O′的直径,∴∠CED=90°,
∵直线y=﹣x+m(m>0)与x轴、y轴分别交于点A,B,
∴A(m,0),B(0,m),
∴OA=OB,∴∠OAB=45°,
∵OA∥DM,∴∠EMD=∠OAB=45°,
∵∠DEM=90°,∴ED=EM,
∴EC+ED=EC+EM=CM=,
∵JA⊥DM,∴∠AJM=90°,
∴AJ=JM=2,AM=2,
∴BC=CA=4,∴AB=8,∴BO=AO=8,
∴A(8,0),B(0,8),C(4,4),
设D(m,﹣2),则O′((m+4),1),
∴O′N=(m+4),O′F=CD=,
∵O′N⊥FG,∴FN=,
在Rt△O′FN中,由勾股定理,得:,解得m=1,
∴CD=.
故答案为:.
【点睛】本题考查了圆周角定理、等腰直角三角形的判定和性质、勾股定理、垂径定理、一次函数与坐标轴的交点和两点间的距离等知识,解题的关键是添加常用辅助线构造特殊三角形解决问题,具有相当难度,属于中考填空题中的压轴题.
13./
【分析】设圆的半径为rcm,连接OB、OA,过点A作AD⊥OB,垂足为D,利用勾股定理,在Rt△AOD中,得到r2=(r 6)2+82,求出r即可.
【详解】解:连接OB、OA,过点A作AD⊥OB,垂足为D,如图所示:
∵CB与相切于点B,
∴,
∴,
∴四边形ACBD为矩形,
∴,,
设圆的半径为rcm,在Rt△AOD中,根据勾股定理可得:,
即r2=(r 6)2+82,
解得:,
即的半径为.
故答案为:.
【点睛】本题主要考查了切线的性质,矩形的判定和性质,勾股定理,作出辅助线,构造直角三角形,利用勾股定理列出关于半径r的方程,是解题的关键.
14./102度
【分析】本题主要考查了切线长定理,解题的关键是熟练掌握切线长定理及其推论.令四边形与分别相切于点E、F、G、H,连接,通过证明,即可求解.
【详解】解:令四边形与分别相切于点E、F、G、H,
连接,
∵是的外切四边形,
∴,
∵,
∴,
∴,
同理可得:,
∵,
∴,
∴,
∴,
故答案为:.
15./144度
【分析】本题考查了圆锥的有关计算和弧长公式,根据底面周长等于圆锥的侧面展开图的弧长以及弧长公式求解即可,正确理解圆锥的母线长是圆锥侧面展开图的扇形半径,圆锥的底面圆周长是扇形的弧长是解决本题的关键.
【详解】设圆锥的侧面展开图的圆心角的度数为,根据题意,得
,
,
圆锥的侧面展开图的圆心角的度数为,
故答案为:.
16.
【分析】本题考查了勾股定理和垂径定理,解答此题时要注意进行分类讨论,不要漏解.由于弦与的具体位置不能确定,故应分两种情况进行讨论:①弦与在圆心同侧;②弦与在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
【详解】解:①当弦与在圆心同侧时,如图,
过点O作,垂足为F,交于点E,连接,
∵,
∴,
∵,
∴,
∵,
∴由勾股定理得:,,
∴;
②当弦与在圆心异侧时,如图,
过点O作于点E,反向延长交于点F,连接,
同理,,
,
所以与之间的距离是.
故答案为:.
17.(1)的度数是;
(2)阴影部分的面积是.
【分析】本题考查圆的切线性质,直角三角形性质等知识.
(1)由是半圆O的直径,是半圆O的切线,可得,即得,可得,从而,可得的度数;
(2),可得,,即得,再利用阴影部分的面积等于半圆减去即可解题.
【详解】(1)解:∵是半圆O的直径,
∴,
∵是半圆O的切线,
∴,
∴,
∴;
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
答:的度数是;
(2)解:由(1)知,
∵,
∴,,
∴,
∴阴影部分的面积是-2=2π-2,
答:阴影部分的面积是.
18.(1)见解析
(2)见解析
【分析】(1)根据三角形的内心是三角形的内角平分线的交点得到,,再根据圆周角定理和三角形的外角性质得到,进而利用等腰三角形的等角对等边证得结论;
(2)延长至F,使,证明,和得到,,再根据直角三角形的性质解答即可.
【详解】(1)证明:如图1,连接,
∵点是的内心,
∴,,
∵,
∴,
∴ ,
∴;
(2)解:如图2,延长至F,使,
∵点是的内心,,
∴,,
∵,,
∴,
在和中,
,
∴,
∴,,
过D作于G,则,
在中,,则,
∴,
∵,
∴.
【点睛】本题考查了三角形的内心和外接圆,圆周角定理、全等三角形的判定与性质、三角形的外角性质、直角三角形的性质、等腰三角形的判定与性质、圆内接四边形的两对角互补,熟练掌握相关知识的联系与运用,灵活添加辅助线构造全等三角形求解是解答的关键.
19.(1)见解析
(2)
【分析】对于(1),证明:连接,根据等边对等角,得,可知,即可说明,进而得出答案;
对于(2),连接,根据“两角相等的两个三角形相似”,得,再根据相似三角形的对应边成比例得出答案.
【详解】(1)证明:连接,
∵,
∴.
∵,
∴,
∴,
∴.
∵,
∴.
∵是的半径,
∴是的切线;
(2)解:连接,
∵是直径,
∴.
∵,
∴.
∵,
∴,
∴.
∵,
∴.
∵,
∴,
∴.
【点睛】本题主要考查了等腰三角形的性质,相似三角形的性质和判定,切线的判定等,相似三角形的对应边成比例是求线段长的常用方法.
20.(1)答案见解析
(2)
【分析】(1)根据同弧所对的圆周角相等得到∠ACD=∠DBA,根据 ∠CAB=∠DBA得到∠CAB=∠ACD,进而得到结论;
(2)连结OC,OD,证明所求的阴影部分面积与扇形的面积相等,继而得到结论.
【详解】(1)证明:∵=,
∴∠ACD=∠DBA,
又∠CAB=∠DBA,
∴∠CAB=∠ACD,
∴;
(2)解:如图,连结OC,OD.
∵∠ACD=30°,
∴∠ACD=∠CAB=30°,
∴∠AOD=∠COB=60°,
∴∠COD=180°-∠AOD-∠COB=60°.
∵,
∴S△DOC=S△DBC,
∴S阴影=S弓形COD+S△DOC=S弓形COD+S△DBC=S扇形COD,
∵AB=4,
∴OA=2,
∴S扇形COD=.
∴S阴影=.
【点睛】本题主要考查扇形的面积,同弧所对的圆周角相等,平行线的判定,掌握定理以及公式是解题的关键.
21.(1)△ABC是等边三角形,证明见解析;(2)见解析
【分析】(1)利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;
(2)如图所示,在PC取一点E使得AE=AP,先证明△APE是等边三角形,得到AP=PE,∠AEP=60°,可以推出∠AEC=∠APB,然后证明△APB≌△AEC得到BP=CE,即可证明PC=PE+CE=AP+BP.
【详解】解:(1)△ABC是等边三角形.证明如下:
由圆周角定理:∠BAC=∠CPB,∠ABC=∠APC
∵∠APC=∠CPB=60°,
∴∠BAC=∠ABC=60°,
∴∠ACB=180°-∠BAC-∠ABC=180°-60°-60°=60°.
∴△ABC是等边三角形.
(2)如图所示,在PC取一点E使得AE=AP,
∵∠APE=60°,AP=AE,
∴△APE是等边三角形,
∴AP=PE,∠AEP=60°,
∴∠AEC=120°,
又∵∠APC=∠CPB=60°,
∴∠APB=120°,
∴∠AEC=∠APB,
∵△ABC是等边三角形,
∴AB=AC,
又∵∠ABP=∠ACE,
∴△APB≌△AEC(AAS),
∴BP=CE,
∴PC=PE+CE=AP+BP.
【点睛】本题考查了圆周角定理、等边三角形的性质与判定,全等三角形的性质与判定,解题的关键是掌握圆周角定理,正确求出∠ABC=∠BAC=60°.
22.(1)
(2)
【分析】
(1)连接,则可得;由菱形的性质及等腰三角形的性质得,由此可求得,进而求得结果;
(2)连接,过点B作于F,过点O作于N;由菱形的性质及勾股定理可求得的长;设圆的半径的r,则在中由勾股定理可求得r的值;
由面积相等则可求得,再由勾股定理及等腰三角形的性质即可求得.
【详解】(1)解:如图,连接,
∵是的切线,
∴,
即;
∵四边形是菱形,
∴;
∵,
∴,
∴,
∴,
∴,
∴,
∴;
(2)解:如图,连接,过点B作于F,过点O作于N;
∵四边形是菱形,,
∴,
由勾股定理得;
设圆的半径的r,则,
在中,由勾股定理得:,
解得:,
∴;
∵,
∴;
在中,由勾股定理得:,
∵,
∴.
【点睛】本题考查了圆的切线性质,菱形的性质,勾股定理及等腰三角形的性质,综合运用这些性质与定理是解题的关键.
23.(1)见解析
(2)见解析
(3)见解析
(4)见解析
【分析】(1)作线段的垂直平分线交于点O即可;
(2)连接点A和线段的垂直平分线与的交点D即可;
(3)连接,由垂直平分线的性质可得,由直径所对的圆周角为可知,,则点绕D点顺时针旋转后的对应点为点C,连接并延长交于点H,延长交的延长线于点E,则点E即为点绕D点顺时针旋转后的对应点,连接,即为所求;
(4)证明四边形是矩形,则Q是的中点,由垂径定理得到,由可知为三条高的交点,连接,延长交于点M,则,连接,则即为所求.
【详解】(1)如图所示,点O即为所求,
理由如下:由网格的特点可知,点O和点G分别是所在矩形的对角线交点,也是所在格线的中点,
∴垂直平分,
∴,
∴点O即为所求圆心;
(2)如图所示,即为所求,
理由如下:∵,是直径,
∴,
∴,
即平分交于D点;
(3)如图所示,线段即为所求,
理由如下:∵垂直平分,
∴,
∵是直径,
∴,
∴点绕D点顺时针旋转后的对应点为点C,
连接并延长交于点H,
∴是的直径,
∴,
延长交的延长线于点E,
由(2)可知,,
∴,
∴,
∴点E即为点绕D点顺时针旋转后的对应点,连接,即为所求;
(4)如图所示,即为所求,
理由如下:由(1)可知,点A和点N关于直线轴对称,
∴垂直平分,
∴,
则,
∴四边形是矩形,
∴点Q是的中点,
∴,
∵,
∴点T为三条高的交点,
连接,延长交于点M,
∴,
∴.
【点睛】此题考查了圆周角定理、垂径定理、矩形的判定和性质、垂直平分线的判定和性质、三角形的性质等知识,根据相关定理准确作图是解题的关键.
24.(1)详见解析
(2)
【分析】(1)由垂径定理可得,由此可得,根据同弧或等弧对的圆周角相等可得;
(2)连接,由勾股定理可得,则,设,则,在中,根据勾股定理列方程求出x的值,即可知的长.
本题主要考查了圆的相关性质,垂径定理,同弧或等弧对的圆周角相等以及勾股定理,熟练掌握圆的相关性质是解题的关键.
【详解】(1)证明:是的直径,,
,
又,
,
,
.
(2)解:连接,
,
,
又,,
,
,,
,
由(1)可知,
∴;
设,
,
在中,
,
解得:,
,
.
25.(1)
(2)P(,)
(3)证明见解析
【分析】(1)把A、C坐标代入可得关于a、c的二元一次方程组,解方程组求出a、c的值即可得答案;
(2)如图,设BP与y轴交于点E,直线解析式为,根据(1)中解析式可知D、B两点坐标,可得CD//AB,利用ASA可证明△DCB≌△ECB,可得CE=CD,即可得出点E坐标,利用待定系数法可得直线BP的解析式,联立直线BP与抛物线解析式求出交点坐标即可得答案;
(3)如图,连接MD,MF,设Q(m,-m2+2m+3),F(m,t),根据CD、QF为⊙M的弦可得圆心M是CD、QF的垂直平分线的交点,即可表示出点M坐标,根据MD=MF,利用两点间距离公式可得()2+(2-1)2=(m-1)2+()2,整理可得t=2,即可得答案.
【详解】(1)∵A(﹣1,0)、C(0,3)在抛物线y=ax2+2x+c图象上,
∴,
解得:,
∴抛物线解析式为:.
(2)如图,设BP与y轴交于点E,直线解析式为,
∵点D(m,3)在抛物线上,
∴,
解得:,(与点C重合,舍去),
∴D(2,3),
∴CD//AB,CD=2,
当y=0时,,
解得:,,
∴B(3,0),
∴OB=OC,
∴∠OCB=∠OBC=∠DCB=45°,
在△DCB和△ECB中,
∵,
∴△DCB≌△ECB,
∴CE=CD=2,
∴OE=OC-CE=1,
∴E(0,1),
∴,
解得:,
∴直线BP的解析式为,
联立直线BP与抛物线解析式得:,
解得:(舍去),,
∴P(,).
(3)如图,连接MD,MF,设Q(m,-m2+2m+3),F(m,t),
∵CD、QF为⊙M的弦,
∴圆心M是CD、QF的垂直平分线的交点,
∵C(0,3),D(2,3),QF//y轴,
∴M(1,),
∵MD=MF,
∴2+(2-1)2=(m-1)2+()2,
整理得:t=2,
∴点F在定直线y=2上.
【点睛】本题考查待定系数法求二次函数解析式、全等三角形的判定与性质、二次函数与一次函数的交点问题及圆的性质,综合性强,熟练掌握相关知识及定理是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
