2024-2025学年度五年级上册第六单元三角形面积测试卷(含解析)
文档属性
| 名称 | 2024-2025学年度五年级上册第六单元三角形面积测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 216.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-28 00:00:00 | ||
图片预览




文档简介
/ 让教学更有效 精品 |
2024-2025学年度五年级上册第六单元 三角形面积测试卷
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
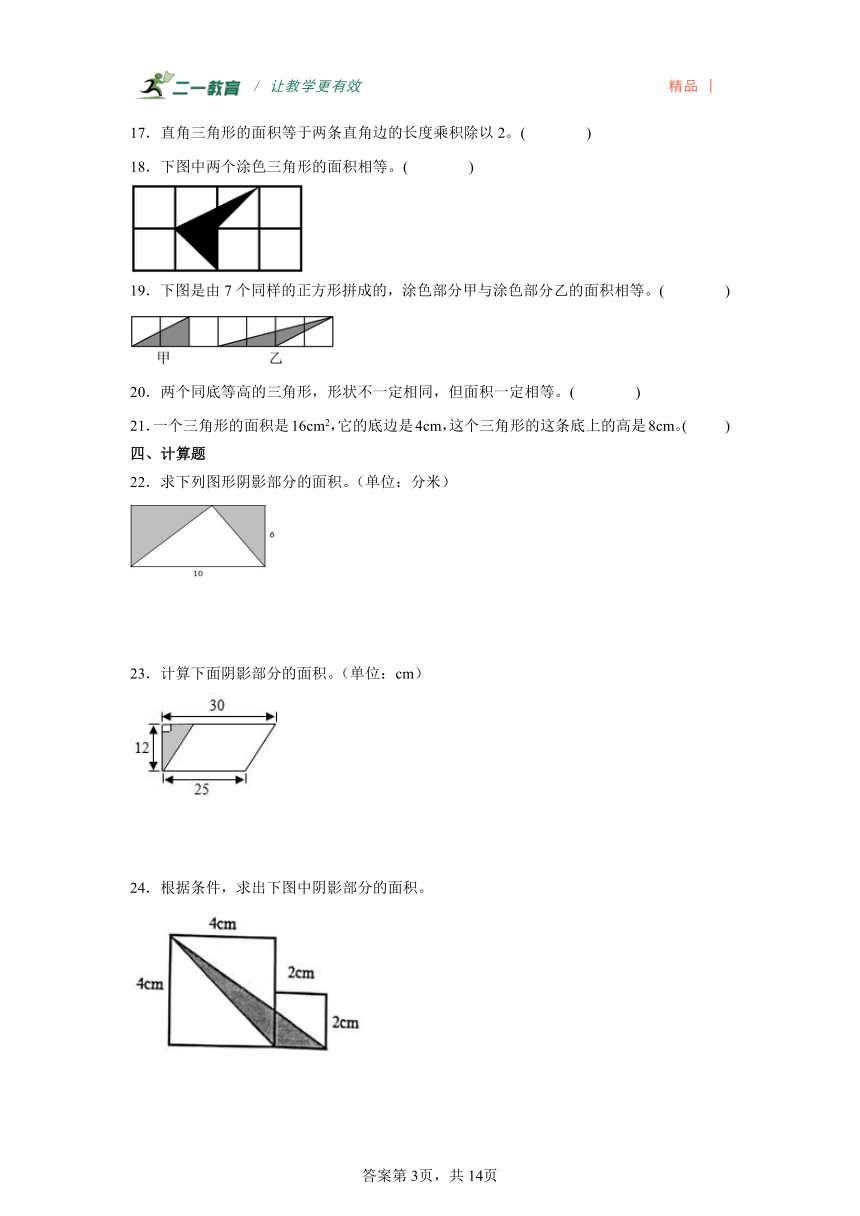
得分
一、选择题
1.一个三角形的面积是40cm2,高是5cm,它的底是( )cm。
A.4 B.8 C.16
2.芳芳要围一个底边是30厘米,面积是90平方厘米的等边三角形铁架,那么这个铁架的高是( )厘米。
A.6 B.9 C.5
3.一个三角形和一个平行四边形等底等高,这个平行四边形的面积比这个三角形的面积大2.6m2,这个平行四边形的面积是( )m2。
A.7.8 B.3.9 C.5.2
4.如图,两条平行线之间的两个图形的面积相比较,( )面积大。
A.平行四边形 B.三角形 C.一样大
5.李大爷家有一个长方形院子(如下图),几个小朋友在院子里踢足球,随意踢一下足球。下面说法正确的是( )。
A.足球落在空白部分的可能性大B.足球落在阴影部分的可能性大
C.足球一定会落在阴影部分 D.足球落在阴影部分、空白部分的可能性一样大
6.下面是三个完全相同的长方形,它们涂色部分的面积相比,( )。
A.图①最大 B.图②最大 C.图③最大 D.一样大
7.如图是由8个正方形拼成的,甲、乙、丙三个三角形的面积相比( )。
A.甲>乙>丙 B.甲=乙=丙 C.甲<乙<丙
二、填空题
8.把一个平行四边形分成三个三角形(如图所示)。如果①部分面积与③部分面积的和是12cm2,则平行四边形的面积是( )cm2。
9.一个直角三角形的三条边分别是6cm、8cm、10cm,这个直角三角形的面积是( )cm2,斜边为底时,高是( )cm。
10.“文明驾车减减速,优雅风度让让人。”这是某地减速慢行的宣传语。下面是一块警示牌,它的面积是( )dm2。
11.如图,三角形的面积是,则平行四边形的面积是( )。
12.一个三角形和一个平行四边形等底等高,已知平行四边形与三角形的面积之和是3.9dm2,平行四边形的面积是( )dm2,三角形的面积是( )dm2。
13.一个三角形与一个平行四边形的面积相等,底也相等,三角形的高是4分米,平行四边形的高是( )分米。
14.一个直角三角形的三条边分别是5cm、12cm、13cm,这个三角形的面积是( )cm2,斜边上的高是( )cm。(“四舍五入”精确到个位)
15.一个等腰三角形的底是10米,腰是a米,底边上的高是8米,这个三角形的周长是( )米,面积是( )平方米。
16.红领巾是少先队员的标志,它有两种规格,其中小号红领巾的底是100cm,该底边上的高约33cm,小号红领巾的面积约是( )cm2。
三、判断题
17.直角三角形的面积等于两条直角边的长度乘积除以2。( )
18.下图中两个涂色三角形的面积相等。( )
19.下图是由7个同样的正方形拼成的,涂色部分甲与涂色部分乙的面积相等。( )
20.两个同底等高的三角形,形状不一定相同,但面积一定相等。( )
21.一个三角形的面积是16cm2,它的底边是4cm,这个三角形的这条底上的高是8cm。( )
四、计算题
22.求下列图形阴影部分的面积。(单位:分米)
23.计算下面阴影部分的面积。(单位:cm)
24.根据条件,求出下图中阴影部分的面积。
五、解答题
25.正方形ABCD的边长是6厘米,已知DE是EC长度的2倍,求CF的长。
26.一块三角形地,底是500米,高是1440米,这块地的面积是多少?如果用拖拉机每天耕18公顷,这块地几天才能耕完?
27.阳光小学有一块三角形的宣传栏,底2米,高3米.在宣传栏的两面刷油漆共用1200克,平均每平方米刷油漆多少克?
28.如图所示,已知四边形ABCD中,E、F分别是AD、BC的中点,连接DF、BE。四边形ABCD的面积为10,则四边形EDFB的面积是多少?
29.如图,三角形ABC,D是BC的中点,E,F是AC的三等分点。已知三角形ABF的面积是108平方分米,那么三角形CDE的面积是多少平方分米?
参考答案:
1.C
【分析】根据三角形的面积=底×高÷2可得,三角形的底=三角形的面积×2÷高,据此代入数据解答即可。
【详解】40×2÷5
=80÷5
=16(cm)
它的底是16cm。
故答案为:C
2.A
【分析】由三角形的面积=底×高÷2,可得三角形的高=面积×2÷底,代入数据计算即可。
【详解】
(厘米)
即这个铁架的高是6厘米;
故答案为:A
3.C
【分析】根据等底等高的平行四边形的面积是三角形的面积的2倍,把三角形的面积看成1份,则平行四边形的面积是2份,则相差(2-1)份,由此可得,平行四边形的面积比三角形大的面积就是三角形的面积,进而列式为:2.6×2,计算即可求出平行四边形的面积。
【详解】2-1=1(份)
2.6×2=5.2(m2)
这个平行四边形的面积是5.2m2。
故答案为:C
4.C
【分析】通过图可知,两个图形的高都是两条平行线之间的距离,所以它们的高相等,可以假设高是10cm,则根据平行四边形的面积公式:底×高;三角形的面积公式:底×高÷2,把数代入求出两个图形的面积,然后比较即可。
【详解】假设高是10cm;
三角形的面积:10×10÷2
=100÷2
=50(cm2)
平行四边形的面积:5×10=50(cm2)
平行四边形的面积=三角形的面积
故答案为:C
5.D
【分析】长方形面积=长×宽,三角形面积=底×高÷2,图中空白部分的面积=长方形面积-阴影部分面积。据此,将空白部分和阴影部分的面积分别表示出来,再对比大小,哪块面积大,足球停在这个区域的可能性就大。如果面积一样大,那么停在两个区域的可能性就一样大。
【详解】设长为a,宽为b,则三角形面积为:ab÷2,即阴影部分的面积为:ab÷2。
长方形面积为:ab;
空白面积:ab-ab÷2=ab÷2;
ab÷2=ab÷2,所以,空白部分和阴影部分的面积相等,那么足球落在阴影部分、空白部分的可能性一样大。
说法正确的是足球落在阴影部分、空白部分的可能性一样大。
故答案为:D
6.D
【分析】可以假设该长方形长为4厘米,宽为2厘米;观察图①涂色部分是个三角形,它的底和长方形的长相等,它的高和长方形的宽相等;观察图②涂色部分是两个大小相同的三角形,它们的底和长方形的长相等,它们的高等于长方形的宽的一半;观察图③涂色部分是两个大小相同的三角形,它们的底等于长方形的长的一半,它们的高和长方形的宽相等。根据三角形的面积=底×高÷2,算出每个长方形的涂色部分的面积,再进行大小比较即可。
【详解】假设该长方形长为4厘米,宽为2厘米。
图①涂色部分面积:
4×2÷2=4(平方厘米)
图②涂色部分面积:
2÷2=1(厘米)
4×1÷2×2=4(平方厘米)
图③涂色部分面积:
4÷2=2(厘米)
2×2÷2×2=4(平方厘米)
4=4=4,因此它们涂色部分的面积一样大。
故答案为:D
7.B
【分析】观察图形可知,甲、乙、丙三个三角形的底和高都是正方形的边长,根据三角形的面积公式:S=ab÷2,等底等高的三角形的面积相等,据此选择即可。
【详解】因为甲、乙、丙三个三角形等底等高,所以它们三个三角形的面积都相等,即甲=乙=丙。
故答案为:B
【点睛】本题考查三角形的面积,明确等底等高的三角形的面积相等是解题的关键。
8.24
【分析】因为等底等高的平行四边形的面积是三角形面积的2倍,通过观察图形可知,三角形①的面积+三角形③的面积=三角形②的面积,所以这个平行四边形的面积是三角形②的面积的2倍,据此解答。
【详解】12×2=24(cm2)
平行四边形的面积是24cm2。
【点睛】此题考查的目的是理解掌握等底等高的平行四边形和三角形面积之间的关系及应用。
9. 24 4.8
【分析】直角三角形中最长的边是斜边,其两条直角边互为彼此的底和高,利用三角形面积公式:三角形面积=底×高÷2,将数据代入即可求出该直角三角形的面积;
再根据三角形的高=三角形面积×2÷底,据此代入数据可以求出该直角三角形斜边上的高为多少。
【详解】由分析可得:
6×8÷2
=48÷2
=24(cm2)
24×2÷10
=48÷10
=4.8(cm)
综上所述:一个直角三角形的三条边分别是6cm、8cm、10cm,这个直角三角形的面积是24cm2,斜边为底时,高是4.8cm。
10.15.6
【分析】从图中可知,警示牌是一个底为6dm、高为5.2dm的三角形,根据三角形的面积=底×高÷2,代入数据计算即可求出它的面积。
【详解】6×5.2÷2
=31.2÷2
=15.6(dm2)
它的面积是15.6dm2。
11.11.2dm2/11.2平方分米
【分析】三角形和平行四边形等底等高,等底等高的平行四边形和三角形,平行四边形面积是三角形面积的2倍,直接用三角形面积×2=平行四边形面积,据此分析。
【详解】5.6×2=11.2(dm2)
平行四边形的面积是11.2dm2。
【点睛】关键是掌握并灵活运用平行四边形和三角形面积公式。
12. 2.6 1.3
【分析】根据“平行四边形面积=底×高、三角形面积=底×高÷2”可知,三角形和平行四边形等底等高时,平行四边形的面积是三角形面积的2倍,可以看作三角形的面积是1份,平行四边形的面积是2份;已知它们的面积和是3.9dm2,除以总份数(2+1)份,求出一份数,即三角形的面积,再乘2,就是平行四边形的面积。
【详解】三角形的面积:
3.9÷(2+1)
=3.9÷3
=1.3(dm2)
平行四边形的面积:1.3×2=2.6(dm2)
所以,平行四边形的面积是2.6dm2,三角形的面积是1.3dm2。
【点睛】掌握等底等高的平行四边形与三角形的面积之间的关系是解题的关键。
13.2
【分析】三角形面积公式:面积=底×高÷2,平行四边形面积公式:面积=底×高;根据题意可知,三角形面积=平行四边形面积;三角形的底=平行四边形的底,即三角形的底×三角形的高÷2=平行四边形底×平行四边形高;由此可知,三角形的高÷2=平行四边形的高;由此求出平行四边形的高。
【详解】4÷2=2(分米)
一个三角形与一个平行四边形的面积相等,底也相等,三角形的高是4分米,平行四边形的高是2分米。
14. 30 5
【分析】直角三角形中斜边最长,两条直角边互为彼此的底和高,利用“三角形的面积=底×高÷2”求出这个三角形的面积,最后根据“高=三角形的面积×2÷底”求出斜边上的高,据此解答。
【详解】分析可知,这个直角三角形的两条直角边分别是5cm和12cm,斜边是13cm。
5×12÷2
=60÷2
=30(cm2)
30×2÷13
=60÷13
≈5(cm)
所以,这个三角形的面积是30cm2,斜边上的高是5cm。
【点睛】掌握三角形的面积计算公式是解答题目的关键。
15. 10+2a 40
【分析】等腰三角形的周长=底长+腰长×2,三角形的面积=底×高÷2;据此将数据代入即可解答。
【详解】三角形的周长:10+2a(米)
三角形的面积:
10×8÷2
=80÷2
=40(平方米)
即这个三角形的周长是(10+2a)米,面积是40平方米。
16.1650
【分析】根据三角形的面积=底×高÷2,代入数据解答即可。
【详解】100×33÷2
=3300÷2
=1650(cm2)
所以小号红领巾的面积约是1650。
17.√
【分析】三角形面积公式:面积=底×高÷2,在直角三角形中,由于两条直角边是互相垂直的,所以一条直角边看作底,另一条直角边看作高,直角三角形面积等于两条直角边的长度乘积除以2,据此解答。
【详解】根据分析可知,直角三角形的面积等于两条直角边的长度乘积除以2。
原题干说法正确。
故答案为:√
18.√
【分析】图中每个正方形大小相等,可以设正方形的边长是1厘米,然后根据三角形的面积=底×高÷2,分别求出两个涂色三角形的面积,再比较,得出结论。
【详解】设正方形的边长是1厘米。
上面涂色三角形的面积:1×1÷2=0.5(平方厘米)
下面涂色三角形的面积:1×1÷2=0.5(平方厘米)
0.5=0.5
所以,两个涂色三角形的面积相等。
原题说法正确。
故答案为:√
19.√
【分析】等底等高的三角形面积相等。同样的正方形,则每个正方形的边长相等。甲三角形的底是2个正方形的边长,高是1个正方形的边长。乙三角形是底也是2个正方形的边长,高是1个正方形的边长。三角形的面积=底×高÷2。
【详解】设正方形的边长为1。
甲面积:2×1÷2=1
乙面积:2×1÷2=1
1=1
故答案为:√
20.√
【分析】三角形面积=底×高÷2,等底等高的两个三角形,形状不一定相同,面积相等,据此分析。
【详解】
如图,两个同底等高的三角形,形状不同,面积相等,所以原题说法正确。
故答案为:√
21.√
【分析】根据三角形面积公式:面积=底×高÷2,高=面积×2÷底,代入数据,求出高,再进行比较,即可解答。
【详解】16×2÷4
=32÷4
=8(cm)
一个三角形的面积是16cm2,它的底边是4cm,这个三角形的这条底上的高是8cm。
原题干说法正确。
故答案为:√
22.30平方分米
【分析】观察图形可知,空白三角形的底相当于长方形的长,高相当于长方形的宽,阴影部分的面积=长方形的面积-三角形的面积,根据长方形的面积公式:S=ab,三角形的面积公式:S=ah÷2,据此计算即可。
【详解】10×6-10×6÷2
=60-30
=30(平方分米)
23.30cm2
【分析】观察图形可知,阴影部分是一个底是(30-25)cm,高是12cm的三角形,根据三角形的面积=底×高÷2,代入数据计算即可。
【详解】(30-25)×12÷2
=5×12÷2
=60÷2
=30(cm2)
阴影部分的面积是30cm2。
24.4平方厘米
【分析】从图中可以看出,阴影部分是一个三角形,底是小正方形的边长,高是大正方形的边长,根据“三角形面积=底×高÷2”即可求出阴影部分的面积。
【详解】2×4÷2
=8÷2
=4(平方厘米)
所以,阴影部分的面积是4平方厘米。
25.3厘米
【分析】正方形ABCD的边长是6厘米,已知DE是EC长度的2倍,根据和倍问题公式:“和÷(倍数+1)=较小数,较小数×倍数=较大数”求出DE的长,再用三角形ADF的面积减去三角形ADE的面积,求出三角形DEF的面积,三角形ADF的底是6厘米、高是6厘米,三角形ADE的底是6厘米、高是4厘米,根据三角形的面积=底×高÷2,代入数据分别求出三角形ADF的面积和三角形ADE的面积,再相减求出三角形DEF的面积,CF边是三角形DEF以DE边为底的高,求CF,用三角形DEF面积的2倍除以DE即可解答。
【详解】6×6÷2
=36÷2
=18(平方厘米)
6÷(2+1)×2
=6÷3×2
=2×2
=4(厘米)
6×4÷2
=24÷2
=12(平方厘米)
18-12=6(平方厘米)
6×2÷4
=12÷4
=3(厘米)
答:CF的边长是3厘米。
26.2天
【分析】根据三角形的面积=底×高÷2,代入数据求出三角形菜地的面积是多少平方米,再根据1公顷=10000平方米,把平方米化成公顷,再根据除法的意义,用三角形的面积除以拖拉机每天耕地的公顷数即可解答。
【详解】500×1440÷2
=720000÷2
=360000(平方米)
360000平方米=36公顷
36÷18=2(天)
答:这块地2天才能耕完。
27.200克
【详解】1200÷(2×3÷2×2)=200(克)
28.5
【分析】如图,连接BD
△BED是△ABD面积的一半,△BDF是△BDC面积的一半,那么,可推出,据此解答即可。
【详解】10÷2=5
答:四边形EDFB的面积是5。
29.54平方分米
【分析】E,F是AC的三等分点,所以AF=EF=EC。因为EF+EC = FC ,所以2AF=FC。三角形BCF和三角形ABF的高相等,且2AF=FC,所以三角形BCF的面积是三角形ABF的2倍,三角形ABF的面积是108平方分米,用乘法计算,求出三角形BCF的面积;D是BC的中点,所以三角形FDC的面积是三角形BCF的面积的一半,用除法计算,求出三角形FDC的面积;又因为EF=EC,所以三角形CDE的面积是三角形FDC的面积的一半,用除法计算,求出三角形CDE的面积,据此解答。
【详解】108×2=216(平方分米)
216÷2=108(平方分米)
108÷2=54(平方分米)
答:三角形CDE的面积是54平方分米。
答案第1页,共2页
答案第1页,共2页
2024-2025学年度五年级上册第六单元 三角形面积测试卷
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
一、选择题
1.一个三角形的面积是40cm2,高是5cm,它的底是( )cm。
A.4 B.8 C.16
2.芳芳要围一个底边是30厘米,面积是90平方厘米的等边三角形铁架,那么这个铁架的高是( )厘米。
A.6 B.9 C.5
3.一个三角形和一个平行四边形等底等高,这个平行四边形的面积比这个三角形的面积大2.6m2,这个平行四边形的面积是( )m2。
A.7.8 B.3.9 C.5.2
4.如图,两条平行线之间的两个图形的面积相比较,( )面积大。
A.平行四边形 B.三角形 C.一样大
5.李大爷家有一个长方形院子(如下图),几个小朋友在院子里踢足球,随意踢一下足球。下面说法正确的是( )。
A.足球落在空白部分的可能性大B.足球落在阴影部分的可能性大
C.足球一定会落在阴影部分 D.足球落在阴影部分、空白部分的可能性一样大
6.下面是三个完全相同的长方形,它们涂色部分的面积相比,( )。
A.图①最大 B.图②最大 C.图③最大 D.一样大
7.如图是由8个正方形拼成的,甲、乙、丙三个三角形的面积相比( )。
A.甲>乙>丙 B.甲=乙=丙 C.甲<乙<丙
二、填空题
8.把一个平行四边形分成三个三角形(如图所示)。如果①部分面积与③部分面积的和是12cm2,则平行四边形的面积是( )cm2。
9.一个直角三角形的三条边分别是6cm、8cm、10cm,这个直角三角形的面积是( )cm2,斜边为底时,高是( )cm。
10.“文明驾车减减速,优雅风度让让人。”这是某地减速慢行的宣传语。下面是一块警示牌,它的面积是( )dm2。
11.如图,三角形的面积是,则平行四边形的面积是( )。
12.一个三角形和一个平行四边形等底等高,已知平行四边形与三角形的面积之和是3.9dm2,平行四边形的面积是( )dm2,三角形的面积是( )dm2。
13.一个三角形与一个平行四边形的面积相等,底也相等,三角形的高是4分米,平行四边形的高是( )分米。
14.一个直角三角形的三条边分别是5cm、12cm、13cm,这个三角形的面积是( )cm2,斜边上的高是( )cm。(“四舍五入”精确到个位)
15.一个等腰三角形的底是10米,腰是a米,底边上的高是8米,这个三角形的周长是( )米,面积是( )平方米。
16.红领巾是少先队员的标志,它有两种规格,其中小号红领巾的底是100cm,该底边上的高约33cm,小号红领巾的面积约是( )cm2。
三、判断题
17.直角三角形的面积等于两条直角边的长度乘积除以2。( )
18.下图中两个涂色三角形的面积相等。( )
19.下图是由7个同样的正方形拼成的,涂色部分甲与涂色部分乙的面积相等。( )
20.两个同底等高的三角形,形状不一定相同,但面积一定相等。( )
21.一个三角形的面积是16cm2,它的底边是4cm,这个三角形的这条底上的高是8cm。( )
四、计算题
22.求下列图形阴影部分的面积。(单位:分米)
23.计算下面阴影部分的面积。(单位:cm)
24.根据条件,求出下图中阴影部分的面积。
五、解答题
25.正方形ABCD的边长是6厘米,已知DE是EC长度的2倍,求CF的长。
26.一块三角形地,底是500米,高是1440米,这块地的面积是多少?如果用拖拉机每天耕18公顷,这块地几天才能耕完?
27.阳光小学有一块三角形的宣传栏,底2米,高3米.在宣传栏的两面刷油漆共用1200克,平均每平方米刷油漆多少克?
28.如图所示,已知四边形ABCD中,E、F分别是AD、BC的中点,连接DF、BE。四边形ABCD的面积为10,则四边形EDFB的面积是多少?
29.如图,三角形ABC,D是BC的中点,E,F是AC的三等分点。已知三角形ABF的面积是108平方分米,那么三角形CDE的面积是多少平方分米?
参考答案:
1.C
【分析】根据三角形的面积=底×高÷2可得,三角形的底=三角形的面积×2÷高,据此代入数据解答即可。
【详解】40×2÷5
=80÷5
=16(cm)
它的底是16cm。
故答案为:C
2.A
【分析】由三角形的面积=底×高÷2,可得三角形的高=面积×2÷底,代入数据计算即可。
【详解】
(厘米)
即这个铁架的高是6厘米;
故答案为:A
3.C
【分析】根据等底等高的平行四边形的面积是三角形的面积的2倍,把三角形的面积看成1份,则平行四边形的面积是2份,则相差(2-1)份,由此可得,平行四边形的面积比三角形大的面积就是三角形的面积,进而列式为:2.6×2,计算即可求出平行四边形的面积。
【详解】2-1=1(份)
2.6×2=5.2(m2)
这个平行四边形的面积是5.2m2。
故答案为:C
4.C
【分析】通过图可知,两个图形的高都是两条平行线之间的距离,所以它们的高相等,可以假设高是10cm,则根据平行四边形的面积公式:底×高;三角形的面积公式:底×高÷2,把数代入求出两个图形的面积,然后比较即可。
【详解】假设高是10cm;
三角形的面积:10×10÷2
=100÷2
=50(cm2)
平行四边形的面积:5×10=50(cm2)
平行四边形的面积=三角形的面积
故答案为:C
5.D
【分析】长方形面积=长×宽,三角形面积=底×高÷2,图中空白部分的面积=长方形面积-阴影部分面积。据此,将空白部分和阴影部分的面积分别表示出来,再对比大小,哪块面积大,足球停在这个区域的可能性就大。如果面积一样大,那么停在两个区域的可能性就一样大。
【详解】设长为a,宽为b,则三角形面积为:ab÷2,即阴影部分的面积为:ab÷2。
长方形面积为:ab;
空白面积:ab-ab÷2=ab÷2;
ab÷2=ab÷2,所以,空白部分和阴影部分的面积相等,那么足球落在阴影部分、空白部分的可能性一样大。
说法正确的是足球落在阴影部分、空白部分的可能性一样大。
故答案为:D
6.D
【分析】可以假设该长方形长为4厘米,宽为2厘米;观察图①涂色部分是个三角形,它的底和长方形的长相等,它的高和长方形的宽相等;观察图②涂色部分是两个大小相同的三角形,它们的底和长方形的长相等,它们的高等于长方形的宽的一半;观察图③涂色部分是两个大小相同的三角形,它们的底等于长方形的长的一半,它们的高和长方形的宽相等。根据三角形的面积=底×高÷2,算出每个长方形的涂色部分的面积,再进行大小比较即可。
【详解】假设该长方形长为4厘米,宽为2厘米。
图①涂色部分面积:
4×2÷2=4(平方厘米)
图②涂色部分面积:
2÷2=1(厘米)
4×1÷2×2=4(平方厘米)
图③涂色部分面积:
4÷2=2(厘米)
2×2÷2×2=4(平方厘米)
4=4=4,因此它们涂色部分的面积一样大。
故答案为:D
7.B
【分析】观察图形可知,甲、乙、丙三个三角形的底和高都是正方形的边长,根据三角形的面积公式:S=ab÷2,等底等高的三角形的面积相等,据此选择即可。
【详解】因为甲、乙、丙三个三角形等底等高,所以它们三个三角形的面积都相等,即甲=乙=丙。
故答案为:B
【点睛】本题考查三角形的面积,明确等底等高的三角形的面积相等是解题的关键。
8.24
【分析】因为等底等高的平行四边形的面积是三角形面积的2倍,通过观察图形可知,三角形①的面积+三角形③的面积=三角形②的面积,所以这个平行四边形的面积是三角形②的面积的2倍,据此解答。
【详解】12×2=24(cm2)
平行四边形的面积是24cm2。
【点睛】此题考查的目的是理解掌握等底等高的平行四边形和三角形面积之间的关系及应用。
9. 24 4.8
【分析】直角三角形中最长的边是斜边,其两条直角边互为彼此的底和高,利用三角形面积公式:三角形面积=底×高÷2,将数据代入即可求出该直角三角形的面积;
再根据三角形的高=三角形面积×2÷底,据此代入数据可以求出该直角三角形斜边上的高为多少。
【详解】由分析可得:
6×8÷2
=48÷2
=24(cm2)
24×2÷10
=48÷10
=4.8(cm)
综上所述:一个直角三角形的三条边分别是6cm、8cm、10cm,这个直角三角形的面积是24cm2,斜边为底时,高是4.8cm。
10.15.6
【分析】从图中可知,警示牌是一个底为6dm、高为5.2dm的三角形,根据三角形的面积=底×高÷2,代入数据计算即可求出它的面积。
【详解】6×5.2÷2
=31.2÷2
=15.6(dm2)
它的面积是15.6dm2。
11.11.2dm2/11.2平方分米
【分析】三角形和平行四边形等底等高,等底等高的平行四边形和三角形,平行四边形面积是三角形面积的2倍,直接用三角形面积×2=平行四边形面积,据此分析。
【详解】5.6×2=11.2(dm2)
平行四边形的面积是11.2dm2。
【点睛】关键是掌握并灵活运用平行四边形和三角形面积公式。
12. 2.6 1.3
【分析】根据“平行四边形面积=底×高、三角形面积=底×高÷2”可知,三角形和平行四边形等底等高时,平行四边形的面积是三角形面积的2倍,可以看作三角形的面积是1份,平行四边形的面积是2份;已知它们的面积和是3.9dm2,除以总份数(2+1)份,求出一份数,即三角形的面积,再乘2,就是平行四边形的面积。
【详解】三角形的面积:
3.9÷(2+1)
=3.9÷3
=1.3(dm2)
平行四边形的面积:1.3×2=2.6(dm2)
所以,平行四边形的面积是2.6dm2,三角形的面积是1.3dm2。
【点睛】掌握等底等高的平行四边形与三角形的面积之间的关系是解题的关键。
13.2
【分析】三角形面积公式:面积=底×高÷2,平行四边形面积公式:面积=底×高;根据题意可知,三角形面积=平行四边形面积;三角形的底=平行四边形的底,即三角形的底×三角形的高÷2=平行四边形底×平行四边形高;由此可知,三角形的高÷2=平行四边形的高;由此求出平行四边形的高。
【详解】4÷2=2(分米)
一个三角形与一个平行四边形的面积相等,底也相等,三角形的高是4分米,平行四边形的高是2分米。
14. 30 5
【分析】直角三角形中斜边最长,两条直角边互为彼此的底和高,利用“三角形的面积=底×高÷2”求出这个三角形的面积,最后根据“高=三角形的面积×2÷底”求出斜边上的高,据此解答。
【详解】分析可知,这个直角三角形的两条直角边分别是5cm和12cm,斜边是13cm。
5×12÷2
=60÷2
=30(cm2)
30×2÷13
=60÷13
≈5(cm)
所以,这个三角形的面积是30cm2,斜边上的高是5cm。
【点睛】掌握三角形的面积计算公式是解答题目的关键。
15. 10+2a 40
【分析】等腰三角形的周长=底长+腰长×2,三角形的面积=底×高÷2;据此将数据代入即可解答。
【详解】三角形的周长:10+2a(米)
三角形的面积:
10×8÷2
=80÷2
=40(平方米)
即这个三角形的周长是(10+2a)米,面积是40平方米。
16.1650
【分析】根据三角形的面积=底×高÷2,代入数据解答即可。
【详解】100×33÷2
=3300÷2
=1650(cm2)
所以小号红领巾的面积约是1650。
17.√
【分析】三角形面积公式:面积=底×高÷2,在直角三角形中,由于两条直角边是互相垂直的,所以一条直角边看作底,另一条直角边看作高,直角三角形面积等于两条直角边的长度乘积除以2,据此解答。
【详解】根据分析可知,直角三角形的面积等于两条直角边的长度乘积除以2。
原题干说法正确。
故答案为:√
18.√
【分析】图中每个正方形大小相等,可以设正方形的边长是1厘米,然后根据三角形的面积=底×高÷2,分别求出两个涂色三角形的面积,再比较,得出结论。
【详解】设正方形的边长是1厘米。
上面涂色三角形的面积:1×1÷2=0.5(平方厘米)
下面涂色三角形的面积:1×1÷2=0.5(平方厘米)
0.5=0.5
所以,两个涂色三角形的面积相等。
原题说法正确。
故答案为:√
19.√
【分析】等底等高的三角形面积相等。同样的正方形,则每个正方形的边长相等。甲三角形的底是2个正方形的边长,高是1个正方形的边长。乙三角形是底也是2个正方形的边长,高是1个正方形的边长。三角形的面积=底×高÷2。
【详解】设正方形的边长为1。
甲面积:2×1÷2=1
乙面积:2×1÷2=1
1=1
故答案为:√
20.√
【分析】三角形面积=底×高÷2,等底等高的两个三角形,形状不一定相同,面积相等,据此分析。
【详解】
如图,两个同底等高的三角形,形状不同,面积相等,所以原题说法正确。
故答案为:√
21.√
【分析】根据三角形面积公式:面积=底×高÷2,高=面积×2÷底,代入数据,求出高,再进行比较,即可解答。
【详解】16×2÷4
=32÷4
=8(cm)
一个三角形的面积是16cm2,它的底边是4cm,这个三角形的这条底上的高是8cm。
原题干说法正确。
故答案为:√
22.30平方分米
【分析】观察图形可知,空白三角形的底相当于长方形的长,高相当于长方形的宽,阴影部分的面积=长方形的面积-三角形的面积,根据长方形的面积公式:S=ab,三角形的面积公式:S=ah÷2,据此计算即可。
【详解】10×6-10×6÷2
=60-30
=30(平方分米)
23.30cm2
【分析】观察图形可知,阴影部分是一个底是(30-25)cm,高是12cm的三角形,根据三角形的面积=底×高÷2,代入数据计算即可。
【详解】(30-25)×12÷2
=5×12÷2
=60÷2
=30(cm2)
阴影部分的面积是30cm2。
24.4平方厘米
【分析】从图中可以看出,阴影部分是一个三角形,底是小正方形的边长,高是大正方形的边长,根据“三角形面积=底×高÷2”即可求出阴影部分的面积。
【详解】2×4÷2
=8÷2
=4(平方厘米)
所以,阴影部分的面积是4平方厘米。
25.3厘米
【分析】正方形ABCD的边长是6厘米,已知DE是EC长度的2倍,根据和倍问题公式:“和÷(倍数+1)=较小数,较小数×倍数=较大数”求出DE的长,再用三角形ADF的面积减去三角形ADE的面积,求出三角形DEF的面积,三角形ADF的底是6厘米、高是6厘米,三角形ADE的底是6厘米、高是4厘米,根据三角形的面积=底×高÷2,代入数据分别求出三角形ADF的面积和三角形ADE的面积,再相减求出三角形DEF的面积,CF边是三角形DEF以DE边为底的高,求CF,用三角形DEF面积的2倍除以DE即可解答。
【详解】6×6÷2
=36÷2
=18(平方厘米)
6÷(2+1)×2
=6÷3×2
=2×2
=4(厘米)
6×4÷2
=24÷2
=12(平方厘米)
18-12=6(平方厘米)
6×2÷4
=12÷4
=3(厘米)
答:CF的边长是3厘米。
26.2天
【分析】根据三角形的面积=底×高÷2,代入数据求出三角形菜地的面积是多少平方米,再根据1公顷=10000平方米,把平方米化成公顷,再根据除法的意义,用三角形的面积除以拖拉机每天耕地的公顷数即可解答。
【详解】500×1440÷2
=720000÷2
=360000(平方米)
360000平方米=36公顷
36÷18=2(天)
答:这块地2天才能耕完。
27.200克
【详解】1200÷(2×3÷2×2)=200(克)
28.5
【分析】如图,连接BD
△BED是△ABD面积的一半,△BDF是△BDC面积的一半,那么,可推出,据此解答即可。
【详解】10÷2=5
答:四边形EDFB的面积是5。
29.54平方分米
【分析】E,F是AC的三等分点,所以AF=EF=EC。因为EF+EC = FC ,所以2AF=FC。三角形BCF和三角形ABF的高相等,且2AF=FC,所以三角形BCF的面积是三角形ABF的2倍,三角形ABF的面积是108平方分米,用乘法计算,求出三角形BCF的面积;D是BC的中点,所以三角形FDC的面积是三角形BCF的面积的一半,用除法计算,求出三角形FDC的面积;又因为EF=EC,所以三角形CDE的面积是三角形FDC的面积的一半,用除法计算,求出三角形CDE的面积,据此解答。
【详解】108×2=216(平方分米)
216÷2=108(平方分米)
108÷2=54(平方分米)
答:三角形CDE的面积是54平方分米。
答案第1页,共2页
答案第1页,共2页
