1.4.2用空间向量研究距离、夹角问题 课件(共18张PPT)
文档属性
| 名称 | 1.4.2用空间向量研究距离、夹角问题 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 30.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-29 10:15:10 | ||
图片预览




文档简介
(共18张PPT)
1.4.2 用空间向量研究距离、夹角问题
第一章 空间向量与立体几何
教学目标
(1)学会求异面直线所成的角、直线与平面所成的角、二面角的向量法
(2)能够应用向量方法解决一些简单的立体几何问题
(3)提高分析与推理能力和空间想象能力
问题与例题
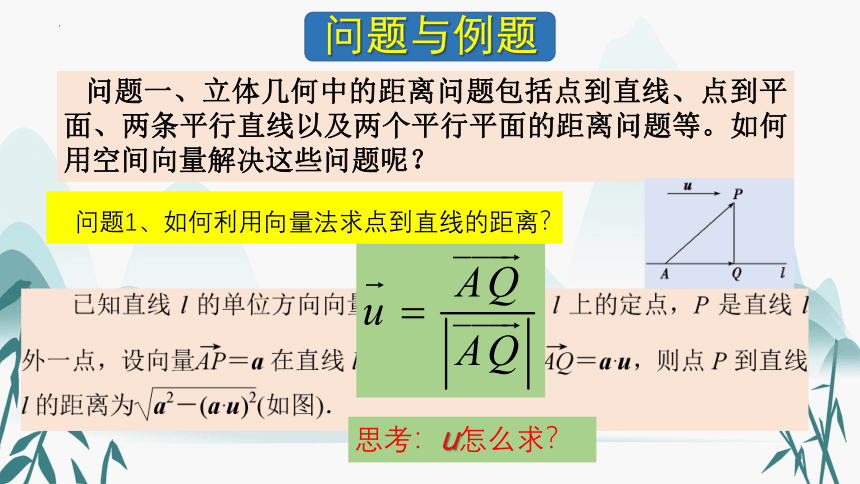
问题一、立体几何中的距离问题包括点到直线、点到平面、两条平行直线以及两个平行平面的距离问题等。如何用空间向量解决这些问题呢?
问题1、如何利用向量法求点到直线的距离?
思考:u怎么求?
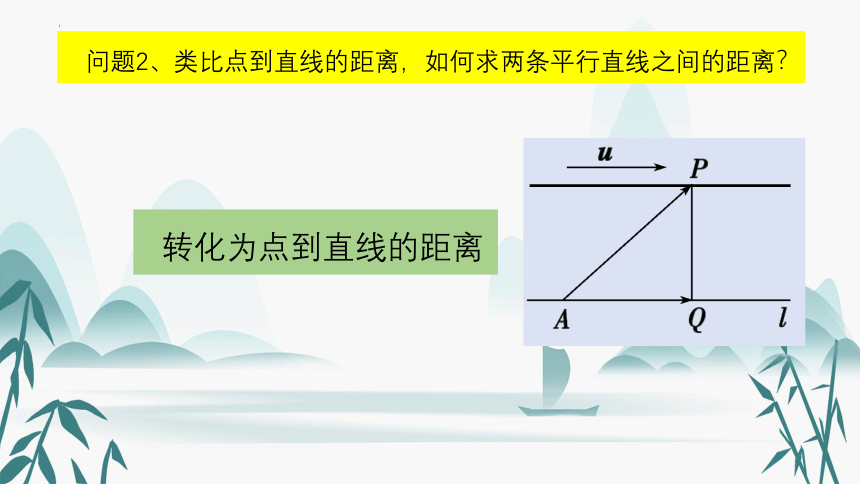
问题2、类比点到直线的距离,如何求两条平行直线之间的距离?
转化为点到直线的距离
例1、如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别为DD1、BB1的中点,求
(1)A1到直线B1E的距离
(2)直线FC1到直线AE的距离
E
F
变式练习
求点B到直线B1E的距离
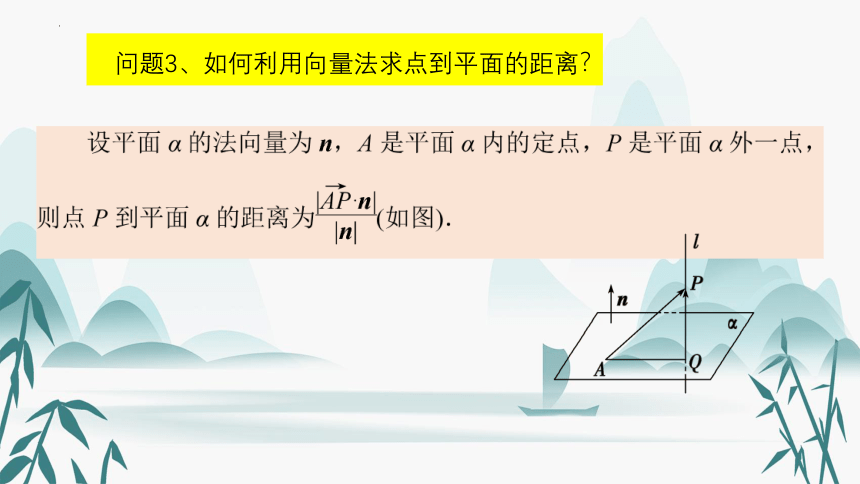
问题3、如何利用向量法求点到平面的距离?
问题4、类比利用向量法求点到平面的距离,如何求直线到平面、平面到平面的距离?
转化为点到平面的距离
例2、如图,正方体ABCD-A1B1C1D1的棱长为1,求:
(1)B到直线A1C1的距离
(2)D1到平面A1BD的距离.
(3)D1 C到平面A1BD的距离
(4)平面A1BD与平面B1CD1间的距离
变式练习
1、如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点
(1)求点B到直线AC1的距离
(2)求直线FC到平面AEC1的距离
E
F
2、如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在棱BB1上,EB1=1,D,F,G分别为CC1,B1C1,A1C1的中点,EF与B1D相交于点H.
(1)求证:B1D⊥平面ABD;
(2)求证:平面EGF∥平面ABD;
(3)求平面EGF与平面ABD的距离.
问题二、如何利用方向向量、法向量求异面直线的夹角、直线与平面所成夹角、平面与平面夹角、二面角?
1、异面直线的夹角
范围:[0°,90°]
2、直线与平面的夹角
范围:[0°,90°]
3、平面与平面的夹角
范围:[0°,90°]
C1
P
A
C
B
A1
B1
Q
R
例题3、如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q,R分别在棱AA1,BB1上,A1Q
=2AQ,BR=2RB1。求平面PQR与平面A1B1C1夹角的余弦值
1.已知向量m,n分别是直线l与平面α的方向向量、法向量,若cos〈m,n〉=
,则l与α所成的角为( )
A.30° B.60° C.150° D.120°
变式练习
B
2.已知平面α的法向量u=(1,0,-1),平面β的法向量v=(0,-1,1),则平面α与β的夹角为____.
3.如图,在正方体ABEF-DCE′F′中,M,N分别为AC,BF的中点,求
(1)求直线MN与直线AC的夹角余弦值
(2)求直线EN与平面MNB的夹角余弦值
(3)平面MNA与平面MNB的夹角的余弦值.
课堂小结
1、向量法求点到直线(平行直线)的距离.
2、向量法求点到平面(直线到平面、平面到平面)的距离.
3、向量法求直线与直线、直线与平面、平面与平面的夹角.
课后作业
课时作业(四)A组:教材P43第9、10题
B组:教材P43第15、18题
谢谢!
1.4.2 用空间向量研究距离、夹角问题
第一章 空间向量与立体几何
教学目标
(1)学会求异面直线所成的角、直线与平面所成的角、二面角的向量法
(2)能够应用向量方法解决一些简单的立体几何问题
(3)提高分析与推理能力和空间想象能力
问题与例题
问题一、立体几何中的距离问题包括点到直线、点到平面、两条平行直线以及两个平行平面的距离问题等。如何用空间向量解决这些问题呢?
问题1、如何利用向量法求点到直线的距离?
思考:u怎么求?
问题2、类比点到直线的距离,如何求两条平行直线之间的距离?
转化为点到直线的距离
例1、如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别为DD1、BB1的中点,求
(1)A1到直线B1E的距离
(2)直线FC1到直线AE的距离
E
F
变式练习
求点B到直线B1E的距离
问题3、如何利用向量法求点到平面的距离?
问题4、类比利用向量法求点到平面的距离,如何求直线到平面、平面到平面的距离?
转化为点到平面的距离
例2、如图,正方体ABCD-A1B1C1D1的棱长为1,求:
(1)B到直线A1C1的距离
(2)D1到平面A1BD的距离.
(3)D1 C到平面A1BD的距离
(4)平面A1BD与平面B1CD1间的距离
变式练习
1、如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点
(1)求点B到直线AC1的距离
(2)求直线FC到平面AEC1的距离
E
F
2、如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在棱BB1上,EB1=1,D,F,G分别为CC1,B1C1,A1C1的中点,EF与B1D相交于点H.
(1)求证:B1D⊥平面ABD;
(2)求证:平面EGF∥平面ABD;
(3)求平面EGF与平面ABD的距离.
问题二、如何利用方向向量、法向量求异面直线的夹角、直线与平面所成夹角、平面与平面夹角、二面角?
1、异面直线的夹角
范围:[0°,90°]
2、直线与平面的夹角
范围:[0°,90°]
3、平面与平面的夹角
范围:[0°,90°]
C1
P
A
C
B
A1
B1
Q
R
例题3、如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q,R分别在棱AA1,BB1上,A1Q
=2AQ,BR=2RB1。求平面PQR与平面A1B1C1夹角的余弦值
1.已知向量m,n分别是直线l与平面α的方向向量、法向量,若cos〈m,n〉=
,则l与α所成的角为( )
A.30° B.60° C.150° D.120°
变式练习
B
2.已知平面α的法向量u=(1,0,-1),平面β的法向量v=(0,-1,1),则平面α与β的夹角为____.
3.如图,在正方体ABEF-DCE′F′中,M,N分别为AC,BF的中点,求
(1)求直线MN与直线AC的夹角余弦值
(2)求直线EN与平面MNB的夹角余弦值
(3)平面MNA与平面MNB的夹角的余弦值.
课堂小结
1、向量法求点到直线(平行直线)的距离.
2、向量法求点到平面(直线到平面、平面到平面)的距离.
3、向量法求直线与直线、直线与平面、平面与平面的夹角.
课后作业
课时作业(四)A组:教材P43第9、10题
B组:教材P43第15、18题
谢谢!
