第五章 二元一次方程组 全章热门考点整合应用(含答案) 2024-2025学年北师大版八年级数学上册
文档属性
| 名称 | 第五章 二元一次方程组 全章热门考点整合应用(含答案) 2024-2025学年北师大版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 209.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-29 09:27:43 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 二元一次方程组 全章热门考点整合应用
核心考点整合
考点1 二元一次方程(组) 的有关概念
1.下列方程组:①(②2x+y=15,④ ,其中是二元一次方程组的是 ( )
A.①② B.③④
C.①②④ D.①②③
2. 下列四组数值是二元一次方程 2x—y=6 的解的是 ( )
3.已知m为正整数,且关于x,y的二元一次方程组 有整数解,则m的值为 ( )
A.1 B.2 C.3 D.7
4.以方程组 的解为坐标的点(x,y)在第 象限内.
考点 2 三元一次方程组
5.下列方程组中是三元一次方程组的是 ( )
考点 3 方程组的解法
6.解下列方程组:
7. 在等式 中,当x=-1时,y=3;当x=0时,y=1,当x=1时,y=1,求这个等式中a,b,c的值.
考点4 二元一次方程的应用
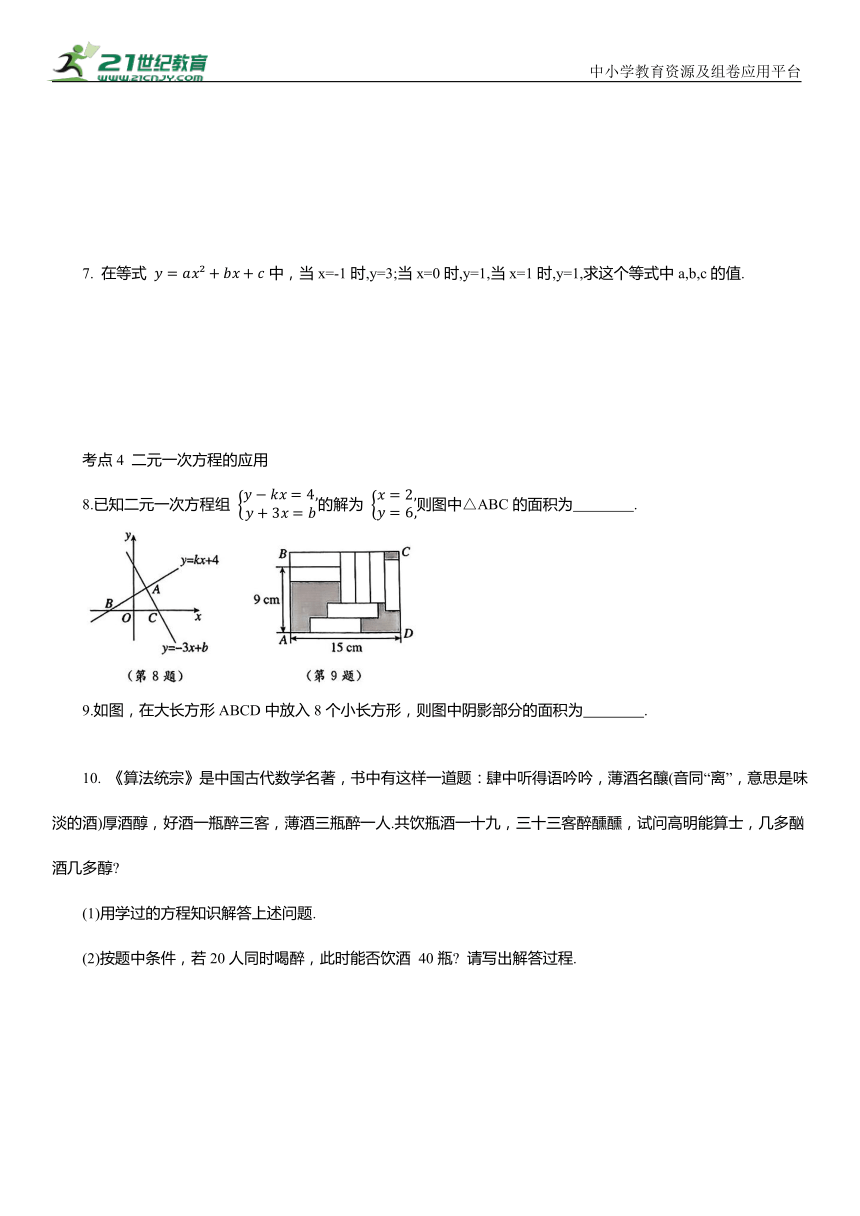
8.已知二元一次方程组 的解为 则图中△ABC的面积为 .
9.如图,在大长方形ABCD中放入8个小长方形,则图中阴影部分的面积为 .
10. 《算法统宗》是中国古代数学名著,书中有这样一道题:肆中听得语吟吟,薄酒名釀(音同“离”,意思是味淡的酒)厚酒醇,好酒一瓶醉三客,薄酒三瓶醉一人.共饮瓶酒一十九,三十三客醉醺醺,试问高明能算士,几多酗酒几多醇
(1)用学过的方程知识解答上述问题.
(2)按题中条件,若20人同时喝醉,此时能否饮酒 40瓶 请写出解答过程.
考点5 二元一次方程 (组) 与一次函数的关系
11.如图,在平面直角坐标系xOy中,直线 l : 和 相交于点 A.
(1)观察图象,直接写出方程组 的解;
(2)若直线 与 y轴的交点为(0,-4),求直线 l 的表达式.
思想方法整合
思想1 建模思想
12. 课余活动中,小杰、小明和小丽一起玩飞镖游戏,飞镖盘上 A区域分值和 B区域分值不同,每人投5 次飞镖,其落点如图所示,已知小杰和小明的5次飞镖总分分别为39分和43 分,则小丽的5次飞镖总分为 分.
思想 2 整体思想
13. 【数学问题】 解 方 程 组
【思路分析】小明观察后发现方程①的左边是x+y,而方程②的括号里也是x+y,他想到可以把x+y视为一个整体,把方程①直接代入到方程②中,这样,就可以将方程②直接转化为一元一次方程,从而达到“消元”的目的.
(1)【完成解答】请你按照小明的思路,完成解方程组的过程;
(2)已知x,y,z满足 试求 z的值.
1 C 2. B
3 B 【点拨】 ①+②,得(3+m)x=10,解得 将 代入②得 因为原方程组有整数解,所以3+m=±1或±5,解得 m=-2 或-4或2或-8.又因为m是正整数,所以m=2.
4.一 5. C
6.【解】(1){x=x+y=x,0,①→3=8,0。7y=-14,解得y=—2.将y=—2代入①,得2x—2=2,解得x=2.所以原方程组的解为
由①,得3x+4y=36,③
由②得3x-2y=9,④
③--④,得6y=27,解得
将 代入④,得3x-9=9,解得x=6.
所以原方程组的解为
7 【解】由题意,得 解得
8.24 【点拨】因为二元一次方程组 的解为 所以函数y= kx+4 与函数 y=-3x+b的交点为(2,6).将(2,6)代入y= kx+4,得6=2k+4,解得k=1.将(2,6)代入y=-3x+b,得6=-6+b,解得b=12,所以两个函数的表达式分别为y=x+4与y=-3x+12.对于y=x+4,令y=0,则x+4=0,解得x=-4;对于y=-3x+12,令 y=0,则-3x+12=0,解得x=4,所以B(-4,0),C(4,0),所以BC=8,所以△ABC的面积 8×6=24.
9.53 cm 【点拨】设小长方形的长为 x cm,宽为 y cm,依 题意,得 解得
所以图中阴影部分面积为15×(9+y)-8xy=15×(9+2)-8×7×2=53(cm ).
10.【解】(1)设共喝了好酒 x 瓶,薄酒 y瓶,由题意得 解得 所以共喝了好酒10瓶,薄酒9瓶.
(2)不能,设共喝了好酒 m 瓶,薄酒 n 瓶,由题意,得 解得 因为 m,n必须是非负整数,所以20人同时喝醉,此时不能饮酒40瓶.
11.【解】(1)方程组的解为
(2)由题意,得 解得 所以直线l 的表达式为y=1.5x-4.
12.37 【点拨】设A区每镖得x分,B区每镖得y分,根据题意,得 解得 所以小丽的5次飞镖总分为4×7+9=37(分).
13. 【解】(1)把①代入②,得5x-2×2=6,解得x=2.将x=2代入①,得2+y=2,解得y=0,所以原方程组的解为
由②知x+4y=19-z,③
①可变形为3(x+4y)-2z=47,④
将③代入④,得3×(19-z)-2z=47,
解得 z=2.
第五章 二元一次方程组 全章热门考点整合应用
核心考点整合
考点1 二元一次方程(组) 的有关概念
1.下列方程组:①(②2x+y=15,④ ,其中是二元一次方程组的是 ( )
A.①② B.③④
C.①②④ D.①②③
2. 下列四组数值是二元一次方程 2x—y=6 的解的是 ( )
3.已知m为正整数,且关于x,y的二元一次方程组 有整数解,则m的值为 ( )
A.1 B.2 C.3 D.7
4.以方程组 的解为坐标的点(x,y)在第 象限内.
考点 2 三元一次方程组
5.下列方程组中是三元一次方程组的是 ( )
考点 3 方程组的解法
6.解下列方程组:
7. 在等式 中,当x=-1时,y=3;当x=0时,y=1,当x=1时,y=1,求这个等式中a,b,c的值.
考点4 二元一次方程的应用
8.已知二元一次方程组 的解为 则图中△ABC的面积为 .
9.如图,在大长方形ABCD中放入8个小长方形,则图中阴影部分的面积为 .
10. 《算法统宗》是中国古代数学名著,书中有这样一道题:肆中听得语吟吟,薄酒名釀(音同“离”,意思是味淡的酒)厚酒醇,好酒一瓶醉三客,薄酒三瓶醉一人.共饮瓶酒一十九,三十三客醉醺醺,试问高明能算士,几多酗酒几多醇
(1)用学过的方程知识解答上述问题.
(2)按题中条件,若20人同时喝醉,此时能否饮酒 40瓶 请写出解答过程.
考点5 二元一次方程 (组) 与一次函数的关系
11.如图,在平面直角坐标系xOy中,直线 l : 和 相交于点 A.
(1)观察图象,直接写出方程组 的解;
(2)若直线 与 y轴的交点为(0,-4),求直线 l 的表达式.
思想方法整合
思想1 建模思想
12. 课余活动中,小杰、小明和小丽一起玩飞镖游戏,飞镖盘上 A区域分值和 B区域分值不同,每人投5 次飞镖,其落点如图所示,已知小杰和小明的5次飞镖总分分别为39分和43 分,则小丽的5次飞镖总分为 分.
思想 2 整体思想
13. 【数学问题】 解 方 程 组
【思路分析】小明观察后发现方程①的左边是x+y,而方程②的括号里也是x+y,他想到可以把x+y视为一个整体,把方程①直接代入到方程②中,这样,就可以将方程②直接转化为一元一次方程,从而达到“消元”的目的.
(1)【完成解答】请你按照小明的思路,完成解方程组的过程;
(2)已知x,y,z满足 试求 z的值.
1 C 2. B
3 B 【点拨】 ①+②,得(3+m)x=10,解得 将 代入②得 因为原方程组有整数解,所以3+m=±1或±5,解得 m=-2 或-4或2或-8.又因为m是正整数,所以m=2.
4.一 5. C
6.【解】(1){x=x+y=x,0,①→3=8,0。7y=-14,解得y=—2.将y=—2代入①,得2x—2=2,解得x=2.所以原方程组的解为
由①,得3x+4y=36,③
由②得3x-2y=9,④
③--④,得6y=27,解得
将 代入④,得3x-9=9,解得x=6.
所以原方程组的解为
7 【解】由题意,得 解得
8.24 【点拨】因为二元一次方程组 的解为 所以函数y= kx+4 与函数 y=-3x+b的交点为(2,6).将(2,6)代入y= kx+4,得6=2k+4,解得k=1.将(2,6)代入y=-3x+b,得6=-6+b,解得b=12,所以两个函数的表达式分别为y=x+4与y=-3x+12.对于y=x+4,令y=0,则x+4=0,解得x=-4;对于y=-3x+12,令 y=0,则-3x+12=0,解得x=4,所以B(-4,0),C(4,0),所以BC=8,所以△ABC的面积 8×6=24.
9.53 cm 【点拨】设小长方形的长为 x cm,宽为 y cm,依 题意,得 解得
所以图中阴影部分面积为15×(9+y)-8xy=15×(9+2)-8×7×2=53(cm ).
10.【解】(1)设共喝了好酒 x 瓶,薄酒 y瓶,由题意得 解得 所以共喝了好酒10瓶,薄酒9瓶.
(2)不能,设共喝了好酒 m 瓶,薄酒 n 瓶,由题意,得 解得 因为 m,n必须是非负整数,所以20人同时喝醉,此时不能饮酒40瓶.
11.【解】(1)方程组的解为
(2)由题意,得 解得 所以直线l 的表达式为y=1.5x-4.
12.37 【点拨】设A区每镖得x分,B区每镖得y分,根据题意,得 解得 所以小丽的5次飞镖总分为4×7+9=37(分).
13. 【解】(1)把①代入②,得5x-2×2=6,解得x=2.将x=2代入①,得2+y=2,解得y=0,所以原方程组的解为
由②知x+4y=19-z,③
①可变形为3(x+4y)-2z=47,④
将③代入④,得3×(19-z)-2z=47,
解得 z=2.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
