4.4一次函数的应用第2课时 一次函数的应用同步练习 2024-2025学年北师大版八年级数学上册(含答案)
文档属性
| 名称 | 4.4一次函数的应用第2课时 一次函数的应用同步练习 2024-2025学年北师大版八年级数学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 626.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-29 00:00:00 | ||
图片预览



文档简介
第2课时 一次函数的应用(1)
基础题目Q
1.若一元一次方程 ax--b=0的解是x=3,则函数y= ax--b的图象与x轴的交点坐标为 ( )
A.(3,0) B.(-3,0)
C.(a,0) D.(-b,0)
2.已知一次函数y= ax+b的图象如图所示,则方程 ax+b=1的解为x= ( )
A.4
B.2
C.0
D. --1
3. 在物理实验课上,小鹏利用滑轮组及相关器材进行实验,他把得到的拉力F(N)和所悬挂物体的重力G(N)的几组数据用电脑绘制成如图所示的图象(不计绳重和摩擦),请你根据图象判断以下结论正确的有( )
①物体的拉力随着重力的增加而增大;
②当物体的重力G=7 N.时,拉力F=2.2 N;
③拉力F与重力G 成正比例函数关系;
④当滑轮组不悬挂物体时,所用拉力为0.5N.
A.①② B.②④
C.①④ D.③④
4.弹簧的长度y( cm)与所挂物体的质量x( kg)之间是一次函数关系,其图象如图所示,则弹簧本身的长度为
5. 直线l:y=2x-m过点 P(m,2).
(1)求直线l的表达式;
(2)方程2x--m=0的解为 .
综合应用题
6. 李大爷以每千克2.1元的价格批发了一批南瓜到镇上出售,为了方便,他带了一些零钱备用,他先按市场价售出一些后,由于滞销,然后他每千克降低1.6元将剩余部分全部售出,他手中持有的钱数 y元(含备用零钱)与售出南瓜千克数x的关系如图所示,下列说法中正确的有 ( )
①李大爷自带的零钱是50元;
②降价前他每千克南瓜出售的价格是 4.1元;
③这批南瓜一共有 160千克;
④李大爷销售这批南瓜一共赚了 194元.
A.1 个 B.2 个 C.3 个 D.4 个
7. 在弹性限度内,某弹簧长度 y( cm)与所挂物体质量x( kg)间有下表的关系.下列说法不正确的是 ( )
x/ kg 0 1 2 3 4
y/ cm 15 17 19 21 23
A.因变量y是自变量x 的一次函数
B.当弹簧长度为18 cm时,所挂物体的质量为0.5kg
C.随着所挂物体质量的增加,弹簧长度逐渐变长
D.所挂物体的质量每增加 1 kg,弹簧长度增加 2 cm
8.如图,一次函数y=2x和y= ax+4 的图象相交于点A(m,3),则方程 ax+4=0的解为( )
A. x=6 B. x=3
C. x=-6 D. x=-3
9.某生物小组观察一植物生长,得到植物高度 y(单位:厘米)与观察时间x(单位:天)之间的关系,并画出如图所示的图象(AC是线段,射线 CD 平行于 x 轴).在第 天后植物的高度不变,该植物最高为 厘米.
10.某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,如图,折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段 DE 表示的函数关系中时间每增加1天,日销售量减少5件.
(1)第17天的日销售量是 件,日销售利润是 元;
(2)求试销售期间日销售利润的最大值.
创新拓展题
11.如图①所示,某乘客乘高速列车从甲地经过乙地到丙地,列车匀速行驶,图②为列车离乙地的距离y(千米)与行驶时间x(小时)之间的函数关系图象.
(1)填空:甲、丙两地相距 千米,高速列车的速度为 千米/小时.
(2)当高速列车从甲地到丙地时,求高速列车离乙地的距离 y 与行驶时间x 之间的函数关系式.
(3)在整个行驶过程中,请问高速列车离乙地的距离在 100千米以内的时间有多长
一次函数的应用(2)
基础题目
1. 如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶路程随时间变化的图象.则下列结论错误的是( )
A.轮船的速度为 20 千米/小时
B.快艇的速度为 40 千米/小时
C.轮船比快艇先出发 2 小时
D.快艇到达乙港用了6 小时
2. 《九章算术》中记载:今有坦高九尺,瓜生其上,蔓日长七寸;弧生其下,蔓日长一尺.问几何日相逢 (大意是有一道墙,高9尺,上面种一株瓜,瓜蔓向下伸,每天长7寸,地上种着瓠向上长,每天长1尺,问瓜蔓,瓠蔓要多少天才相遇).如图是瓜蔓与瓠蔓离地面的高度h(单位:尺)关于生长时间x(单位:天)的函数图象,则由图可知两图象交点 P的横坐标是(注:1尺=10寸) ( )
A. B.5
D.30
3. 李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温y(℃)与加热时间x(s)之间近似满足一次函数关系,根据记录的数据,画函数图象如图.
(1)加热前水温是 ;
(2)求乙水壶中水温y关于加热时间x的关系式;
(3)当甲壶中水温刚达到80 ℃时,乙壶中水温是
综合应用题
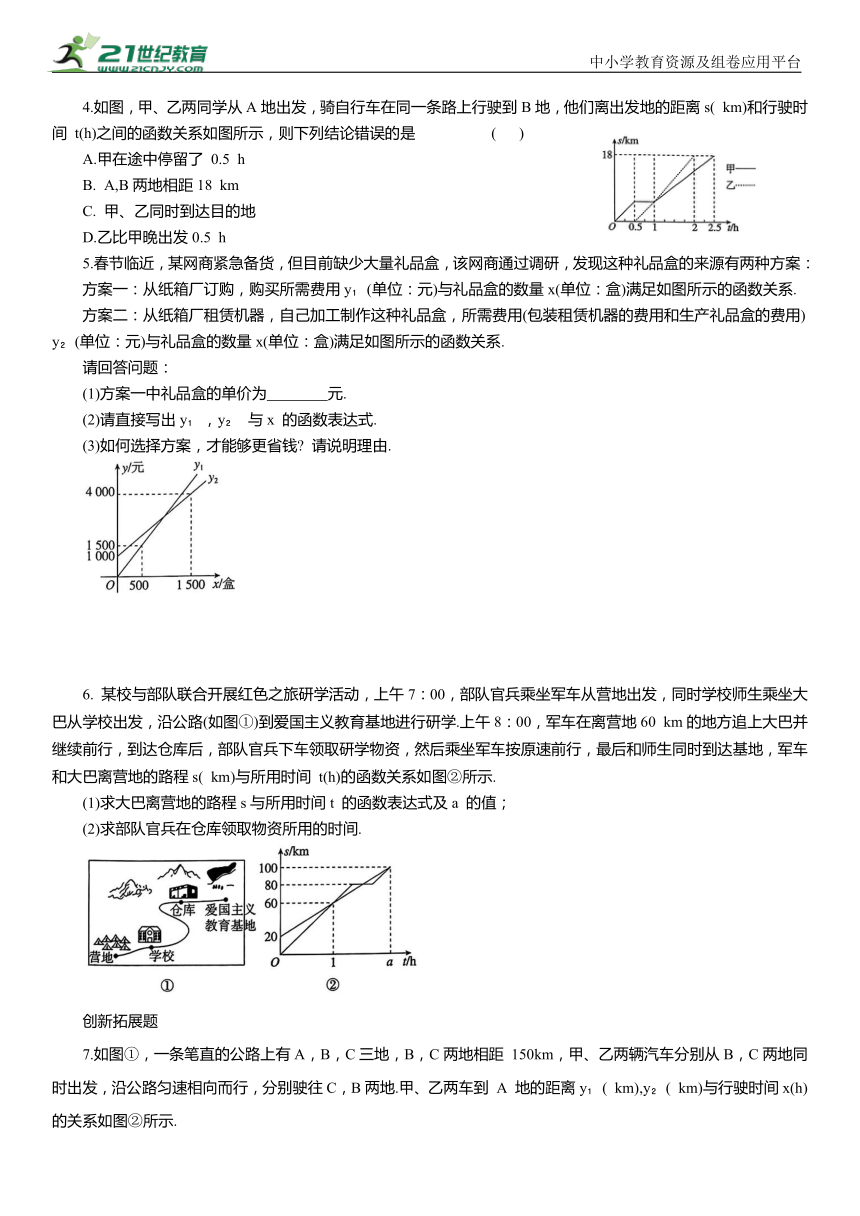
4.如图,甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s( km)和行驶时间 t(h)之间的函数关系如图所示,则下列结论错误的是 ( )
A.甲在途中停留了 0.5 h
B. A,B两地相距18 km
C. 甲、乙同时到达目的地
D.乙比甲晚出发0.5 h
5.春节临近,某网商紧急备货,但目前缺少大量礼品盒,该网商通过调研,发现这种礼品盒的来源有两种方案:
方案一:从纸箱厂订购,购买所需费用y (单位:元)与礼品盒的数量x(单位:盒)满足如图所示的函数关系.
方案二:从纸箱厂租赁机器,自己加工制作这种礼品盒,所需费用(包装租赁机器的费用和生产礼品盒的费用)y (单位:元)与礼品盒的数量x(单位:盒)满足如图所示的函数关系.
请回答问题:
(1)方案一中礼品盒的单价为 元.
(2)请直接写出y ,y 与x 的函数表达式.
(3)如何选择方案,才能够更省钱 请说明理由.
6. 某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图①)到爱国主义教育基地进行研学.上午8:00,军车在离营地60 km的地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s( km)与所用时间 t(h)的函数关系如图②所示.
(1)求大巴离营地的路程s与所用时间t 的函数表达式及a 的值;
(2)求部队官兵在仓库领取物资所用的时间.
创新拓展题
7.如图①,一条笔直的公路上有A,B,C三地,B,C两地相距 150km,甲、乙两辆汽车分别从B,C两地同时出发,沿公路匀速相向而行,分别驶往C,B两地.甲、乙两车到 A 地的距离y ( km),y ( km)与行驶时间x(h)的关系如图②所示.
根据图象进行以下探究:
(1)请在图①中标出A地的位置,并作简要说明.
(2)甲的速度为 km/h,乙的速度为 km/h.
(3)求图②中M点的坐标,并解释该点的实际意义.
(4)在图②中补全甲车到达C地的函数图象,并求出甲车到A地的距离y 与行驶时间x的函数关系式.
中小学教育资源及组卷应用平台
(5)出发多长时间,甲、乙两车距 A 地的距离相等
第2课时 一次函数的应用(1)
1. A 2. A 3. C 4.10 cm
5. 【解】(1)因为直线l:y=2x-m过点P(m,2),所以2=2m-m,解得m=2.
所以直线l的表达式为y=2x-2.
(2)x=1
6. B
7. B 【点拨】由表格,得y=2x+15(0≤x≤a,a 为弹簧秤的最大限度),故A是正确的;当y=18时,2x+15=18,解得x=1.5,故B是错误的;在弹性限度内,随所挂物品的质量的增加,弹簧长度逐渐变长,故C 是正确的;在弹性限度内,所挂物体的质量每增加 1 kg,弹簧长度增加2cm ,故 D是正确的.
8. A 【点拨】因为点A在直线y=2x上,所以3=2m,解得 所以点A的坐标为 ,3).因为一次函数 y=2和、y= ax+4的图象相交于点A(m,3),所以. 解得 所以方程 ax+4=0可化为 解得x=6.
50;16 【点拨】因为CD∥x轴,所以从第50天开始植物 -的高度不变.设线段AC的表达式为y= kx+b(k≠0,0≤x≤50).因为A(0,6),B(30,12),所以b=6,30k+b=12,解得 所以线段 AC的表达式为 x≤50).当x=50时 所以该植物最高为 16厘米.
10.【解】(1)340;680
(2)因为直线OD过点(17,340),
所以直线OD的表达式为y=20x.
设直线 DE的表达式为y=-5x+b,
将(22,340)代入y=-5x+b,解得b=450.
所以直线DE的表达式为y=-5x+450.
令-5x+450=20x,解得x=18.
在y=20x中,当x=18时,y=360.
所以折线ODE 的最高点D 的坐标为(18,360).
360×(8-6)=720(元),
所以当x=18时,日销售利润最大,最大利润为 720元.
11.【解】(1)1 050;300
(2)当0≤x≤3时,设高速列车离乙地的距离y与行驶时间x之间的函数关系式为y= kx+b,
把(0,900),(3,0)代入,得b=900,3k+b=0,解得k=-300.
因此 y = - 300x + 900(0≤x≤3).
如 图, 因 为 3 + 150 ÷300=3.5(小时),
所以点A的坐标为(3.5,150).
因为高速到车的速度是900÷3=300(千米/时),
所以当3(3)在y=-300x+900中,当y=100时,有-300x+900=100,解得
在y=300x-900中,当y=100时,有300x-900=100,解得
(小时),
所以高速列车离乙地的距离在 100千米以内的时间为 小时.
一次函数的应用(2)
1. D 2. C
3.【解】(1)20℃
(2)设乙壶中水温y关于加热时间x的关系式为y= kx+b,根据题意,得20=b,① 80=160k+b.②将①代入②,得 所以乙壶中水温y关于加热时间x 的关系式为
(3)65 ℃
4. C 【点拨】A.甲在0.5 h至 1 h之间,s没有变化,说明甲在途中停留了0.5h,故A 选项不合题意;B.由图象易得 A,B两地的距离是18 km,故 B选项不合题意;C.由图象可得,乙先到达目的地,故C选项符合题意;D.由图象可得,乙比甲晚出发0.5h,故D选项不合题意.
5.【解】(1)3
(2)y =3x,y =2x+1000.【点拨】设y 的函数表达式为
因为函数图象经过点(500,1 500),
所以1500=500k ,解得/k =3,
所以 y 的函数表达式为y =3x.
设 y 的函数表达式为
因为函数图象经过点(0,1000)和(1 500,4 000),
所以 ,解得
所以 y 的函数表达式为 y =2x+1000.
(3)令3x=2x+1000,解得x=1000,所以当x=1000时,两种方案同样省钱;当x<1000时,选择方案一更省钱;当x>1000时,选择方案二更省钱.
6.【解】(1)大巴的速度为 所以s=20+40t.当s=100时,100=20+40a,解得a=2.则大巴离营地的路程s与所用时间t 的函数表达式为s=20+40t,a的值为2.
(2)由函数图象可得,军车速度为60÷1=60( km/h),设部队官兵在仓库领取物资所用的时间为 xh,根据题意,得60(2-x)=100,解得
所以部队官兵在仓库领取物资所用的时间 h
7.【解】(1)由函数图象可以得出 A点在线段 BC上且AB=60 km,如图①所示.
(2)60;75
,所以M点的坐标为 ,0),M点的际意义是乙车到达A 地的时间 h
(4)150÷60=2.5(h),补全图象如图②.
当0≤x≤1时,y =60-60x;
当1所以
(5)设出发 xh时,甲、乙两车距A地的距离相等,由题意,得60x—60=75x—90 或60x—60=90—75x,解得.
所以出发2h h时,甲、乙两车距A地的距离相等
基础题目Q
1.若一元一次方程 ax--b=0的解是x=3,则函数y= ax--b的图象与x轴的交点坐标为 ( )
A.(3,0) B.(-3,0)
C.(a,0) D.(-b,0)
2.已知一次函数y= ax+b的图象如图所示,则方程 ax+b=1的解为x= ( )
A.4
B.2
C.0
D. --1
3. 在物理实验课上,小鹏利用滑轮组及相关器材进行实验,他把得到的拉力F(N)和所悬挂物体的重力G(N)的几组数据用电脑绘制成如图所示的图象(不计绳重和摩擦),请你根据图象判断以下结论正确的有( )
①物体的拉力随着重力的增加而增大;
②当物体的重力G=7 N.时,拉力F=2.2 N;
③拉力F与重力G 成正比例函数关系;
④当滑轮组不悬挂物体时,所用拉力为0.5N.
A.①② B.②④
C.①④ D.③④
4.弹簧的长度y( cm)与所挂物体的质量x( kg)之间是一次函数关系,其图象如图所示,则弹簧本身的长度为
5. 直线l:y=2x-m过点 P(m,2).
(1)求直线l的表达式;
(2)方程2x--m=0的解为 .
综合应用题
6. 李大爷以每千克2.1元的价格批发了一批南瓜到镇上出售,为了方便,他带了一些零钱备用,他先按市场价售出一些后,由于滞销,然后他每千克降低1.6元将剩余部分全部售出,他手中持有的钱数 y元(含备用零钱)与售出南瓜千克数x的关系如图所示,下列说法中正确的有 ( )
①李大爷自带的零钱是50元;
②降价前他每千克南瓜出售的价格是 4.1元;
③这批南瓜一共有 160千克;
④李大爷销售这批南瓜一共赚了 194元.
A.1 个 B.2 个 C.3 个 D.4 个
7. 在弹性限度内,某弹簧长度 y( cm)与所挂物体质量x( kg)间有下表的关系.下列说法不正确的是 ( )
x/ kg 0 1 2 3 4
y/ cm 15 17 19 21 23
A.因变量y是自变量x 的一次函数
B.当弹簧长度为18 cm时,所挂物体的质量为0.5kg
C.随着所挂物体质量的增加,弹簧长度逐渐变长
D.所挂物体的质量每增加 1 kg,弹簧长度增加 2 cm
8.如图,一次函数y=2x和y= ax+4 的图象相交于点A(m,3),则方程 ax+4=0的解为( )
A. x=6 B. x=3
C. x=-6 D. x=-3
9.某生物小组观察一植物生长,得到植物高度 y(单位:厘米)与观察时间x(单位:天)之间的关系,并画出如图所示的图象(AC是线段,射线 CD 平行于 x 轴).在第 天后植物的高度不变,该植物最高为 厘米.
10.某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,如图,折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段 DE 表示的函数关系中时间每增加1天,日销售量减少5件.
(1)第17天的日销售量是 件,日销售利润是 元;
(2)求试销售期间日销售利润的最大值.
创新拓展题
11.如图①所示,某乘客乘高速列车从甲地经过乙地到丙地,列车匀速行驶,图②为列车离乙地的距离y(千米)与行驶时间x(小时)之间的函数关系图象.
(1)填空:甲、丙两地相距 千米,高速列车的速度为 千米/小时.
(2)当高速列车从甲地到丙地时,求高速列车离乙地的距离 y 与行驶时间x 之间的函数关系式.
(3)在整个行驶过程中,请问高速列车离乙地的距离在 100千米以内的时间有多长
一次函数的应用(2)
基础题目
1. 如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶路程随时间变化的图象.则下列结论错误的是( )
A.轮船的速度为 20 千米/小时
B.快艇的速度为 40 千米/小时
C.轮船比快艇先出发 2 小时
D.快艇到达乙港用了6 小时
2. 《九章算术》中记载:今有坦高九尺,瓜生其上,蔓日长七寸;弧生其下,蔓日长一尺.问几何日相逢 (大意是有一道墙,高9尺,上面种一株瓜,瓜蔓向下伸,每天长7寸,地上种着瓠向上长,每天长1尺,问瓜蔓,瓠蔓要多少天才相遇).如图是瓜蔓与瓠蔓离地面的高度h(单位:尺)关于生长时间x(单位:天)的函数图象,则由图可知两图象交点 P的横坐标是(注:1尺=10寸) ( )
A. B.5
D.30
3. 李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温y(℃)与加热时间x(s)之间近似满足一次函数关系,根据记录的数据,画函数图象如图.
(1)加热前水温是 ;
(2)求乙水壶中水温y关于加热时间x的关系式;
(3)当甲壶中水温刚达到80 ℃时,乙壶中水温是
综合应用题
4.如图,甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s( km)和行驶时间 t(h)之间的函数关系如图所示,则下列结论错误的是 ( )
A.甲在途中停留了 0.5 h
B. A,B两地相距18 km
C. 甲、乙同时到达目的地
D.乙比甲晚出发0.5 h
5.春节临近,某网商紧急备货,但目前缺少大量礼品盒,该网商通过调研,发现这种礼品盒的来源有两种方案:
方案一:从纸箱厂订购,购买所需费用y (单位:元)与礼品盒的数量x(单位:盒)满足如图所示的函数关系.
方案二:从纸箱厂租赁机器,自己加工制作这种礼品盒,所需费用(包装租赁机器的费用和生产礼品盒的费用)y (单位:元)与礼品盒的数量x(单位:盒)满足如图所示的函数关系.
请回答问题:
(1)方案一中礼品盒的单价为 元.
(2)请直接写出y ,y 与x 的函数表达式.
(3)如何选择方案,才能够更省钱 请说明理由.
6. 某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图①)到爱国主义教育基地进行研学.上午8:00,军车在离营地60 km的地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s( km)与所用时间 t(h)的函数关系如图②所示.
(1)求大巴离营地的路程s与所用时间t 的函数表达式及a 的值;
(2)求部队官兵在仓库领取物资所用的时间.
创新拓展题
7.如图①,一条笔直的公路上有A,B,C三地,B,C两地相距 150km,甲、乙两辆汽车分别从B,C两地同时出发,沿公路匀速相向而行,分别驶往C,B两地.甲、乙两车到 A 地的距离y ( km),y ( km)与行驶时间x(h)的关系如图②所示.
根据图象进行以下探究:
(1)请在图①中标出A地的位置,并作简要说明.
(2)甲的速度为 km/h,乙的速度为 km/h.
(3)求图②中M点的坐标,并解释该点的实际意义.
(4)在图②中补全甲车到达C地的函数图象,并求出甲车到A地的距离y 与行驶时间x的函数关系式.
中小学教育资源及组卷应用平台
(5)出发多长时间,甲、乙两车距 A 地的距离相等
第2课时 一次函数的应用(1)
1. A 2. A 3. C 4.10 cm
5. 【解】(1)因为直线l:y=2x-m过点P(m,2),所以2=2m-m,解得m=2.
所以直线l的表达式为y=2x-2.
(2)x=1
6. B
7. B 【点拨】由表格,得y=2x+15(0≤x≤a,a 为弹簧秤的最大限度),故A是正确的;当y=18时,2x+15=18,解得x=1.5,故B是错误的;在弹性限度内,随所挂物品的质量的增加,弹簧长度逐渐变长,故C 是正确的;在弹性限度内,所挂物体的质量每增加 1 kg,弹簧长度增加2cm ,故 D是正确的.
8. A 【点拨】因为点A在直线y=2x上,所以3=2m,解得 所以点A的坐标为 ,3).因为一次函数 y=2和、y= ax+4的图象相交于点A(m,3),所以. 解得 所以方程 ax+4=0可化为 解得x=6.
50;16 【点拨】因为CD∥x轴,所以从第50天开始植物 -的高度不变.设线段AC的表达式为y= kx+b(k≠0,0≤x≤50).因为A(0,6),B(30,12),所以b=6,30k+b=12,解得 所以线段 AC的表达式为 x≤50).当x=50时 所以该植物最高为 16厘米.
10.【解】(1)340;680
(2)因为直线OD过点(17,340),
所以直线OD的表达式为y=20x.
设直线 DE的表达式为y=-5x+b,
将(22,340)代入y=-5x+b,解得b=450.
所以直线DE的表达式为y=-5x+450.
令-5x+450=20x,解得x=18.
在y=20x中,当x=18时,y=360.
所以折线ODE 的最高点D 的坐标为(18,360).
360×(8-6)=720(元),
所以当x=18时,日销售利润最大,最大利润为 720元.
11.【解】(1)1 050;300
(2)当0≤x≤3时,设高速列车离乙地的距离y与行驶时间x之间的函数关系式为y= kx+b,
把(0,900),(3,0)代入,得b=900,3k+b=0,解得k=-300.
因此 y = - 300x + 900(0≤x≤3).
如 图, 因 为 3 + 150 ÷300=3.5(小时),
所以点A的坐标为(3.5,150).
因为高速到车的速度是900÷3=300(千米/时),
所以当3
在y=300x-900中,当y=100时,有300x-900=100,解得
(小时),
所以高速列车离乙地的距离在 100千米以内的时间为 小时.
一次函数的应用(2)
1. D 2. C
3.【解】(1)20℃
(2)设乙壶中水温y关于加热时间x的关系式为y= kx+b,根据题意,得20=b,① 80=160k+b.②将①代入②,得 所以乙壶中水温y关于加热时间x 的关系式为
(3)65 ℃
4. C 【点拨】A.甲在0.5 h至 1 h之间,s没有变化,说明甲在途中停留了0.5h,故A 选项不合题意;B.由图象易得 A,B两地的距离是18 km,故 B选项不合题意;C.由图象可得,乙先到达目的地,故C选项符合题意;D.由图象可得,乙比甲晚出发0.5h,故D选项不合题意.
5.【解】(1)3
(2)y =3x,y =2x+1000.【点拨】设y 的函数表达式为
因为函数图象经过点(500,1 500),
所以1500=500k ,解得/k =3,
所以 y 的函数表达式为y =3x.
设 y 的函数表达式为
因为函数图象经过点(0,1000)和(1 500,4 000),
所以 ,解得
所以 y 的函数表达式为 y =2x+1000.
(3)令3x=2x+1000,解得x=1000,所以当x=1000时,两种方案同样省钱;当x<1000时,选择方案一更省钱;当x>1000时,选择方案二更省钱.
6.【解】(1)大巴的速度为 所以s=20+40t.当s=100时,100=20+40a,解得a=2.则大巴离营地的路程s与所用时间t 的函数表达式为s=20+40t,a的值为2.
(2)由函数图象可得,军车速度为60÷1=60( km/h),设部队官兵在仓库领取物资所用的时间为 xh,根据题意,得60(2-x)=100,解得
所以部队官兵在仓库领取物资所用的时间 h
7.【解】(1)由函数图象可以得出 A点在线段 BC上且AB=60 km,如图①所示.
(2)60;75
,所以M点的坐标为 ,0),M点的际意义是乙车到达A 地的时间 h
(4)150÷60=2.5(h),补全图象如图②.
当0≤x≤1时,y =60-60x;
当1
(5)设出发 xh时,甲、乙两车距A地的距离相等,由题意,得60x—60=75x—90 或60x—60=90—75x,解得.
所以出发2h h时,甲、乙两车距A地的距离相等
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
