华师大版七年级数学下册学案:6.1 从实际问题到方程(无答案)
文档属性
| 名称 | 华师大版七年级数学下册学案:6.1 从实际问题到方程(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 15.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-17 11:30:48 | ||
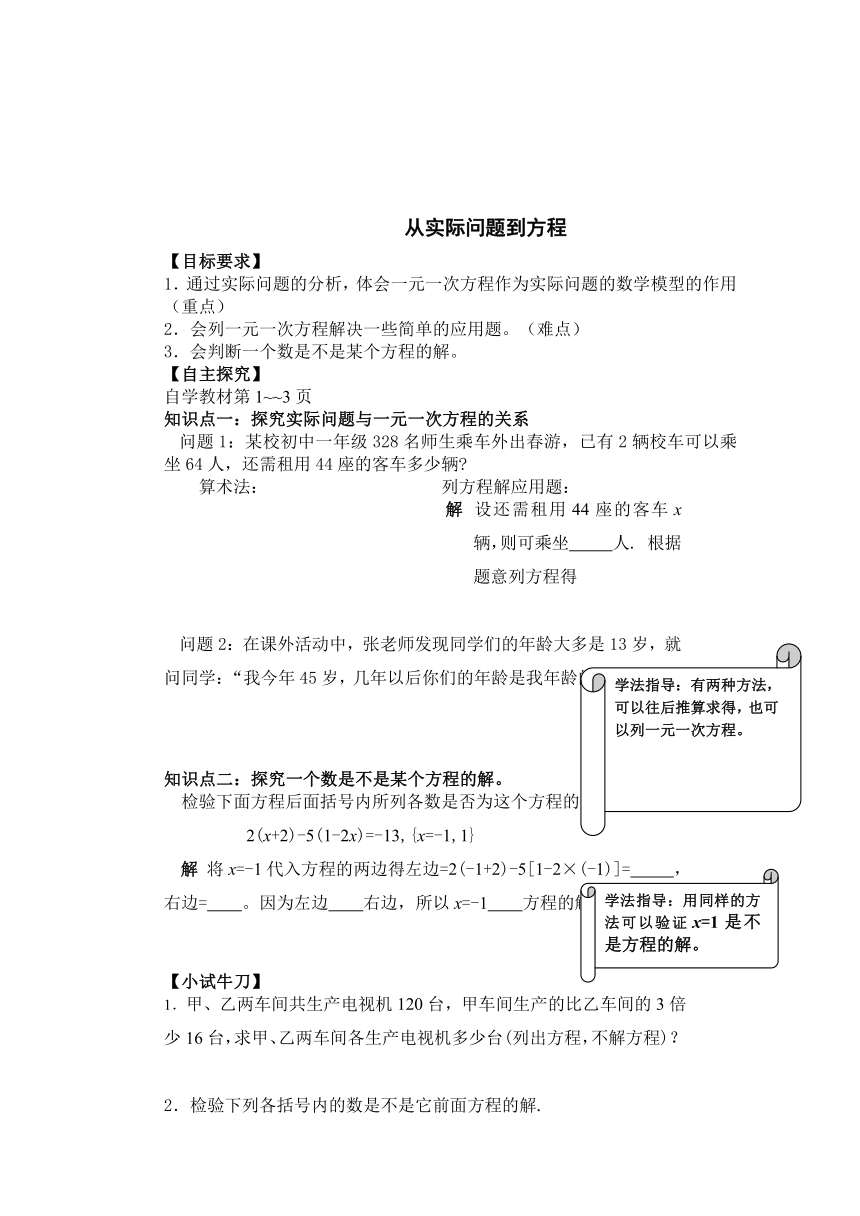
图片预览

文档简介
从实际问题到方程
【目标要求】
1.通过实际问题的分析,体会一元一次方程作为实际问题的数学模型的作用(重点)
2.会列一元一次方程解决一些简单的应用题。(难点)
3.会判断一个数是不是某个方程的解。
【自主探究】
自学教材第1~~3页
知识点一:探究实际问题与一元一次方程的关系
问题1:某校初中一年级328名师生乘车外出春游,已有2辆校车可以乘坐64人,还需租用44座的客车多少辆
算术法: 列方程解应用题:
解 设还需租用44座的客车x辆,则可乘坐 人. 根据题意列方程得
问题2:在课外活动中,张老师发现同学们的年龄大多是13岁,就问同学:“我今年45岁,几年以后你们的年龄是我年龄的三分之一 ”
知识点二:探究一个数是不是某个方程的解。
检验下面方程后面括号内所列各数是否为这个方程的解:
2(x+2)-5(1-2x)=-13,{x=-1,1}
解 将x=-1代入方程的两边得左边=2( ( http: / / www.21cnjy.com )-1+2)-5[1-2×(-1)]= , 右边= 。因为左边 右边,所以x=-1 方程的解.
【小试牛刀】
1.甲、乙两车间共生产电视机120台,甲车间生产的比乙车间的3倍少16台,求甲、乙两车间各生产电视机多少台(列出方程,不解方程)?
2.检验下列各括号内的数是不是它前面方程的解.
(1)x-3(x+2)=6+x (x=3,x=-4) (2) 2y(y-1)=3 (y=-1,y= )
【当堂反馈】
1.根据下列条件列方程:
(1)的5倍减去7等于它的3倍加上8;(2)甲比乙的2倍少3,甲乙两数的差为11;
(2)某数的2倍与的差等于这个数的加上6。
2.三捆树苗共670株,第一昆比第二捆多30株,第三捆比第二捆多40株,设第二捆有株,可列方程为___________.
3.检验下列各括号内的数是不是它前面方程的解.
5(x-1)(x-2)=0 (x=0,x=1,x=2)
【专题提升】
1.是方程的解,则的值是 ( )
(A)7; (B)1; (C)-1; (D)-7.
2.求作一个方程,使它的根为.
【整理评价与反思】
1 整理今天所学内容,展示 次,质疑 次,参与 次。
2 反思我这节课的表现,学习状态( )
A 很认真,值得表扬 B 还可以,继续努力 C 还得加油
【课后作业】
教科书第4页,习题6.1第1、3题.
学法指导:有两种方法,可以往后推算求得,也可以列一元一次方程。
学法指导:用同样的方法可以验证x=1是不是方程的解。
【目标要求】
1.通过实际问题的分析,体会一元一次方程作为实际问题的数学模型的作用(重点)
2.会列一元一次方程解决一些简单的应用题。(难点)
3.会判断一个数是不是某个方程的解。
【自主探究】
自学教材第1~~3页
知识点一:探究实际问题与一元一次方程的关系
问题1:某校初中一年级328名师生乘车外出春游,已有2辆校车可以乘坐64人,还需租用44座的客车多少辆
算术法: 列方程解应用题:
解 设还需租用44座的客车x辆,则可乘坐 人. 根据题意列方程得
问题2:在课外活动中,张老师发现同学们的年龄大多是13岁,就问同学:“我今年45岁,几年以后你们的年龄是我年龄的三分之一 ”
知识点二:探究一个数是不是某个方程的解。
检验下面方程后面括号内所列各数是否为这个方程的解:
2(x+2)-5(1-2x)=-13,{x=-1,1}
解 将x=-1代入方程的两边得左边=2( ( http: / / www.21cnjy.com )-1+2)-5[1-2×(-1)]= , 右边= 。因为左边 右边,所以x=-1 方程的解.
【小试牛刀】
1.甲、乙两车间共生产电视机120台,甲车间生产的比乙车间的3倍少16台,求甲、乙两车间各生产电视机多少台(列出方程,不解方程)?
2.检验下列各括号内的数是不是它前面方程的解.
(1)x-3(x+2)=6+x (x=3,x=-4) (2) 2y(y-1)=3 (y=-1,y= )
【当堂反馈】
1.根据下列条件列方程:
(1)的5倍减去7等于它的3倍加上8;(2)甲比乙的2倍少3,甲乙两数的差为11;
(2)某数的2倍与的差等于这个数的加上6。
2.三捆树苗共670株,第一昆比第二捆多30株,第三捆比第二捆多40株,设第二捆有株,可列方程为___________.
3.检验下列各括号内的数是不是它前面方程的解.
5(x-1)(x-2)=0 (x=0,x=1,x=2)
【专题提升】
1.是方程的解,则的值是 ( )
(A)7; (B)1; (C)-1; (D)-7.
2.求作一个方程,使它的根为.
【整理评价与反思】
1 整理今天所学内容,展示 次,质疑 次,参与 次。
2 反思我这节课的表现,学习状态( )
A 很认真,值得表扬 B 还可以,继续努力 C 还得加油
【课后作业】
教科书第4页,习题6.1第1、3题.
学法指导:有两种方法,可以往后推算求得,也可以列一元一次方程。
学法指导:用同样的方法可以验证x=1是不是方程的解。
