广东省广州市执信中学南沙学校2023—2024学年下学期阶段性考试(二) 数学试题(PDF版,无答案)
文档属性
| 名称 | 广东省广州市执信中学南沙学校2023—2024学年下学期阶段性考试(二) 数学试题(PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-29 18:05:13 | ||
图片预览

文档简介
2023 学年第二学期九年级阶段性练习(2)
一、单选题
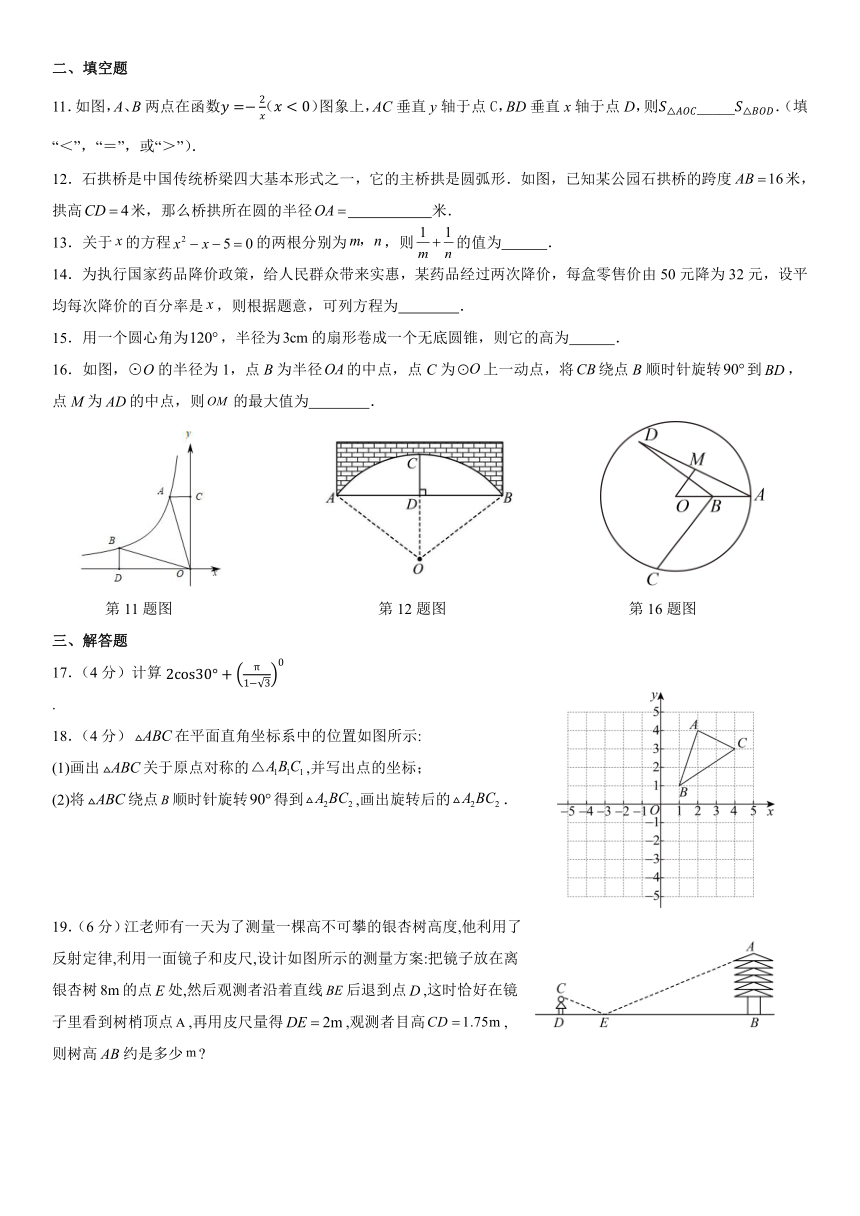
1.下列运动项目图标中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.一个不透明的盒子内装有 1个红球,1个黄球,1个蓝球,它们除颜色外其
次数 第 1次 第 2次 第 3次
余均相同.现从中随机摸出一球,记下颜色后放回搅匀,如此继续.如表是小
颜色 红球 红球
温前两次摸球的情况,当小温第三次摸球时,下列说法正确的是( )
A.一定摸到红球 B.一定摸不到红球
C.摸到黄球比摸到蓝球的可能性大 D.摸到红球、黄球和蓝球的可能性一样大
3 2.已知, a 2 b 1 0 ,则点 P a,b 关于原点对称的点的坐标是( )
A.(2,-1) B. 2, 1 C. 2,1 D. 2,1
4.已知 O的半径为 5,若 PO 4,则点 P与 O的位置关系是( )
A.点 P在 O内 B.点 P在 O上 C.点 P在 O外 D.无法判断
5.关于 x的一元二次方程 x2 2ax 1 0的根的情况是( )
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.实数根的个数与 a的取值有关
6.如图, AB是 O的直径,CD是 O的弦, CDB 32 ,则 ABC ( )
A.52 B.32 C.58 D.68
7.在Rt△ABC中, C 90 ,各边都扩大 2倍,则锐角 A的三角函数值( )
A 2 B C 1 D 1.扩大 倍 .不变 .缩小 2 .扩大 2
8.如图, CAD∽ CBA, AC : BC 1: 2,D为BC边上的一点.若 ACD的面积为 3,则△ABD
的面积为( )
A.6 B.8 C.9 D.12
9.如图, ABC中, ACB 90 , CAB 50 .将 ABC绕点 B逆时针旋转得到△A BC ,使
点C的对应点C 恰好落在边 AB上,则 CAA 的度数是( )
A.50 B.70 C.110 D.120
10 2.如图是二次函数 y ax bx c a 0 1图象的一部分,对称轴为 x ,且经过点 2,0 .下
2
5 5
列说法:①abc < 0;② 2b c 0;③ 4a 2b c 0;④若 , y1 , , y2 是抛物线上的两点,
2 2
则 y1 y
1
2;⑤ b m am b
1
(其中m ),其中说法正确的是( )
4 2
A.①②③ B.①②④ C.①②④⑤ D.②③④⑤
{#{QQABBDQywgAwgggAwggAoTBAACAB5hKCEE0wXWICokCskQAkQIAkjBJcCgCMCRYRgCGPgOBA4IoKAwIAZwFIAFFIA=B}A#A} =}#}
二、填空题
11 A B = 2.如图,、 两点在函数 ( < 0)图象上,AC垂直 y轴于点 C,BD垂直 x轴于点 D,则 △ _____ △ .(填
“<”,“=”,或“>”).
12.石拱桥是中国传统桥梁四大基本形式之一,它的主桥拱是圆弧形.如图,已知某公园石拱桥的跨度 AB 16米,
拱高CD 4米,那么桥拱所在圆的半径OA 米.
1 1
13.关于 x的方程 x2 x 5 0的两根分别为m,n,则 的值为 .
m n
14.为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每盒零售价由 50元降为 32元,设平
均每次降价的百分率是 x,则根据题意,可列方程为 .
15.用一个圆心角为120 ,半径为3cm的扇形卷成一个无底圆锥,则它的高为 .
16.如图,⊙O的半径为 1,点 B为半径OA的中点,点 C为 O上一动点,将CB绕点 B顺时针旋转90 到 BD,
点 M为 AD的中点,则OM 的最大值为 .
第 11题图 第 12题图 第 16题图
三、解答题
0
17.(4分)计算 2cos30° + π
1 3
.
18.(4分) ABC在平面直角坐标系中的位置如图所示:
(1)画出 ABC关于原点对称的△A1B1C1 ,并写出点的坐标;
(2)将 ABC绕点 B顺时针旋转90 得到 A2BC2 ,画出旋转后的 A2BC2 .
19.(6分)江老师有一天为了测量一棵高不可攀的银杏树高度,他利用了
反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离
银A杏B树 8m的点 E处,然后观测者沿着直线 BE后退到点D ,这时恰好在镜
子里看到树梢顶点A ,再用皮尺量得DE 2m ,观测者目高CD 1.75m ,
则树高 AB约是多少m
{#{QQABDBQywgAwgggAwggAoTBAACAB5hKCEE0wXWICokCskQAkQIAkjBJcCgCMCRYRgCGPgOBA4IoKAwIAZwFIAFFIA=B}A#A} =}#}
20.(6分)甲、乙两个口袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片所标有的三个数值分别
为 2,4, 6,乙袋中的三张卡片所标的数值为 2,3,5.
(1)小明在乙袋中随机抽取一张卡片,他抽出来的卡片上所标的数值是奇数的概率是 .
(2)小红先从甲袋中随机取出一张卡片,用 x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用 y表
示取出的卡片上的数值,把 x,y分别作为点 A的横坐标和纵坐标.请用列举法写出点 A x, y 的所有情况,并求点
A在第二象限的概率.
y k21.(8分)如图,反比例函数 和一次函数 y ax b的图象相交于点A和
x
点D,且点A的横坐标为1,点D的纵坐标为 1.过点A作 AB x轴于点 B,
AOB的面积为1.
(1)求反比例函数和一次函数的表达式;
k
(2)直接写出不等式 ax b的解集.
x
22.(10分)随着互联网应用的日趋成熟和完善,电子商务在近几年得到了迅猛的发展.某电商以每件 40元的价格
购进某款 T恤,以每件 60元的价格出售.经统计,“元旦”的前一周的销量为 500件,该电商在“元旦”期间进行降
价销售,经调查,发现该 T恤在“元旦”前一周销售量的基础上,每降价 1元,销售量就会增加 50件.设该 T恤降
价 x元,获得的利润为 w元.
(1)求 w与 x之间的函数关系式;
(2)若要求销售单价不低于成本,且按照物价部门规定销售利润率不高于30%,如何定价才能使得利润最大?并求出
利润
最大利润是多少元?(利润率 100%)
进价
{#{QQABDBQywgAwgggAwggAoTBAACAB5hKCEE0wXWICokCskQAkQIAkjBJcCgCMCRYRgCGPgOBA4IoKAwIAZwFIAFFIA=B}A#A} =}#}
23.(10分)【定义新知】定义:有一个角是其对角一半的圆内接四边形叫做圆美四边形,其中这个角叫做美角.
【初步应用】(1)如图 1,四边形 ABCD是圆美四边形, A是美角.
① A的度数为________ ;
②连接 BD,若 O的半径为 5,求线段 BD的长;
【拓展提升】
(2)如图 2,已知四边形 ABCD是圆美四边形, BAD是美角,连
接CA,若CA平分 BCD,若 O的半径为 6,,求 BC +CD的最大
值是多少?
24.(12分)已知抛物线G : y a(x 1)(x 3)与 x轴交于点 A,B(点 A在点 B的左侧),与 y轴交于点 C,点
P(0, t)( 1 t 2)为 y轴上一动点,过点 P作 y轴的垂线交抛物线 G于点 M、N(M与 N不重合).
(1)求点 C的纵坐标(用含 a的式子表示);
a 0 BC 15(2)当 时,若 ,求抛物线 G的纵坐标在 4a x 4a 5时的取值范围;
4
(3)对于 a(a 0)的每一个确定的值,MN 有最小值 m,若m 2,求 a的取值范围.
25.(12分)如图 1,等腰△ABC内接于 O,AB AC,连结OC,过点 B作 AC的垂线,交 O于点 D,交OC于
点 M,交 AC于点 E,连结 AD.
(1)若 D ,请用含 的代数式表示 OCA;
(2)如图 2.
①求证:CE 2 EM EB;
CE
②若 BM 5,DM 4,求 的值.
DE
x DM
S
(3) 3 CD y 四边形ABCD如图 ,连结 ,若 , ,求 y关于 x的函数表达式.
BM S△BEC
{#{QQABDBQywgAwgggAwggAoTBAACAB5hKCEE0wXWICokCskQAkQIAkjBJcCgCMCRYRgCGPgOBA4IoKAwIAZwFIAFFIA=B}A#A} =}#}
一、单选题
1.下列运动项目图标中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.一个不透明的盒子内装有 1个红球,1个黄球,1个蓝球,它们除颜色外其
次数 第 1次 第 2次 第 3次
余均相同.现从中随机摸出一球,记下颜色后放回搅匀,如此继续.如表是小
颜色 红球 红球
温前两次摸球的情况,当小温第三次摸球时,下列说法正确的是( )
A.一定摸到红球 B.一定摸不到红球
C.摸到黄球比摸到蓝球的可能性大 D.摸到红球、黄球和蓝球的可能性一样大
3 2.已知, a 2 b 1 0 ,则点 P a,b 关于原点对称的点的坐标是( )
A.(2,-1) B. 2, 1 C. 2,1 D. 2,1
4.已知 O的半径为 5,若 PO 4,则点 P与 O的位置关系是( )
A.点 P在 O内 B.点 P在 O上 C.点 P在 O外 D.无法判断
5.关于 x的一元二次方程 x2 2ax 1 0的根的情况是( )
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.实数根的个数与 a的取值有关
6.如图, AB是 O的直径,CD是 O的弦, CDB 32 ,则 ABC ( )
A.52 B.32 C.58 D.68
7.在Rt△ABC中, C 90 ,各边都扩大 2倍,则锐角 A的三角函数值( )
A 2 B C 1 D 1.扩大 倍 .不变 .缩小 2 .扩大 2
8.如图, CAD∽ CBA, AC : BC 1: 2,D为BC边上的一点.若 ACD的面积为 3,则△ABD
的面积为( )
A.6 B.8 C.9 D.12
9.如图, ABC中, ACB 90 , CAB 50 .将 ABC绕点 B逆时针旋转得到△A BC ,使
点C的对应点C 恰好落在边 AB上,则 CAA 的度数是( )
A.50 B.70 C.110 D.120
10 2.如图是二次函数 y ax bx c a 0 1图象的一部分,对称轴为 x ,且经过点 2,0 .下
2
5 5
列说法:①abc < 0;② 2b c 0;③ 4a 2b c 0;④若 , y1 , , y2 是抛物线上的两点,
2 2
则 y1 y
1
2;⑤ b m am b
1
(其中m ),其中说法正确的是( )
4 2
A.①②③ B.①②④ C.①②④⑤ D.②③④⑤
{#{QQABBDQywgAwgggAwggAoTBAACAB5hKCEE0wXWICokCskQAkQIAkjBJcCgCMCRYRgCGPgOBA4IoKAwIAZwFIAFFIA=B}A#A} =}#}
二、填空题
11 A B = 2.如图,、 两点在函数 ( < 0)图象上,AC垂直 y轴于点 C,BD垂直 x轴于点 D,则 △ _____ △ .(填
“<”,“=”,或“>”).
12.石拱桥是中国传统桥梁四大基本形式之一,它的主桥拱是圆弧形.如图,已知某公园石拱桥的跨度 AB 16米,
拱高CD 4米,那么桥拱所在圆的半径OA 米.
1 1
13.关于 x的方程 x2 x 5 0的两根分别为m,n,则 的值为 .
m n
14.为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每盒零售价由 50元降为 32元,设平
均每次降价的百分率是 x,则根据题意,可列方程为 .
15.用一个圆心角为120 ,半径为3cm的扇形卷成一个无底圆锥,则它的高为 .
16.如图,⊙O的半径为 1,点 B为半径OA的中点,点 C为 O上一动点,将CB绕点 B顺时针旋转90 到 BD,
点 M为 AD的中点,则OM 的最大值为 .
第 11题图 第 12题图 第 16题图
三、解答题
0
17.(4分)计算 2cos30° + π
1 3
.
18.(4分) ABC在平面直角坐标系中的位置如图所示:
(1)画出 ABC关于原点对称的△A1B1C1 ,并写出点的坐标;
(2)将 ABC绕点 B顺时针旋转90 得到 A2BC2 ,画出旋转后的 A2BC2 .
19.(6分)江老师有一天为了测量一棵高不可攀的银杏树高度,他利用了
反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离
银A杏B树 8m的点 E处,然后观测者沿着直线 BE后退到点D ,这时恰好在镜
子里看到树梢顶点A ,再用皮尺量得DE 2m ,观测者目高CD 1.75m ,
则树高 AB约是多少m
{#{QQABDBQywgAwgggAwggAoTBAACAB5hKCEE0wXWICokCskQAkQIAkjBJcCgCMCRYRgCGPgOBA4IoKAwIAZwFIAFFIA=B}A#A} =}#}
20.(6分)甲、乙两个口袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片所标有的三个数值分别
为 2,4, 6,乙袋中的三张卡片所标的数值为 2,3,5.
(1)小明在乙袋中随机抽取一张卡片,他抽出来的卡片上所标的数值是奇数的概率是 .
(2)小红先从甲袋中随机取出一张卡片,用 x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用 y表
示取出的卡片上的数值,把 x,y分别作为点 A的横坐标和纵坐标.请用列举法写出点 A x, y 的所有情况,并求点
A在第二象限的概率.
y k21.(8分)如图,反比例函数 和一次函数 y ax b的图象相交于点A和
x
点D,且点A的横坐标为1,点D的纵坐标为 1.过点A作 AB x轴于点 B,
AOB的面积为1.
(1)求反比例函数和一次函数的表达式;
k
(2)直接写出不等式 ax b的解集.
x
22.(10分)随着互联网应用的日趋成熟和完善,电子商务在近几年得到了迅猛的发展.某电商以每件 40元的价格
购进某款 T恤,以每件 60元的价格出售.经统计,“元旦”的前一周的销量为 500件,该电商在“元旦”期间进行降
价销售,经调查,发现该 T恤在“元旦”前一周销售量的基础上,每降价 1元,销售量就会增加 50件.设该 T恤降
价 x元,获得的利润为 w元.
(1)求 w与 x之间的函数关系式;
(2)若要求销售单价不低于成本,且按照物价部门规定销售利润率不高于30%,如何定价才能使得利润最大?并求出
利润
最大利润是多少元?(利润率 100%)
进价
{#{QQABDBQywgAwgggAwggAoTBAACAB5hKCEE0wXWICokCskQAkQIAkjBJcCgCMCRYRgCGPgOBA4IoKAwIAZwFIAFFIA=B}A#A} =}#}
23.(10分)【定义新知】定义:有一个角是其对角一半的圆内接四边形叫做圆美四边形,其中这个角叫做美角.
【初步应用】(1)如图 1,四边形 ABCD是圆美四边形, A是美角.
① A的度数为________ ;
②连接 BD,若 O的半径为 5,求线段 BD的长;
【拓展提升】
(2)如图 2,已知四边形 ABCD是圆美四边形, BAD是美角,连
接CA,若CA平分 BCD,若 O的半径为 6,,求 BC +CD的最大
值是多少?
24.(12分)已知抛物线G : y a(x 1)(x 3)与 x轴交于点 A,B(点 A在点 B的左侧),与 y轴交于点 C,点
P(0, t)( 1 t 2)为 y轴上一动点,过点 P作 y轴的垂线交抛物线 G于点 M、N(M与 N不重合).
(1)求点 C的纵坐标(用含 a的式子表示);
a 0 BC 15(2)当 时,若 ,求抛物线 G的纵坐标在 4a x 4a 5时的取值范围;
4
(3)对于 a(a 0)的每一个确定的值,MN 有最小值 m,若m 2,求 a的取值范围.
25.(12分)如图 1,等腰△ABC内接于 O,AB AC,连结OC,过点 B作 AC的垂线,交 O于点 D,交OC于
点 M,交 AC于点 E,连结 AD.
(1)若 D ,请用含 的代数式表示 OCA;
(2)如图 2.
①求证:CE 2 EM EB;
CE
②若 BM 5,DM 4,求 的值.
DE
x DM
S
(3) 3 CD y 四边形ABCD如图 ,连结 ,若 , ,求 y关于 x的函数表达式.
BM S△BEC
{#{QQABDBQywgAwgggAwggAoTBAACAB5hKCEE0wXWICokCskQAkQIAkjBJcCgCMCRYRgCGPgOBA4IoKAwIAZwFIAFFIA=B}A#A} =}#}
同课章节目录
