11.1.1 平面内点的坐标 第1课时 平面直角坐标系 课件(共28张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 11.1.1 平面内点的坐标 第1课时 平面直角坐标系 课件(共28张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-30 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
沪科版
11.1.1 平面直角坐标系
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 理解平面直角坐标系以及横轴、纵轴、原点、坐标平面等概念;
2. 理解四象限及各象限、原点、坐标轴上点的坐标特征;
3.会用象限或坐标轴说明直角坐标系内点的位置,能根据点的位置确定横、纵坐标的符号.
4.能在实际情境中建立合适的平面直角坐标系,并表示出正确位置
学习目标
重点
难点
问题1 如图是某教室学生座位的平面图,你能描述吴小明和王健同学座位的位置吗?
1 2 3 4 5 6 7 8
6
5
4
3
2
1
吴小明
王健
行
列
讲 台
第5行第2列
第3行第5列
新课引入
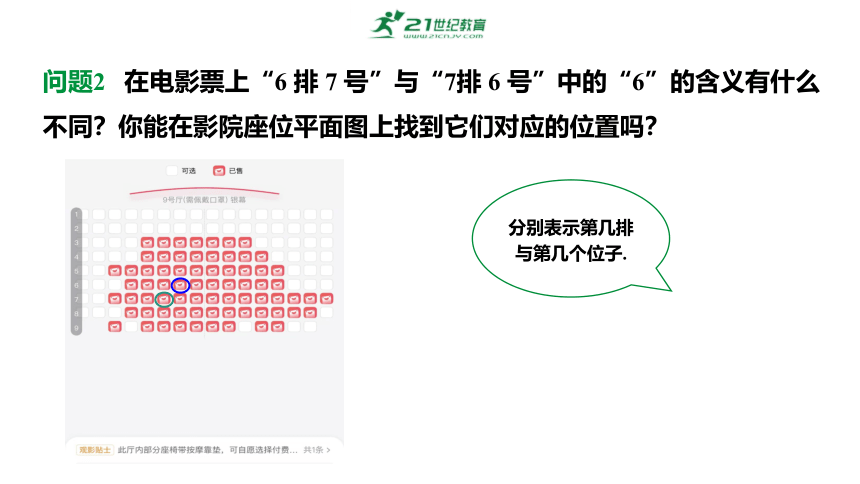
问题2 在电影票上“6 排 7 号”与“7排 6 号”中的“6”的含义有什么不同?你能在影院座位平面图上找到它们对应的位置吗?
分别表示第几排与第几个位子.
想一想在上边两个例子中,在平面内,确定一个位置需要几个数据?
需要两个数据!
你还能想到日常生活中其他类似的例子吗?
在平面内,确定一个位置还有什么方法?让我们继续探究.
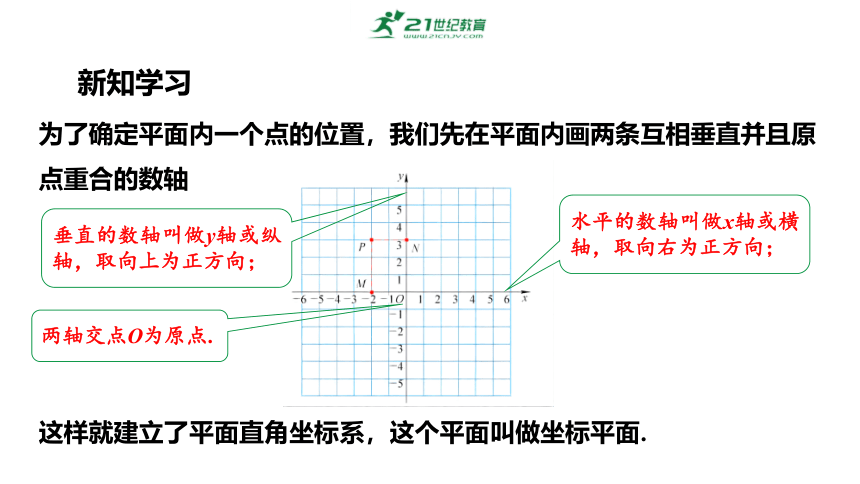
为了确定平面内一个点的位置,我们先在平面内画两条互相垂直并且原点重合的数轴
这样就建立了平面直角坐标系,这个平面叫做坐标平面.
水平的数轴叫做x轴或横轴,取向右为正方向;
垂直的数轴叫做y轴或纵轴,取向上为正方向;
两轴交点О为原点.
新知学习
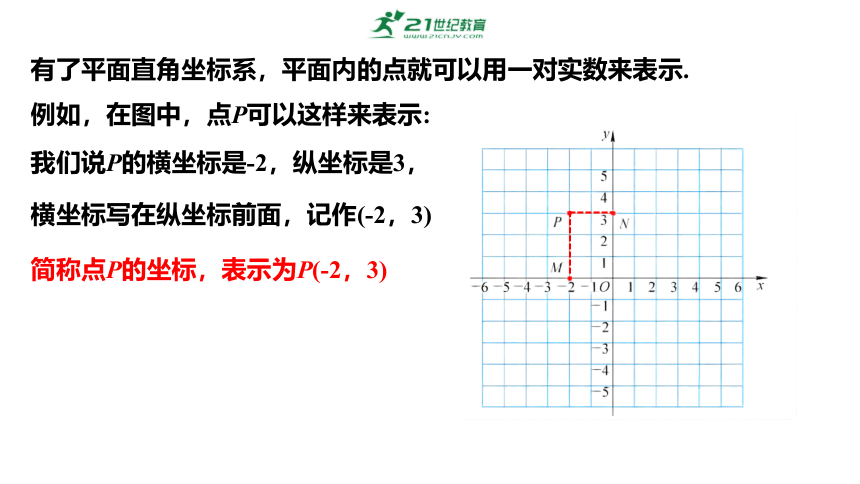
有了平面直角坐标系,平面内的点就可以用一对实数来表示.
例如,在图中,点P可以这样来表示:
横坐标写在纵坐标前面,记作(-2,3)
我们说P的横坐标是-2,纵坐标是3,
简称点P的坐标,表示为P(-2,3)
操作
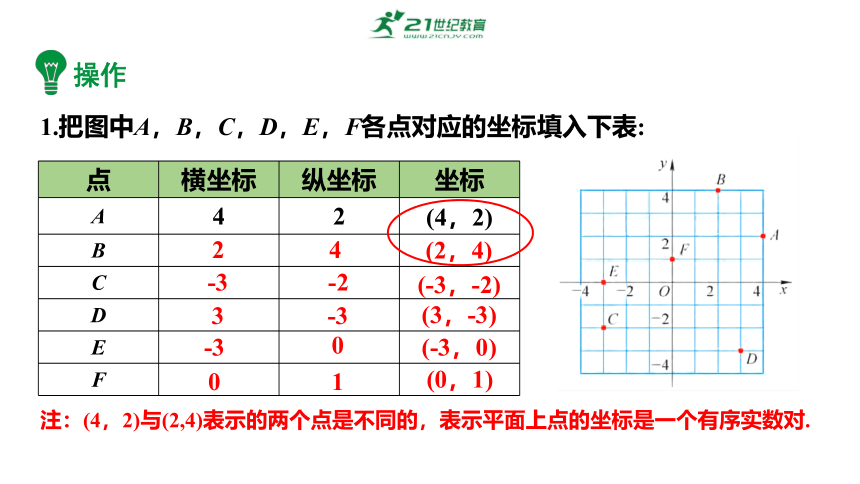
1.把图中A,B,C,D,E,F各点对应的坐标填入下表:
点 横坐标 纵坐标 坐标
A 4 2 (4,2)
B
C
D
E
F
注:(4,2)与(2,4)表示的两个点是不同的,表示平面上点的坐标是一个有序实数对.
2
4
(2,4)
-3
-2
(-3,-2)
3
-3
(3,-3)
-3
0
(-3,0)
0
1
(0,1)
2.在平面直角坐标系中,描出下列各点:
A(3,4),B(3,-2) ,C(1,2),D(-2,2),E(2,0),F(0,-3).
A
B
C
D
E
F
1.两点连线平行于横轴(x轴),两点纵坐标相同;
2.两点连线平行于纵轴(y轴),两点横坐标相同;
点A和点B坐标有什么特征?
点C和点D坐标有什么特征?
A(3,4),B(3,-2) ,C(1,2),D(-2,2),E(2,0),F(0,-3).
A
B
C
D
E
F
1.横轴(x轴)上的点,纵坐标为0;
2.纵轴(y轴)上的点,横坐标为0.
点E和点F坐标有什么特征?
1.两点连线平行于横轴(x轴),两点纵坐标相同;
2.两点连线平行于纵轴(y轴),两点横坐标相同;
3.横轴上的点,纵坐标为0;
4.纵轴上的点,横坐标为0.
归纳
A(3,4),B(3,-2) ,C(1,2),D(-2,2),E(2,0),F(0,-3).
A
B
C
D
E
F
点A到x轴的距离=4;
点A到y轴的距离=3.
点A到x轴和到y轴的距离分别是多少?
同样地,点D到x轴和y轴的距离分别是多少?
延伸
归纳
点到坐标轴的距离:点 P(a,b)到 x 轴的距离是| b | ,到y轴的距离是| a | .
1.在图中,所画的平面直角坐标系正确的是( )
D
没有原点O
x轴与y轴不垂直
水平的数轴叫x轴
针对训练
2.如图,点A的坐标为( )
A. ( -2,3)
B. ( 2,-3)
C . ( -2,-3)
D . ( 2,3)
A
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
3.在如图所示的平面直角坐标系中,有A,B,C,D,E,F六个点,试写出这六个点的坐标.
A(3,1)
B(-4,3)
C(-2,-2)
D(2,-3)
E(4,0)
F(0,2)
4. 已知 P ( 3 , -2 ),则 P 点到 x 轴的距离为_______,到 y 轴的距离为_______.
2
3
刚认识了平面直角坐标系中点的表示,我们继续探究坐标平面的特征
x轴和y轴把坐标平面分成四个部分
分别叫做第一、二、三、四象限
第一象限
(+,+)
第二象限
(-,+)
第三象限
(+,-)
第四象限
(-,-)
注:坐标轴上的点,也就是x轴,y轴上的点不属于任何一个象限
观察坐标系,填写各象限内的点的坐标的特征:
点 点所在 象限 横坐标的符号 纵坐标
的符号
A
B
C
D
E
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
操作
-
第一象限
第二象限
第三象限
第四象限
y轴负半轴
通过直角坐标系的建立,我们把平面内的点与有序实数对一一对应起来.即对于坐标平面内任意一点P,都有唯一的一个有序实数对(x,y)和它对应;反之,对于任意一个有序实数对(x,y),在坐标平面内都有唯一的一点Р和它对应.
点
有序实数对
一一对应
1.右图是某学校的平面示意图,图中小正方形的边长为单位长度.
请建立合适的平面直角坐标系.
(1)写出教学楼、实验楼、图书馆的坐标;
(2)学校准备在(3,1)处建一栋学生公寓,请你标出学生公寓的位置.
(1)教学楼(2,4)、实验楼(3,-4)、图书馆(-4,3).
·
(3,1)
O
1 2 3 4 5 6
-5 -4 -3 -2 -1
1
2
3
4
5
-5
-4
-3
-2
-1
x
y
针对训练
(2)学生公寓位置如图所示.
A(3,6) B(0,-8)
C(-7,-5) D(-6,0)
E(-3.6,5) F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y 轴负半轴上
x 轴负半轴上
原点
2.下列各点分别在坐标平面的什么位置上?
3.已知王东同学家在学校东100m、北150m处,赵西同学的家在学校西200m、南50m处.如图,把学校所在地取作原点,建立平面直角坐标系,试在坐标系中画出王东、赵西同学家的位置并用坐标表示它们(每一单位长度代表50m).
王东家
(200、50)
(100,150)
赵西家
学校
1.如图,象棋盘上,若“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点( ).
x
y
O
1
2
3
-1
-2
-1
-2
1
2
-2,1
随堂练习
2.点 M ( x , y )在第四象限且 x2 = 9,y2 = 16,则 M 点的坐标为_______.
( 3 , -4 )
3.已知a<b<0,那么点P(a-b,-b)在第几象限?
-
-
在第三象限
4.“桃花源”的入口很隐蔽,探险者在地图上建立了一个平面直角坐标系,巧妙地运用坐标来确定它所在的位置.他首先确定了四课桃花树的位置:
A(-1,2),B(-1,-4),C(5,-4),D(5,2).
发现AC与BD的交点E处就是“桃花源的入口”.试指出“桃花源”入口E的坐标.
A
B
C
D
E(2,-1)
入口E的坐标为(2,-1).
平面直角
坐标系
x 轴和 y 轴把坐标平面分成四个部分,分别叫做第一、
二、三、四象限;
坐标平面内点的坐标特征;
点与有序实数对的对应关系:
平面直角坐
标系内点的
坐标特征
平面直角
坐标系
水平的数轴叫做x 轴或横轴,取向右为正方向
垂直的数轴叫做y 轴或纵轴,取向上为正方向
两轴交点 O 为原点
点
有序实数对
一一对应
课堂小结
沪科版
11.1.1 平面直角坐标系
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 理解平面直角坐标系以及横轴、纵轴、原点、坐标平面等概念;
2. 理解四象限及各象限、原点、坐标轴上点的坐标特征;
3.会用象限或坐标轴说明直角坐标系内点的位置,能根据点的位置确定横、纵坐标的符号.
4.能在实际情境中建立合适的平面直角坐标系,并表示出正确位置
学习目标
重点
难点
问题1 如图是某教室学生座位的平面图,你能描述吴小明和王健同学座位的位置吗?
1 2 3 4 5 6 7 8
6
5
4
3
2
1
吴小明
王健
行
列
讲 台
第5行第2列
第3行第5列
新课引入
问题2 在电影票上“6 排 7 号”与“7排 6 号”中的“6”的含义有什么不同?你能在影院座位平面图上找到它们对应的位置吗?
分别表示第几排与第几个位子.
想一想在上边两个例子中,在平面内,确定一个位置需要几个数据?
需要两个数据!
你还能想到日常生活中其他类似的例子吗?
在平面内,确定一个位置还有什么方法?让我们继续探究.
为了确定平面内一个点的位置,我们先在平面内画两条互相垂直并且原点重合的数轴
这样就建立了平面直角坐标系,这个平面叫做坐标平面.
水平的数轴叫做x轴或横轴,取向右为正方向;
垂直的数轴叫做y轴或纵轴,取向上为正方向;
两轴交点О为原点.
新知学习
有了平面直角坐标系,平面内的点就可以用一对实数来表示.
例如,在图中,点P可以这样来表示:
横坐标写在纵坐标前面,记作(-2,3)
我们说P的横坐标是-2,纵坐标是3,
简称点P的坐标,表示为P(-2,3)
操作
1.把图中A,B,C,D,E,F各点对应的坐标填入下表:
点 横坐标 纵坐标 坐标
A 4 2 (4,2)
B
C
D
E
F
注:(4,2)与(2,4)表示的两个点是不同的,表示平面上点的坐标是一个有序实数对.
2
4
(2,4)
-3
-2
(-3,-2)
3
-3
(3,-3)
-3
0
(-3,0)
0
1
(0,1)
2.在平面直角坐标系中,描出下列各点:
A(3,4),B(3,-2) ,C(1,2),D(-2,2),E(2,0),F(0,-3).
A
B
C
D
E
F
1.两点连线平行于横轴(x轴),两点纵坐标相同;
2.两点连线平行于纵轴(y轴),两点横坐标相同;
点A和点B坐标有什么特征?
点C和点D坐标有什么特征?
A(3,4),B(3,-2) ,C(1,2),D(-2,2),E(2,0),F(0,-3).
A
B
C
D
E
F
1.横轴(x轴)上的点,纵坐标为0;
2.纵轴(y轴)上的点,横坐标为0.
点E和点F坐标有什么特征?
1.两点连线平行于横轴(x轴),两点纵坐标相同;
2.两点连线平行于纵轴(y轴),两点横坐标相同;
3.横轴上的点,纵坐标为0;
4.纵轴上的点,横坐标为0.
归纳
A(3,4),B(3,-2) ,C(1,2),D(-2,2),E(2,0),F(0,-3).
A
B
C
D
E
F
点A到x轴的距离=4;
点A到y轴的距离=3.
点A到x轴和到y轴的距离分别是多少?
同样地,点D到x轴和y轴的距离分别是多少?
延伸
归纳
点到坐标轴的距离:点 P(a,b)到 x 轴的距离是| b | ,到y轴的距离是| a | .
1.在图中,所画的平面直角坐标系正确的是( )
D
没有原点O
x轴与y轴不垂直
水平的数轴叫x轴
针对训练
2.如图,点A的坐标为( )
A. ( -2,3)
B. ( 2,-3)
C . ( -2,-3)
D . ( 2,3)
A
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
3.在如图所示的平面直角坐标系中,有A,B,C,D,E,F六个点,试写出这六个点的坐标.
A(3,1)
B(-4,3)
C(-2,-2)
D(2,-3)
E(4,0)
F(0,2)
4. 已知 P ( 3 , -2 ),则 P 点到 x 轴的距离为_______,到 y 轴的距离为_______.
2
3
刚认识了平面直角坐标系中点的表示,我们继续探究坐标平面的特征
x轴和y轴把坐标平面分成四个部分
分别叫做第一、二、三、四象限
第一象限
(+,+)
第二象限
(-,+)
第三象限
(+,-)
第四象限
(-,-)
注:坐标轴上的点,也就是x轴,y轴上的点不属于任何一个象限
观察坐标系,填写各象限内的点的坐标的特征:
点 点所在 象限 横坐标的符号 纵坐标
的符号
A
B
C
D
E
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
操作
-
第一象限
第二象限
第三象限
第四象限
y轴负半轴
通过直角坐标系的建立,我们把平面内的点与有序实数对一一对应起来.即对于坐标平面内任意一点P,都有唯一的一个有序实数对(x,y)和它对应;反之,对于任意一个有序实数对(x,y),在坐标平面内都有唯一的一点Р和它对应.
点
有序实数对
一一对应
1.右图是某学校的平面示意图,图中小正方形的边长为单位长度.
请建立合适的平面直角坐标系.
(1)写出教学楼、实验楼、图书馆的坐标;
(2)学校准备在(3,1)处建一栋学生公寓,请你标出学生公寓的位置.
(1)教学楼(2,4)、实验楼(3,-4)、图书馆(-4,3).
·
(3,1)
O
1 2 3 4 5 6
-5 -4 -3 -2 -1
1
2
3
4
5
-5
-4
-3
-2
-1
x
y
针对训练
(2)学生公寓位置如图所示.
A(3,6) B(0,-8)
C(-7,-5) D(-6,0)
E(-3.6,5) F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y 轴负半轴上
x 轴负半轴上
原点
2.下列各点分别在坐标平面的什么位置上?
3.已知王东同学家在学校东100m、北150m处,赵西同学的家在学校西200m、南50m处.如图,把学校所在地取作原点,建立平面直角坐标系,试在坐标系中画出王东、赵西同学家的位置并用坐标表示它们(每一单位长度代表50m).
王东家
(200、50)
(100,150)
赵西家
学校
1.如图,象棋盘上,若“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点( ).
x
y
O
1
2
3
-1
-2
-1
-2
1
2
-2,1
随堂练习
2.点 M ( x , y )在第四象限且 x2 = 9,y2 = 16,则 M 点的坐标为_______.
( 3 , -4 )
3.已知a<b<0,那么点P(a-b,-b)在第几象限?
-
-
在第三象限
4.“桃花源”的入口很隐蔽,探险者在地图上建立了一个平面直角坐标系,巧妙地运用坐标来确定它所在的位置.他首先确定了四课桃花树的位置:
A(-1,2),B(-1,-4),C(5,-4),D(5,2).
发现AC与BD的交点E处就是“桃花源的入口”.试指出“桃花源”入口E的坐标.
A
B
C
D
E(2,-1)
入口E的坐标为(2,-1).
平面直角
坐标系
x 轴和 y 轴把坐标平面分成四个部分,分别叫做第一、
二、三、四象限;
坐标平面内点的坐标特征;
点与有序实数对的对应关系:
平面直角坐
标系内点的
坐标特征
平面直角
坐标系
水平的数轴叫做x 轴或横轴,取向右为正方向
垂直的数轴叫做y 轴或纵轴,取向上为正方向
两轴交点 O 为原点
点
有序实数对
一一对应
课堂小结
