11.1.2 平面内点的坐标 第2课时 平面直角坐标系与图形的结合 课件(共20张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 11.1.2 平面内点的坐标 第2课时 平面直角坐标系与图形的结合 课件(共20张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 369.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-30 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
八年级上
沪科版
11.1.2 平面直角坐标系
与图形的结合
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.在给定的直角坐标系中,会根据坐标描出点的位置,并能求出顺次连接所得图形的面积;
2. 能建立适当的直角坐标系,描述图形的位置;
3.通过用直角坐标系表示图形的位置,使学生体会平面直角坐标系在实际生活中的应用.
学习目标
重点
难点
上节课学面直角坐标系的概念,点在平面直角坐标系中的表示及象限
判断正误
1.点A(-3,-2)在第三象限 ( )
2.点B(-2,0)在第二象限 ( )
3.第四象限内点横坐标、纵坐标符号分别是-、+ ( )
知识回顾
某小区里有一块如图所示的空地,打算进行绿化,小明想请他的同学小慧提一些建议,小明要在电话中告诉小慧同学如图所示的图形,为了描述清楚,他使用了直角坐标系的知识.你知道小明是怎样叙述的吗?
新课引入
x
y
A(8,0)
B(8,2)
C(3,2)
D(3,5)
E(0,5)
会在坐标系中表示点了,你会表示线段,图形吗?
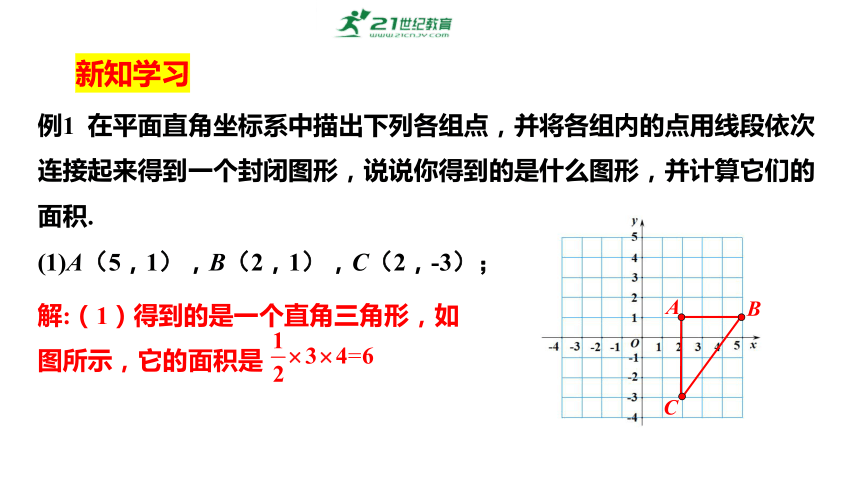
例1 在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来得到一个封闭图形,说说你得到的是什么图形,并计算它们的面积.
(1)A(5,1),B(2,1),C(2,-3);
新知学习
解:(1)得到的是一个直角三角形,如图所示,它的面积是
A
B
C
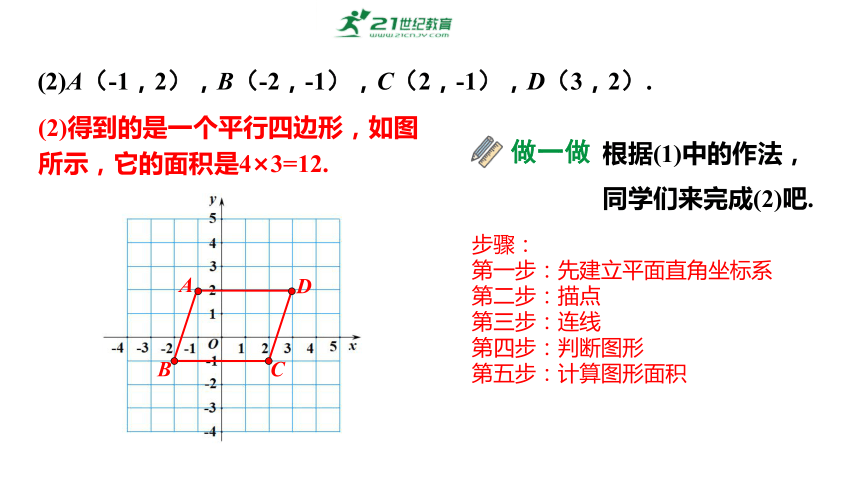
(2)A(-1,2),B(-2,-1),C(2,-1),D(3,2).
做一做
根据(1)中的作法,
同学们来完成(2)吧.
步骤:
第一步:先建立平面直角坐标系
第二步:描点
第三步:连线
第四步:判断图形
第五步:计算图形面积
(2)得到的是一个平行四边形,如图所示,它的面积是4×3=12.
A
B
C
D
交流
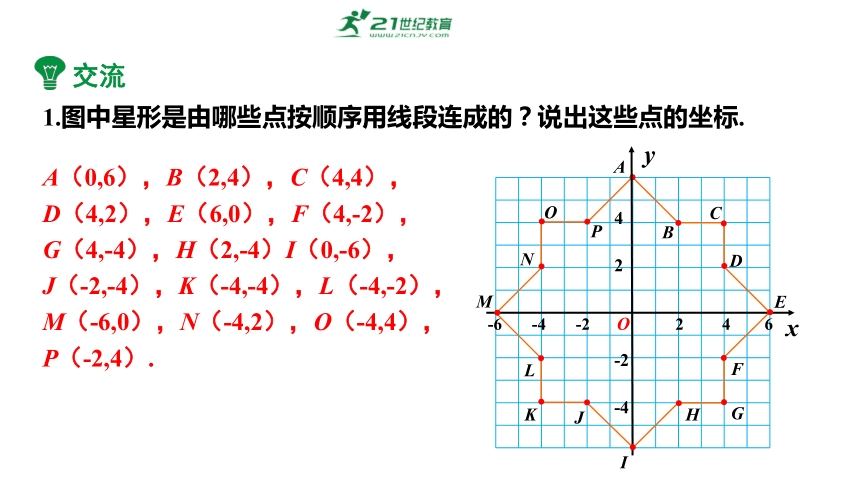
1.图中星形是由哪些点按顺序用线段连成的?说出这些点的坐标.
x
-6 -4 -2 2 4 6
O
A
B
C
D
E
F
G
H
J
K
L
M
N
O
P
A(0,6),B(2,4),C(4,4),
D(4,2),E(6,0),F(4,-2),
G(4,-4),H(2,-4)I(0,-6),
J(-2,-4),K(-4,-4),L(-4,-2),
M(-6,0),N(-4,2),O(-4,4),P(-2,4).
y
4
2
-2
-4
I
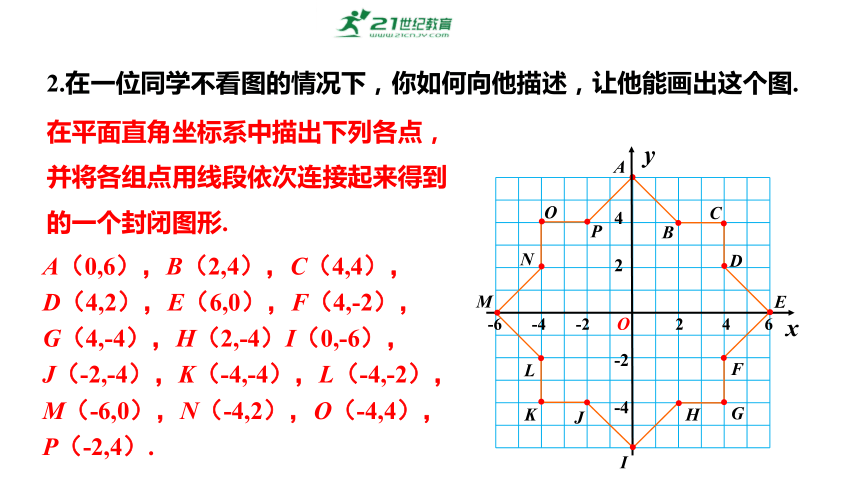
2.在一位同学不看图的情况下,你如何向他描述,让他能画出这个图.
在平面直角坐标系中描出下列各点,并将各组点用线段依次连接起来得到的一个封闭图形.
x
-6 -4 -2 2 4 6
O
A
B
C
D
E
F
G
H
J
K
L
M
N
O
P
y
4
2
-2
-4
A(0,6),B(2,4),C(4,4),
D(4,2),E(6,0),F(4,-2),
G(4,-4),H(2,-4)I(0,-6),
J(-2,-4),K(-4,-4),L(-4,-2),
M(-6,0),N(-4,2),O(-4,4),P(-2,4).
I
例2 如图,正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系的坐标.
A
B
C
D
解:如图,以顶点A为原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系.
A(0,0),B(4,0),
C(4,4),D(0,4).
-2 2 4 6
x
6
4
2
-2
y
O
你能另建一个平面直角坐标系,并写出此时顶点A,B,C,D的坐标吗?
A
B
C
D
O
-4 -2 2 4
x
4
2
-2
-4
y
A(-2,-2),B(2,-2),
C(2,2),D(-2,2).
做一做
1.(1)如图,在平面直角坐标系中描出下列各点:
A(2,0),B(1,3),C(-2,-2),D(1,-2)
(2)按次序A→B→C→D→A将所描出的点用线段连接起来,看看得到的是什么图形.
(3)计算所得到的图形面积.
针对训练
A
B
C
D
(2)得到的是两个三角形,△ABD和△BCD.
(3)S△ABD= ×5×1= ,
S△BCD= ×3×5= ,
图形面积=S△ABD+S△BCD = + =10.
解:(1)描出下列各点如图所示;
2.假如你想让你的同学在不看图的情况下,准确地画出如图所示的“小船”图案,你怎样来描述它?
解:小船是由平面直角坐标系中以下点顺次连接得到的封闭型图案:
A(-3,0),B(-2,-1),C(3,-1),D(4,0),E(2,0),B(0,4)
G(0,2),H(-2,0)
1. 已知 A( 1 , 4 ),B( -4 , 0 ),C( 2 , 0 ),求 S△ABC .
A( 1 , 4 )
B( -4 , 0 )
C( 2 , 0 )
解:∵B ( -4 , 0 ),C ( 2 , 0 ),
∴BC = 6.
∵ A ( 1 , 4 )
∴BC 边上的高是 4.
即 S△ABC = ×6×4 = 12
求坐标平面内图形面积:
①直接法,计算三角形一边的长,并求出该边上的高。
随堂练习
若点 B、点 C 的坐标不变,△ABC 的面积为 12,点 A 的横坐标为 1,求点 A 的坐标.
A( 1 , 4 )
B( -4 , 0 )
C( 2 , 0 )
解:A 点坐标为( 1 , 4 ) 或 ( 1 , -4 )
A( 1 , -4 )
变式
2. 已知A,B两点的坐标如图所示,求△AOB的面积.
求坐标平面内图形面积:
②补形法,将面积转化成若干个特殊的四边形和三角形的面积的和与差。
解:过B点作x轴的垂线,垂足为M,过A点作y轴的垂线,垂足为N,两垂线交于点G,则四边形OMGN是矩形,由A,B点的坐标可知:OM=4,ON=5,AN=2,AG=2,BM=2,BG=3.
S△AOB=S矩形OMGN-S△ANO-S△AGB-S△BOM=8
你还有其他方法求△AOB的面积吗?
思考
3.求出如图所示的图形的面积
解:将图形分割成如图所示的三角形
和矩形.
S=S矩形+S三角形=24+12=36
求坐标平面内图形面积:
③分割法,将不规则图形分割成便于计算面积的三角形或四边形。
1. 如何建立平面直角坐标系?
答:选择点作为原点;
过原点在两个互相垂直的方向上分别作出 x 轴和 y 轴;
标出正方向和单位长度.
课堂小结
2. 如何计算坐标平面内图形面积?
方法一:直接法,计算三角形一边的长,并求出该边上的高;
方法二:补形法,将面积转化成若干个特殊的四边形和三角形的面积的和与差;
方法三:分割法,选择一条恰当的直线,将不规则的图形分割成两个便于计算面积的图形.
八年级上
沪科版
11.1.2 平面直角坐标系
与图形的结合
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.在给定的直角坐标系中,会根据坐标描出点的位置,并能求出顺次连接所得图形的面积;
2. 能建立适当的直角坐标系,描述图形的位置;
3.通过用直角坐标系表示图形的位置,使学生体会平面直角坐标系在实际生活中的应用.
学习目标
重点
难点
上节课学面直角坐标系的概念,点在平面直角坐标系中的表示及象限
判断正误
1.点A(-3,-2)在第三象限 ( )
2.点B(-2,0)在第二象限 ( )
3.第四象限内点横坐标、纵坐标符号分别是-、+ ( )
知识回顾
某小区里有一块如图所示的空地,打算进行绿化,小明想请他的同学小慧提一些建议,小明要在电话中告诉小慧同学如图所示的图形,为了描述清楚,他使用了直角坐标系的知识.你知道小明是怎样叙述的吗?
新课引入
x
y
A(8,0)
B(8,2)
C(3,2)
D(3,5)
E(0,5)
会在坐标系中表示点了,你会表示线段,图形吗?
例1 在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来得到一个封闭图形,说说你得到的是什么图形,并计算它们的面积.
(1)A(5,1),B(2,1),C(2,-3);
新知学习
解:(1)得到的是一个直角三角形,如图所示,它的面积是
A
B
C
(2)A(-1,2),B(-2,-1),C(2,-1),D(3,2).
做一做
根据(1)中的作法,
同学们来完成(2)吧.
步骤:
第一步:先建立平面直角坐标系
第二步:描点
第三步:连线
第四步:判断图形
第五步:计算图形面积
(2)得到的是一个平行四边形,如图所示,它的面积是4×3=12.
A
B
C
D
交流
1.图中星形是由哪些点按顺序用线段连成的?说出这些点的坐标.
x
-6 -4 -2 2 4 6
O
A
B
C
D
E
F
G
H
J
K
L
M
N
O
P
A(0,6),B(2,4),C(4,4),
D(4,2),E(6,0),F(4,-2),
G(4,-4),H(2,-4)I(0,-6),
J(-2,-4),K(-4,-4),L(-4,-2),
M(-6,0),N(-4,2),O(-4,4),P(-2,4).
y
4
2
-2
-4
I
2.在一位同学不看图的情况下,你如何向他描述,让他能画出这个图.
在平面直角坐标系中描出下列各点,并将各组点用线段依次连接起来得到的一个封闭图形.
x
-6 -4 -2 2 4 6
O
A
B
C
D
E
F
G
H
J
K
L
M
N
O
P
y
4
2
-2
-4
A(0,6),B(2,4),C(4,4),
D(4,2),E(6,0),F(4,-2),
G(4,-4),H(2,-4)I(0,-6),
J(-2,-4),K(-4,-4),L(-4,-2),
M(-6,0),N(-4,2),O(-4,4),P(-2,4).
I
例2 如图,正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系的坐标.
A
B
C
D
解:如图,以顶点A为原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系.
A(0,0),B(4,0),
C(4,4),D(0,4).
-2 2 4 6
x
6
4
2
-2
y
O
你能另建一个平面直角坐标系,并写出此时顶点A,B,C,D的坐标吗?
A
B
C
D
O
-4 -2 2 4
x
4
2
-2
-4
y
A(-2,-2),B(2,-2),
C(2,2),D(-2,2).
做一做
1.(1)如图,在平面直角坐标系中描出下列各点:
A(2,0),B(1,3),C(-2,-2),D(1,-2)
(2)按次序A→B→C→D→A将所描出的点用线段连接起来,看看得到的是什么图形.
(3)计算所得到的图形面积.
针对训练
A
B
C
D
(2)得到的是两个三角形,△ABD和△BCD.
(3)S△ABD= ×5×1= ,
S△BCD= ×3×5= ,
图形面积=S△ABD+S△BCD = + =10.
解:(1)描出下列各点如图所示;
2.假如你想让你的同学在不看图的情况下,准确地画出如图所示的“小船”图案,你怎样来描述它?
解:小船是由平面直角坐标系中以下点顺次连接得到的封闭型图案:
A(-3,0),B(-2,-1),C(3,-1),D(4,0),E(2,0),B(0,4)
G(0,2),H(-2,0)
1. 已知 A( 1 , 4 ),B( -4 , 0 ),C( 2 , 0 ),求 S△ABC .
A( 1 , 4 )
B( -4 , 0 )
C( 2 , 0 )
解:∵B ( -4 , 0 ),C ( 2 , 0 ),
∴BC = 6.
∵ A ( 1 , 4 )
∴BC 边上的高是 4.
即 S△ABC = ×6×4 = 12
求坐标平面内图形面积:
①直接法,计算三角形一边的长,并求出该边上的高。
随堂练习
若点 B、点 C 的坐标不变,△ABC 的面积为 12,点 A 的横坐标为 1,求点 A 的坐标.
A( 1 , 4 )
B( -4 , 0 )
C( 2 , 0 )
解:A 点坐标为( 1 , 4 ) 或 ( 1 , -4 )
A( 1 , -4 )
变式
2. 已知A,B两点的坐标如图所示,求△AOB的面积.
求坐标平面内图形面积:
②补形法,将面积转化成若干个特殊的四边形和三角形的面积的和与差。
解:过B点作x轴的垂线,垂足为M,过A点作y轴的垂线,垂足为N,两垂线交于点G,则四边形OMGN是矩形,由A,B点的坐标可知:OM=4,ON=5,AN=2,AG=2,BM=2,BG=3.
S△AOB=S矩形OMGN-S△ANO-S△AGB-S△BOM=8
你还有其他方法求△AOB的面积吗?
思考
3.求出如图所示的图形的面积
解:将图形分割成如图所示的三角形
和矩形.
S=S矩形+S三角形=24+12=36
求坐标平面内图形面积:
③分割法,将不规则图形分割成便于计算面积的三角形或四边形。
1. 如何建立平面直角坐标系?
答:选择点作为原点;
过原点在两个互相垂直的方向上分别作出 x 轴和 y 轴;
标出正方向和单位长度.
课堂小结
2. 如何计算坐标平面内图形面积?
方法一:直接法,计算三角形一边的长,并求出该边上的高;
方法二:补形法,将面积转化成若干个特殊的四边形和三角形的面积的和与差;
方法三:分割法,选择一条恰当的直线,将不规则的图形分割成两个便于计算面积的图形.
